圆形人工挖孔桩护壁厚度分析
郭 旭
(福建同力建筑设计院有限公司 福建三明 366000)
0 引言
在土木建筑工程所采用的桩基类型中,人工挖孔桩历史悠久,自20世纪七八十年代桩基础普及开始,人工挖孔桩成桩工艺就作为桩基施工的一种重要方法。由于安全性问题,许多地区近年来已经限制或禁止使用人工挖孔成桩,但由于人工挖孔桩在施工时可直接检查成孔质量,便于观察地质土质变化情况,桩孔深度可由地基土层实际情况加以控制,灵活性和适应性强,施工进度快,方便扩孔以提高单桩承载力,经济性能优越,且桩底清渣干净,易保证混凝土浇筑质量,施工时产生的污染较小,因此在很多工程中人工挖孔桩仍是一种切实有效的成桩工艺并在工程中大量应用。与此同时,近年来人工挖孔桩护壁坍塌导致施工人员伤亡事故也时有发生,归根结底是由于施工设计人员对人工挖孔桩护壁设计和施工技术措施把控的疏忽,若能够从设计及施工技术措施上有效保证护壁安全性能,则人工挖孔桩仍可在我国广大山区土木建筑工程中广泛应用。
1 人工挖孔桩护壁厚度传统计算方法及存在的问题
关于挖孔桩护壁计算,主要问题集中在两个方面,一是土压力q的计算模型,二是护壁的受力机理。
1.1 人工挖孔桩护壁外侧土压力的分析计算主要方法
(1)朗肯土压力理论计算(主动土压力)
对于土质松散,孔隙比较大,基本无内聚力的土体:
γ——土容重;
H——计算点深度;
φ——土壤内摩擦角。
对于有粘性土,由于内聚力在土层产生负侧压力,护壁上部Z0深度不产生侧压力。
粘性土h深度h>Z0处图层主动土侧压力:
q=γHtan2(45°-φ/2)-2ctan(45°-φ/2)
γ——土容重;
H——计算点深度;
φ——土壤内摩擦角;
c——粘聚力标准值。
(2)俄国普洛托齐雅阔诺夫的普式平衡拱理论计算公式[1]
根据散粒体围岩压力的普式理论,土层对护壁的侧压力随着深度增加至一定深度后基本接近于常数,即普式的自然平衡拱理论,当H>(2~3)b1时,侧压力基本为一固定常数:
q=γ1.5b1
b1=a1/fk
a1=R+Htan(45°-φ/2)
H——计算段高度;
fk——岩土坚固系数,砂土取0.6,粉质粘土0.8,粘土1.0,岩石2.0;竖向施工时完全拱效应削弱,故将b1乘1.5系数。
静水压力TwHw,土采用浮容重,桩顶均布荷载折算为填土厚度考虑,填土折算厚度H1=q/R。
(3)前苏联别列赞采夫的筒形地坑壁主动土压力空间问题解析——别式公式[2]:
Rb=R0+Htan(45°-φ/2)
λ=2tanφ·tan(45°-φ/2)
R0——竖井掘进半径。
别式公式从空间考虑了空心圆柱体受力问题,考虑了土体向中心位移时其本身相互挤压使主动土压力减少的有利作用,还考虑了竖井断面大小对主动土压力的影响[3]。综上分析,本文建议在护壁外侧土压力计算时采用别式公式计算较为符合实际情况。
1.2 传统护壁厚度计算的研究常见算法
(1) 材料力学方法计算壁厚[4]:
k——安全系数,取1.65;
q——计算点处土压力;
fc——混凝土轴心抗压强度设计值;
R——掘进半径;
t——护壁厚度。
(2)井圈换算长度法计算壁厚[5]:
Lk——井圈圆环换算长度,取1.82R。
(3) 经验算法壁厚[5]:

D——桩身直径。
(4)在t≥b/10时,采用弹性力学厚壁圆筒模型进行分析[6]:
a——内半径;
b——外半径;
r——计算点处半径。
人工挖孔桩护壁厚度传统计算方法在计算土压力和护壁厚度时,均假设了土体压力为均匀分布,力学模型为圆环截面受均匀土压力作用。计算护壁厚度时仅按混凝土轴心受压进行考虑,未考虑到护壁横截面外侧土质不均匀及开挖过程中孔外土体塌陷、孔外道路车辆行使、地面堆载等因素对井侧壁产生的不均匀土体压力。此外,在实际工程中,混凝土护壁养护时间往往在24h左右就开始继续向下开挖作业,混凝土的早龄期强度远未达到设计值,传统算法中混凝土抗压强度取值明显偏高,对施工安全造成隐患。
2 改进的人工挖孔桩护壁厚度计算方法
鉴于上述传统方法存在的问题,人工挖孔灌注桩护壁厚度计算可按下述方法进行改进。在护壁内力计算时,应充分考虑护壁横截面外侧水平向土压力不均匀分布对内力计算的影响。参照《给排水工程结构设计手册》中沉井横截面水平向土压力分布假设,通过调整孔壁截面两个方向土壤的内摩擦角φ1,2=φ±(2.5°~5°)[7],适当地考虑不均匀土压力。并采用更为符合实际的“别式公式”计算土压力,将护壁计算模型视作受对称不均匀压力作用的封闭圆环进行分析。另外,根据《建筑桩基技术规范》6.6.10条规定,挖孔桩护壁拆模时间应在24h后[8],此时24h龄期时混凝土强度只能达到设计强度约10%~15%[9],拆模强度应达到2.5MPa[10],故在护壁厚度设计计算时,混凝土的抗压强度取值应大幅下调。根据以上分析,建议人工挖孔桩护壁计算按照如下文方法计算。
2.1 考虑土压力分布不均匀,采用“别式公式”计算土压力
在互成90°井圈上两点处沿径向的土压力分别为qA,qB(qB>qA),qA、qB计算时土壤内摩擦角分别采用φ1=φ+(2.5°~5°),φ2=φ-(2.5°~5°), 此时:
Rb1=R+Htan(45°-φ1/2)
λ1=2tanφ1·tan(45°-φ1/2)
Rb2=R+Htan(45°-φ2/2)
λ2=2tanφ2·tan(45°-φ2/2)
护壁横截面外侧土压力分布如图1所示。

图1 护壁横截面外侧土压力分布图
2.2 内力计算
将护壁视作受对称不均匀压力作用的封闭圆环,取1/4圆为计算简图,井圈上任意点土压力按公式变化:
qα=qA(1+ω′sinα)
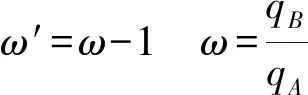
可得:
NA=qAR(1+0.7854ω′)
NB=qAR(1+0.5ω′)
MA=-0.1488qAR2ω′
MB=-0.1366qAR2ω′
护壁横截面弯矩如图2所示。

图2 护壁横截面弯矩图
2.3 壁厚计算
由于护壁拆模时混凝土龄期很短,假设护壁正截面承载能力计算时混凝土应力图形按线性分布,且不考虑混凝土受拉,护壁中的构造钢筋作为安全储备,不参与计算,由材料力学公式推导如下:
假设t<6e,受拉区混凝土开裂,混凝土截面处于大偏压状态,如图3所示。
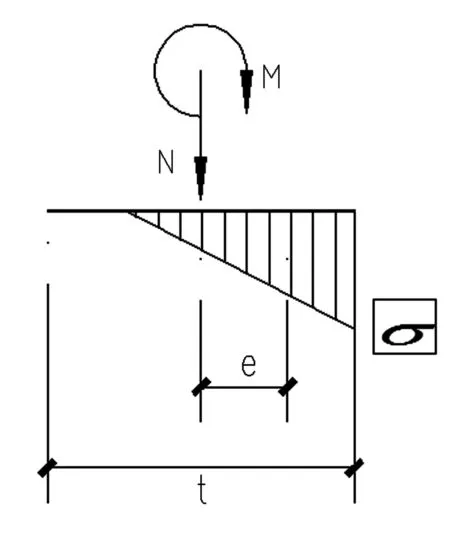
图3 护壁截面大偏心受压混凝土应力图
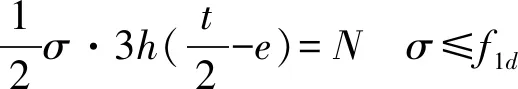
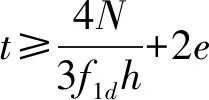
判别,若此时t<6e则上式t即为所求结果。
反之,若t≥6e,截面处于小偏心受压状态,如图4所示。则护壁厚度计算公式如下:
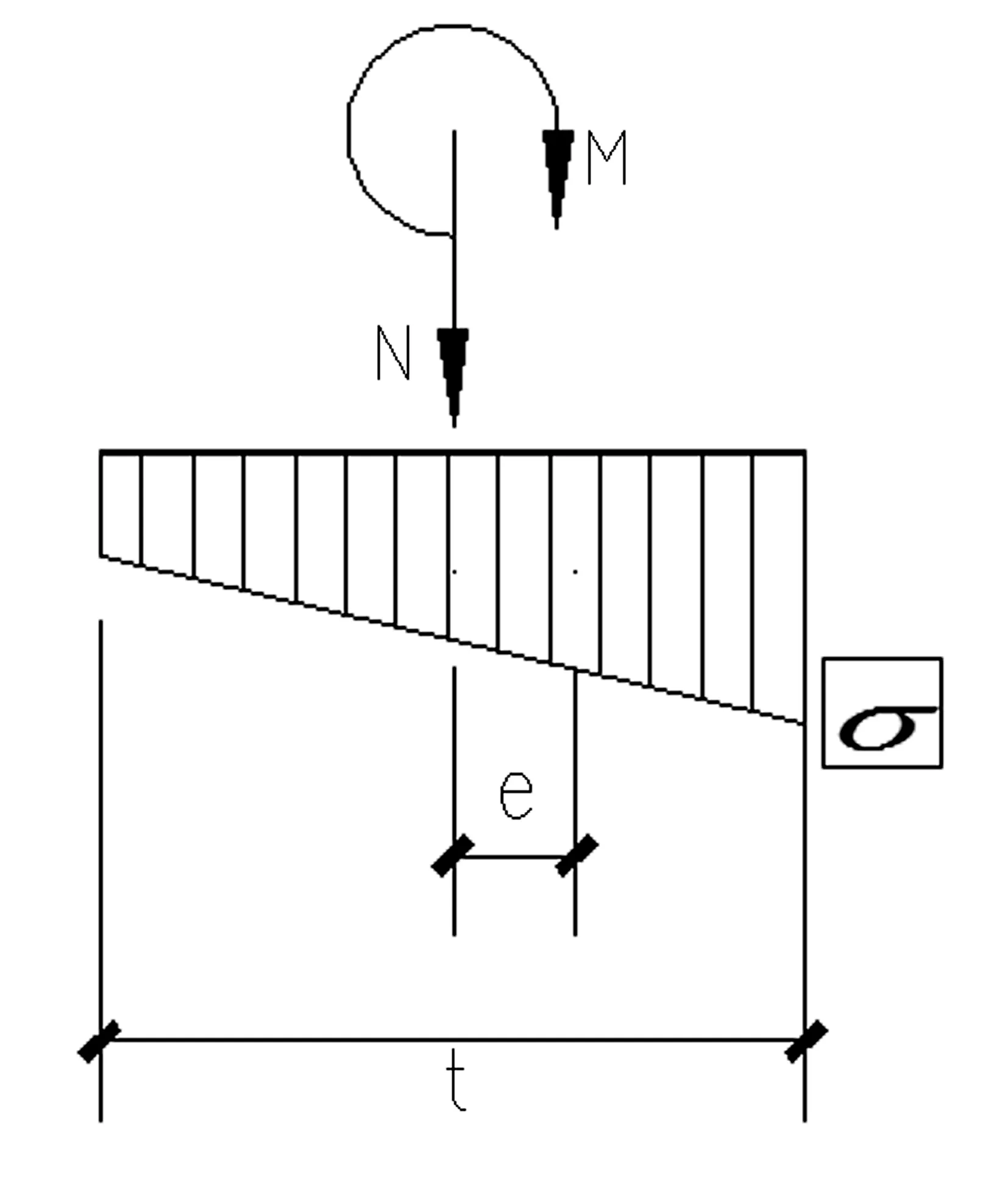
图4 护壁截面小偏心受压混凝土应力图
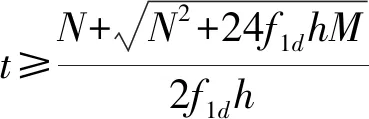
M,N——护壁截面弯矩、轴力设计值,分项系数1.2。分别计算A,B点壁厚取最不利值。
h——每节护壁高度。
f1d——24h龄期混凝土轴心抗压强度设计值,无具体实测强度时,根据模板拆除时混凝土强度须大于2.5MPa,考虑护壁混凝土强度一般较低(≤C40),根据《混凝土结构设计规范(2015版)》4.1.3、4.1.4条[11],此时强度设计值取值约为2.5×0.88×0.76/1.4=1.19MPa。该数值符合在24h龄期,10~20℃温度下,混凝土强度约达到设计值的10%~15%的实验实测结果应注意,若此时能够实测施工时采用的混凝土24h龄期立方体抗压强度,可采用实测抗压强度换算为设计强度进行取值。
3 计算实例分析
设某工程拟采用桩径1600mm人工挖孔桩,桩长15m,无扩底,土体容重均以20kN/m3计、土壤内摩擦角30°,护壁混凝土标号C25,无地下水,取护壁最底部1m计算人工挖孔桩护壁厚度:
R=0.8H=15mγ=20kN/m3φ=30°
fc=11.9N/mm2f1d=1.19N/mm2
取φ1,2=φ±5°⟹φ1=35°,φ2=25°
λ1=2tanφ1·tan(45°-φ1/2)
=2tan35°·tan(45°-35°/2)
=0.729
Rb1=R+Htan(45°-φ1/2)
=0.8+15tan(45°-35°/2)
=8.609m
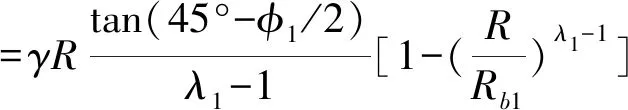
=27.78kN/m
λ2=2tanφ2·tan(45°-φ2/2)
=2tan25°·tan(45°-25°/2)
=0.594
Rb2=R+Htan(45°-φ2/2)
=0.8+15tan(45°-25°/2)
=10.356m
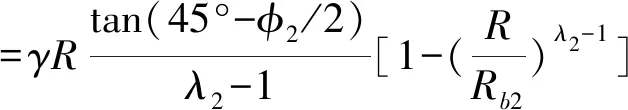
=45.9kN/m
ω′=ω-1=1.652-1=0.652
NA=qAR(1+0.7854ω′)
=27.78×0.8×(1+0.7854×0.652)
=33.6kN
MA=-0.1488qAR2ω′
=-0.1488×27.78×0.82×0.652
=1.725kN·m
NB=qAR(1+0.5ω′)
=27.78×0.8×(1+0.5×0.652)
=29.47kN
MB=0.1366qAR2ω′
=0.1366×27.78×0.82×0.652
=1.583kN·m
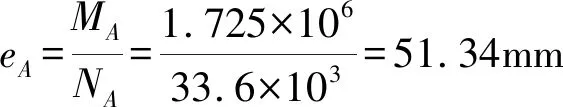
设t<6eA=6×51.34=308mm
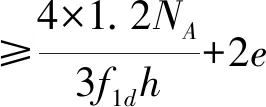
=147.86mm
此时,t<6eA满足要求。

设t<6eB=322.3mm;
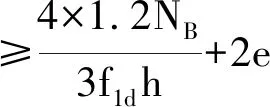
=147.06mm
此时,t<6eB满足要求。
取护壁厚度为150mm,大于《建筑桩基技术规范》最小壁厚100mm要求,构造配筋作为安全储备。
对比传统护壁厚度计算方法:以朗肯土压力和材料力学薄壁圆环应力计算公式计算如下:
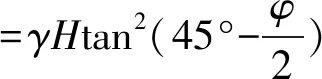
=100kN/m
N=qR=100×0.8=80kN
发现在较大桩径、桩身较长情况下,计算结果仍远远小于护壁构造要求厚度,传统方法得到的计算厚度不具有代表性。
4 结论
在人工挖孔桩护壁厚度计算时,护壁外侧土压力计算采用别式公式,并考虑可能发生的护壁周边土体压力不均匀影响,综合考虑混凝土早龄期强度,推导出切实可行的人工挖孔桩护壁厚度计算方法,能够较好地解决工程施工中的护壁安全性能问题。
——结构相互作用的影响分析

