基于RSSI的室内定位算法研究

宋丽萍

(阜阳职业技术学院，安徽 阜阳 236000)

随着互联网和物联网的迅速发展，物联网的核心技术之一无线传感器网络(Wireless Sensor Networks，WSN)也被广泛应用于各大领域，它是人与自然环境的交互接口，由于 WSN具有体积小、重量轻、功耗少、易实现等特点，所以WSN在恶劣环境条件下也可以正常工作，WSN 具备的优点使一些底层有用的信息可以被随时获取，并广泛应用于智能家居控制、环境监测等领域，WSN的广泛应用将给人们的生活带来不可估量的影响[1].

WSN应用比较广泛的核心技术之一是定位技术，而GPS定位技术因其成本高，信号穿透性差，遇到障碍物无法穿透等各种原因，在室内定位应用中效果不理想.而随着WIFI网络的普及，基于WIFI的室内定位也逐渐被人所关注，WIFI的定位优点是它不需要附加访问接入设备，但由于受环境影响，WIFI的位置性能也不够精确并且具有较高的耗能，因此其应用也受到了限制.如何利用 WSN获取准确的位置信息,实现低功耗、低成本的 WSN 室内定位是人们持续关注的热点之一[2].

1 室内定位算法

根据定位是否有测距的需求，WSN定位算法分为基于测距的定位方法和基于非测距的定位方法.在WSN中，大部分定位主要还是基于距离测量，基于测距的定位算法主要有基于时间到达TOA(Time Of Arrival)、基于时间差TDOA(Time Difference Of Arrival)和基于接收信号强度指示RSSI(Received Signal Strength Indication)的三类定位算法[3].

1.1 TOA

TOA 测距原理主要是通过测量到达时间来测距离，测距分为单向和双向测距技术两种方法，单向测距方法只测量起点到终点的时间，其测距的示意图如图1所示.

这里假设V为传输的速度，T为时间，则距离为S=VT.

而双向测距不但测量起点到终点的到达时间，还要测量终点回到起点的到达时间，其测距的示意图如图2所示.

图1 单向测距方法示意图图2 双向测距方法示意图

这里假设V为传输的速度，T1为到达时间，T2为返回时间，则距离为S=V(T1+T2)/2.

从以上两种测距方法可以看出，TOA测距方法在时间上对同步性的要求较严格.而对于WSN中的节点来说，时间上的同步是很难做到的.

1.2 TDOA

TDOA测距的原理是同一时间向外发射频率不同的两种超声波信号，两种超声波信号的到达时间是不同的，距离是利用两种超声波信号到达的时间差值来计算.其测距示意图如图3所示.

由于超声波信号距离较短，并且在实际环境中还存在着很多影响超声波的障碍物，因此在实际应用中不受欢迎.

1.3 RSSI

RSSI是 Received Signal Strength Indication的缩写，意为接收信号强度，RSSI 测距的原理是通过两节点不同距离时的 RSSI 值建立RSSI距离模型，由得到的 RSSI计算出相应的距离值[4].其测距示意图如图 4所示.

图3 TDOA测距方法示意图图4 RSSI测距方法示意图

基于 RSSI 的测距是一种基于测量距离的无线定位算法，对定位的精度要求不高，而且不需额外的硬件设备，实现简单，通过软件即可实现，成本较低， 因此被广泛应用.

2 基于RSSI的三角形质心定位算法

2.1 三边测量法

假设某一盲节点P和3个锚节点O1、O2、O3，L1、L2、L3为通过接收锚节点发出的信息得到的盲节点P与3个锚节点O1、O2、O3之间的距离，那么分别以锚节点O1、O2、O3为圆心，L1、L2、L3为半径的圆的交点就是盲节点P，如图5所示[5].

2.2 三角形质心定位算法

在实际的定位中，由于噪声的干扰不可避免，因此总是存在测量误差，三个圆不能精确地相交于一个点，而是形成一片区域.此种情况下，通常采用基于 RSSI 的三角形质心定位算法来解决定位，如图6所示.O1(x1,y1)、O2(x2,y2)、O3(x3,y3)为选取的锚节点，P为盲节点，假设O1到盲节点P的距离为L1，O2到盲节点P的距离为L2，O3到盲节点P的距离为L3.根据测距模型，分别以O1、O2、O3为圆心，以L1、L2、L3为半径画圆，三个圆相交形成一片重叠区域[6].

图5 三边测量法图6 三角形质心定位算法模型图

假设A、B、C是三个圆相交形成的重叠区域的三个交点，A(xA,yA)、B(xB,yB)、C(xC,yC)为三个交点的坐标，以A、B、C这三个点为顶点作一三角形，盲节点即为三角形质心P.相交点A的计算方法为：

同理，计算出相交点B和C.此时，可得到盲节点的坐标为：

2．3 质心定位算法

质心定位算法是一种基于网络连通性的定位算法[7].是由Nirupama Bulusu等人提出的，在WSN中，假如在一片区域内分布有n个锚节点，锚节点的坐标为(x1，y1) (x2，y2) …(xi，yi) …(xn，yn) ，则由n个锚节点组成的n-1边的多边形质心(x，y) 为：

在WSN的实际应用中，利用网络连通性，锚节点周期性地向周围分布的节点发送数据包，该数据包中包含锚节点的位置数据，盲节点接连不断的接收数据信息，当接收到一定数量的锚节点信息后，盲节点的位置就是由这些锚节点组成的多边形的质心.由于在传播过程中会发生广播，无线信号会发生变化，另外质心定位算法依赖于锚节点，因此定位精度受锚节点的密度影响很大，质心定位算法的应用并不理想.

3 改进的质心定位算法

由于锚节点的分布影响质心定位算法的精度，所以当监测区域内盲节点周围存在的锚节点极少或因对节点部署不当而导致盲节点无法定位时，将会对定位精度产生很大的影响.针对此种情况，提出一种改进的算法：将已经实现定位的盲节点与锚节点一起周期性地广播数据信息包，这种利用定位过的盲节点实现对未定位的盲节点的定位，可以充分利用WSN中监测区域内的节点，以此提高盲节点的定位精度.该算法流程图如图7所示.

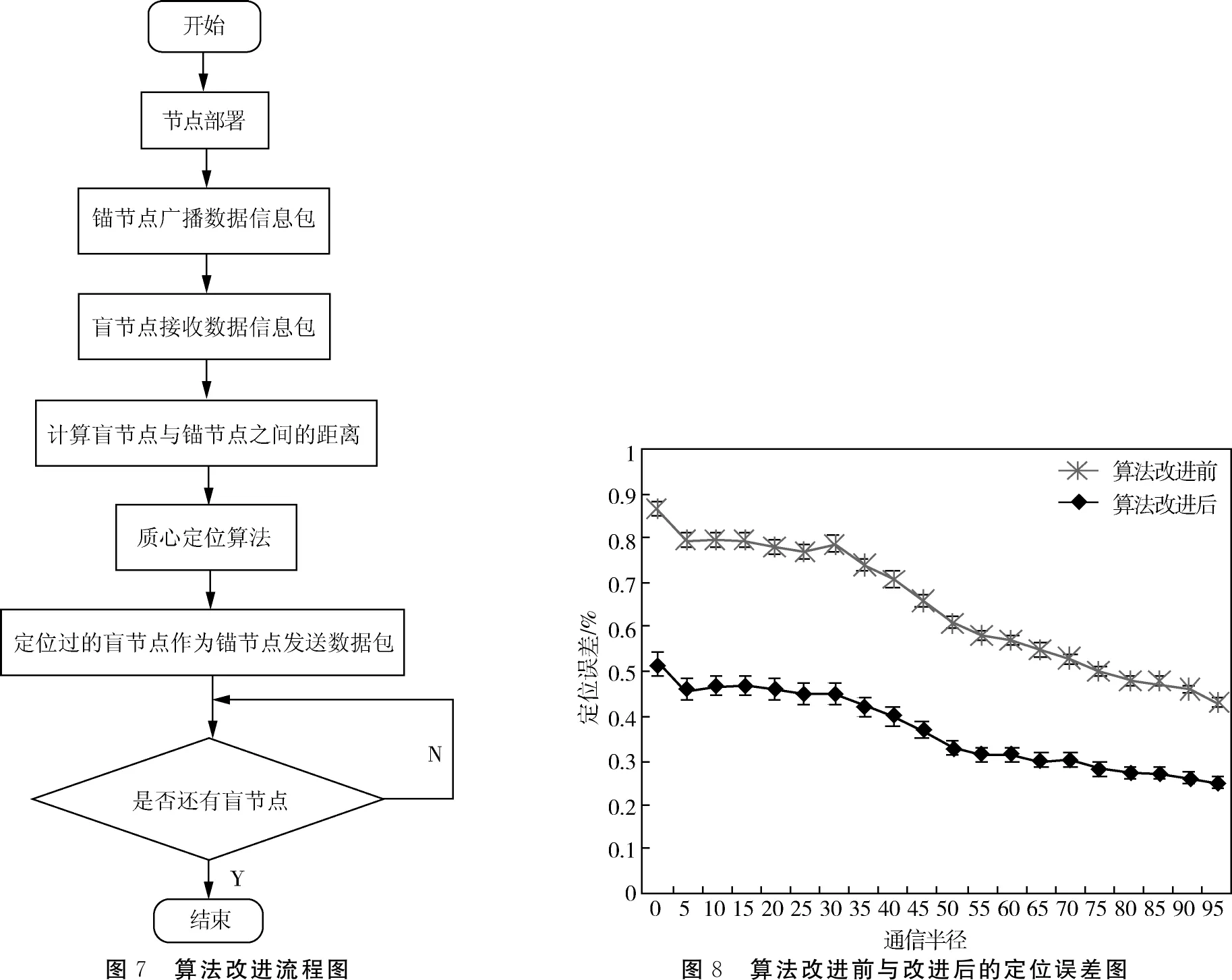
图7 算法改进流程图图8 算法改进前与改进后的定位误差图

4 算法仿真验证

为了比较算法改进前与改进后的效率，进行了仿真实验，实验使用 Matlab软件进行，假设在一片宽为100米的正方形区域内有40个随机分布的盲节点，100个锚节点，在不同通信半径下，对定位算法在改进前与改进后的误差进行比较，仿真结果如图8所示.

实验仿真结果显示，算法改进前后的定位误差随着通信半径的逐步变大而逐步减小，越来越多的节点参与到定位中来，定位的精度也有了一定的提高，在通信半径相同的情况下，算法改进后的定位误差小于算法改进前的定位误差，由此说明，改进后的质心定位算法的定位精度比改进前的质心定位算法的定位精度提高了很多，实现了定位精度的改进效果，算法的改进具有一定的意义[8].

5 小结

随着信息技术的不断发展，WSN的应用已经逐步深入到人们生活的多个领域，与相关的应用越来越多.本文以定位算法为核心，对基于测距的相关的定位技术、定位算法进行了阐述，分析了三边定位算法及普通的质心定位算法，针对其定位的不稳定性和影响定位精度的方面，提出了基于 RSSI 的改进的质心定位算法，对于影响定位精度的因素进行了多方面的考虑与分析，针对通信半径不同的情况下，将算法改进前与改进后两个方面进行对比分析，仿真验证结果表明，算法改进后的定位精度优于传统算法的定位精度.对于 WSN 的探究，本文提出了有关算法的改进和验证，随着应用的不断深入与扩展，会有越来越多的人加入到此领域的研究之中，探究的视角也会越来越宽广.