一种改进地标点采样的不平衡数据聚类算法

韩素青，李淑慧

(太原师范学院 计算机科学与技术系 ,晋中 030619)

0 引言

近年来，随着机器学习的兴起，类别不平衡问题逐渐成为研究的热点.不平衡数据广泛存在于网络入侵检测、软件缺陷检测、医疗诊断等领域[1-3].在不平衡数据中，样本较少的类别通常是关注的焦点.例如，在网络入侵检测中，如果将被恶意攻击的网络误判为正常网络，可能产生信息泄露，由此引发巨大的经济损失.因此对少数类的正确识别至关重要.

聚类分析是一种重要的数据分析技术，是一种以无监督学习方法探索数据的内在结构，进而形成簇的过程.此方法不需要指定样本的类标记，但标记由聚类学习算法自动确定.在聚类分析中，谱聚类是一种利用图划分思想处理数据聚类问题的方法，可以很好地处理非凸结构的数据，并获得令人满意的聚类结果[4-5]，常用于解决数据不平衡的问题.然而，传统的谱聚类算法需要根据数据之间的相似度来构造矩阵，并且还需要拉普拉斯矩阵的特征分解过程.因此，仅适用于小型数据集，而难以处理大规模数据.为提升谱聚类算法的可扩展性，2004年，Fowlkes 等人在文[6]中设计了 Nystrom 方法，并将其用于谱聚类，加快了特征分解的速度.2009年，Yan等人在文[7]中提出一种快速近似谱聚类的思想，即通过选取代表点进行谱聚类，然后再根据数据点与代表点之间的关系将聚类关系扩展到整个数据集上.其中，代表点根据随机抽样产生.2011年，Chen 等人在文[8]中提出一种基于地标点的谱聚类算法(Landmark-based Spectral Clustering， LSC)，并在文[9]中给出了相关的理论分析，结果显示，该方法不仅适用于大规模数据集，而且性能比 Nystrom 方法要好.然而，该方法使用随机采样法来获取地标点，抽样结果会影响聚类结果的稳定性.这容易导致样本点在某一区域的数目很多，而其余区域几乎没有.

本文将LSC算法用于处理不平衡数据聚类问题，提出一种改进地标点采样的不平衡数据聚类算法.该算法根据数据的密度分布对数据进行采样，旨在获得相对平衡的数据集；将在采样数据集上进行K-means聚类获得的聚类中心作为地标点，可以确保算法较大程度地保留数据的主要特征.

1 相关概念

1.1 谱聚类算法原理及主要步骤

谱聚类算法[10]以谱图理论为基础，通过将样本对应于图中的点，样本间的相似度对应于两点间边的权重，将数据的聚类问题转化为图中边的分割问题.

具体地，给定m维的数据集X={x1,x2,…,xn}，首先根据数据点构造相似度图，将求解样本数据集的聚类结果的问题转换为求解图的最小割问题；然后依据图划分准则和谱映射原理，将相似度矩阵变换为Laplacian矩阵.在此基础上，对Laplacian矩阵进行特征分解，也就是将数据转换到一个维数相对较低的特征子空间中；最后在这个子空间中，使用简单的聚类方法对数据进行聚类.

通常，谱聚类算法概括为以下步骤:

Step1 构建数据之间的相似度矩阵Z；

Step2 通过对相似度矩阵进行特征分解，构建特征子空间；

Step3 利用K-means算法或其它有效的聚类算法在特征子空间中对数据进行聚类.

对于任意形状的样本空间，谱聚类算法都能获得良好的聚类效果.但是，处理大规模数据所需的计算量非常大，因此，通过抽样方法获取有价值的数据点来替代原始数据集的方法可减低数据规模，值得进一步探究.

1.2 抽样方法

在处理不平衡数据问题时，重采样是一种常用的采样方法，通过改变训练样本的分布来消除或减小不平衡数据的潜在影响.重抽样通常有两种方法：过采样和欠采样.

过采样通过增加少数类中的样本数来提高模型识别的性能.Ling等人在文[11]中指出，仅通过随机复制少数类样本并不能使样本的识别率提升.Chawla等人在文[12]中提出了SMOTE(Synthetic MinorityOversampling Technique)算法，该算法通过线性插值法在相邻样本之间构造新少数类样本.Han等人则从误分类样本的角度进行分析，认为误分样本一般位于簇类的边界上.因此，只对边界上的少数类样本进行随机复制[13]，但这类方法容易过拟合.

欠采样通过从多数类中删除一些样本来提升模型识别的性能，但是，随机去掉多数类中的某些样本容易导致有用信息被删除的情况发生[14].Jorma在文[15]中提出一种基于最近邻规则的欠采样方法，由于删除了类别边界的多数类样本，因此降低了边界附近数据样本类别的识别效果.Yu等人在文[16]中给出了ACOsampling方法，该方法通过蚁群算法寻找多数类样本中包含最多信息的样本子集，然后将该子集与少数类样本组合成用于训练的新数据集.这类方法的主要缺陷在于有可能丢失包含重要信息的样本子集.Hido等人在文[17]中提出的EBBag算法结合欠抽样和bagging算法设计，对于每次迭代，训练集包括所有少数类样本和从多数类样本中随机抽取的子集，但是，由于抽取的样本是在不考虑数据分布特征的情况下随机选择的，因此很容易丢失有用信息.

目前，大多抽样方法的研究主要基于有标签样本进行，但实际上有许多数据集是无法预先赋予标签的，因此，一些学者也对无类标签的数据的抽样做了一些研究.

Yen和Lee在文[18]中提出一种基于聚类的欠采样方法，该方法是基于预聚类的采样，通过计算样本之间的不平衡度来确定需要保留在聚类中的样本数量，并且根据要保留的样本数随机删除多数类.庞天杰在文[19]中设计的算法采用了先抽取部分样本作为公共样本，然后从剩余样本中多次抽取固定规模的样本，并与公共样本一起形成新的训练样本的策略，聚类结果由多个训练样本集上的谱聚类结果集成.由该策略获得的不同的训样本集，既有一定的差异度，又有一定的相同性.

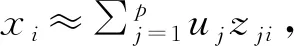
1.3 SVD方法(奇异值分解方法)

本文设计的改进地标点采样的不平衡数据聚类算法，利用奇异值分解(Singular Value Decomposition，SVD)对相似度矩阵进行特征值分解.

SVD是一种常用的矩阵分解(Matrix Decomposition)方法.该方法能够有效获得相似度矩阵的一个低秩近似，降低采样过程的时间复杂度.相关概念介绍如下.

定义1.3.1 设Z∈Cp×n，若ZTZ=ZZT=E,则称Z为酉矩阵.

Z=P∑Q

2 一种改进地标点采样的不平衡数据聚类算法(LSC-SRK算法)

对于地标点的选取，可以采用随机抽样选取地标点或以K-means选取聚类中心为地标点的方法[22].但两种抽样方法处理不平衡数据时存在偏差，少数类样本可能被忽略.因此本文提出先根据样本分布进行抽样然后再进行K-means聚类的SRK(Sample Ratio K-means)方法.

2.1 SRK抽样法

定义2.1 记SampleRatio为簇C的抽样比例，抽样比例计算如下[23]：

其中，R表示簇C的实际半径，EX表示簇C中的各个对象到簇中心的距离的平均值，DX表示簇C内各个对象到簇中心距离的标准差，β为分离不同密度簇的参数.

β的选择方法如下：

1)在簇C内随机抽样产生若干样本点；

2)计算每对样本点之间的欧式距离；

3)计算上述所有距离的平均值μ和方差σ；

4)β取[μ-σ,μ]之间的值.

由于抽样比例函数根据簇的分布特征确定，因此不同分布特征的簇抽样比例不一样.一般来说，簇的密度越大，抽样比例越小，这样能够获得相对平衡的数据集.大量实验表明，β在0.7-1 之间取值能将密度大的簇与密度小的簇较好地分离开.

2.2 LSC-SRK算法

LSC-SRK 算法首先经过预聚类获得数据的初始类标签，其次通过定义2.1的抽样方法获取相对平衡的数据集；数据的相似度矩阵由数据点与地标点之间的相似度矩阵的乘积近似，低维特征空间利用SVD算法获得，聚类在低维特征空间上进行.

LSC-SRK算法流程描述如下：

输入：n个m维数据点形成的数据矩阵X∈Rn×m，簇个数k，地标点个数p；

输出：k个簇；

Step1 对不平衡数据进行K-means预聚类，得到p个簇C(p)={C1,C2,…,Cp}；

Step2 在每个簇中按定义2.1计算类抽样比例SR，并按比例对Ci进行简单随机抽样；

Step3 将每个簇Ci中按比例抽样形成的数据集组合成新的数据子集；

Step4 在新的数据子集上进行二次K-means聚类，并将聚类中心作为地标点，并将p个地标点记为la1,…,lap；

Step5 在地标点和数据点间构造相似度矩阵Z∈Rp×n， 使得

其中，Kh(·)是带宽为h的核函数；

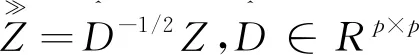
Step7 视矩阵Q的每行为一个数据点并对其进行K-means聚类，得到聚类结果.

Step8 将聚类结果采用最近邻法扩展到整个数据集上.

3 实验与结果分析

3.1 有效性评价指标

本文选取accuracy和CUN两种指标评价LSC-SRK 算法的聚类性能.

假设一个数据集含有n个样本，每个样本具有m个属性，分别为a1,a2,…,am,经过LSC-SRK 算法得到的聚类结果为C(k)={C1,C2,…,Ck}.

(A)accuracy[22]是一种外部评价指标，需要数据的真实划分结果，它用来衡量聚类结果与真实标签之间的吻合程度.

accuracy的表达式如下：

accuracy=∑i=1,…，k(|Ci|/n)

其中，|Ci|是簇Ci中的样本数，k是类数，n是数据集中样本总数.

accuracy的值越高，说明该算法的聚类结果越接近真实划分.

(B)CUN[19]是一种内部评价指标，用来衡量簇内数据点间的紧凑程度.CUN的表达式如下：

3.2 实验数据及实验环境

为了验证有效性，本文从UCI数据集中选取了german,Haberman,balance,abalone,page-blocks 5个不同规模的不平衡数据集进行实验，数据集分布如表1所示.

表1 不平衡数据集

本节基于accuracy和CUN两种评价指标，将本文提出的LSC-SRK算法分别与随机抽样法选取地标点的谱聚类算法LSC-R和以K-means选取聚类中心为地标点的谱聚类算法LSC-K进行了比较和分析.

实验环境为：处理器Intel XeonE5-2680v22 1.8GHz，内存128G，操作系统Windows 7，编程环境MATLAB 2014a.

3.3 实验情况

大量不平衡数据实验[23]表明取β=0.7时能较好地分离密度不同的簇，因此本文实验取参数β=0.7，三种算法各执行5次，并计算其平均accuracy值和CUN值.在不同数据集上的实验结果如表2所示，另外，就数据集的不平衡度对准确性的影响也进行了分析，二者之间的关系如图1所示.

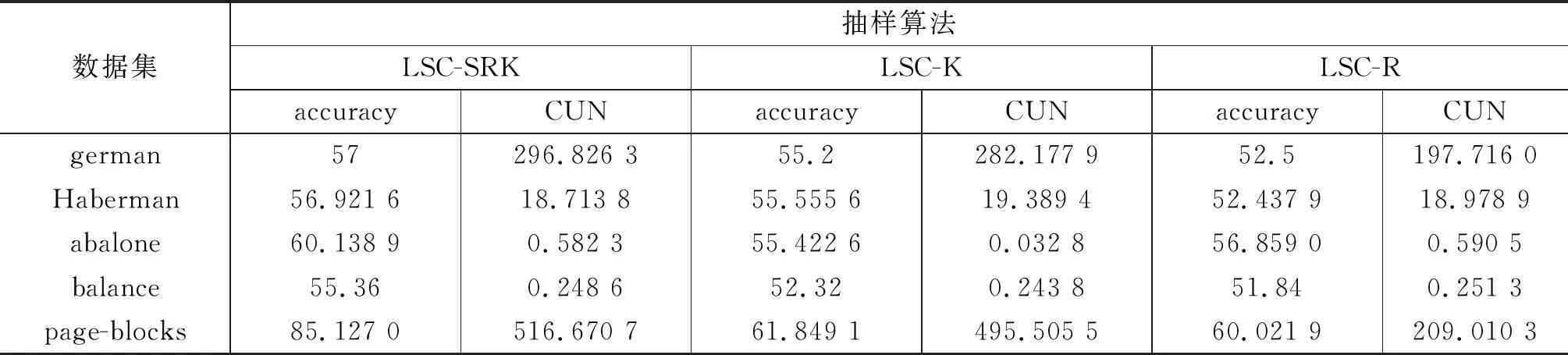
表2 不同抽样方法在聚类算法中的实验结果

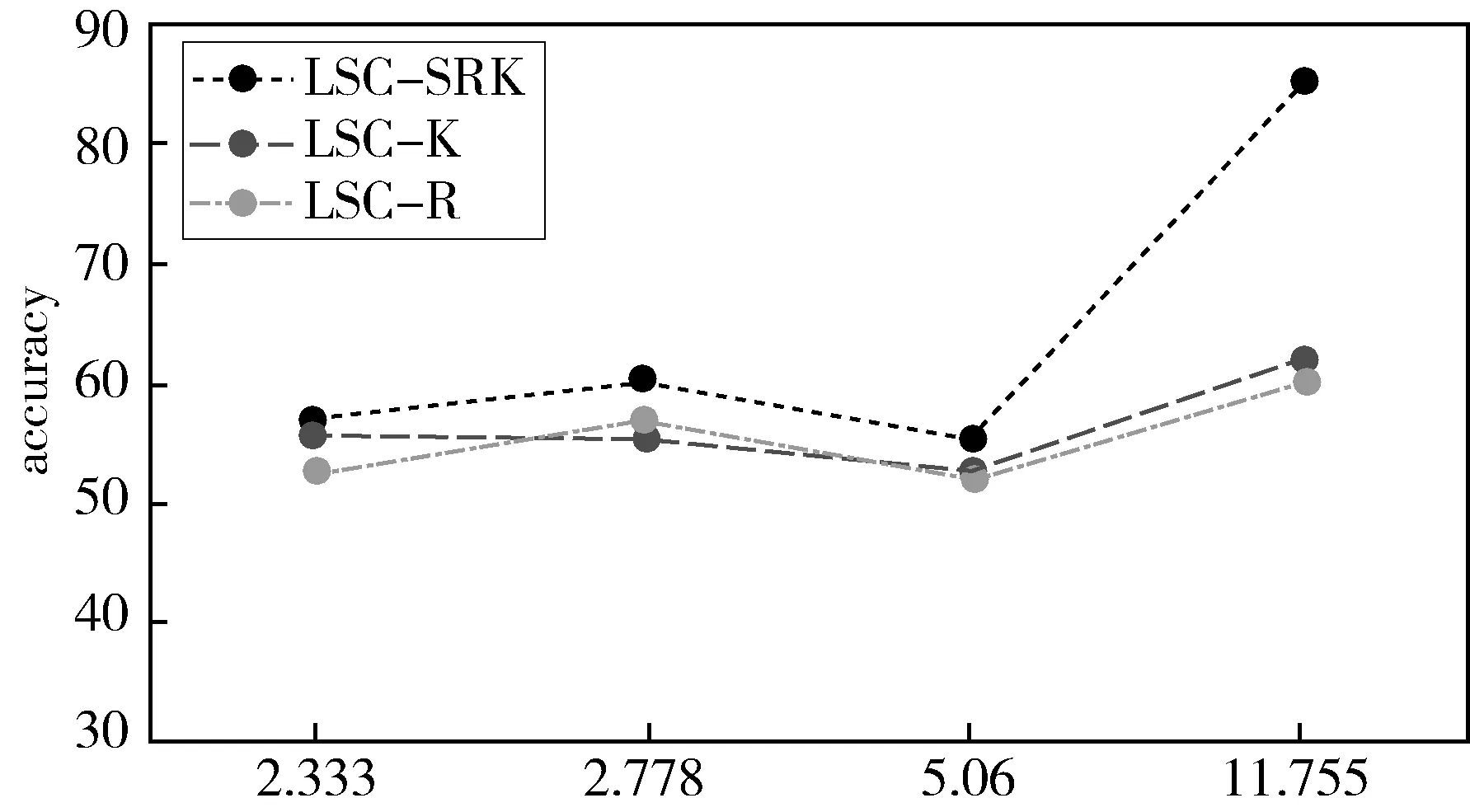
图1 准确度与不平衡度的关系图

从图1可以看出，不平衡度相对较小时，三者算法的准确度差别不大，随着不平衡度的增大，本文提出的LSC-SRK算法与LSC-K、LSC-R相比，准确度明显上升.

从表1，表2可以看出，当数据规模相对较小的时候，LSC-SRK算法的CUN值介于LSC-K与LSC-R之间，数据规模较大时，LSC-SRK的CUN值显著增大，而LSC-K、LSC-R则表现一般.这表明LSC-SRK在大规模数据中能够更有效地区分多数类与少数类，并保证簇内的紧凑程度.由此可以得出，LSC-SRK 算法在实际中更具有意义.

4 结束语

针对不平衡聚类问题中随机抽样选取地标点导致聚类结果不稳定，以及直接将K-means聚类中心作为地标点可能丢失有价值数据等问题，本文改进了地标点采样算法.通过根据数据的密度分布进行采样，以及利用SVD算法快速降维，在算法性能提升的同时，有效节约了谱聚类算法的运算成本.