基于Cobb-Douglas函数的二维网络软件可靠性增长模型
徐雅琴,米晓萍,王金勇,翟新梅
(1.山西卫生健康职业学院(山西省中医学校)信息中心,山西 晋中 030619;2.山西大学 软件学院,太原 030006)
随着万维网和Internet的普及,网站可以为世界各地的用户提供重要的信息服务.由于网络软件要不断满足用户的现实需求,所以要缩短开发周期和减少开发成本,以达到不断更新演化的目的.因此,要保证网络软件的质量和可靠性是一个非常困难的事情[1].到目前为止,网络客户端和服务器呈指数级增长.开放的互联网环境和更广泛的用户群所带来的竞争,也迫切需要解决网络的质量和可靠性问题.
网络应用软件的可靠性可以被定义为应用软件在网络环境下无故障运行的概率.在本文中,定义网络失效为不能够正确获得或者传递信息.例如:网络用户不能够获得请求的文本或者计算结果.这个定义是网络应用软件失效的标准定义,即用户期望的行为偏差[2].
为了增加网络应用软件的可靠性,研究者已经进行了一些相关的研究[1-14].但是,当前存在的方法不能被直接应用到网络系统,因为网络应用软件的特殊本质[1,6],为了能够直接评估网络的可靠性,我们修改了存在的评估网络软件可靠性的方法,并且整合了网络负载特征[7].
网络软件测试是一个复杂的过程,并且评估网络软件可靠性是一个重要的任务.仅仅考虑单因素(如,时间因素)变化来建立网络软件可靠性模型并不符合实际的网络变化需求.因此,建立的软件可靠模型由于没有考虑网络负载变化,他们的合理性受到质疑.
在文中,笔者提出一般的网络软件可靠性模型框架(Framework),即,基于Cobb-Douglas函数的二维软件可靠性模型.我们用Cobb-Douglas函数去整合两个影响网络软件失效的重要因素,即,测试时间和负载.在网络软件测试过程中,考虑网络负载变化更符合实际的网络软件可靠性变化情况.而且,实验结果也证明提出的二维软件可靠性模型和其他模型相比能够在动态变化的网络环境中有更好的拟合和预测性能.
1 网络软件失效数据分析
缩略语:
NHPP 非齐次泊松过程
SRGM 软件可靠性增长模型
TEF 测试工作量函数
LSE 最小二乘法
MLE 最大似然估计
MSE 均值平方误差和
AIC Akaike 信息标注
KD Kolmogorov-Distance
MVF 均值函数
符号说明:
k实际观察到的故障的数量
r威布尔类测试工作量函数的尺度参数
γlogistic测试工作量函数测试工作量消费率
A威布尔类测试工作量常量参数
N最终花费的总的测试工作量
N(t) 到t时刻为止,检测出故障的数量
mi在时间i点,观察到总的失效数量
m(ti) 均值函数,表示到ti时刻为止,期望检测出故障的数量.
W(t) 到t时刻为止,累计检测出测试工作量花费
W*(t)W(t)-W(0)
F(x) 到x时刻为止,期望累计分布
F*(x) 到x时刻为止,观测到标准化的累积分布
网络服务器一般产生两种类型的日志文件,可以把他们作为网络软件失效数据.一类是单个网络访问或者点击数记录在访问日志中.表1[14]列出了一个网站失效的示例条目.另一类是记录在错误日志中的相关问题,表2给出了示例条目说明.

表1 在访问日志中列出的示例条目[14]

表2 在错误日志中列出的示例条目[14]
2 模型开发
2.1 Cobb-Douglas产品函数
Cobb-Douglas产品函数的数学形式被定义为如下形式,
Y=ALνK1-ν.
(1)
其中,Y是每年的总产品量,A是总的产品率因子,L是劳动输入量,K是资本输入量,ν表示为劳动力的弹性系数,是一个固定不变的常量.
从上面的公式(1),能够得出这个函数的基本特征是线性齐次的常量规模收益.例如:所有投入比例的增加导致相同的比例产量增加.因此,Cobb-Douglas产品函数可以被用来整合网络负载和测试时间因子.
2.2 二维网络软件可靠性增长模型
一般来说,为了整合日历时间和网络负载因素,考虑在网络软件可靠性增长过程中同步整合这两个因素的影响.因此,可以用Cobb-Douglas产品函数扩展一维软件可靠性增长模型为下式.
τ=sαu1-α
(2)
其中,τ是测试资源,s是日历时间,u是测试负载因素,α是网络软件可靠性增长过程的影响因子.
网络软件可靠性增长模型可以用数学函数来表示故障检测和去除现象.为了能够在网络环境下应用NHPP模型,给出一些基本假设.
1)在网络运行环境下,故障检测过程服从非齐次泊松分布过程(NHPP).
2)网络软件系统失效是随机发生的,并且是由软件系统中剩余故障造成的.
3)在(τ,τ+Δτ]时间内,检测出故障的数量和系统中剩余故障的数量成正比.
4)每次检测出的故障立即被完全去除,没有新的故障被引进.
假设{N(s,u),s≥0,u≥0}是一个二维随机过程,表示和测试时间s和测试负载u相关的累积检测出软件失效的数量.一个具有均值函数m(s,u)的二维非齐次泊松过程可以被定义为,
(3)
k=0,1,2,…
(4)
其中λ(ζ,ξ)表示双变量故障强度函数.一般NHPP模型假设软件失效和软件中剩余故障有关.在由假设3,建立如下相关的微分方程,
(5)
其中,a表示期望最初检查出故障的数量,b(τ)表示双变量故障检测率函数,为简化计算,一般假设为常量.
Case 1:
如果b(x)=b,那么求解方程(5),双变量均值函数可以表示为,
m(τ)=a[1-exp(-bτ)].
(6)
Case 2:
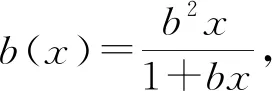
m(τ)=a[1-(1+bτ)exp(-bτ)].
(7)
Case 3:
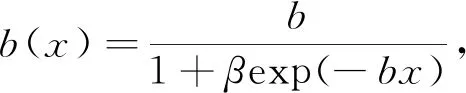
(8)
表3详细列出本文中提出的二维网络软件可靠性模型和其它网络软件可靠性模型.在表3中,TDG-O模型、TDDSS模型和TDISS模型分别表示为二维G-O模型(TDG-O),二维Delayed S-shaped模型(TDDSS)和二维Inflection S-shaped 模型(TDISS).
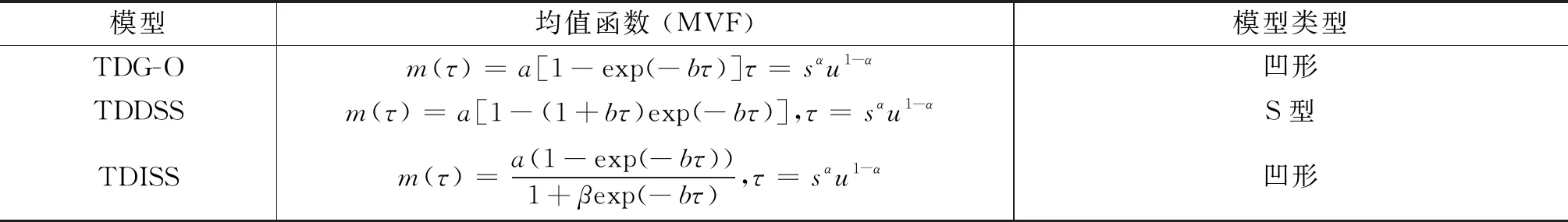
表3 本文使用的网络软件可靠性模型和它的均值函数总结
3 数值例子
在本文中,来用提出的模型去评估两个网站的可靠性.第一个网站是ICRMS网站,它的网址是www.icrms.cn.第二个网站是一个官方网站(SMU/SEAS),它的网址是www.seas.smu.edu[8].为了量化比较的结果,用三个模型比较标准.为了验证提出的二维软件可靠性模型的性能,用两个故障数据集表4、表5进行了相应的拟合和参数估计以及预测结果比较.
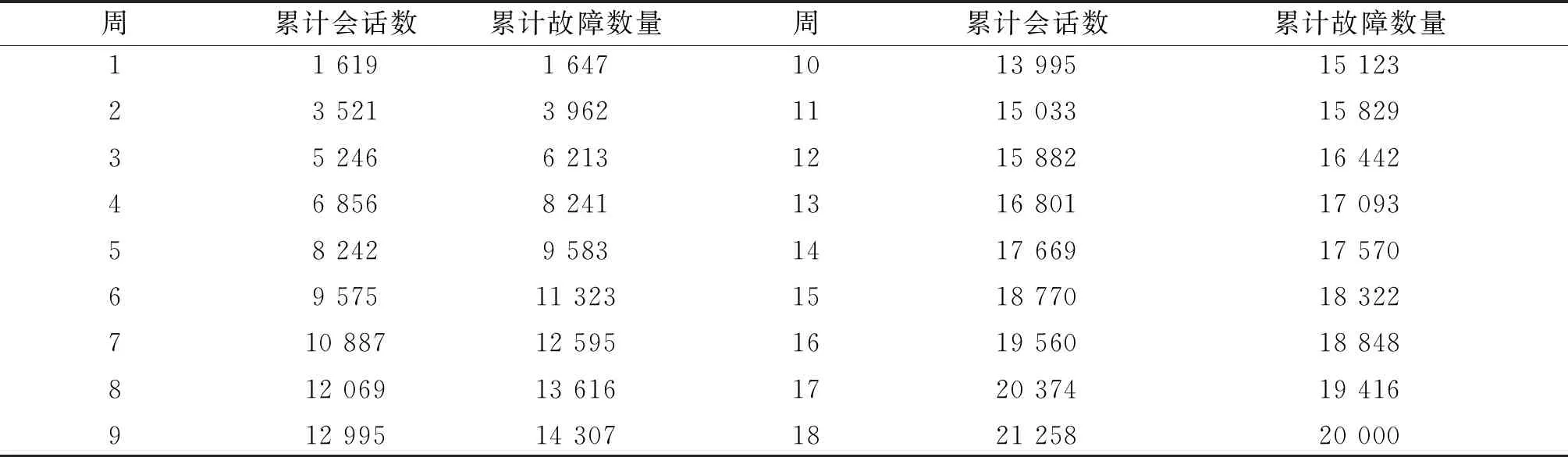
表4 故障数据集1(DS1)

表5 故障数据集 2(DS2)
3.1 模型的参数估计方法
为了得出无偏差的结果,分别用来用最小二乘法(LSE)和最大似然估计方法(MLE)来估计模型的参数值.
假设有k个数据对(si,ui,yi) (i= 0,1,2,…,k;s0 (9) (10) 可以分别得出参数a,b,β和α的值. 另一方面,参数值可以用最大似然估计方法进行估计.从公式(3),我们能够得出 Pr{N(si,ui)=ki,i=1,2,3…}= (11) 因此,最大似然估计函数可以表示为, (12) 那么公式(12)两边取对数可以得到下式, l=logL. (13) 因此,模型的参数可以用下式估计出来, (14) 3.2.1 模型拟合性能比较 从表6可知,TDISS模型在用故障数据集1进行100%的故障数据拟合和LSE方法参数估计时的MSE和KD值都小于TDG-O,TDDSS和测试工作量模型.显示TDDSS模型的MSE和KD的拟合值都大于TDG-O和TDISS模型.同类,从表6可以看到,当用DS1和DS2的100%的故障数据拟合和用MLE方法估计模型参数时,TDG-O模型的AIC和KD的拟合值与TDISS模型的近似相等.并且TDG-O模型和TDISS模型的AIC和KD的拟合值要小于TDDSS模型和测试工作量模型.因此,TDDSS的拟合能力比TDG-O模型和TDISS模型都要差. 表6 用DS1和DS2的100%的故障数据集进行软件可靠性模型比较结果 从上面的分析能够得出,文中提出的二维软件可靠性模型有很好的拟合性能.对不同的二维软件可靠性模型进行比较发现,TDG-O模型和TDISS模型与TDDSS模型和测试工作量模型相比有更好的拟合性能. 3.2.2 模型预测性能比较 从表7知,用DS1的60%的故障数据时,无论是用LSE还是MLE估计模型的参数,TDISS模型拟合的MSE和KD的值都小于TDG-O模型和TDDSS模型.但是,在用DS1的60%的故障数据时,无论是用LSE还是MLE估计模型的参数,TDG-O模型预测的MSE和KD的值都小于TDDSS模型,TDISS模型和测试工作量模型.而TDDSS模型的拟合和预测性能与TDG-O模型和TDISS模型相比是最差的.对于AIC值,TDG-O模型和TDISS模型相差不大,它们都小于TDDSS模型. 表7 用故障数据集1的60%故障数据进行软件可靠性模型比较的结果 同类,从表8得出,在用DS2的60%的故障数据和用LSE估计模型的参数时,TDISS模型的拟合和预测的MSE值都小于TDG-O模型和TDDSS模型.但是,在用DS2的60%的故障数据和用LSE估计模型的参数时,TDG-O模型拟合和预测的KD值都小于TDDSS模型和TDISS模型.另外,从表8,我们还能看到在用DS2的60%的故障数据和用MLE估计模型的参数时,TDISS模型拟合的MSE和KD值都小于TDG-O模型和TDDSS模型.但是,在用DS2的60%的故障数据和用MLE估计模型的参数时,TDG-O模型预测的MSE和KD值都小于TDISS模型,TDDSS模型和测试工作量模型.其中,在用DS2故障数据集和LSE与MLE估计模型参数时,TDDSS模型在三个提出的二维软件可靠性模型中的拟合和预测性能都是最差的.TDG-O模型的AIC值和TDISS模型的AIC值近似相等.他们都小于TDDSS模型. 表8 用故障数据集2的60%故障数据估计软件可靠性模型参数值 总的来说,可以合理地得出TDG-O模型和TDISS模型有更好的拟合和预测性能.在用Cobb-Douglas产品函数来整合测试时间和网络负载后可以更有效地评估网络软件的可靠性.而且,提出的二维软件可靠模型在拟合和预测软件中剩余故障的数量时都有较好的性能.因此,文中提出的二维软件可靠性模型可以被应用到实际的网络软件可靠性评测中. 从网络软件实际失效发生机制的角度来看,网络软件可靠性增长过程不但依赖时间因素,而且还与网络负载有关.例如:点击数,位数,用户数和会话数等.在本文中,开发了一个整合了测试时间和网络负载的二维网络软件可靠性增长模型,并且用ICRMS和SMU/SEAS 网站的服务器的日志中收集的两个故障数据集验证了提出的二维软件可靠性模型的拟合与预测性能.基于AIC,MSE和KD比较,提出的二维网络软件可靠性模型在动态的网站测试中有更好的拟合和预测性能,并且能够准确地预测软件中剩余故障的数量.实验结果也指出提出的二维TDG-O和TDISS模型在所有模型中有更好的拟合和预测性能.
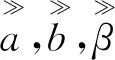
3.2 模型性能分析和讨论



4 结束语

