直流多馈入系统有效广义短路比

徐 谦，戴 攀，章 枫，辛焕海

（1.国网浙江省电力有限公司经济技术研究院，杭州 310008；2.浙江大学电气工程学院，杭州 310027）

0 引言

近些年来，随着电网LCC-HVDC（相控换流高压直流输电）技术的快速发展，多回直流落点于同一交流受端电网的MIDC（直流多馈入系统）已经在我国三华及南方电网中形成[1-3]。

直流多馈入系统在规划、设计和运行中较直流单馈入系统更难分析，其电压稳定性问题尤为突出[4-5]。目前，针对直流多馈入系统的电压稳定性通常使用受端交流电网的强度来衡量[4]，国内外学者对其具体强度衡量问题进行了大量研究并提出了多种强度评价指标：CIGRE 提出的MISCR（多馈入短路比）指标[4]；MISCR 的改良指标[3，6-11]；MISCR（多馈入综合短路比）指标[12-13]等。上述工作虽解决了直流多馈入系统强度评价指标的缺失问题，但是其物理意义不清晰，强度区分边界值不准确[9-10]。因此，基于模态分析法[14-15]且类比单馈入短路比，文献[16-17]提出了一种新的gSCR（广义短路比）指标。该指标虽然克服了传统多馈入指标物理意义不明确及边界刻画不准确的缺陷，但其推导需基于若干假设条件，如线路为纯电抗，直流无功功率需就地近似由无功补偿电容完全补偿等。在实际电力系统中，这些假设条件过于苛刻，当假设条件弱化后，广义短路比的适应性问题目前尚缺乏深入的研究。

为此，本文探索了弱化假设条件后广义短路比的适用性问题，具体体现为，本文分析了无功补偿电容对于广义短路比的影响，基于有效短路比指标提出了一种考虑无功补偿的广义短路比指标EgSCR（有效广义短路比），克服了广义短路比推导过程中需假设直流消耗无功近似完全补偿，无功补偿容量与直流系统额定容量成比例的缺陷。理论分析和仿真算例均表明新定义下的有效广义短路比更具普适性，能更准确地描述考虑无功补偿电容的直流多馈入系统受端交流电网强度。

1 直流单馈入系统有效短路比

在直流单馈入系统中，为补偿直流从交流电网吸收的无功功率，在直流整流和逆变侧的交流母线处常并联电容器及滤波器等无功补偿设备。无功补偿设备的存在提升了交流系统的短路容量，故为去除其对于系统短路比的影响定义单馈入有效短路比[4]：

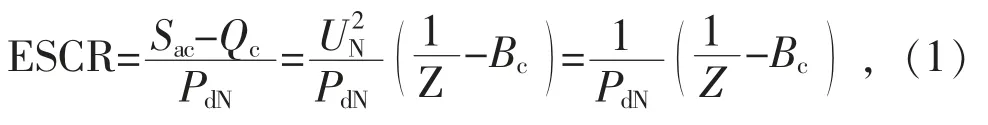
式中：Sac为交流短路容量；Qc为无功补偿容量；PdN为额定直流输送功率；UN为直流馈入点交流额定电压；Z 为交流系统等效电抗（忽略线路电阻）；Bc为无功补偿电容。

在直流典型参数下，常分别用CESCR（临界有效短路比）和BESCR（边界短路比）区分极弱、弱系统和弱、强系统，通常CESCR≈1.5，BESCR≈2.5。

2 直流多馈入系统雅克比矩阵

考虑存在n 条直流线路馈入受端交流系统，如图1 所示，且系统满足如下2 个假设条件：考虑n 条直流系统都是相似的，即除了额定容量外，以自身容量为基准的主电路参数标幺值都相同，直流间联络线功率远小于其传输极限；受端交流系统是电感型（不考虑线路电阻）、拓扑连通的系统（即导纳矩阵可逆且对称）。

图1 多馈入交直流系统

2.1 直流系统雅克比矩阵

此时，直流多馈入系统的潮流雅克比阵为：

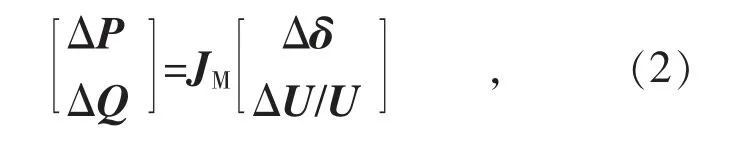
其中：

式中：ΔP 和ΔQ 分别为逆变侧换流母线有功和无功功率的摄动值；Δδ 和ΔU/U 分别为逆变侧换流母线相角摄动值和电压百分比摄动值；H，N，J，L 分别为多馈入系统中交流雅克比矩阵元素；分别为多馈入系统中直流雅克比矩阵元素。

由于直流系统有功和无功功率与逆变站交流母线相角相关性很小，有功功率与交流母线电压相关性也很小，均可忽略不计。类似于文献[16]，可知为一个对角矩阵，为零矩阵：

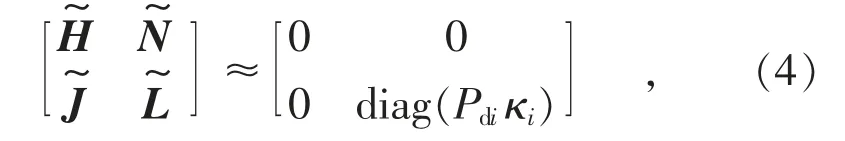
式中：Pdi为直流输送的有功功率；κi（·）=2ciKi；i表示参数为第i 条直流参数；diag（ai）表示对角矩阵diag（a1，a2，…，an）；ci和Ki的表达式同文献[16]。

2.2 交流系统雅克比矩阵

由于直流第i 个节点处的功率平衡方程为：

式中：Pdi为第i 条直流注入交流电网有功功率；Qdi为第i 条直流注入交流电网无功功率；δij=δi-δj为第i 条直流和第j 条直流的母线电压相角差；Bij为系统导纳矩阵B 的元素；Bci为第i 条直流逆变侧无功补偿电容；Ui为第i 条直流换流母线电压幅值。

由式（5）可以求得式（3）中交流雅克比矩阵各元素的表达式分别为：

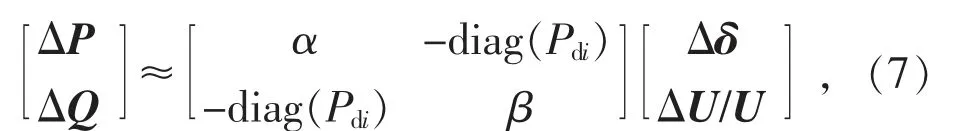
3 多馈入系统有效广义短路比

结合式（4）和（7）可知式（3）中JM为：

类似于直流单馈入系统，在直流多馈入系统中，当系统到达静态电压稳定极限时，系统潮流雅克比矩阵奇异[20]，此时雅克比矩阵JM的行列式等于零，即：

根据矩阵Schur 变换，式（9）与下式等价：

其中：

式（10）可改写为：

式中：D=diag-1（PNi）。

（1）针对图1 所示的直流多馈入系统，在假设1 成立的情况下，直流运行工况发生变化时，只要多馈入系统中所有直流的换相重叠角和熄弧角始终保持一致，则tanφi=tanφj对所有的i 和j都成立。

（2）针对图1 所示的直流多馈入系统，在假设2 成立的情况下，矩阵的特征根均为正实数，其最小特征根是个简单的特征根，且对应的特征向量所有元素都为正[16]。

由文献[16]可知，直流运行工况发生变化时，只要多馈入系统中所有直流的换相重叠角和熄弧角始终保持一致，则所有直流ci，κi和ρi也分别相同，将式进行特征值分解后化简为：

当直流多馈入系统逐步接近静态电压稳定极限点时，式（14）中的特征值逐渐减小直至满足式（14）的情况，即雅克比矩阵奇异，由于矩阵特征值的特殊性，其最小特征值总是先满足式（14）的等式，故最小特征值表征的系统稳定裕度与式（14）等价，即Δ（O）=ρκ-λ1-ρtanφ+ρ2（λ1-ρtanφ）-1代表了整个多馈入直流系统的电压稳定裕度。

参考广义短路比的概念，可以将功率权重下计及无功补偿电容及滤波器对地支路的导纳矩阵的最小特征值λ1定义为EgSCR。

（1）计及无功补偿电容及滤波器对地支路的功率权重导纳矩阵的最小特征值，称为多馈入有效广义短路比，即：

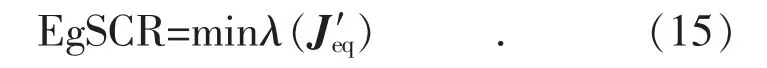
结合式（14）和（15）可以看出，直流系统的运行工况同有效广义短路比一起组成了直流多馈入系统静态电压稳定判据表达式，式（14）是系统发生静态电压稳定的近似充要条件，说明EgSCR与电压稳定存在直接的联系。

4 仿真分析

为了方便起见，本文分析所采用的直流系统均为CIGRE 工作组在1991 年提出的标准模型，且不考虑LCL 滤波器仅考虑无功补偿电容。

4.1 单馈入临界和边界有效短路比

本小节在MATLAB 软件上进行仿真计算，以验证在典型参数下，单馈入临界有效短路比约为1.527，单馈入边界有效短路比为2.377。

首先验证单馈入临界有效短路比。考虑一个直流单馈入系统，改变无功补偿电容Bc的值，令其从0.2 p.u.连续变化到1.3 p.u.，对应实际直流单馈入系统无功补偿由欠补偿到过补偿的过程。根据式（1）的有效短路比定义，在无功补偿电容变化的过程中，改变戴维南等值电抗，令ESCR 维持在1.527。为保证直流单馈入系统在额定工作点处，逆变站交流母线电压幅值仍为1 p.u.，变化过程中，需改变戴维南等值电势，其计算公式为

计算直流单馈入系统在有效短路比均为1.527，但无功补偿电容不同的情况下，直流传输的直流功率及逆变站交流母线电压随着直流电流增长的变化曲线；同时计算不同无功补偿电容下，戴维南等效电势值随着无功补偿电容增长的变化曲线，结果如图2 所示。

图2 功率、交流电压及戴维南等效电势曲线

从图2 可以看出，系统的最大功率曲线、逆变侧交流母线处电压随直流电流的变化曲线与无功补偿电容Bc值无关，只与系统有效短路比值相关。当有效短路比为1.527 时，不管无功补偿电容如何变化，直流系统的最大功率点和额定点重合，即在CIGRE 的典型直流模型下，临界有效短路比为1.527。此临界值可用于严格区分直流系统在额定点处的稳定性：若有效短路比小于1.527，系统被称为极弱系统；若有效短路比大于1.527，系统被称为弱系统。

同理考虑一个直流单馈入系统，其中无功补偿电容Bc仍由0.2 p.u.连续变化到1.3 p.u.，对应实际直流单馈入系统无功补偿由欠补偿到过补偿的过程。在无功补偿电容变化的过程中，改变戴维南等值电抗，令ESCR 维持在2.377。为保证直流单馈入系统在额定工作点处，逆变站交流母线电压幅值仍为1 p.u.，变化过程中，需改变戴维南等值电势，其计算公式为

计算此时直流单馈入系统在有效短路比均为2.377，但无功补偿电容不同情况下，直流传输的直流功率、逆变站交流母线电压及换相重叠角随着直流电流增长的变化曲线；同时计算不同无功补偿电容下，戴维南等效电势值随着无功补偿电容增长的变化曲线，结果如图3 所示。

图3 功率、交流电压、换相重叠角及戴维南电势曲线

从图3 可以看出，系统的最大功率曲线、逆变侧交流母线处电压及换相重叠角随直流电流的变化曲线与无功补偿电容Bc值无关，只与系统有效短路比值相关。 当有效短路比为2.377 时，直流系统的最大功率点和换相重叠角μ=30°工作点重合，即在CIGRE 的典型直流模型下，边界有效短路比为2.377。此边界值可用于严格区分直流系统在换相重叠角μ=30°工作点处的稳定性：若有效短路比大于2.377，系统被称为强系统。同时从图中还可以看出，随着无功补偿电容的增大，戴维南等效电势将随之减小。为了降低系统的过电压水平，一般令无功补偿电容完全或过补偿直流吸收的无功功率。

4.2 多馈入临界和边界有效广义短路比

为了进一步说明多馈入临界和边界有效广义短路比值分别为1.527 和2.377 的性质，下面基于CIGRE 的标准直流模型构造如图1 所示的直流多馈入系统。在此基础上，改变系统的交流侧网络参数（戴维南等值阻抗），使得系统有效广义短路比值分别满足EgSCR=1.527 和EgSCR=2.377，并观察临界运行点的特性：当EgSCR=1.527 时，极限功率点是否为额定运行点；当EgSCR=2.377时，增加直流功率使得系统到达极限工作点，此时直流换相重叠角是否为30°。

共使用6 个直流多馈入算例，各算例的网络参数如表1 所示。在DIgSILENT 软件中按表1 参数搭建直流多馈入系统，并以潮流不收敛为静态电压稳定判据，计算求得静态电压稳定极限点处的运行工况，结果如表2 所示。

表1 多馈入等值网络参数

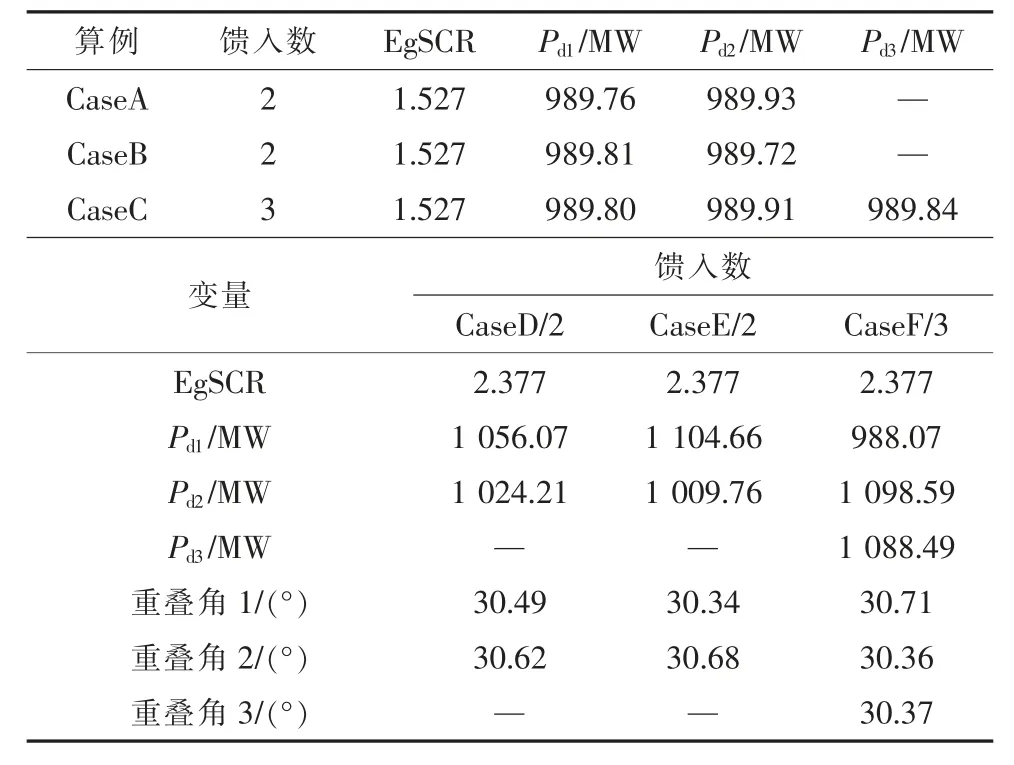
表2 静态电压临界点运行工况

由表2 的CaseA，CaseB 和CaseC 可以看出，在EgSCR=1.527 时， 不管系统的无功补偿如何（CaseA 直流1 和2 均欠补偿；CaseB 直流1 欠补偿，直流2 过补偿；CaseC 直流1 和2 欠补偿，直流3 过补偿），系统的极限馈入功率和额定功率差别很小，故可以认为在额定运行点，多馈入系统的临界有效广义短路比与1.527 偏差很小。因此，工程上可以使用EgSCR=1.527 来近似区分极弱和弱交流系统，并且带来的功率最大值偏差小于0.03%。

类似地，由表2 的CaseD，CaseE 和CaseF可以看出，在EgSCR=2.377 时，不管系统的无功补偿如何（CaseD 直流1 和2 均欠补偿；CaseE 直流1 欠补偿，直流2 过补偿；CaseF 直流1 过补偿，直流2 和3 欠补偿），系统到达静态电压临界点时，所有直流均运行在换相重叠角μ=30°附近，最大误差不超过1°。故可以认为，多馈入系统的边界有效短路比与2.377 偏差很小。因此，工程上可以使用EgSCR=2.377 来近似区分弱和强交流系统。

5 结论

（1）无功补偿电容会影响直流多馈入系统的静态电压稳定，即影响广义短路比指标。若无功补偿电容的容量不等于完全补偿直流从交流系统吸收的无功容量，广义短路比指标将不再适用。

（2）考虑无功补偿电容对直流多馈入系统静态电压稳定的影响时，可定义有效广义短路比，有效广义短路比是广义短路比的修正。理论分析和算例均说明，有效广义短路比指标能够用来区分受端交流系统的强弱，即如果有效广义短路比小于1.527，则受端系统为极弱网；若有效广义短路比大于2.377，则受端系统为强网；若有效广义短路比介于1.527 和2.377 之间，则受端系统为弱网。