基于虚拟电流注入技术的有源配电网故障定位

梁梦可，刘 远，韩文文，高 晗，李意欣

（国网河南省电力公司新乡供电公司，河南 新乡 453000）

0 引言

有源配电网在发生短路故障时，能够自动识别和隔离故障区域，快速恢复对非故障区域的供电，达到减小停电区域和缩短停电时间的目的。若不能快速确定故障发生区域以及故障发生点，将会导致故障事故进一步扩大，影响整个电网的安全稳定运行。因此，国内外研究人员对故障区域的识别和判断进行了大量研究。

在配电自动化系统中，FA（馈线自动化）是基于自动重合装置[1-3]、故障指示器[4-5]等装置的故障区域识别技术，目前已经十分成熟。随着FTU（配电开关监控终端）在配电网中的大量安装使用，基于FTU 的故障区域定位算法已经做了大量研究，可分为矩阵算法、人工智能算法和其他算法。

传统矩阵算法是一个N×N 阶稀疏方阵，随着节点数的增加，势必面临存储和编程会占据大量存储空间，故障判断的实时性将会降低[6-7]；文献[8]将HEA（人类进化算法）应用于配电网故障区域识别，但是需要采集大量的节点过电流信息，针对有源配电网的发展缺乏考虑，存在明显不足；文献[9]将粗糙集理论和免疫算法相结合来挖掘配电网故障数据，从而形成故障识别相关性模型，需要构造故障模型数据库，简化成最佳属性条件下的决策规则数据库，通过比较分析故障越线信息即可识别故障区域，但是算法灵活性较差，当配电网拓扑结构发生变化时，需要重新建立故障模型数据库。

本文采用的故障定位算法基于注入虚拟电流技术，无需附加设备；而且针对配电网存在线路参数不对称以及负荷不平衡等特性，运用改进后的三相前推回代算法，通过添加收敛因子来克服故障配电网不收敛的特性。通过在PSCAD 上搭建有源配电网的仿真模型，利用MATLAB 进行数据分析和算法验算，验证了所采用故障定位算法的准确性和有效性。

1 分布式电源的模型分析

随机波动的DG（分布式电源）并网运行使有源配电网的结构更加复杂，DG 因自然条件的影响而具有波动性，出力具有时变性，而且DG 参数（电动势和次暂态电抗）、故障类型和过渡电阻等具有不可知性，这些具有不确定性的未知参数和变量对故障定位的可靠性和准确性具有重要影响。DG 的数学模型直接影响有源配电网故障定位的可行性和准确性。

1.1 DG 等效模型

针对不同种类的DG 可采取等效戴维南模型，如图1 所示，通过采用对称分量法将光伏、风力、燃气轮机发电和燃料电池分解成正序、负序和零序模型。有源配电网中，根据DG 生产厂商所提供的参数数据建立的DG 等效模型，其系统阻抗与电压源串联的模型不能精确反映DG 故障特性，将给故障定位带来较大误差。本文采用的方法是利用DG 端口的电压和电流，进而确定其戴维南等效模型的简单阻抗法。

图1 戴维南等效DG 模型

1.2 等效模型的推导过程

DG 主要包括光伏发电、风力发电、燃气轮机和燃料电池，在文献[10-11]中等效为理想电压源与等效阻抗串联的等值电路。假定在DG 接入配电网正常运行状况下，DG 只有正序电压和正序电流注入配电网；在故障状态下，等效模型会出现零序和负序分量。

采取理想电压源串联阻抗矩阵来模拟DG 接入配电网运行，通过端口电压值和电流值来计算其戴维南等效阻抗值。 当DG 接入配电网运行时，图1 中其等效模型可解耦成正序、负序和零序网络。其故障前的计算式为：

故障情况下的正序阻抗计算为：

根据式（1）和式（2）可求得正序阻抗为：

其中：

同理，其负序和零序阻抗为：

通过布置在DG 馈线接入点的RTU 测得正常运行状态下的端口电压UL和电流IL、故障状况下的电压UF和电流IF。通过对称变量法对电压进行相模变换，可得到端口电压和电流的正序、负序、零序分量，如式（6），（7）所示，进而求得DG 系统阻抗的正序、负序和零序阻抗。

式中：变换因子a=ej2π/3；S 是对称分量变换矩阵；T 表示矩阵转置；S-1表示矩阵S 的可逆矩阵。

根据DG 的序阻抗，可进一步将DG 的戴维南等效序阻抗矩阵转换为耦合的三相阻抗矩阵Zabc，可采用对称分量法的逆运算[12]，其计算过程如式（8）所示。

式中：Z012是序阻抗矩阵；Zaa，Zbb和Zcc是DG 各相的自阻抗；Zab，Zac，Zbc，Zba，Zca和Zcb是各相之间的互阻抗，其中矩阵Zab=Zba，Zac=Zca和Zbc=Zcb。

通过以上推导，针对三相对称的DG 可利用故障前后电源出口的电流与电压变化量，采用对称分量法求得其三相阻抗矩阵Zabc，进而将DG 等效为理想电压源与阻抗矩阵的串联模型。

1.3 输电线路模型

为了模型的准确性，计及线路的对地导纳矩阵，有源配电网中输电线路采用集中参数模型，由两个对地导纳矩阵和一个串联阻抗矩阵串联而成，其π 型结构如图2 所示。

图2 线路π 型结构

但是对于大部分配电网，三相线路通常采用非换相运行方式，即三相线路存在参数不对称关系（）。本文改进的潮流算法通过利用三相参数进行潮流运算，无需对线路进行解耦处理。

线路的二端口网络如图3 所示，由两个对地导纳矩阵和一个阻抗矩阵级联而成。求取线路的二端口网络矩阵Tl，可得：

图3 配电网线路的二端口网络

则矩阵Tl的可逆矩阵为：

线路末端三相电压和电流与首端电压电流的关系为：

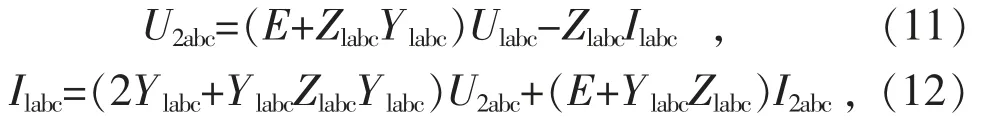
式中：U1abc和I1abc是线路首端的三相电压、电流相量；U2abc和I2abc是线路末端的三相电压、电流相量。

由式（12）变形为：

根据式（12）可知，线路末端电压U2abc和电流I2abc，可求得线路首端电流I1abc；根据式（13）可知，线路首端电压U1abc和末端电流I2abc可求得线路末端电压U2abc。前推回代潮流算法的核心思想：通过不断对支路电流和节点电压进行修正，本节为后续的改进潮流算法做好准备。

2 故障定位算法研究

有源配电网是指DG 通过区域配电网并网运行于电力系统。随着DG 的大量接入，对配电网的安全稳定运行提出了更高的要求和全新的挑战。当有源配电网中发生短路故障时，通过故障定位算法快速定位故障距离，找出故障发生的最小区域，就能够尽快排除故障、恢复供电。因此，有源配电网的故障识别和定位技术是科研人员最为关心的问题。

本文提出的故障定位算法通过计算电源出口电流偏差的最小2-范数来进行故障定位。

2.1 故障定位算法原理

假定有源配电网中含有一个系统电源和n 个DG，在支路i-j 的q 点发生对地短路故障，通过故障电流源If来模拟短路故障。图4 是正常运行情况下的有源配电网简化模型，Ipre是故障前电源出口的三相电流，虚线框中通过相反的电流源If和IF来模拟正常运行情况下的故障点开路状态；故障情况下的有源配电网简化模型如图5 所示，Ipost是故障后电源出口的三相电流，采用等效电流源If来模拟三相故障电流；图6 中通过将所有电源置零，在故障点注入电流IF，其将在电源出口产生三相电流变化测量值Imeasure，其中电流IF与故障电流If大小相等，方向相反，即：

式中：故障电流If和注入电流IF分别是三相电流列向量。

图4 正常运行的配电网简化模型

图5 故障情况下的配电网简化模型

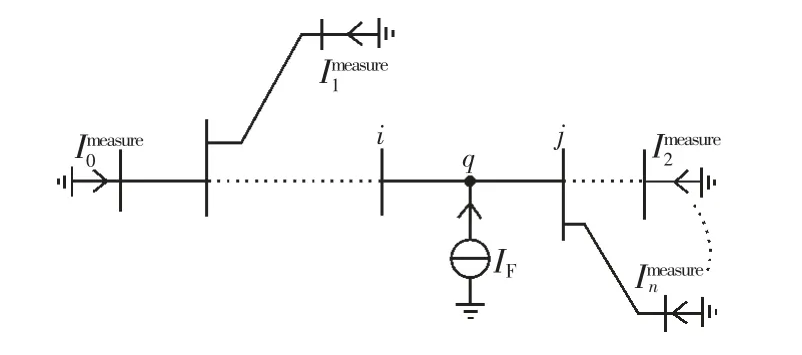
图6 注入电流作用下的配电网简化模型

2.2 注入电流与电流计算值的关系

根据叠加原理，对于任何线性系统，一个含多个独立源的线性电路中的任何支路的响应（电压或电流），等于每个独立源单独作用下响应量的代数和。那么正常运行状态下的有源配电网等于故障情况下的有源配电网和注入电流源IF单独作用情况下的配电网叠加而成，因此，其电源出口故障前的电流Ipre等于故障后的电流Ipost和电流测量值Imeasure的叠加。

图7 注入电流源作用下的配电网简化模型

通过对图6 和图7 进行对比分析可知，当注入电流Iinject和电流源IF的大小和位置相同时，电源出口电流变化测量值Imeasure和计算值Icalculate大小相等，此时电流偏差Ierror（其计算流程将在下文分析）将会存在最小值；当注入电流Iinject和电流源IF的大小和位置不同时，电源出口三相电流变化测量值Imeasure和计算值Icalculate将会存在电流偏差Ierror；由于测量值Imeasure是已知量，因此，其电流偏差Ierror只与注入电流Iinject的大小和位置有关。

2.3 注入位置与电流偏差的单变量函数关系

注入电流Iinject产生的电流偏差Ierror只与其位置和大小有关。本文将通过控制变量法，利用系统电源出口电流变化测量值来修正注入电流Iinject的大小，即当注入位置p 一定时，求解Iinject的大小使得系统电源出口电流变化计算值和测量值相等，进而建立起注入位置p 与电流偏差Ierror的单变量函数关系。

首先，需要将注入电流Iinject分解成基本向量基叠加的电流形式为：

其中：

式中：Iinject为注入的三相电流源；和Iinjectc分别为注入电流Iinject的基本向量基，简称基电流；和k3分别为待求的未知比例系数。

图8 等比例关系

图9 基相量的叠加关系

根据式（15）可知，图7 中三相基电流叠加后的三相电流是注入电流Iinject，叠加后的电流响应值是图7 中各个电源出口电流变化计算值Icalculate。本文可以根据系统电源出口电流变化测量值来计算比例系数k1，k2和k3，令系统电源出口电流变化测量值等于电流变化计算值即：

最后，利用比例系数k1，k2和k3来计算DG出口电流变化计算值通过比例系数k1，k2和k3对DG 出口电流响应值和进行叠加，那么图9 中的DG 出口电流变化计算值与电流响应值的关系是：

2.4 电流偏差Ierror 的计算原理

其中：

第i 个DG 电源出口电流偏差为：

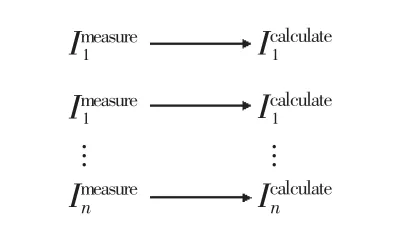
图10 DG 出口电流测量值与计算值

2.5 故障区域的选取

故障区域识别是通过电流偏差Ierror对有源配电网的节点进行优劣评定。假如注入点p 是配电网的节点位置，其电流偏差Ierror越小，表示其离故障区域越近，本文选取电流偏差最小的2 个节点即可确定故障区域。

特殊情况下，当故障点位置接近配电网节点时，尽管可以确定最小电流偏差Ierror的节点，但是确定邻接节点中最小电流偏差Ierror的节点却面临困难。图11 中当故障点q 接近节点n 时，尽管可以确定电流偏差的最小节点是节点n，但是邻接节点n+1 的电流偏差和节点n-1 的电流偏差已经非常接近，其邻接节点n+1 和节点n-1 的电流偏差Ierror的大小已经很难区分。

图11 Ierror 与节点n 的相对关系

因此，当计及随机误差和测量误差的影响，盲目机械地选择邻接节点中最小电流偏差Ierror的节点，极有可能找到错误的节点而识别出错误的故障区域。为了准确识别故障区域，通过设定阈值Δε 来提高故障区域识别的准确度。其阈值Δε为：

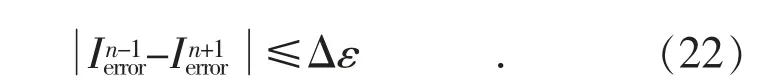
以图11 为例说明，本文选取阈值Δε 是0.05；如式（22）所示，当相邻节点n+1 和节点n-1 的电流偏差Ierror的差值小于Δε 时，可认定故障发生在节点n；当相邻节点的电流偏差Ierror的差值大于Δε 时，仍然选取邻接节点中最小电流偏差Ierror的节点n+1，即故障发生在支路n—n+1 上。

3 改进的前推回代潮流算法

采用前推回代潮流算法来计算电源出口的响应电流。 假定所有负载在故障时期都是恒定阻抗，所有电源电压置零，所有DG 在故障期间被恒定阻抗矩阵代替。通过前推回代法潮流计算来计算电源出口响应电流，此潮流算法可分为前推计算和回代计算2 个过程。

3.1 迭代量的修正

需要对每次迭代的生成量进行修正，通过添加收敛因子ω 来修正生成量，如式（25）所示。

3.2 注入节点的修正

当进行故障区域识别时，需要对配电网节点注入电流源Iinject，此时注入点将会改变节点上下游支路电流关系。当节点连接2 条支路，其中节点n 的父节点是节点n-1，其子节点是n+1；流经上游支路的电流等于下游支路电流、节点n 的负载电流和注入电流之差，即：

当节点连接3 条支路，其中节点n 的父节点是节点n-1，其子节点是n+1 和n+2；流经上游支路的电流由下游支路电流、节点n 的负载电流和注入电流之差，即：

因此，当电流注入点在配电网节点时，将改变上下游支路的电流关系，即上游支路电流等于注入电流与下游支路电流及节点负载电流之差。

3.3 故障定位算法流程

通过有源配电网的故障定位算法原理分析可知，配电网的任意支路发生故障，本算法都可以根据电源出口故障信息，快速准确定地位出故障位置。

故障定位算法的流程图如图12 所示。

4 仿真验证及分析

本文将MATLAB 软件和PSCAD/EMTDC 暂态仿真软件综合利用起来，MATLAB 具有强大的矩阵处理和逻辑运行能力，而PSCAD/EMTDC 软件具有良好的暂态仿真能力。因此，采用PSCAD/EMTDC 软件产生采集的数据信息，利用MATLAB处理和执行此算法。

图12 故障定位算法流程

为了验证所采用的故障定位算法的可行性与有效性，采用改进的IEEE 33 节点配电网系统，如图13 所示。通过在支路末端布置DG 来搭建有源配电网系统，本算例仿真模型在PSCAD 上搭建，采集的数据在MATLAB 上进行分析与处理，进行有源配电网的故障定位分析。

图13 有源配电网故障定位算法仿真模型

将针对特定的故障点具体验证故障定位算法的可行性和有效性，如图13 所示，假定支路8-9的中间位置发生三相对地短路，故障电阻是10 Ω，取收敛因子ω=0.85[14]。

通过对配电网节点注入故障电流，进行电流偏差运算，其电流偏差Ierror与节点n 的关系如图14 所示。其中节点9 的电流偏差最小，其邻接节点中节点8 的电流偏差最小，因此可以断定故障发生在支路8-9 上。

图14 节点n 与电流偏差Ierror 的关系

在配电网故障定位算法中，最常见的智能算法包括GA（遗传算法）、PSO（粒子群算法）与BA（蝙蝠算法）。在上述故障中将基于虚拟电流的注入法分别与智能算法进行横向时间对比分析，其结果如表1 所示。

表1 不同定位算法的时间分析

由分析可知，在收敛条件相同的条件下，注入法运算速度更快。注入法的运算时间只跟潮流算法的运算次数有关，具有线性关系，无需考虑算法的收敛性；而智能算法的运算时间与目标函数有关，不同粒子的目标函数差异越大，运算越快，相反后期的目标函数越接近，运算越慢，具有递减的特性。

验证DG 数目对故障定位的影响，分别在模型不同位置接入不同数目的DG，每次均在32 条支路上设置故障点，结果如表2 所示，均能正确定位故障，而且接入DG 数目越多，对故障定位越有利，其提供的短路电流越大。

表2 DG 接入数目对算法的影响

为分析负荷电流和故障类型对定位的影响，分别测试了IEEE 34 节点系统中接入4 个DG。在32 个支路上做128 次故障（三相短路、单相接地、两相短路、两相接地各32 次），如表3 所示。其中F1，F2，F11 和F3 分别表示单相接地、两相接地短路、两相短路和三相短路。R 表示故障电阻的大小，统计故障区段定位情况如表3 所示。

表3 负荷对故障定位的影响

经过大量实验仿真可知，本文所采用的故障定位算法不受过渡电阻、故障类型以及DG 的影响，具有100%的准确率。

5 结语

本文提出了一种适用于有源配电网的故障定位算法，此算法通过电源馈线接入点的RTU 采用故障信息便可以准确定位故障。通过计算配电网的每个节点进行电流偏差Ierror，搜索最小电流偏差的节点，便可确定发生故障的支路，缩小故障范围。最后通过在PSCAD/EMTDC 上搭建仿真模型，采集的故障信息在MATLAB 上进行算例仿真分析，验证了此算法的有效性和正确性，对于网络中的不同故障点以及不同故障类型，算法都能够精确实现故障区域识别和故障定位，并且此算法的定位精度高，适用范围广泛。