钢管混凝土拱桥扣索一次张拉索力优化改进算法

周 倩，周建庭，陈静雯，冯雨实

(1.重庆交通大学土木工程学院，重庆 400074;2.重庆能源职业学院土木工程系，重庆 402260)

0 引言

大跨钢管混凝土拱桥常采用缆索吊装法架设［1］，这种方法通过缆索吊装系统和斜拉扣挂系统实现钢管拱肋的分段安装.在拱肋悬臂拼装过程中，随着后续扣索的张拉，结构超静定次数逐渐增加，体系不断变化，施工控制难度较大.扣索张拉是调整拱肋架设过程中结构线形的唯一渠道，其索力值直接影响结构松索成拱的线形，如何确定合理的扣索力和预抬量是此类拱桥施工的关键问题之一.当前，扣索力计算中的传统力学方法主要包括:力矩平衡法、零位移法［2］、零力矩法［3］、弹性－刚性支承法［4］等.为避免施工中反复调索的繁琐工作，张治成等［5］运用ANSYS优化模块和生死单元功能优化得到最佳索力.徐岳等［6－7］提出基于影响矩阵和线性规划搜索最佳扣索力的正装迭代方法，并考虑了切向拼装位移影响.刘少平等［8］基于扣索一次张拉法和零阶优化法［9］计算出大宁河大桥施工扣索力和预抬量，指出为减少迭代次数，提高计算精度，可在已有算法基础上作进一步改进.

已有文献算法多以温度荷载作为设计变量，采用自重法估算初始索力，借助程序自动搜索迭代值.研究发现:设计变量迭代初值的确定对迭代次数影响较大，且由于扣索自身变形的影响，于扣索上施加荷载和在拱肋相同位置直接作用等大的力所引起的拱圈变形存在一定差异，为最优解的自动搜索增加了难度.若不能准确给定迭代初值并对程序自动搜索迭代值进行宏观调控，则存在迭代次数较多且最优解获取困难等问题.为此，本文利用ANSYS自带的结构分析功能，基于零阶优化法，提出基于扣索内力法确定迭代初值，并在各子迭代步中对程序自动搜索的迭代变量进行调整的改进算法，以提高迭代效率和计算结果的准确性.

1 基本理论

1.1 优化分析理论

1)数学模型.优化问题的数学模型［10］为:

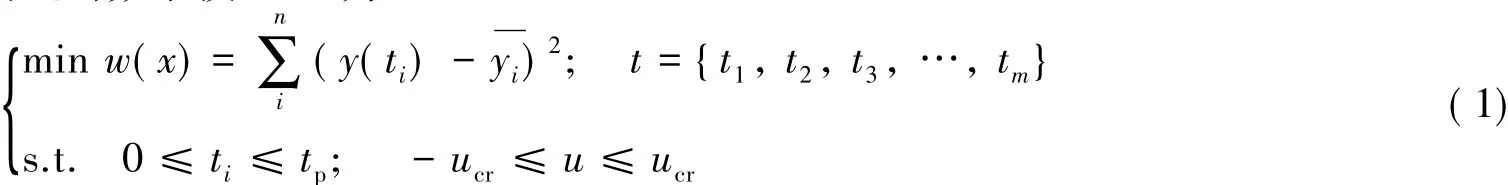
式中:w为目标函数;y(ti)为分阶段施工松索成拱后拱肋扣点位置变形;yi为设计成桥状态自重作用下拱肋扣点位置变形;t为设计变量，本文指扣索力;tp为扣索张拉允许值;m为扣索组数;u为状态变量，本文指扣点位置竖向变形和扣塔水平偏位，分别控制在20和30 mm以内.为提高收敛速度，算法中将变形数值扩大1 000倍，同时目标函数w(x)的收敛公差取为1.

2)零阶优化法.零阶优化法又称子问题方法，其主要思路是基于大量抽样迭代计算，拟合设计变量、状态变量和目标函数的响应函数，寻找最优解.本文使用平方拟合法将目标函数拟合为:

ANSYS中通过罚函数将设计变量及状态变量的约束条件转换为形如下式的无约束方程，实现有约束优化问题向无约束最小值求解问题的转化.

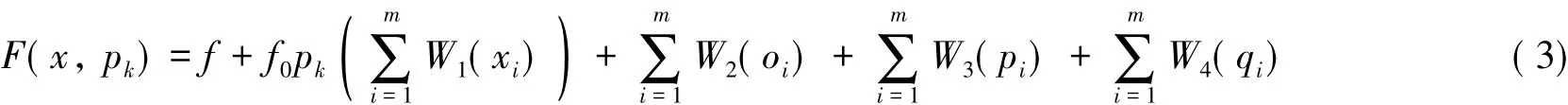
式中:xi为设计变量;oi、pi、qi为状态变量;W1、W2、W3、W4为相应罚函数;f0为目标函数参考值;pk为响应面参数.

1.2 切线初始位移法

拱桥主拱圈预拱度一般采用零初始位移法［11］和切线初始位移法［12］计算.零初始位移法是将待安装单元除共用节点外的其余节点初始位移计为零，以该点记录节点累积位移.切线初始位移法则以安装节段计算节点累积位移起算点为零位置线，沿着前一节段悬臂端切线方向计算待装节段节点位移.钢管混凝土拱桥采用悬臂拼装法施工时，为实现各块段之间无缝拼接，需计入悬臂端各施工阶段产生的切向角位移.

2 扣索一次张拉索力优化算法

2.1 合理安装线形

钢管混凝土拱桥合理成拱状态一旦确定，拱肋各节段的受力状态随之确定.此时若将拱圈拆分成若干个离散单元，卸除杆端力和节间荷载后，单元内力为零，对应各单元的形状就是其无应力构形［13］，即制造线形，在数值上通常等于设计线形加预拱度.对钢管混凝土拱桥，钢拱肋一般采用梁单元模拟，可通过计算梁单元无应力构形确定拱肋节段的无应力构形.只要保证拱肋在初始无应力曲率和初始无应力长度状态下安装合龙，则拱圈成拱后的受力状态不受施工过程影响.

拱肋安装线形为分段安装过程中新增节段前端位置连成的曲线，事实上由于各单元并非同时存在，安装线形是虚拟的，实际安装过程就是逐步恢复构件无应力线形的过程，随着后续节段的安装，各节段间的台阶将逐步消失，最终形成平顺线形.本文通过计算拱肋成桥后在自重和其他荷载作用下的变形反求拱肋安装时的无应力长度，并按照切线初始位移法分段安装，实现拱肋无应力状态合龙(图1).

在图1中，曲线2为设计线形，设其总变形量为s2，成桥后，拱肋在荷载作用下自动逼近线形2.曲线1为计入预拱度后的曲线，即拱肋无应力制造线形，其变形量为s1，拱肋安装时应该按照曲线1进行.

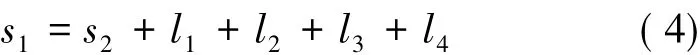
式中:l1为空钢管自重产生的变形;l2为灌注管内混凝土产生的变形;l3为二期恒载产生的变形;l4为混凝土收缩徐变加1/2活载产生的变形.

2.2 零阶优化改进算法

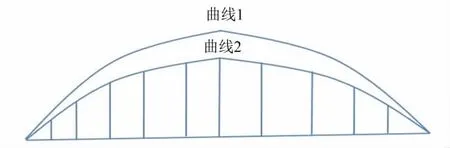
图1 主拱线形示意图Fig.1 Main arch line

原算法流程如图2所示.为更好地对各迭代子步中程序自动搜索的迭代值进行调整，改进算法提出以索力为设计变量，采用内力法确定迭代初值，即先激活零索力扣索单元，以扣索内力作为迭代初值.

为减小于扣索上施加温度荷载和在拱肋上直接施加力引起的主拱变形差异，在各迭代步中提出改进算法，对程序自动搜索的迭代索力进行宏观调整.具体做法为:先将程序自动搜索的迭代索力T1直接施加在拱肋上，拱肋关键截面产生的位移为U0，然后删除拱肋上的力并张拉扣索力T1，拱肋关键截面产生的位移为U1，若 U0－U1＞ε(ε为给定允许范围)，令T2=T1±50，张拉扣索力T2，拱肋关键截面产生的位移为U2.若若U1＜U0＜U2，令T=T2－［(U0－U2)(U1－U2)×(T2－T1)］，以扣索力T进行迭代计算.其算法流程见图3.

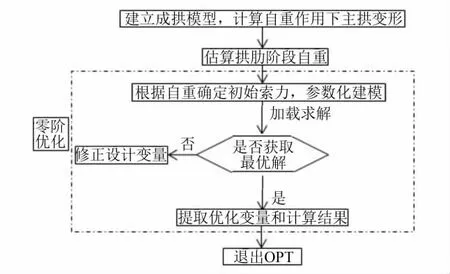
图2 原算法优化流程图Fig.2 Optimization process of original algorithm

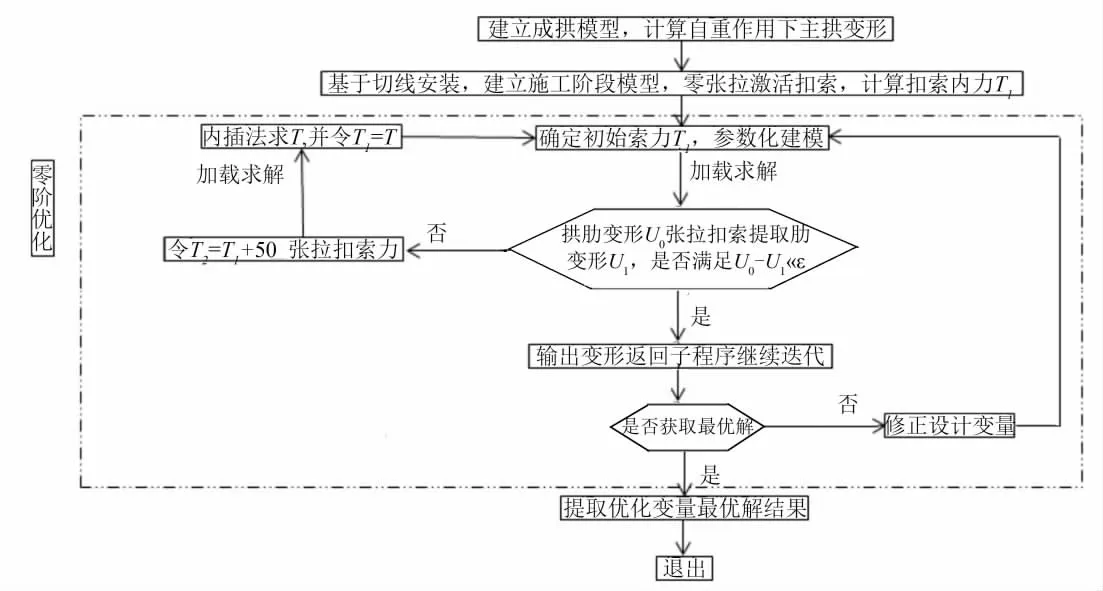
图3 改进算法优化流程图Fig.3 Optimization process of improved algorithm

3 工程应用

3.1 工程概况

某特大桥全桥长839 m，上部结构采用3×30 m先简支后连续T梁+300 m上承式钢管混凝土变截面桁架拱桥+4×30 m先简支后连续T梁的布置形式.主桥桥宽33.5 m，引桥桥宽33.5～40.01 m.主桥采用上承式钢管混凝土变截面桁架拱桥，拱轴线采用悬链线，跨径300 m，矢高54.545 m，矢跨比f=1/5.5，拱轴系数m=1.543.主拱圈采用等宽度变高度空间桁架结构，断面高度从拱顶5 m变化到拱脚9 m.横桥向两片拱肋的中心距离17 m，拱肋间设置横联和米撑.各根弦杆纵向均采用等截面形式，钢管外径均1 200 mm，不同弦杆壁厚不同，壁厚26～35 mm.上下横联采用600 mm×16 mm型号的钢管.拱脚与铰连接处两斜腹杆采用内法兰盘栓接、管外焊接的形式进行连接.管内灌注C55自密实微膨胀混凝土.

半跨拱肋设置12组扣索.上(下)游2#～10#张拉2根扣索，11#～13#张拉3根扣索.1号节段采用型钢支撑，两岸2#～13#扣索锚在交界墩上.张拉端采用自锚式夹片锚，锚固端采用群锚夹片工作锚，并辅以P型挤压锚作保险.扣索由低松弛高强度钢绞线束组成，锚固端采用群锚夹片工作锚和P型挤压锚.

3.2 建立切线初始位移法有限元模型

采用大型软件ANSYS建立吊装节段的有限元模型，主要包括钢拱肋、扣索和扣塔，见图4.主拱圈及钢帽梁采用Q345D钢材，斜拉索采用高强度低松弛七股型钢绞线，抗拉强度为1.86 GPa.钢管拱肋和扣塔采用BEAM44单元模拟，扣索采用LINK10单元模拟.拱肋和扣塔弹性模量取206 GPa，扣索弹性模量取195 GPa.

交界墩底部、背索锚固端采用完全固结方式，拱脚在前八节段吊装时为临时铰接，此后固结.拱圈第一节段吊装时采用型钢临时支撑，模型中采用竖向支座模拟.

图4 有限元模型Fig.4 Finite element model

3.3 索力与预抬量计算

采用改进算法(图3)，经过17次迭代得到5组可行解，采用原算法需经过26次迭代才能找到可行解.改进算法索力计算值同实际张拉索力值以及原算法理论值的对比结果见图5～6.

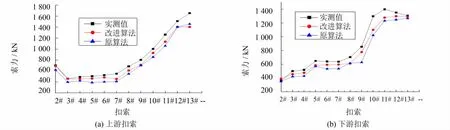
图5 贵阳岸扣索力结果Fig.5 Cable force of Guiyang bank

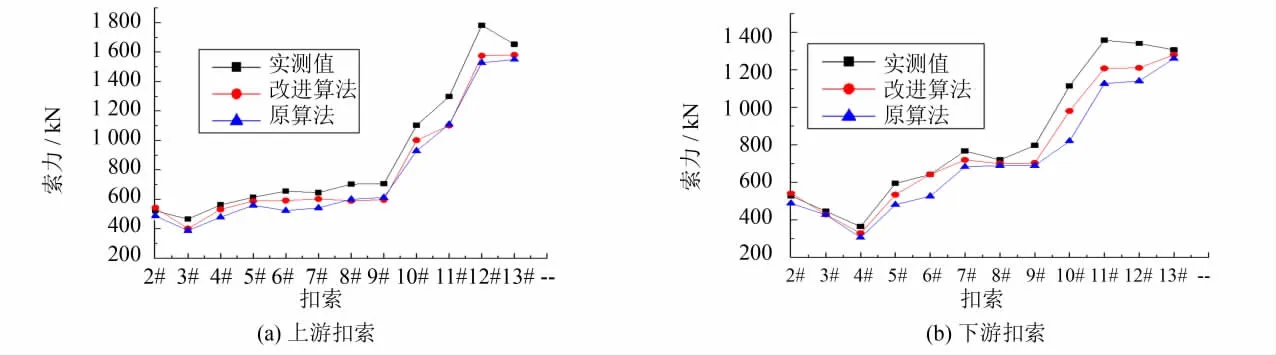
图6 遵义岸扣索力结果Fig.6 Cable force of Zhunyi bank

由图5～6可看出:相比原算法，改进算法得出的索力与实际值更接近，计算精度更高.但由于有限元模型中没考虑扣索管道摩阻力影响，理论计算值均比实际值偏小.张拉7#扣索后，扣索索力实测值和理论值偏差较之前张拉的大，究其原因，该桥在安装7#及之后的节段时进入夏季，最高温差达到35℃，远远超过计算设计温度(12.5±10)℃，使得后安装节段下挠较大，在施工中进行了二次调索.

图7～8给出松索成拱后各控制点的竖向变形.分析可知:按照改进算法优化的索力和预抬量进行分段安装，全桥实测线形和理论线形基本吻合，但拱肋左右两端线形吻合更好，中部后安装节段理论计算值与实测值差距较大，最大偏差接近10 mm，也是由于温度影响使得后安装节段下挠较大造成.此外，预抬量的计算结果表明局部节段设置了负预抬量，此法可保证施工过程中扣索力只发生微小的改变量，从而实现扣索一次张拉，同时确保松索成拱后拱肋线形达到期望值.

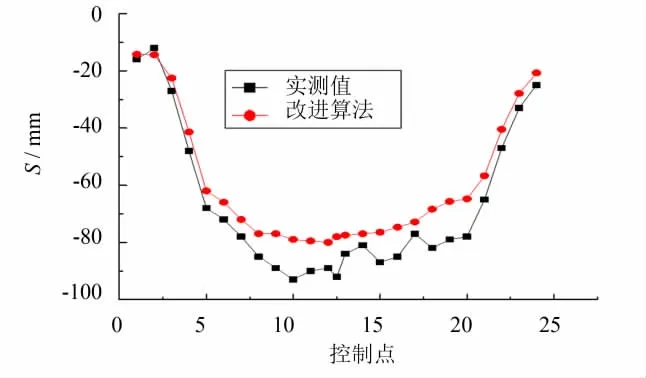
图7 上游拱肋松索成拱竖向变形Fig.7 The into－arch vertical deformation of upstream

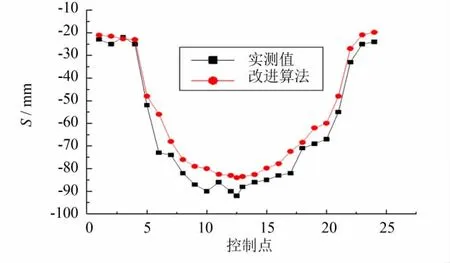
图8 下游拱肋松索成拱变形Fig.8 The into－arch vertical deformation of downstream

4 结语

1)该算法思路清晰、应用简单，提高了迭代效率，在大跨钢管混凝土拱桥扣索力计算中具有较大优势.

2)通过和施工实测值对比，本文提出的改进算法计算吻合度较高，可较好地反映结构吊装过程的受力状态，可实现扣索一次张拉，避免反复调索的繁琐工作，同时能保证拱圈松索成拱后线形满足期望要求.

3)施工温度对拱肋线形和索力影响较大，在实际工程中应提高重视.