30 m预应力超高性能混凝土小箱梁优化设计

马熙伦，陈宝春，黄卿维，苏家战，周家亮

(福州大学土木工程学院，福建福州 350108)

0 引言

预制装配式预应力混凝土梁桥由于具有可批量生产、施工方便、经济效益好等优点，在实际工程中得以广泛应用，但它自重大，容易受吊装与运输条件限制，且在运营过程中，会出现梁体开裂、徐变挠度大等问题.超高性能混凝土(ultra high performance concrete，UHPC)具有高抗压强度、高抗裂性、高耐久性等优点［1］，将其用于装配式桥梁上部结构箱梁中，能利用材料本身优势，减少材料用量，减轻结构自重，提高全寿命的经济效益和社会效益.

针对UHPC箱梁结构，本课题组开展了一系列相关研究工作，建成了一座4～30 m预应力UHPC连续箱梁桥(河北石磁高速公路跨线桥)［2］，并进行了一片30 m预应力UHPC小箱梁的足尺试验.但由于该桥为试验桥，设计相对保守，造价较高，不利于UHPC新材料的推广应用，为此，对其进行优化设计研究.首先，建立30 m预应力UHPC小箱梁的三维实体有限元模型，通过与试验梁结果对比来验证其正确性;然后，对梁内普通钢筋、截面构造与尺寸等进行优化，并进行相应的受力分析;最后，对优化后的箱梁桥进行设计计算及经济效益比较.

1 有限元分析方法

由于目前尚无成熟的UHPC箱梁的极限承载力简化算法和相应的规范，在优化设计时，将应用经试验验证的非线性有限元程序进行计算.

1.1 分析对象

以河北石家庄至磁县高速公路K34+690桩号处的跨线桥为对象.该桥是一座4 m×30 m的连续梁结构，由预制梁先简支后连续方法施工而成.设计荷载为公路－Ⅱ级.桥面宽度为8 m，行车道宽7 m，横截面由3片预制UHPC小箱梁组成，各箱梁中心距2.8 m，顶宽2.3 m，底宽0.9 m，中心高1.6 m，梁内纵向布置3道横隔板.结构详细情况见文献［2］.

在主梁预制时，多制作了一根试验梁，该梁对原结构截面板厚及预应力筋进行了初步的优化.随后进行了足尺模型跨中集中力加载试验.试验结果表明，结构仍有很大的优化空间.

1.2 有限元模型

应用ABAQUS程序，对30 m足尺模型建立精细化数值模型，如图1所示.其中，UHPC箱梁采用八节点六面体缩减积分单元C3D8R模拟，普通钢筋和预应力筋采用三维2节点桁架单元T3D2来模拟，普通钢筋、预应力筋与UHPC混凝土之间采用“嵌入”方法进行自由度耦合，以模拟钢筋及预应力筋与混凝土的良好粘结.计算模型中加载点与支座处设置了刚性垫块，建立了参考点与加载面耦合起来，以防止加载点与支座处因为应力集中导致的局部破坏.模型梁边界条件模拟简支试验梁为铰接约束.

图1 ABAQUS有限元计算模型Fig.1 ABAQUS finite element calculation model

UHPC实测100 mm立方体强度为145.6 MPa，100 mm×100 mm×400 mm的棱柱体抗折强度为17.8 MPa，80 mm×60 mm×60 mm的轴拉试验抗拉强度为8.02 MPa，弹性模量为 42.3 GPa.有限元中 UHPC 本构模型选取混凝土损伤塑性模型，UHPC受压、受拉本构曲线如图2所示.实测预应力钢绞线的抗拉屈服强度为1 950 MPa，弹性模量为205 GPa，实测普通钢筋的抗拉屈服强度为495 MPa，极限强度为620 MPa，弹性模量为201 GPa.有限元中普通钢筋及预应力筋采用理想弹塑性模型模拟.

1.3 有限元模型验证

图3给出了试验梁荷载－跨中挠度曲线有限元计算结果与实测结果的比较.实际试验小箱梁加载至1 815 kN时停止加载，从图3可见，有限元模型梁的计算极限荷载为1 837 kN，实际加载为计算极限荷载的99%，实际荷载－位移曲线与计算荷载－位移曲线二者吻合良好.其中开裂荷载的试验值(出现肉眼可见裂缝)介于500 kN和650 kN之间，根据直接双线性法［3］，出现初裂时的荷载在615 kN，而开裂荷载计算值为619 kN，两者偏差仅为0.65%，验证了计算模型的可靠性.

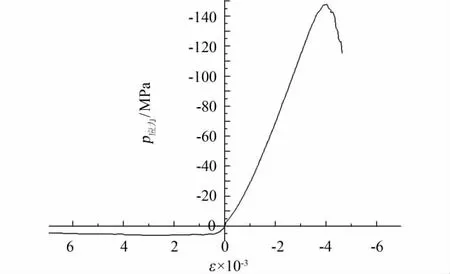
图2 UHPC有限元计算本构曲线Fig.2 Constitutive curve of UHPC finite element calculation

对于裂缝，ABAQUS有限元计算模型无法显示积分点上裂缝的发展，但由于混凝土开裂后即出现拉伸损伤，故可根据拉伸损伤值来表示裂缝分布区域［4］.图4给出试验梁破坏(荷载为1 815 kN)时梁体损伤与试验裂缝分布对比图.从图4中可以看出，计算的开裂范围与试验梁实际开裂位置吻合较好.

对比表明，本研究建立的有限元模型能反映预应力UHPC小箱梁的受力性能，将用于后续的优化设计.

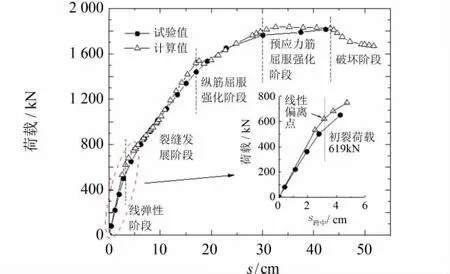
图3 UHPC小箱梁荷载－位移曲线Fig.3 Load－deflection curve of UHPC small box girder

图4 试验梁跨中附近腹板开裂实测与计算对比图Fig.4 Web cracks comparison of test and calculation near the mid－span of the test beam

2 优化设计分析

2.1 材料设计指标

UHPC材料参照文献［5］，采用U130，即100 mm立方体抗压强度标准值不小于130 MPa，相应的棱柱体弹性模量要求不低于40 GPa.UHPC的材料设计指标如表1所示.

表1 UHPC13材料设计指标Tab.1 UHPC13 material design indexes

根据我国公路规范［6］，预应力钢绞线的设计指标为抗拉强度标准值1 860 MPa，抗拉强度设计值1 260 MPa，弹性模量195 GPa.HRB400普通钢筋的设计指标为抗拉强度标准值400 MPa，抗拉强度设计值330 MPa，弹性模量200 GPa.

2.2 钢筋优化

UHPC由于具有极强的抗压强度和一定的抗拉强度，其抗开裂能力、抗弯强度和抗剪强度均较普通混凝土有很大的提高.在UHPC的应用与研究中，减少甚至不用普通钢筋的例子很多.如，法国2001年建成的Bourg－lès－Valence OA4桥［7］的UHPC主梁未配置普通钢筋，德国2007年建成的Grtnerplatz桥桥面板为不配普通钢筋的UHPC构件［8］，捷克2015年建成的Celakovice人行斜拉桥的UHPC梁板式主梁未配置普通钢筋［9］，福州大学2015年建成的校园人行桥为素UHPC拱［10］，马来西亚修建的多座UHPC梁桥［11］主受力方向也均为不配钢筋的UHPC结构;文献［12－13］研究了不配箍筋的UHPC梁的抗剪性能，利用UHPC高强的抗拉作用相当于普通混凝土梁中箍筋的贡献.UHPC少配甚至不配钢筋，不仅能节约材料的费用，而且减轻或免除了钢筋加工、制作这一工厂化、预制化最耗人工的工序，也减缓或避免了钢筋锈蚀这个钢筋混凝土结构最主要的耐久性问题.因此，首先开展UHPC小箱梁的钢筋优化设计研究.

UHPC实桥的小箱梁底板配置9根直径25 mm的HRB400级纵向受拉钢筋，纵筋配筋率为0.67%.以此为基础，减少钢筋用量，形成4个优化方案.方案一将纵筋改为9根直径22 mm的钢筋，纵筋配筋率减为0.52%，箍筋及构造筋不变;方案二将纵筋改为9根18 mm的钢筋，纵筋配筋率减为0.35%，箍筋及构造筋不变;方案三不配置纵筋，纵筋配筋率减为0%，箍筋及构造筋不变;方案四不配置纵筋，纵筋配筋率为0%，且不配所有箍筋及构造筋，普通钢筋配筋率为0%.

修改相应的有限元模型，计算的结构受力全过程荷载－跨中挠度曲线如图5所示.从图5可知，减少甚至取消纵向受拉钢筋以及箍筋和构造钢筋，对箱梁的受力规律没有根本的改变.

将原桥中公路II级正常使用极限状态设计荷载组合、承载能力极限状态设计荷载组合及2倍汽车活载承载的能力极限状态设计荷载组合得到的作用效应，根据跨中弯矩等效的原则换算为试验箱梁的施加荷载，分别相应为332、692和1 177 kN，用虚线标于图5中.这些值均小于4个方案中梁的极限承载力，因此，即使方案四中完全不配普通钢筋(包括纵向受拉钢筋、箍筋和构造筋)，小箱梁仍能满足公路II级荷载的设计承载力计算要求.

表2对比了不同钢筋优化方案的设计承载力.由表2可知，随着纵筋配筋率的降低，箱梁的承载力逐渐降低，纵筋对预应力UHPC箱梁的承载能力有明显的提高作用.纵筋配筋率降低了0.67%，箱梁极限承载力降低了19%;减少所有普通纵筋、箍筋和构造筋量，箱梁极限承载力降低了20%，箍筋及构造筋对UHPC箱梁的抗弯承载力贡献有限.

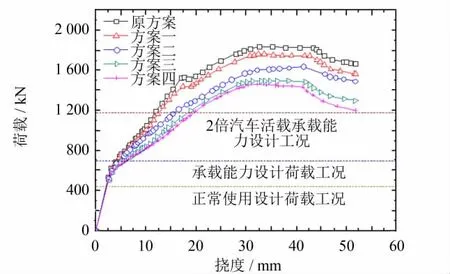
图5 钢筋优化荷载－位移曲线对比图Fig.5 Load－displacement curve comparison of reinforcement optimization

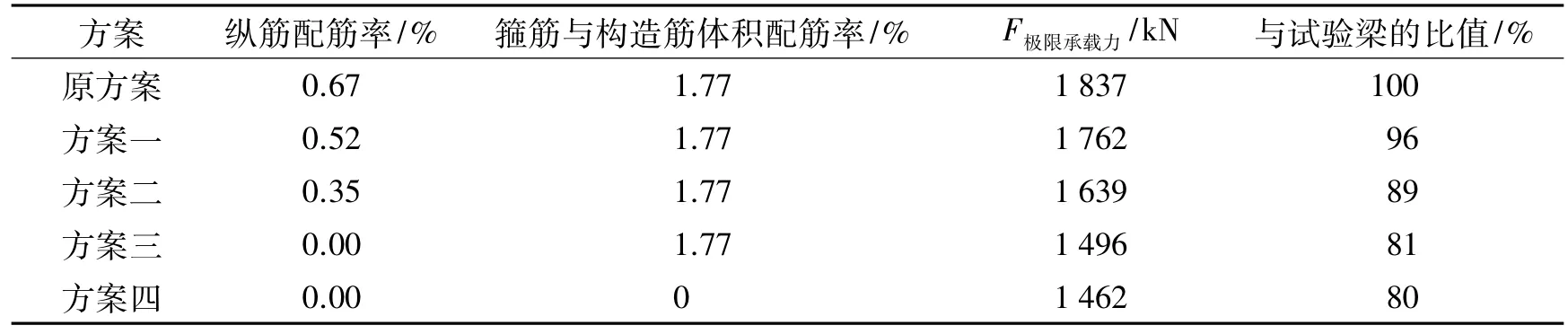
表2 不同钢筋优化方案设计承载力对比表Tab.2 Design bearing capacity comparison of different reinforcement optimization

2.3 箱梁壁厚优化

从材料强度自身要求出发，UHPC箱梁的壁厚可以很薄，但对于预应力UHPC结构，通常受预应力筋管道的要求而变厚.将预应力筋改为体外索，是减薄壁厚一个常用的方法.此外，体外索具有可检查、易更换、索力可检测及可补张拉等优点，在许多已建的UHPC桥梁中得以应用.如法国2005年建成的PS34桥，为跨径47.4 m的UHPC箱形梁桥，箱梁宽4.4 m，高1.63 m，顶板厚14 cm，腹板和底板厚12 cm，采用体外预应力束［14］;奥地利2010年建成的Wild桥，其拱肋为不配钢筋的预应力UHPC构件，采用体外索［15］，拱肋壁厚仅为5 cm.

在上述钢筋优化的基础上，对箱梁的壁厚(主要是底板厚度)进行优化.考虑到板厚较薄，采用体外预应力筋，体外预应力筋布置见图6.与原桥相同，顶板厚度仍为8 cm，支点截面腹板厚度为12 cm，一般截面腹板厚度为8 cm.将支点截面底板厚度由原桥的24 cm减薄为12 cm，一般截面底板厚度由15 cm减薄为8 cm，为方案五.

原桥4～30 m连续箱梁桥底板最大压应力出现在支点截面底板处，将支点截面底板作为箱梁板件厚度优化的应力控制点，采用MIDAS Civil建立连续箱梁有限元模型，比较方案四和方案五，分析得到持久状况荷载组合的支点底板主压应力及长期效应组合的跨中挠度结果，列于表3.

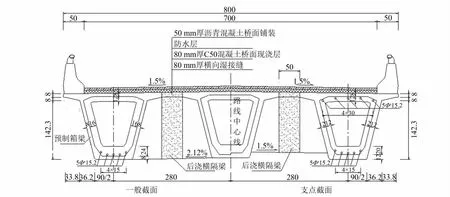
图6 优化后的横截面尺寸与预应力筋布置图(单位:cm)Fig.6 Optimized layout of transverse section size and prestressed reinforcement(unit:cm)

表3 底板优化数据分析表Tab.3 Data analysis table of bottom slab optimization

由表3可知，随着底板厚度的减小，正常使用极限状态下，支点底板压应力由－24.70 MPa增大为－25.87 MPa，持久状况和短暂状况下，底板主压应力由－26.76 MPa增大为－27.20 MPa，底板压应力随板厚的减小而增大;挠度由16.1 mm增大为19.2 mm，挠度亦随之增大.

根据我国公路规范［6］相关规定，持久状况下截面的主压应力应低于UHPC抗压强度标准值fck的0.5倍(0.5 fck=0.5×91=45.5 MPa)，主梁挠度应小于跨径l的1/600(l/600=50 mm)，考虑20%的强度储备，UHPC压应力的限值约为36.4 MPa.表3中，底板压应力及挠度均满足设计验算要求.

2.4 横隔板设置分析

为了研究横隔板的作用，在上述方案四的基础上，通过调节横隔板间的距离，考察公路II级设计车辆荷载作用于箱梁翼缘时(两辆车轮荷载沿30 m箱梁翼缘位置纵排布置)结构的受力情况，计算结果列于表4.

表4 不同横隔板情况下UHPC箱梁的应力及位移Tab.4 UHPC box girder stress and displacement under different diaphragm conditions

从表4可见，横隔板可减小横桥向最大拉应力及横桥向的正应力，多横隔板(每隔5 m设置1道)时的横桥向最大拉应力及横桥向正应力峰值分别为7.15和3.29 MPa，小于少横隔板(每隔15 m设置1道)时的7.19和3.93 MPa，二者均小于UHPC的抗拉强度设计值5.35 MPa.同时，多横隔板时截面翘曲变形最大值为1.203 μm，略小于少横隔板时的变形最大值1.223 μm，横隔板在减小箱梁横桥向应力及翘曲变形有一定的作用.总之，由于所研究的梁跨度、截面均较小，箱梁的翘曲畸变效应不明显.因此，本优化设计中横隔板不采用原桥的设计(每隔7.5 m设置1道)，仅在跨中和支点位置布置12 cm厚的空心横隔板(每隔15 m设置1道).

3 优化后的UHPC小箱梁桥设计计算

根据节2的优化分析，优化后的UHPC小箱梁，除端部预应力锚固区少量钢筋外不配普通钢筋，仅在跨中和支点位置设置12 cm厚的空心横隔板，改变底板厚度，其余按原设计.其中，连续UHPC箱梁顶部、底部体外预应力钢绞线均布置为5根5s15.2.优化后的横截面见图6.

梁格法建立4～30 m预应力UHPC连续箱梁的MIDAS Civil有限元模型.相关材料参数均参照材料设计指标，支座采用一般支承模拟.计算时，设计作用与组合与原桥设计相同.结构荷载效应包括:自重、桥面铺装、防撞护栏、预应力以及车辆活载，构件按A类构件设计，并对UHPC箱梁桥进行相应的承载力、抗裂、挠度及应力验算，验算结果列于表5.表5中，对预应力混凝土A类预制拼装构件，在短期效应组合下，正截面抗裂及斜截面抗裂正截面及斜截面混凝土的主拉应力应低于UHPC抗拉强度标准值ftk的0.7倍(0.7 ftk=0.7×7.8=5.46 MPa)［6］.

表5 优化UHPC小箱梁承载力、抗裂及挠度验算Tab.5 Optimized UHPC small box girder bearing capacity，crack resistance and deflection check calculation

由表5可知，UHPC箱梁各项指标均满足规范的相关规定，并具有一定的安全储备，表明该优化的30 m预应力UHPC箱梁桥结构能够满足承载力及正常使用的要求.

4 经济效益分析

优化后4～30m预应力UHPC桥(ZPU)的主梁工程造价与预应力普通钢筋混凝土桥(PC)、原桥(PU)相比，比例分别为1.04与0.67，与普通钢筋混凝土梁相近.ZPU与PC比，ZPU的UHPC材料、预应力筋和普通钢筋的用量为PC的57%、91%和4%，材料造价比为136%.ZPU与PU比，UHPC材料、预应力筋和普通钢筋的数量为PU的65%、88%和6%，材料造价比为56%.可见，ZPU节省了大量普通钢筋的用量.此外，UHPC具有良好的耐久性［20］，从全寿命桥梁的经济效益看，具有很强的竞争力.

5 结语

1)通过三维实体有限元模型成功模拟了足尺箱梁试验模型，对其受力全过程进行分析，其中开裂荷载的试验值与计算值两者偏差仅为0.65%，计算结果与试验吻合良好，表明本研究建立的有限元模型和所采用的分析方法是可行的.

2)开展优化钢筋的有限元参数分析，结果表明，纵筋配筋率降低了0.67%，箱梁极限承载力降低了19%;减少所有普通纵筋、箍筋和构造筋量，箱梁极限承载力降低了20%，箍筋及构造筋对UHPC箱梁的抗弯承载力贡献有限.无普通钢筋的预应力UHPC箱梁的承载力仍能满足设计验算要求.

3)采用体外预应力，对箱梁的底板厚度进行优化，将支点截面底板厚度由原桥的24 cm减薄为12 cm，一般截面底板厚度由15 cm减薄为8 cm.随着板厚的减薄，底板主压应力由－26.76 MPa增大为－27.20 MPa，挠度由16.1 mm增大为19.2 mm，仍满足验算要求.

4)模拟公路II级车辆偏载作用，分析加密横隔板对UHPC箱梁的横桥向应力及翘曲变形的影响，虽然横隔板间距小些在减小箱梁横桥向应力及翘曲变形有一定的作用，但所研究梁的跨度、截面均较小，箱梁翘曲畸变效应不明显.因此，可不加密.

5)对优化后的4～30 m预应力UHPC箱梁桥进行了设计验算，其受力性能均满足设计验算要求.通过经济效益分析，优化后桥的主梁工程造价与普通钢筋混凝土梁相近.从全寿命周期考虑，经济效益明显.