基于理论模型及其差分方程的湖北省杉木立地指数表研制

李斌成，杜超群 ，袁 慧，吴 楚，陈书杭，曾 勇，许业洲

（1.长江大学，湖北 荆州 434025；2.湖北省林业科学研究院，湖北 武汉 430075；3.咸宁市林业科学院，湖北 咸宁 437000 ；4.恩施市林业科学研究所，湖北 恩施 445000）

杉木是我国特有针叶用材树种，栽培历史悠久，广泛分布于我国亚热带山地、热带北缘和暖温带南缘等气候区的18 个省区。因其速生、材质优良、干形通直圆满,深受人们喜爱[1-3]。立地指数的概念最早产生于18 世纪，并被作为评价立地生产潜力的指标，即利用林分中平均优势高和年龄的关系，以基准年龄时的优势高作为衡量立地生产潜力的指标[4-6]。立地指数目前已作为林分生长和收获模型中的变量因子，直接参与模型的运算，并作为参数影响模型预测结果，从而提高预测林分直径、树高生长量和收获量等的精度[7]，更准确地反映人工林的立地条件和林分生长力[8]，是开展森林生长预测、森林经营效果以及其他经营管理工作的基础。

对于立地指数曲线的研制，主要有导向曲线法、差分方程法以及参数预估法这3 种方法。导向曲线法是直接利用理论方程通过比例调节来编制立地指数表。差分方程法是理论方程变换形式，能保证基准年龄时树高与立地指数一致，这种方法表现更为灵活，已日渐成为主流研究方法。而参数预估法是将理论方程中的参数表达为立地指数函数，但无法保证基准年龄时的树高值与立地指数值一致。

近年来，国内外学者编制了大量树种的立地指数表用于评定立地质量、指导生产实践或预测林分树高生长和蓄积量，都取得了很好的效果[9-12]。张伟[13]等利用290 组树高-年龄数据，使用相对优势高法编制了山东省侧柏立地指数表，其精度较高且能适用于山东省侧柏人工林立地质量评价；韩培新[14]利用93 块标准地数据，使用标准差调整法编制了韶关市尾巨桉、巨尾桉短周期工业原料林立地指数表，能较好反映当地桉树树高和立地条件的关系。段爱国等[15]利用157 株杉木解析木数据，采用差分方程构建了以5 种理论方程为基础的多种多形地位指数方程，指出理论方程与多形立地指数方程在编制立地指数表时各自的优缺点；李品德[16]等利用二类清查数据编制了精度高、适用性强的广南县杉木立地指数表；朱光玉[17]等利用606 组杉木纯林优势木平均高-年龄数据，采用循环迭代法结合最优基础模型，对树高-年龄进行分级，借助含哑变量的非线性回归进行分级结果检验，结果表明分级哑变量等级值越大，优势木生长越好，立地质量越好。

湖北地处我国杉木栽培北缘地带，在鄂东南、鄂西南等地均有多年栽培历史，杉木是湖北低山丘陵地主要造林树种和重要针叶用材树种，人工林面积占全省人工林面积的40%。但湖北杉木人工林的立地质量评价和林分生产力预估等方面的研究较少，目前仍处于空白，未见相关报道。本研究以全省杉木分布区标准地调查和优势解析木资料为基础，采用理论生长方程及其差分方程构建树高生长模型，并利用导向曲线法和差分方程两种方法编制湖北杉木人工林立地指数表，以期为湖北杉木造林、分类经营及林分定向培育提供参考和支持。

1 材料与方法

1.1 试验区概况

湖北省地处长江中游，位于108°21′42″～116°07′50″E、29°01′53″～33°6′47″N。全 省 地 势大致为东、西、北三面环山，中间低平，略呈向南敞开的不完整盆地，山地面积占全省总面积的56%，丘陵占24%，平原湖区占20%。省内最高海拔3 105 m，平原区大部分约为20～100 m，属亚热带季风气候区。年平均气温15～17 ℃，无霜期230～300 d，年平均降水量800～1 600 mm，气候湿润，雨热同季。全省境内除江汉平原和鄂北岗地外，其他低山丘陵地区均有杉木栽植，但主要栽培区域分布在鄂南幕阜山系、鄂西南巫山山系、鄂东大别山山系等。

1.2 数据来源

分别在杉木人工林主要分布区的6 个地区11个县市区，按典型抽样和随机抽样相结合的方式，在造林面积大于15 hm2的人工林中选取不同年龄、不同立地林相完整的林分设置面积为600 m2（20 m×30 m）的标准地，标准地内每木检尺，测量胸径、树高、枝下高、冠幅等生长量指标，并记录地理位置、立地环境及造林年度、造林密度等信息。每块标准地中以生长量最大的5 株优势木的树高平均值为优势高，并选取1 株优势木按2 m 区分段进行树干解析，获取树高生长量与年龄等数据资料，经内业整理选出92 个标准地及其优势解析木的解析资料为本研究基础数据。标准地及优势木信息见表1。

1.3 优势高生长方程的模拟

1.3.1 理论生长方程

选择7 个常用的理论生长方程，运用Sigma Plot 10.0 程序中的Dynamic Fit Wizard-Epuation 模块对树高-年龄配对数据进行拟合，各方程表达式如下：

表1 标准地及优势木基本信息†Table1 Basic information of standard land and dominant wood

式（1）～（7）中：H为优势高，t为年龄，a，b，c为待定参数，其中a为树高生长的最大值。

1.3.2 差分方程

根据理论方程的模拟结果，并参考段爱国[15]的相关研究，选择理查德、逻辑斯蒂、考尔夫、威布尔、舒马赫等5 个理论方程进行差分运算，分别得出对应的差分方程表达式。运用SPSS17.0程序中的非线性回归模块，对双树高-双年龄数据进行差分方程的拟合，得出不同方程及不同自由参数的差分方程。

Richards(自由参数b)：

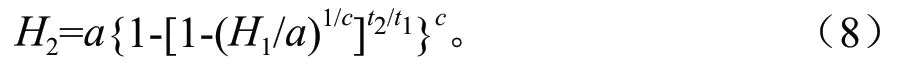
Richards(自由参数c)：

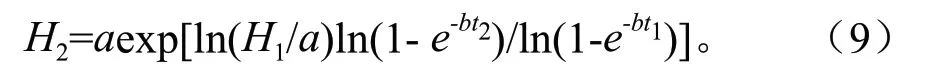
Richards(自由参数a)：

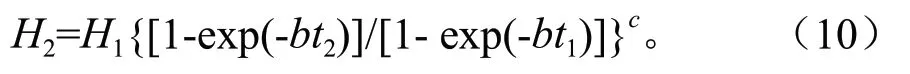
Richards(三参数)：

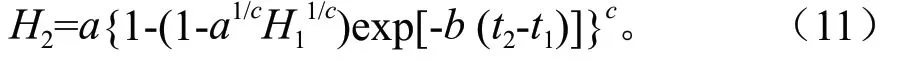
Logistic(自由参数b)：

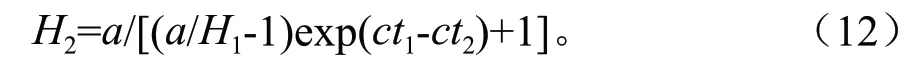
Korf(自由参数b)：

Weibull(自由参数b)：

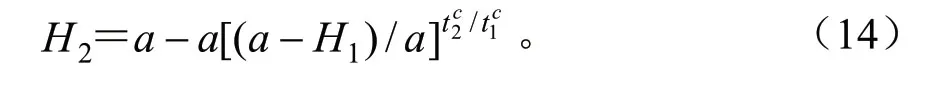
Weibull(三参数)：

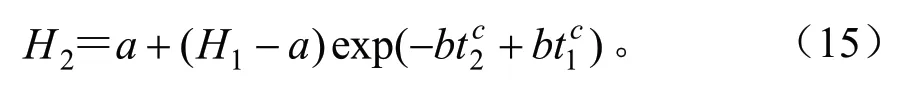
Schumacher(自由参数b)：

1.3.3 模型选择

以模型及其参数的生物学意义为前提，选用平均残差（MR）、绝对残差（AMR）、相对残差（RAR）、残差平方和（RSS）、均方根误差（RMSE）以及决定系数（R2）等6 个常用统计指标来评估模型的拟合质量（统计指标计算公式见文献[15]）。选择R2大，AMR 和RMSE 较小且具有生物学意义的方程作为树高生长方程。

1.4 立地指数表的编制

1.4.1 标准年龄与指数级

标准年龄与指数级的确定方法参照韩培新[14]关于韶关市巨尾桉立地指数表的编制。

1.4.2 单形立地指数表的编制

以最优的优势高生长方程为导向曲线，采用相对优势高法[18]编制单形立地指数表。具体计算公式如下：

式（17）～（18）中：Kj为各指数级的调整系数，Hoj为标准年龄时j指数级的树高值，Hij为各龄阶指数级树高，Hik为各龄阶树高理论值，Hok为基准年龄时的树高理论值。

1.4.3 多形立地指数表的编制

选择较优的差分方程作为基础方程，设H=H2，t=t2，SI=H1，T=t1，其中SI、T分别表示立地指数和指数年龄，将各变量代入差分方程求出各年龄优势高即为立地指数表。

1.4.4 立地指数表检验

选择52 株（占总株数56.5%）年龄大于20 a的优势解析木资料作为立地指数表的检验数据（表2），按基准年龄树高值以2 a 为一个龄阶进行分组，求出各龄阶树高平均值，利用公式（19）将各龄阶平均树高换算成基准年龄时树高，得到检验样本的立地指数，分别按公式（20）计算不同组别的χ2值，进行立地指数表的显著性检验。按公式（21）～（22）计算不同年龄（龄组）和不同立地指数级的估计误差值，进行立地指数表的预测精度检验。

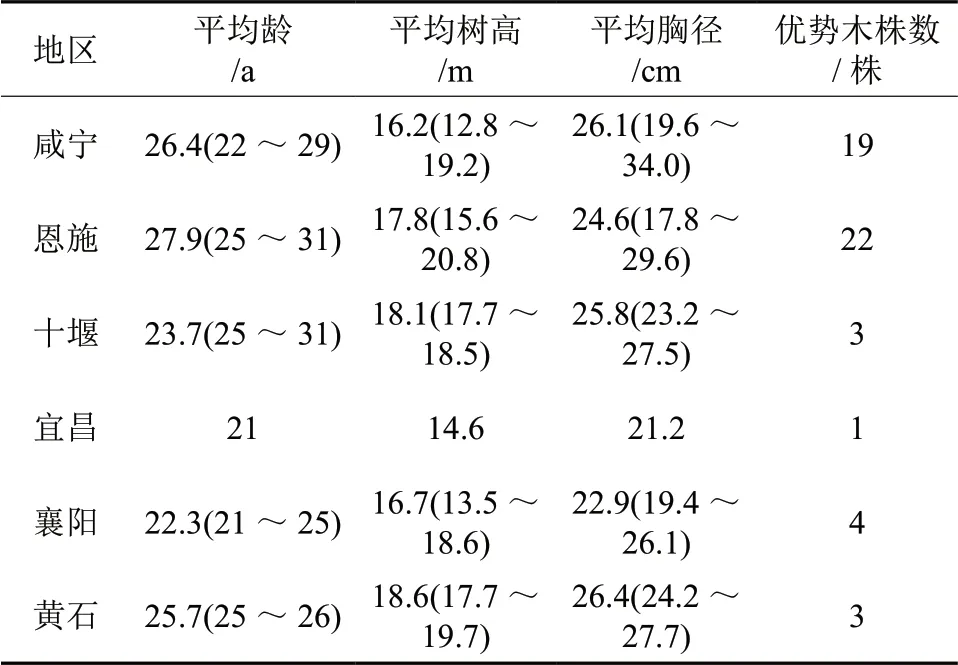
表2 检验样本基本信息Table2 Basic information of test samples

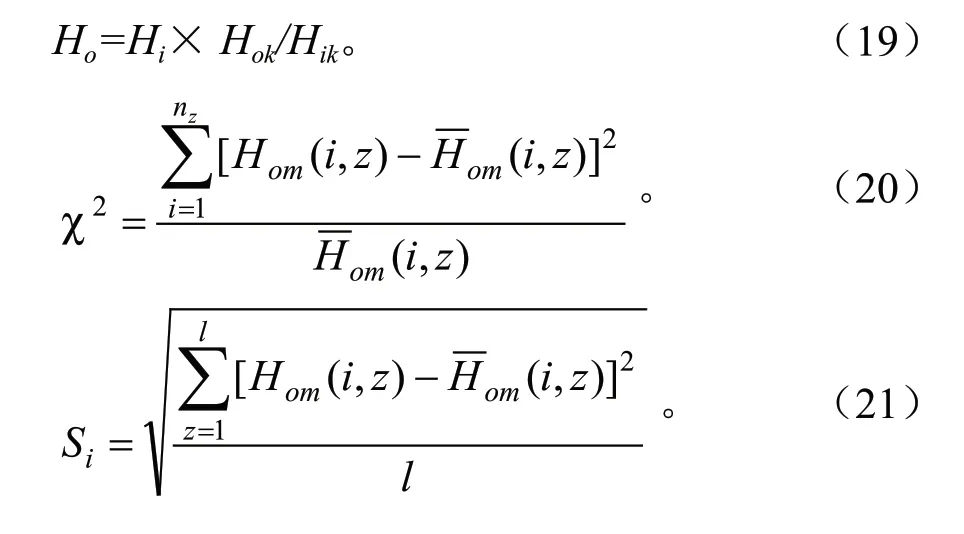
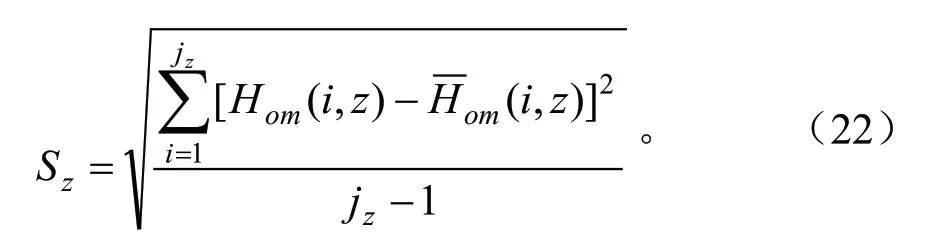
式中：Ho为立地指数，即基准年龄时的树高，Hi为第i龄阶平均实际树高值，Hok为基准年龄时的导向曲线树高，Hik为第i龄阶导向曲线树高，Hom(i,z)为年龄为i，立地指数为z时的实际树高值，(i,z)为年龄为i，立地指数为z时的平均树高值，Si为立地指数估测误差，Sz为龄阶估测误差。

2 结果与分析

2.1 树高生长模型拟合

2.1.1 拟合结果与检验

各理论模型及差分方程的拟合结果及各统计指标值见表3。从表3中可以看出，理论方程的R2为0.857 9～0.873 2，除MR 差异较大外（-0.570 4～0.206 4），其他统计指标均较为相近，整体拟合效果较好，除方程1 和方程4 的参数值异常之外，其他方程参数值均具有较好的生物学意义。经综合评判选择方程2（理查德模型）为最优树高生长模型，其R2最高（0.873 2），AMR、RSS、RMSE 均为最小。

差分方程的R2绝大多数在0.99 以上，AMR和RMSE 分 别 在0.277 3～0.745 9 和0.359 4～0.502 2，除方程13 参数异常外，其他方程参数均具有较好生物学意义。相比较而言，理查德模型的4 个差分方程拟合精度优于其他差分方程，其中方程9（理查德：自由参数c）拟合优度0.9953为最高，而RAR、RSS 及RMSE 最小，拟合效果最优。

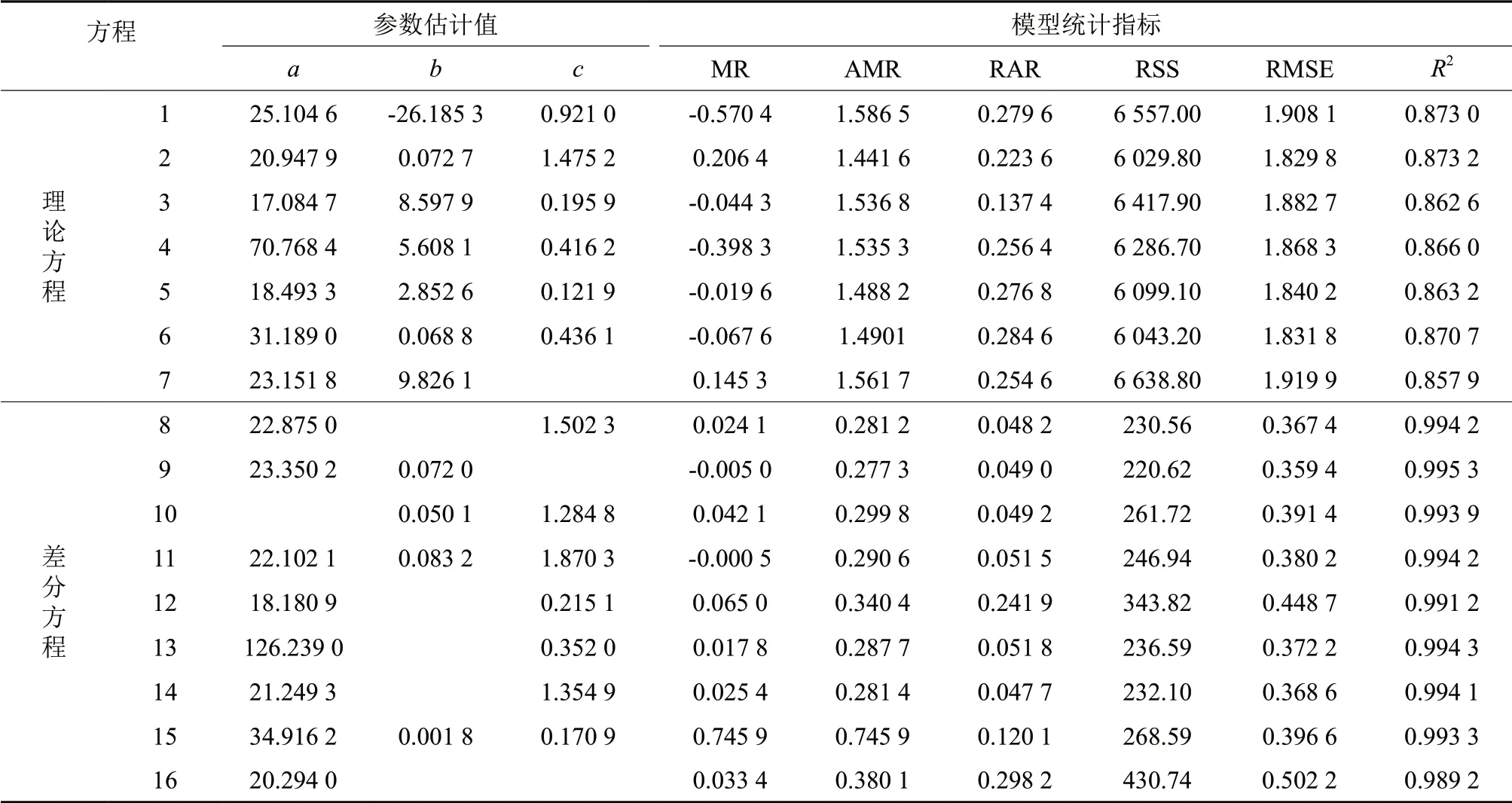
表3 各生长方程拟合结果及统计指标Table3 Fitting results and Statistical Indices of each growth equation

2.1.2 2 种建模方程的比较

从2 种建模方程的拟合结果可以看出（表3），差分方程的拟合效果普遍优于理论方程。以理查德模型及其差分方程进行综合比较，后者R2提高13.8% 以上，而AMR 和RMSE 均减小至前者的0.2 倍左右，而RSS 只为前者4%，差分方程显著提高了方程的拟合精度。分别对拟合效果最好的理论方程（方程2）和差分方程（方程9）进行残差分析（见图1），结果表明：2 种方程的残差中值都接近0，理论方程的残差波动范围在-5～6 m，残差绝对值随着年龄的增大呈先增大后减小的趋势，而差分方程的残差波动范围在-1～2 m，残差绝对值随年龄的增大逐渐减小，差分方程的残差分布范围和变化趋势优于理论方程。

2.2 立地指数表的编制

2.2.1 标准年龄及指数级的确定

利用92 株杉木解析木资料计算各龄阶树高变动系数，由表4可以看出，树高变动系数总体趋势为随年龄增大而逐渐减小，至20 a 后相对稳定。考虑到杉木中径级材轮伐期为20～30 a，且杉木在20 a 时解析木材料分布比较均匀，因此，选择20 a 为编制湖北杉木立地指数表的基准年龄。

图1 2 种方程的残差分析Fig.1 Residual analysis of two equations

表4 各龄阶树高变动系数Table4 Coefficient of variation of tree height by age

20 a 优势木树高变动范围为10.3～19.5 m，树高绝对变动幅度为9.2 m，以2 m 为级距可确定6 个指数级，但兼顾杉木在全省所处立地条件的差异性与复杂性，为保证立地指数表有较大容量，将立地指数向两侧各延伸一个指数级，确定指数级8个，分别为8、10、12、14、16、18、20 和22。

2.2.2 单形立地指数表的编制

选择最优理论方程2为导线曲线，表达式如下：

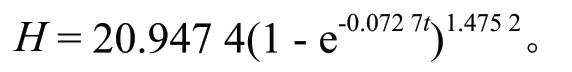
式中：H为优势树高，t为优势木年龄

利用公式（17）～（18）求出各指数级调整系数及各龄阶各指数级树高值，编制出湖北杉木人工林单形立地指数表（表5）。

2.2.3 多形立地指数表的编制

差分方程中拟合效果较好的依次为方程8、方程9、方程14 和方程13，为了评估4 个方程是否满足立地指数表模型的生物学假设，将4 个方程按20 a 为基准年龄，2 m 指数级距绘制立地指数曲线簇（图2）。

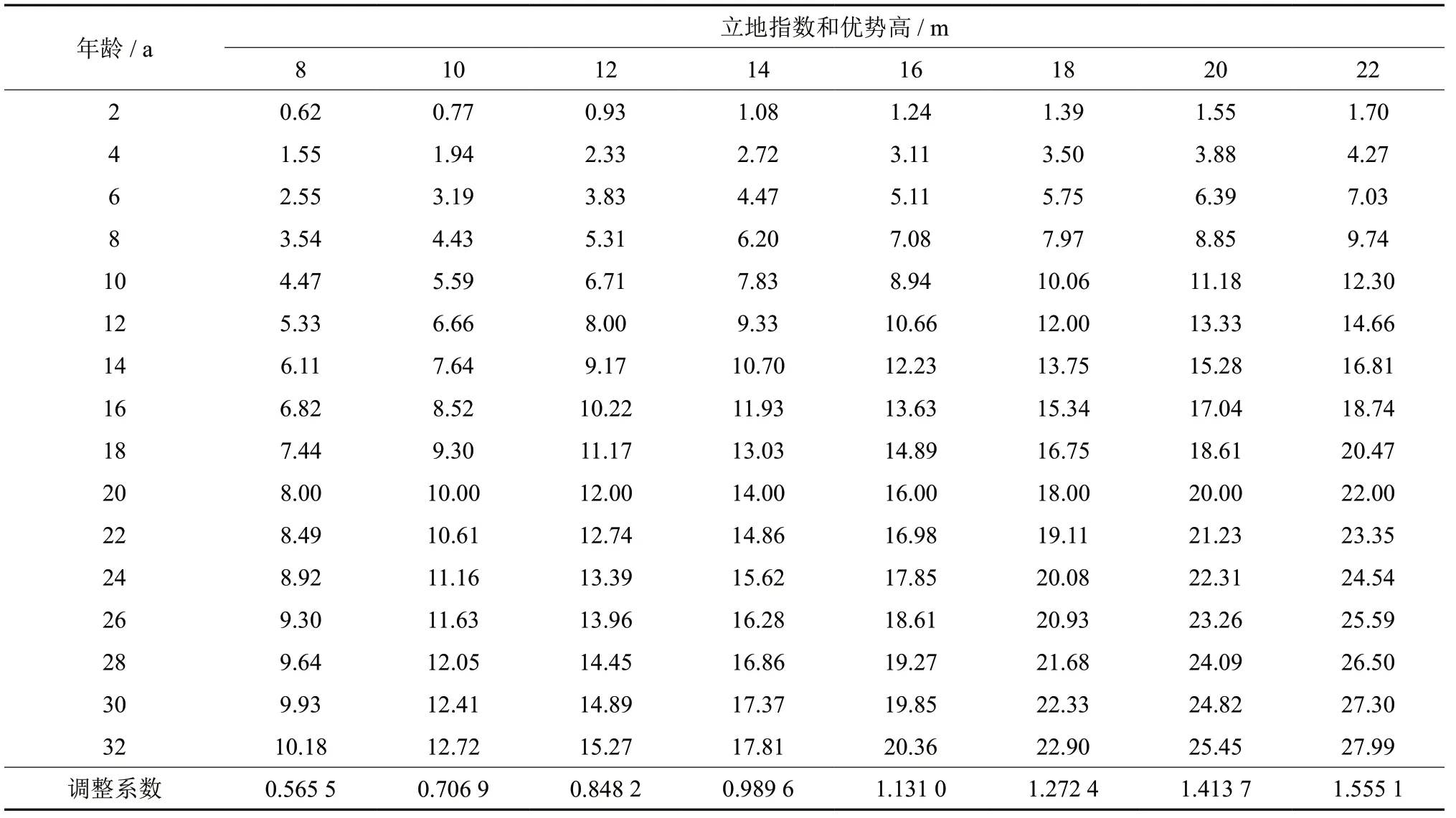
表5 湖北杉木人工林单形立地指数表Table5 Simplex site index table of Chinese fir plantation in Hubei

图2 模型立地指数曲线簇Fig.2 Model site exponential curve cluster

由图2可以看出，方程8 在高指数级的低年龄段树高值偏大，且随着龄阶向两端外延时方程受到限制而无法计算；方程9 在立地指数级22 时出现异常且在低指数级低龄阶树高值偏小，不符合杉木树高生长规律；方程14 在高指数级（22）和高龄阶时受限不能运算，只能形成不够完整的立地指数曲线簇；方程13 具备多样性、S 形生长曲线并具有多条水平渐进线，符合理想的立地指数模型特征，故选择方程13 为编制多形立地指数表的基础方程，表达式为:

标准年龄T=20 a，将立地指数SI和年龄t 代入上述多形立地指数方程，可求出杉木人工林不同年龄的优势高预估值，将其整理便可得到湖北杉木人工林多形立地指数表（表6）。

2.3 立地指数表检验

将检验样本分组，计算各龄阶树高平均值，分别利用公式（19）和差分方程13 计算相应的单形和多形立地指数表各龄阶各立地指数级的树高值，再分别按公式（20）～（22）计算χ2及误差值，结果见表7和表8。从表中可以看出，单形和多形立地指数的χ2值分别为0.01～0.93 和0.03～0.41，均小于χ20.05值（14.07），2 种立地指数表均通过显著性检验。

单形立地指数表在估测误差检验中（表7），立地指数估测误差Si介于0.10～1.47，在立地指数级10、12、14、16 时Si值较低，而在立地指数18 和22 时分别接近和超过1 m；不同龄阶的估测误差Sz在0.45～1.27，呈现低龄阶与高龄阶偏大而中间龄阶较小的趋势，且误差值在6～8 龄阶和20 龄阶的Sz均超过1 m，表明单形立地指数表在较高立地指数级，以及较低、高龄阶均不能达到较高的预测精度。

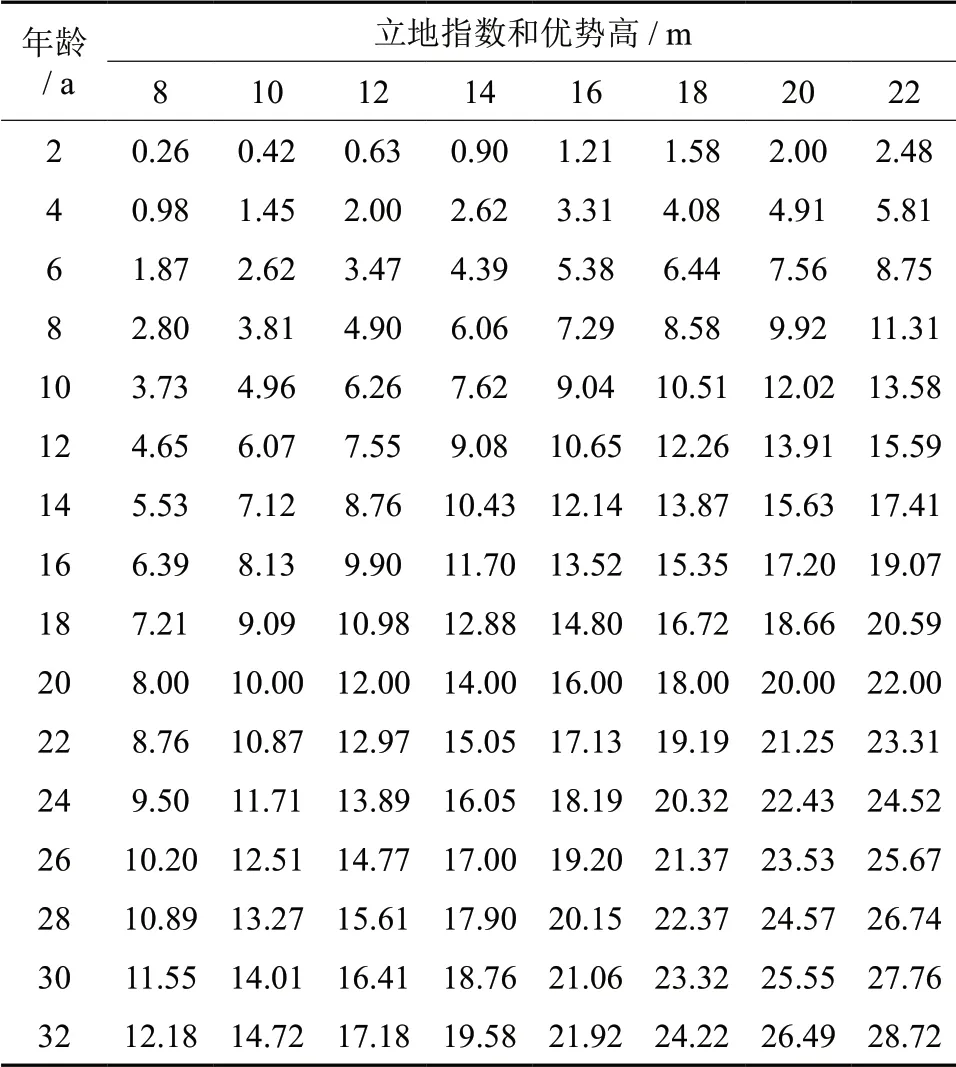
表6 湖北杉木多形立地指数表Table6 Chinese fir polymorphic site index table in Hubei province

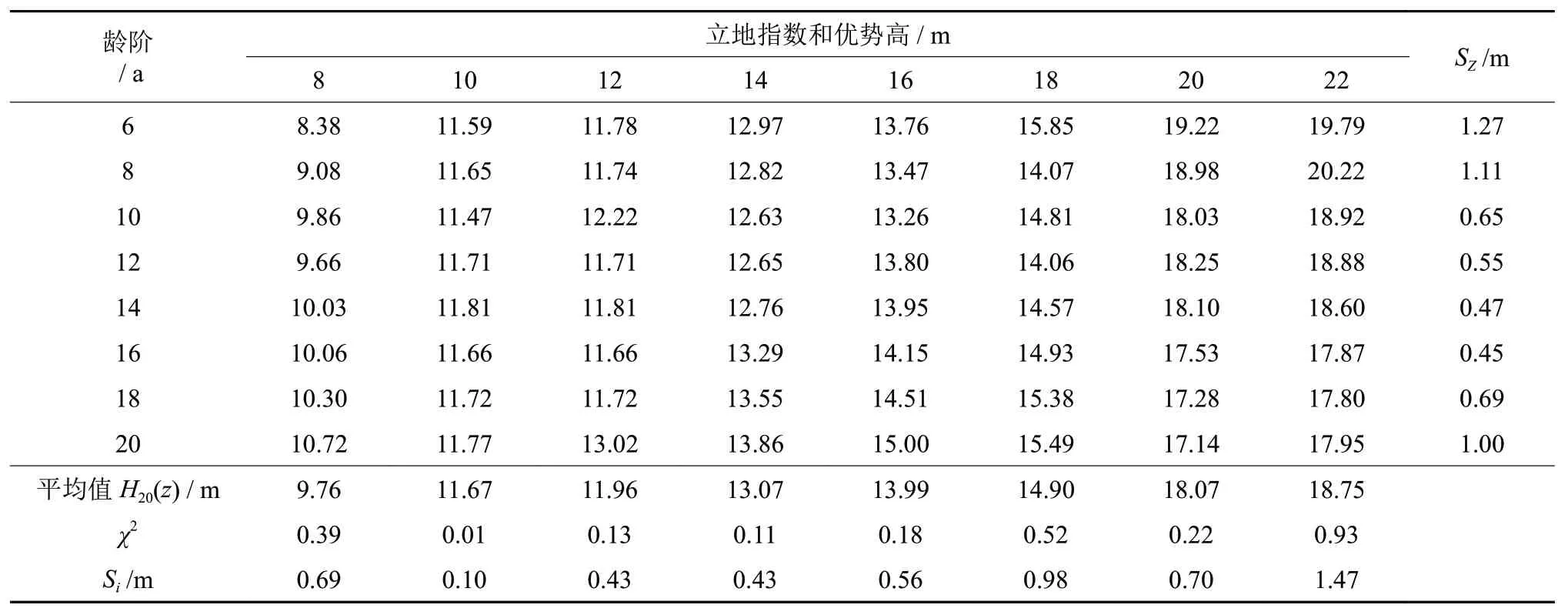
表7 单形立地指数序列及其检验Table7 Simplex site index series and its test

多形立地指数表的检验结果表明（表8），立地指数估测误差Si介于0.22～0.95，不同龄阶估测误差Sz在0.43～0.98，均仅在较高立地指数级和较高龄阶出现较大误差值，但均未超过1 m，达到了较好的预测效果。

通过以上分析表明，尽管单形和多形立地指数表均满足显著性检验，但从预测精度来看，单形立地指数表有12.5%的立地指数级和37.5%的龄阶误差查过1 m，而多形立地指数表则均无大于1 m 的误差，多形立地指数表具备更好的适应性和更高的预估精度。

3 结论与讨论

1）分别以7 种理论方程及其中的5 个理论方程的差分方程为基础方程构建湖北省杉木人工林优势高生长模型，利用拟合参数AMR、RMSE 以及R2等指标进行检验，结果表明理查德（Richards）理论方程和以c 为自由参数的理查德差分方程的拟合效果最优。从各方程的拟合优度、参数估计、误差检验和残差分析表明，差分方程的拟合效果均优于理论方程，与段爱国[15]研究得出的差分方程拟合精度高、表现更优，郑勇平[20]研究认为多形地位指数曲线模型明显优越于单形地位指数曲线模型的研究结论一致。本研究中Richards、Weibull 的2 参数方程拟合精度高于对应的3 参数方程，与段爱国[15]的研究结果一致；基础方程相同时，以b 或c 为自由参数的差分方程的拟合结果要优于以a 为自由参数的差分方程，这与相聪伟[21]的研究结果一致。

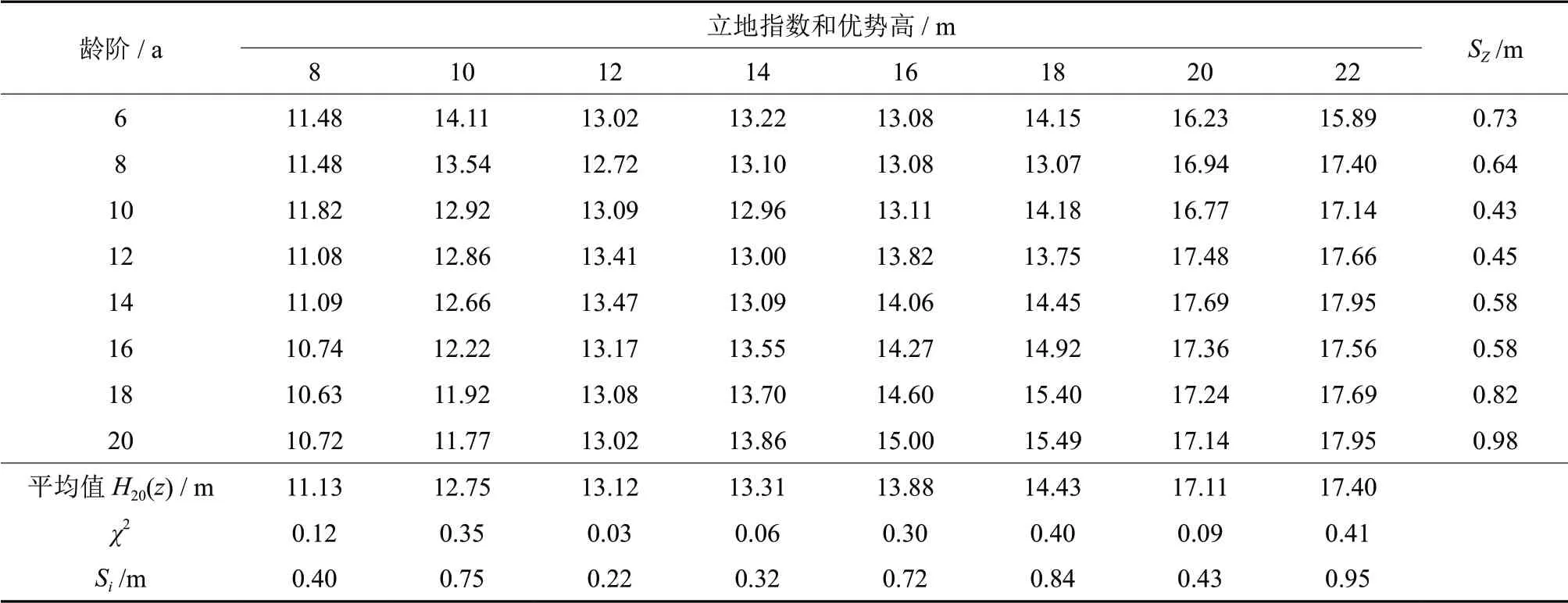
表8 多形立地指数序列及其检验Table8 Polymorphic site index series and its test

2）以20 a 为基准年龄，2 m 为级距，8 个立地指数级（8～22 m），分别选择理查德理论方程和考尔夫差分方程为基础方程，采用相应的导向曲线法和差分法编制单形与多形立地指数表，经χ2检验两种立地指数表均通过了显著性检验，达到了编制立地指数表的要求，但单形立地指数表预测精度检验的误差值Si、Sz并不太理想，分别在较大指数级和低、高龄阶的误差值超过了1 m，导致立地指数预测精度较低，适用范围较小，而多形立地指数表的误差值Si、Sz均未超过1 m，预测精度明显高于单形立地指数表。结果与张伟[13]、杨传强[22]、刘财富[23]、刘发林[24]等的研究结论一致，均表明多形模型能更高精度地拟合实际生长过程，多形立地指数表精度更高，适应性更强，对立地质量评价更可靠。

3）本研究使用所编立地指数表对全部92 块杉木人工林标准地立地质量进行评价，结果表明单形和多形立地指数表分别有9.8%和7.6%的标准地立地质量处于较差水平（立地质量8、10 m）；68.5%和65.2%的标准地立地质量处于中等水平（立地质量12、14、16 m）；21.7%和27.2%的标准地立地质量处于较高水平（立地质量18、20 m）。两种方法所编制的立地指数表的立地质量评价结果基本一致，符合湖北杉木北缘产区立地质量的实际现状。对比中等立地质量时湖北杉木人工林胸径（12.6～16.7 cm），要略低于《杉木速生丰产林标准》（2007）中北缘产区杉木人工林同等立地质量下的杉木胸径（13.8～17.3 cm），这可能与建模数据中高龄阶优势木样本量不充足有关；略低于《贵州省杉木速生丰产林标准》中对应的胸径值，符合实际生长状况。

4）本研究利用单株优势木与林分年龄数据编制湖北杉木人工林立地指数表，能客观反映湖北杉木人工林立地质量，但在我国森林资源清查中往往没有优势木树高的直接记录，需要利用平均木与优势木的关系来间接获取优势木信息，因此，接下来将利用3 株平均木数据来进一步验证研究结果。