基于核心素养下“本真数学”的课堂实践
出更新
【摘要】小学数学教学中,情境创设要体现数学味道、探究活动要突出数学思考、练习设计要关注知识内在本质、总结反思要提炼数学思想方法.要让学生在数学学习中理解数学概念的内涵,把握数学知识的内在本质和联系,揭示数学规律的形成过程,感悟数学特有的思维方式,追求数学理性精神,促进数学核心素养的培养.
【关键词】本真数学;核心素养;课堂教学;实践策略
【基金项目】本文为教育部福建师范大学基础教育课程研究中心2017年开放课题《小学本真数学课堂的研究》(K课题编号:C—2017046)成果论文.
所谓“本真数学”,就是要从数学的学科本质出发,准确把握数学的性质,遵循了数学学习的规律,提高学生的数学素养.《小学数学课堂的有效教学》一书对数学学科本质做了如下的归纳:“对基本数学概念的理解、对数学思想方法的把握、对数学特有思维方式的感悟、对数学美的鉴赏、对数学精神(理性精神与探究精神)的追求”.如何基于学生发展核心素养、基于儿童需要,让数学回归本真,以数学本真之美提升学生数学素养呢?
一、情境创设要体现数学味道
《数学课程标准》指出,数学教学应从学生的生活经验和已有的知识背景出发,创设有效的教学情境以激发学生的学习兴趣,为学生提供良好的学习数学的环境,引导学生在自主探究的过程中理解和掌握基本的数学知识和技能、培养数学思维能力、感悟数学思想方法,同时获得广泛的数学体验.因此,在教学中,要创设有“数学味”的情境,充分运用直观的方法,让抽象的数学知识成为学生常见的生活原型,成为学生能亲身体验的东西,这样可以给学生探索的方向,能使学生产生一种熟悉感、亲切感,有利于帮助学生理解数学知识,提炼数学知识的本质属性.
如,教学“买文具(认识人民币)”一课,创设了如下的情境:
师:今天是笑笑妈妈的生日,她想买一枝花(1元)送给妈妈,她拿出一张人民币(1角钱),你猜售货员阿姨会卖给她吗?为什么?(课件演示)
生1:不会,因为她的钱不够.
生2:她把1角钱当作1元了.
师:你能教教笑笑怎样认识人民币吗?
对人民币的认识,学生有一定的生活经验,创设这样的教学情境,符合一年级学生的年龄特征,能有效地促进学生“快乐、有效”的学习,而“教教笑笑怎样认识人民币”就是本节课的知识目标.因此,所创设的情境应是回归“数学本真”的情境,是基于学生已有经验、有助于学生实现生活经验数学化的情境,是为数学教学的“生活化”及生活问题的“数学化”提供可能的情境.学生认识了人民币之后,教师又创设了一个“超市购物”的模拟情境,让学生扮演售货员、顾客,进行学习用品的买卖,让学生体验到用学过的知识解决生活中的问题.这样的数学情境以亲历生活体验为出发点,以回归生活应用为落脚点,能有效促进学生的学习.
二、探究活动要突出数学思考
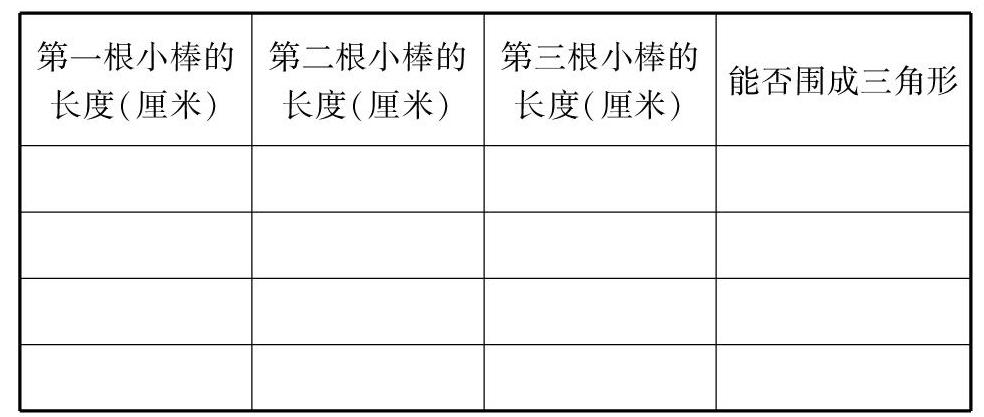
数学思考是数学教学的核心,《数学课程标准》将“数学思考”作为小学生数学学习的四大目标之一,离开了思考谈数学教学,就会使数学教学成为无源之水,无本之木.教学过程中,教师要引导学生有效参与数学活动,经历学习的全过程,在探究活动中发现问题,思考并解决问题.如教学“三角形三边关系”时,我为学生提供了学习材料:四根小棒(10厘米、6厘米、5厘米、4厘米),一张表格,让学生分组探索三角形三边的关系.
第一根小棒的长度(厘米)第二根小棒的长度(厘米)第三根小棒的长度(厘米)能否围成三角形
1.动手操作:小组合作任选三根小棒围成一个三角形,把结果填写在表格里.
2.探究思考:(1)为什么选10厘米、6厘米、5厘米和6厘米、5厘米、4厘米能围成三角形?
(2)为什么选10厘米、6厘米、4厘米和10厘米、5厘米、4厘米不能围成三角形?
3.分析发现:(1)6+5>10,4+5>6,能圍成三角形.
(2)6+4=10,4+5<10,不能围成三角形.
4.举例验证:另外找三根小棒围一围,验证自己的发现.
得出:两根小棒长度之和大于第三根小棒时,才能围成三角形.
5.引申问题:三角形三条边有怎样的关系?
6.得出结论:三角形两条边长度之和大于第三边.
教学中,教师引导学生经历了探究活动的全过程,层层深入,通过“操作—思考—发现—验证—思考—归纳”,不断地在活动中进行数学思考,学生学到的不仅是数学知识,还有数学思想和方法,落实了教学目标,提高了数学学习能力.
三、练习设计要关注知识内在本质
数学是一门具有严密逻辑性的科学,数学知识之间有着紧密的联系,教师在教学完新知识后,要设计练习帮助学生巩固新知识,深刻地理解知识间的内在本质和联系,拓展学生的解题思路,提高学生分析问题和解决问题的能力,发展学生智力.因此,练习要根据知识的结构特征、学生的认知规律以及课程标准的要求精心设计,要有“内涵”、有“坡度”、有“智慧挑战”,要遵循由易及难,由简到繁,由基本到拓展的发展顺序去安排,让不同水平的学生都练有所得.
如“平行四边形面积”一课,学生探讨出计算方法之后,我设计了以下的练习:
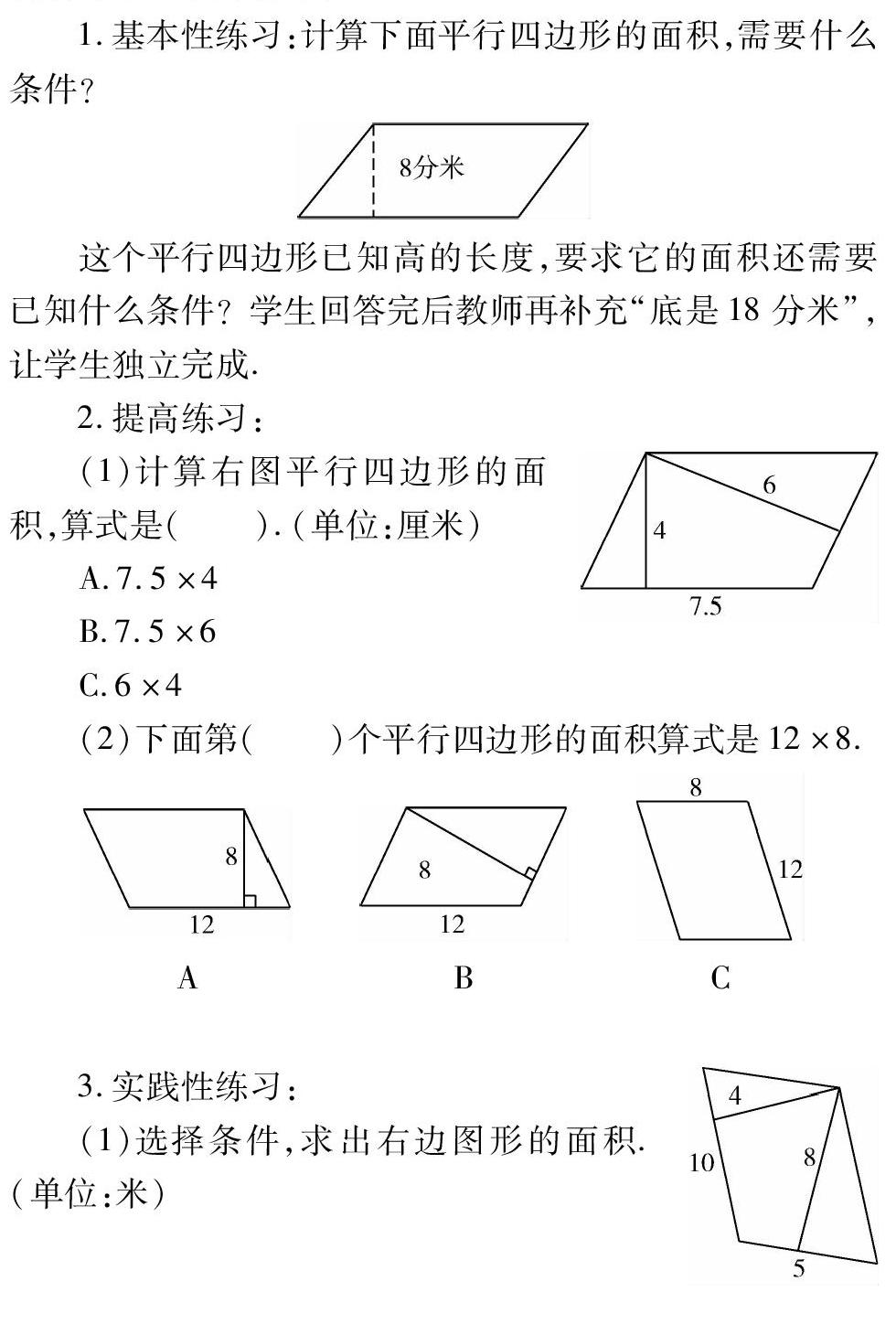
1.基本性练习:计算下面平行四边形的面积,需要什么条件?
这个平行四边形已知高的长度,要求它的面积还需要已知什么条件?学生回答完后教师再补充“底是18分米”,让学生独立完成.
2.提高练习:
(1)计算右图平行四边形的面积,算式是().(单位:厘米)
(2)下面第()个平行四边形的面积算式是12×8.
3.实践性练习:
(1)选择条件,求出右边图形的面积.(单位:米)
本组练习设计由浅入深,分层训练,逐步形成技能.基本练习在于检查学生是否会运用公式计算平行四边形的面积,加深对公式的巩固.提高练习是让学生明确计算平行四边形面积要选择正确的“底”和“高”.实践练习在于让学生能运用所学的知识解决生活当中的实际问题,培养学生的实践能力.发展性练习目的在于帮助学生深化知识、扩展知识,沟通知识间的内在联系,发展学生思维的广度和深度,培养学生创新的精神.
四、总结反思要提炼数学思想方法
数学思想方法是处理数学问题的指导思想和基本策略,是数学学习的灵魂,是学生数学素养的核心.刘云章教授认为:“重视对数学思想方法的领悟将能唤起数学学习者潜在的数学天赋,提高其数学素养,从而提高学习效益和质量”.数学思想方法的获得,一方面,需要教师进行有意识的渗透和培养,另一方面,也要靠学生的“悟”——在自身总结反思中提炼.例如,在“平面图形的面积复习”教学中,教师可引导学生思考:平行四边形、三角形、梯形的面积公式是怎样推导的?有什么共同点?学生在总结反思中理解了“转化”的数学思想方法.如学生学习完“三角形内角和”时,我让学生回顾学习过程:先计算直角三角形、等边三角形的内角和度数,再用猜测、操作、验证等方法推导一般三角形的内角和,最后归纳得出所有三角形的内角和为180度.学生回顾思维过程中总结出“归纳”的思想方法.因此,当数学学习结束后,教师要引导学生回顾自己的思维活动,总结反思自己是怎样发现和解决问题的,运用了哪些基本的思想方法等,及时对所应用的数学思想方法进行概括与提炼,从数学思想方法的高度把握知识的本质,提升课堂教学的价值.
“本真数学”课堂教学,主张以“本”为核心,以“真”为重点,遵循“问题情境—探索活动—实践应用—反思提升”的教学程序,经历提出问题、分析问题、解决问题、应用问题的过程,探索数学本质,建构数学模型,提升数学素养.
【参考文献】
[1]刘加霞.小学数学课堂的有效教学[M].北京:北京师范大学出版,2008.
[2]陈桂香.小学数学课堂教学中应体现“数学味”[J].教师博览(科研版),2011(11):61.

