策略教学要让学生有“震撼感”

徐宏臻 陆兆芬

“解决问题的策略”是苏教版小学数学教材编写的一大特色。在教学实践中，笔者发现，要想让一种策略真正走进学生心里，使其能自觉地、主动地运用，必须让学生切实体悟这种策略的价值和作用，内心受到强烈的震撼，有过真切的情感体验。这样，学生才会体验深刻，才会由衷地喜爱、主动地亲近、认真地学习并自觉地运用这种策略。为此，在具体教学某种策略时，教师务必紧扣策略的本质，精心设计教学活动，以彰显这种策略的价值，凸显这种策略的内涵。如何让策略教学使学生产生“震撼感”呢？现以四年级下册的“画图的策略”为例，谈谈笔者的一些做法。

一、震撼于算理的“清”与“浑”

为了彰显某种策略的价值，苏教版小学数学教材在选择例题时是精心的，尤其是对例题难度系数的把握可谓“落入学生最近发展区”。例题过难，学生久攻不下，会挫伤积极性，从而产生畏难情绪，这不利于学生学习这种策略;例题过易，毫不费力就能解决，则学生不愿探寻是用何种策略去解决问题的，也不愿感悟这种策略的意义和内涵。为此，要选择那些既能凸显策略的价值和内涵，又有一定的挑战性，学生“跳一跳，能摘到桃子”的典型问题。这一问题须要借助某种独特的策略才能解决。这样，学生才会在解决问题后，主动反思用了何种策略，此策略的价值和作用是什么，如何运用等，才会在内心产生较强的自我体验。

苏教版小学数学教材在教学“画图的策略”时，编排的例题如图1。

在教学前，笔者不作任何提示，直接让学生解答此题，结果发现约一半以上的学生无师自通，他们的列式一般分为两种：一是“去多法”，即用72-12=60（枚），60÷2=30（枚），得到小宁的枚数，用30+12=42（枚），得到小春的枚数;二是“补少法”，即用72+12=84（枚），84÷2=42（枚），得到小春的枚数，用42-12=30（枚），得到小宁的枚数。较为典型的错例是：72÷2=36（枚），36-12=24（枚），得到小宁的枚数，36+12=48（枚），得到小春的枚数。针对此错例，笔者引导学生把得数带入原题进行检验，从而发现问题。还有少数学生无计可施。笔者让能正确解答的学生上台说理，发现有些学生说不清、道不明。有的学生即使自己说清了，但台下有许多同学听得似懂非懂。在笔者的“如何让别人一下子明白你的思路和理由”的启发下，有少数学生想到了画图，并借助画出的图讲清了自己的解答过程及其理由。此时，学生初步感悟到画图的好处：便于正确解题，便于说清解题思路和理由。

在“能正确解答”与“不能正确解答”，“能借助图说清解题思路和理由”与“不借助图就不能说清解题思路和理由”的现实对比中，学生强烈地感受到画图的价值，心灵受到一次震撼，对画图的好感悄然而生。

二、震撼于表征的“简”与“繁”

实践证明，要让学生切实体悟到某种策略的益处，真正掌握这种策略，需要有一定的方法作支撑，需要形成一定的操作技能。为使学生掌握画图技能，教师需要适当教学生一些用图描述问题的方法，且让其经常练习。为此，笔者在学生自主尝试画图的基础上，有目的地展示部分学生的作品，并让其他学生评议，看是否表示出题意，包括条件和问题是否规范、是否简明等。笔者还帮助学生修改和完善所画的图，使其规范和简明。为了教会学生画图的方法，笔者还示范画图，让学生清楚地看到如何把原题用图准确地、规范地、简明地表示出来，即看到文字是怎样变成图形的。如在画上述例题图时，可以先画两条不同的线段分别表示小宁和小春的邮票枚数，分别标上“小宁”和“小春”，两条线段的左端要对齐，以便比较，而表示小春的那条线段要画得稍长一些，还要在长的部分标上“多12枚”;再用大括号表示两人一共“72枚”;最后在两条线段上分别画出大括号，分别标上“？”，表示所求的问题。笔者示范后，让学生再次学画，或修改原先的图，直至画出符合要求的图。在此基础上，笔者引导学生图文对照，看着图说其所表示的意思，并与原题中的文字进行比较，看哪个更能清晰地、简明地表达题意，从而进一步感受图的好处，培养学生读图、识图的能力。笔者在引导学生把文字信息转变为图形语言，和把图形语言转变为文字信息的双向过程中，让学生通过对比，强烈地感受到图能够把抽象的文字变为形象的图形，从而使题意简明，数量关系清晰。

三、震撼于思路的“多”与“少”

在教学过程中，笔者发现，没有图时大多数学生往往只有一种解题思路，而借助图能触发多种解题思路。因为学生借助图能直观地分析数量关系，快速地找到解题思路，从而快捷地找到多种解题方法，并能在图上清楚地说明。其他学生則能边看图边听介绍，顺着这种思路想下去，从而很方便地理解这种思路。如大多数学生在解答例题时只想到“去多法”，如上所述。为了进一步凸显图的形象性和生动性，笔者变静为动，用剪刀当场剪去小春比小宁多的12枚。学生形象地看到这时总数也随之减少了12枚，两人变得同样多[图2（1）]。两人现在的总数是72-12=60（枚），再用60÷2=30（枚），从而得到小宁的枚数，要求小春原来的枚数，则需要把剪掉的“12枚”还回来，即用30+12=42（枚）。笔者还是引导学生借助检验，证明结果是正确的，从而说明这样思考是正确的。

受此启发，学生还想出了“补少法”，即先借来12枚给小宁，这时两人的枚数变得同样多[图2（2）]。这时，总数也增加了12枚，变成了72+12=84（枚），用84÷2=42（枚），从而得到小春的枚数，因为小宁是借来12枚才与小春同样多的，所以小宁还要把这12枚还回去，所以小宁的枚数是42-12=30（枚）。

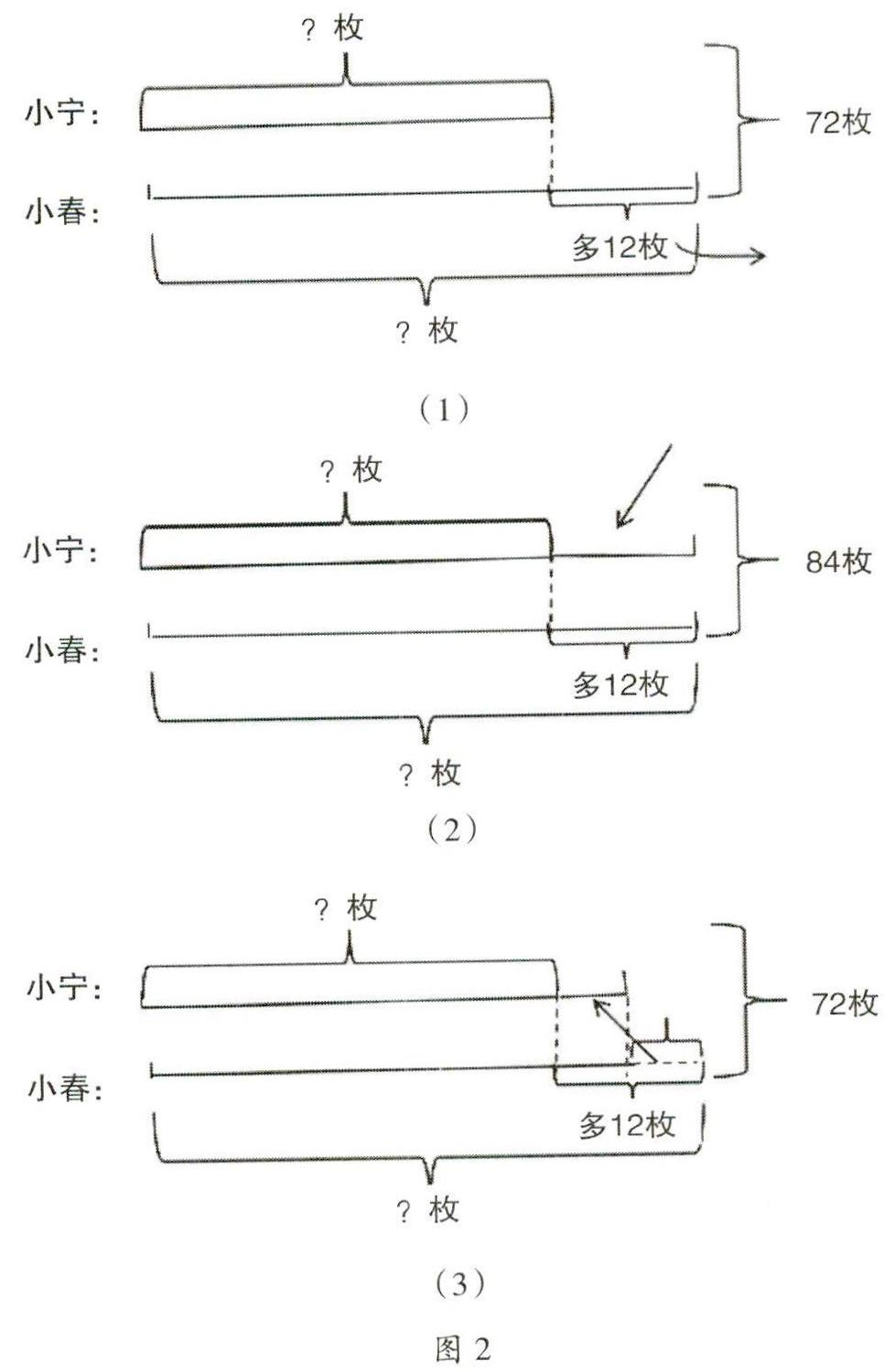
由于前两种思路都是设法让两人的枚数由不相等变成相等的，受此启发，有学生想到了“均分法”，即把小春比小宁多的12枚平均分成两份，把其中一份给小宁，这时两人又变得同样多，而这时两人的总数保持不变[图2（3）]。因此列式为72÷2=36（枚），得到两人现在每人的枚数，小宁要有借有还，于是用36-6=30（枚），得到小宁的枚数，小春则要把给小宁的6枚拿回来，所以小春的枚数是36+6=42（枚）。筆者有意把开始的错误列式72÷2=36（枚），36-12=24（枚），36+12=48（枚）与之进行对比，让学生看到开始思路的合理处和错误处，即小春不是把12枚给小宁，而是把6枚给小宁，这样两人才同样多，才好用72÷2=36（枚），从而得到两人现在的枚数。借助图可以清楚地说明这个道理。这样，既肯定了学生原先思路的合理性，保护了学生思考的积极性，又因势利导，巧妙地把学生引到正确的思路上来。

在三种思路一一呈现后，笔者还利用课件集中呈现，引导学生聚焦：它们虽然解法不同，但有什么相同的地方？学生发现：它们都是把原先不相等的数量变为相等的数量，都是用假设法使其相等的，都是把原先复杂的问题转化为简单的问题。

四、震撼于运用的“广”与“大”

苏教版小学数学教材在教过例题后，都要引导学生回顾曾经运用该策略解决过哪些问题，从策略的角度回顾和再现以前解决过的问题，以进一步感知该策略、内化该策略。笔者从一至四年级的教材中，有目的有意识地选取一些有代表性的例题，先一一出示，并让学生具体介绍当时是如何运用该策略的，再集中展示和回顾，让学生感受画图策略在各个阶段和各个领域的运用，以增强学生的感性认识，丰富学生的自身体验，使其切实体会到这一策略运用的“广”与“大”，心里产生更多的体验。

此外，还要让学生在运用中进一步增强策略体验，把握策略内涵，形成运用意识。笔者引导学生从模仿性的初步运用，到自主性的综合运用，再到创造性的灵活运用，引导学生拾级而上，逐步提升，从简单运用到复杂运用，从相差关系到倍比关系，从提供半成品的图让其画完，到引导其独立画图，最后到在脑中画图。

这里的“广”与“大”还指作用多。如借助图进行检验，因为在实际教学中，笔者发现，有些学生还没有学会如何检验。其实，如果依据题意画对了图，只要引导学生把图中的问题与条件相互交换，看能否由此及彼，相互推导即可。可借助图写答句，因为学生在写答句时，经常张冠李戴，只要引导其看图写答句就不会混淆。

当然，仅靠几节课就让学生形成画图意识和能力，显然不可能，教师还要在今后的教学中让学生不断地、真切地体会到画图的独特价值和神奇功效，并鼓励其积极地尝试运用，以便逐步形成“爱画图”“会画图”“常画图”的思维习惯，最终形成几何直观的意识。

总之，在策略教学中，教师务必始终关注策略二字，紧扣策略的内涵进行教学设计，重视学生对策略的感悟，让学生获得强烈的、准确的、深刻的和丰富的感受，务必重视策略的运用，让学生经常地、反复地运用，在运用中不断地增强体验、深化认识。

[责任编辑：陈国庆]