高中生物理学习兴趣量表测题典型性专家调查

李建彬 胡象岭 王德才

摘   要：采用德尔菲法评估了高中生物理学习兴趣量表测题的典型性。综合专家工作单位、职称和工龄三个因素，筛选了27名从事物理教育研究或中学物理教学实践工作的专家，对其开展了两轮调查，并统计了专家意见的集中程度和协调程度。调查结果显示，兴趣水平量表中的43项测题中有41项测题的典型性得到了专家的认可，有2项测题典型性评级较低，予以删除。

关键词：物理学习兴趣;量表修订;专家调查法;德尔菲法

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2019）5-0073-4

1    引  言

物理学习兴趣一直是物理教育领域备受关注的话题。为了评价中学生物理学习兴趣水平，胡象岭等编制了物理学习兴趣量表并进行了多次修订[1-6]。该量表为自陈式量表，与一些调查工具要求被试直接给出对物理学习是否感兴趣或感兴趣的程度不同，该量表各测试题目（实为一个陈述句）描述的是学生对物理感兴趣或不感兴趣的典型行为和特征，通过被试在这些测题上的自我评价，来判断其物理学习兴趣水平。因此，量表中各测题所描述的行为、特征是否典型，是影响量表效度的关键。评估测题的典型性需要采用多种方法，专家评估便是其中重要的一种。此前对该量表进行专家评估时采用的是质询专家、与相关人员座谈等形式。这在一定程度上提高了测题的典型性，但这种“面对面”的方式往往会使评估人受到他人的干扰，不能很好地整合所有专家的观点。德尔菲法（Delphi Method）要求专家“背对背”地给出意见，避免了上述方式中的不足。因此，本次高中生物理学习兴趣量表的修订，我们采用了这一方法来检验测题的典型性。

2    研究方法

2.1    德尔菲法

德尔菲法起源于美国，是一种利用函询形式，按照规定程序征求專家意见的方法。使用该方法时，研究者首先确定评估目标，然后根据研究所需要的知识范围选聘专家，并向专家发布所要征询的问题及相关要求和背景资料等材料。专家独立作出书面回答，提出意见并说明依据，直接提交给研究者。研究者统计整理收集到的专家意见，并将统计结果反馈给各位专家，反馈时不透露发表意见专家的信息。专家参考上一轮调查结果及相关材料，对自己的意见进行调整并说明依据和理由，再次交由研究者统计、分析和反馈。如此反复多次，直至所有专家不再改变意见或各专家的意见趋于一致，结束调查，得到最终评估结果。从实施过程看，德尔菲法具有匿名性、反馈性、统计性等特点，充分发挥了信息反馈和信息控制的作用[7]。因此，该方法尤其适用于信息分析、评估与预测，在各领域都有广泛应用。

2.2    专家的选择

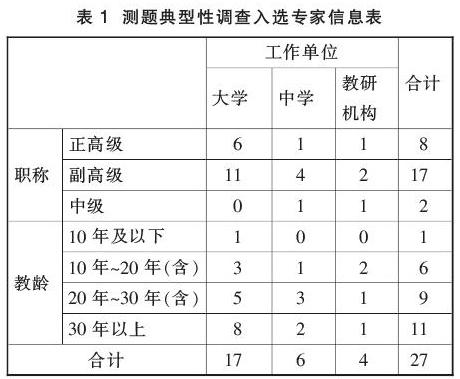
选择合适的专家是应用德尔菲法的关键。本研究旨在评估高中生物理学习兴趣量表测题表述的典型性，因此专家应在从事中学物理教育研究或中学物理教学实践工作的人员中选聘。在筛选专家时主要考虑了专家的工作单位、职称和工龄三个因素。具体条件是：专家应在大学、中学或教研机构工作;专家职称不低于中级，以高级职称为主;专家工龄原则上不低于10年，如遇特殊情况可适当放宽年限。基于这些条件，本次调查共选择了27名专家，专家信息如表1。

2.3     征询方法

在开始专家调查之前，本研究在2006年版高中生物理学习兴趣量表[4]的基础上，修订了量表的部分测题表述，形成了修订后的高中生物理学习兴趣量表初稿。该量表包括兴趣水平量表、测谎量表和效度测题三部分，本次向专家征询的是兴趣水平量表中所有43项测题的典型性。征询专家意见时，研究者编制专家问卷，通过电子邮件向27名专家进行了两轮咨询，问卷回收率均为100%。第一轮专家问卷向专家提供了研究背景和调查目的，列出了需要评估的所有测题，并在其后给出了7个典型性等级选项，即“非常不典型”“很不典型”“较不典型”“一般”“较典型”“很典型”“非常典型”，分别用整数分1～7分来表示。调查时要求专家评估每项测题的典型性，并请专家提出意见。第二轮调查问卷向专家报告了第一轮调查的统计结果，同时在每项测题后列出专家赋分情况的统计数据，要求专家参考第一轮调查结果再次评定每项测题的典型性，典型性等级划分与第一轮调查相同。

3    调查结果

3.1    第一轮调查

专家意见的集中程度和协调（一致）程度是本次专家调查重点关注的两个方面。为了描述第一轮调查得到的专家意见的集中程度，计算了每项测题典型性得分的均值（M）、标准差（s）、极值、中位数、众数、低分比率、满分比率。其中，“低分比率”表示将某测题的典型性评定为4分及以下（典型性等级为“中等”和“不典型”）的专家占总专家数的比例;“满分比率”表示将该测题典型性评定为7分，即“非常典型”的专家占总专家数的比例。专家意见的协调程度可以从两个方面来考查。一是专家意见在每项测题上的协调程度，可以用变异系数来表示，该系数可由某项测题得分的标准差s，除以均值M得到。二是专家意见在整个量表上的协调程度，可以用肯德尔和谐系数（W）来表征。W介于0到1之间，W=1，表示专家的评定结果完全一致;W=0，表示完全不一致。

均值是专家意见集中程度的重要体现。在第一轮调查中，典型性评定均值最小的是第11题，为4.77，最高的是第23题，为6.48。从专家评定的均值看，没有测题的典型性落在“不典型”的等级区间。为了更好地分析第一轮专家调查的结果，按照均值大小对43项测题进行分类。以等级分值“5”“6”为界点，将专家评定后的测题分为“高典型性”“中典型性”和“低典型性”三类，如表2。

由表2可见，中典型性的测题最多，达到了26项，其次是高典型性的测题，有13项。整体上看，专家对本次修订后的量表测题的典型性评定较高，但仍有4项测题的均值低于5，典型性较低。同时，除了专家在高典型性的13项测题上意见较为一致外，在其他测题上均出现了不同程度的分歧。使用SPSS 23计算了第一轮调查的肯德尔和谐系数，W=0.140（χ2=123.808，P<0.001）。一般认为，肯德尔和谐系数W达到0.7左右表明专家意见共识度较为理想[8]。当协调系数较小时，应当分析原因，查看是否存在专家组之间的意见不一致情况[9]。为此，本研究按照工作单位将专家划分为三组，比较了三个专家组的评定情况，结果如表3。

由表3可见，大学专家组在本次评定中的整体均值最低，其次是教研机构专家组，中学专家组的整体均值最高。中学专家组是唯一整体均值超过6分的专家组，给出的最大均值和最小均值也都大于其他两组专家。从测题均值分布来看，中学专家组评定中均值大于6的测题达到了36项，没有均值低于5的测题;而大学专家组则较为严格，均值大于6的测题数仅为7项，均值小于5的则有6项，大部分测题的均值分布在5和6之间;教研机构专家组中均值大于6的测题相较于大学专家组要多，有21项，但均值小于5的测题则达到了8项。

对于低典型性的测题，三个专家组的意见也不太一致。在均值小于5的测题中，大学专家组与教研机构专家组重合的测题仅有3项。如果把中学专家组中均值低于6的测题视为典型性不高的项目的话，同时被三个专家组评判为典型性不够高的测题仅有一项，为测题中的第11题。

从第一轮调查中可以看出，专家对于测题的典型性评定既有意见一致之处，又存在一定程度的差别。从专家的工作背景看，大学和教研机构的专家对测题的要求较为严格，而中学专家相对宽松。

3.2    第二轮调查

第二轮专家调查的数据处理与第一轮相同。同样以均值作为划分依据，统计了第二轮专家调查中三类测题的数量，并与第一轮调查结果进行对比，如图1。

经过第二轮调查专家重新评估，高典型性的测题由13项增加到了19项;中典型性的测题由26项减为22项;低典型性的测题由4项减为2项。

使用SPSS 23计算了第二轮专家调查的肯德尔和谐系数，W=0.303（χ2=343.630，P<0.001），达到了具有一般一致性的水平，相较第一轮的0.140有所提高，表明专家意见趋于集中。两轮调查中和谐系数的χ2检验P值均小于0.001，表明两次调查的结果可取。但第二轮调查的肯德尔和谐系数相较于理想值仍然偏低，这可能与专家组间的差异有关。分别计算了两轮调查中三个专家组内部的肯德尔和谐系数，并对比了两次调查中专家组的评定情况，如表4和图2。

从表4可以看出，经过第二轮调查，各专家组内部具有了更高的一致性。由图2，相较于第一轮调查，变化最大的是大学专家，主要变化在于高典型性测题占比增加，而中典型性和低典型性测题占比降低。三类测题的占比情况在中学专家组和教研机构专家组中变化不大。由此可以推断，各位专家的意见已基本保持不变，同时考虑到调查成本，本研究接受第二轮专家调查结果，终止调查。

3.3    测题的筛选

调查结束后即要根据专家意见对测题作出筛选，删除专家认为不够典型的测题。这就涉及到筛选测题判据的问题。本研究采用界值法[7]筛选测题。筛选时关注了3个数据指标，即每项测题的均值、满分频率和变异系数。界值的计算方法如下：均值（或满分频率）的界值等于各项测题均值（或满分频率）的算术平均数减去其标准差，高于界值的入选。变异系数的界值等于各项测题的变异系数均值加、减其标准差，位于两界值中间的入选。之所以计算了两个变异系数的界值，是因为对于典型性差的项目，专家意见可能出现两种情况：一是专家一致认为该测题典型性低，此时变异系数较小;二是专家对该测题的意见分歧很大，此时变异系数较大，这两种情况都是不被接受的。根据第二轮专家调查结果，计算了3个数据指标的界值，如表5。

为了避免误删，只有测题的3个数据指标均不符合入选要求时才被删除。经过筛选，本研究43项测题中，有2项测题被删除。对于有2个或1个指标不符合要求的测题，参考专家意见，经过讨论予以保留。

4    结  语

本研究采用德尔菲法，对高中生物理学习兴趣量表测题的典型性进行了专家评定。经过两轮调查，删除了专家评定中典型性低的2项测题。从专家调查结果看，两轮调查中，专家间的协调程度都不够高，表明专家对量表测题的典型性存在分歧，需要在后续研究中参考专家意见进一步修订。需要注意的是，本调查在德尔菲法的使用上只具有参考价值。如调查中只是要求专家对预先设计好的表述进行典型性评判，与经典的德尔菲法[10]要求存在一定差距;专家的判断依据及其信息来源、对问题的熟悉程度和權威程度对调查结果也有重要影响[7，11]，本研究也未对这些问题加以深究。另外，目前德尔菲法在应用过程中尚存在诸多问题[9]，德尔菲法本身存在一定的参考点效应和证实性偏差[11]，会影响专家对问题的评判，仍有待进一步研究完善。

参考文献：

[1]胡象岭.物理学习兴趣量表的设计与试测[J].课程·教材·教法，1996，16（2）：13，30-32.

[2]胡象岭，李新乡，林国强.物理学习兴趣量表的设计与分析[J].物理教师，1998，19（5）：1-5.

[3]高光珍，胡象岭，刘生庆.中学生物理学习兴趣量表的修订与检验[J].物理教学探讨，2004，22（12）：16-18.

[4]高光珍.高中生物理学习兴趣量表的编制与应用[D].曲阜：曲阜师范大学硕士学位论文，2006.

[5]胡象岭，杨昭宁，高光珍. 曲阜市高中学生物理学习兴趣调查[J]. 课程·教材·教法，2010，30（4）：72-78.

[6]李建彬.高中生物理学习兴趣量表的修订与应用[D].曲阜：曲阜师范大学硕士学位论文，2017.

[7]王春枝，斯琴.德尔菲法中的数据统计处理方法及其应用研究[J].内蒙古财经学院学报（综合版），2011，9（4）：92-96.

[8]SIEGEL S， CASTELLAN N J JR. Non-parametric statistics for the behavioral sciences [M]. New York： Mc Graw-Hill，1988.

[9]曾照云，程晓康.德尔菲法应用研究中存在的问题分析——基于38种CSSCI（2014-2015）来源期刊[J].图书情报工作，2016，60（16）：116-120.

[10]袁志彬，任中保.德尔菲法在技术预见中的应用与思考[J].科技管理研究，2006（10）：217-219.

[11]张冬梅，曾忠禄.德尔菲法技术预见的缺陷及导因分析：行为经济学分析视角[J].情报理论与实践，2009，32（8）：24-27.

（栏目编辑    李富强）