挖掘问题本质，凸显问题价值

吴静

[摘  要] 问题是思维的源泉，教师在课堂教学过程中，问题可以巧妙地引领学生的思考方向，启发学生的思维路径，还可以启发學生注重解题方法的总结与分析，引领学生将方法转变成思想，将思想积淀为能力，将能力转变为素养. 为此，笔者在常态的课堂教学过程中，一直关注问题的本质，以此凸显问题的价值，在问题的深入研究与实践中，促发教学目标的水到渠成，也触发学生学习能力的提升.

[关键词] 问题;本质;价值;初中数学

数学是一门以问题为主的学科，数学教学的目标之一是提高学生解决问题的能力，在教学过程中，教师对问题的斟酌、研讨是每天必备的，对问题的选择是教学准备的一项重要内容. 在教学中，究竟什么样的问题才是“好”的问题呢？对此，贝克浩斯（Backhouse）曾给出过这样一个说法：“最好的问题是那些来自于学生经验并由学生提出的问题. ”笔者作为初中数学教师，以此为理论依据，经过思考，结合实践，认为好问题应该具备如下几个特征：

源于生活，能激发学生的学习兴趣

数学本就来源于生活，同时也服务于生活. 初中数学与小学数学相比少了点“趣味”，增加了难度，抽象问题逐渐增多，使得部分学生对数学的兴趣减弱. 针对这种情况，教师可以在对问题的设置时联系实际，使教学的客观要求与学生的原有知识经验产生矛盾，这样的问题是能有效激发学生的兴趣和探究欲望的.

如“有理数的加法”是有理数计算的起始节，对于引入了负数的加法，学生会感觉有点抽象，直接用数学问题来归纳计算法则效果不佳. 为了使引入了负数后的加法更加“接地气”，可以选取与生活有关的问题引入：

（1）小明有个存钱罐，里面原有78元，今天小明去参加社会实践活动卖报纸，他将挣的13元又放进了存钱罐里，现在他共有多少元？

（2）小莉是个喜欢乱花钱的孩子，零花钱从来没有剩余，在欠了同桌25元之后又问别的同学借了10元买零食，问她现在实际总共欠多少元？

（3）小莉深受小明的感染，决定改掉乱花钱的习惯，于是她将家里的空饮料瓶卖了，卖到41元，之前她还欠同学35元，如果还掉后身边共有多少元？

（4）如果小莉卖饮料瓶得到41元，但是欠同学45元，她还得清吗？为什么？

通过上述四个问题可以引起学生的兴趣，引导学生用有理数的加法来解答，再进一步归纳有理数的加法法则，让学生感受实际问题到数学问题的自然过渡，其效果优于纯数学问题. 兴趣是最好的老师，如何有效激发学生的兴趣是教师在进行教学准备时首需考虑的，以源于生活的问题来激发学生的兴趣是有效途径之一.

难度适宜，能提高学生的解题能力

问题的难度是问题的基本属性，也是衡量一个问题是否是一个“好”问题的重要标准. 问题的难度要适宜，既要考虑学生的实际水平，让学生有探究的欲望，又要使题目具有挑战性，能提高学生的解题能力. 苏联心理学家维果茨基提出过要将问题的难度置于学生的“最近发展区”，及让学生通过一定的努力之后可以解决，这样既能激发学生的解决问题动机的同时使学生在解决问题之后产生成就感，进一步增加学习的兴趣.

如“相似三角形的判定（二）”是在学生已掌握了“由平行得相似”的基础上对“三边对应成比例的两个三角形相似”的探索. 在讲授过程中，直接告知学生判定定理则不利于学生对知识的真正理解，让学生自己探究证明该定理则难度太大，因此我们可以在教学中设计如下问题：

如图1所示，已知在△ABC和△A′B′C′中，==. 求证：△ABC∽△A′B′C′.

（1）除了定义外，还有什么方法可以证明三角形相似？

（2）如何把两个三角形转化到一个三角形内，利用平行线证明三角形相似？

（3）能否构造△A′DE，使其与△A′B′C′相似？

（4）根据已知条件△ABC与△A′DE是否全等？

（5）尝试给出定理的证明过程.

以上几个问题有针对性、有梯度，符合学生对问题的认知规律，可以帮助学生梳理解决问题的一般思路，同时这些问题也具有一定的挑战性，可以提高学生分析问题、解决问题的能力.

“一题多变”，能完善学生的知识体系

数学是一门前后联系性较强的学科，数学知识具备完整性. 好的数学问题常常能够“一问多变”，每“变”一次就要扩充解答此问的知识点，使该问题的容量增大，在解决问题的同时让学生学会知识的融会贯通，完善其知识体系.

如“若抛物线y=ax2+2x+1与x轴有公共点，求x的取值范围”是“二次函数与一元二次方程”中的一个典型例题，令Δ>0，即可算出x的取值范围，难度不大，学生可以自行解决. 在这个基础上教师可以变题：

变1：若函数y=ax2+2x+1的图形与x轴有公共点，求x的取值范围.

变2：若抛物线y=ax2+2x+1与x轴只有一个公共点，求x的取值范围.

变3：若函数y=ax2+2x+1图像与x轴只有一个公共点，求x的取值范围.

这三个变式看似差异不大，但却是学生容易混淆的，在实际解决问题的过程中错误率较高. 变1需要考虑函数为一次函数的情况，变2只需令Δ=0即可，变3也需考虑函数为一次函数这种情况. 将这些问题依次罗列，让学生加以区分，从而厘清函数类型与交点个数的关系，避免类似的错误再次发生. 学生在解决问题的过程中“反复做、反复错”的现象一直存在，究其根源就是知识掌握不牢固，没有构建自己的知识体系，“一题多变”可以在一定程度上帮助学生完善知识体系.

“一题多解”，能扩充学生的思维空间

“一题多解”，就是从不同的角度对一个问题加以思考，探究出不同的解决方案. 让学生摆脱标准答案的“桎梏”，让学生有施展的空间，培养学生的发散思维. 因此，问题的设计要考虑它的可变性，根据题目的特征和学生的需要尽可能挖掘从不同角度去寻求解决问题的途径，以此来促进学生思维能力的提高[1]. 如“平行四边形”中的一道例题：

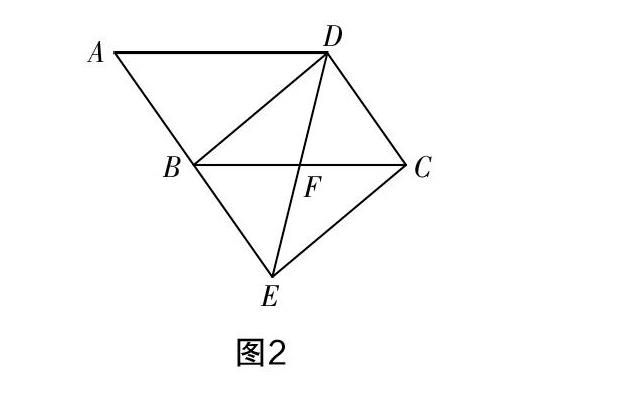
已知四边形ABCD是平行四边形，现将它的边AB延长到点E，使BE=AB，連接DE，交BC于点F，连接BD，CE，若∠BFD=2∠A，试判断四边形BECD的形状并证明.

法一：由四边形ABCD是平行四边形与BE=AB可证四边形BECD为平行四边形，根据∠BFD=2∠A，∠BFD=∠FDC+∠FCD可得∠FDC=∠FCD，因此FD=FC，DE=BC，所以平行四边形BECD为矩形.

法二：由四边形ABCD是平行四边形与BE=AB可证四边形BECD为平行四边形，根据∠BFD=2∠A，∠BFD=∠FBE+∠FEB可证∠A=∠DEB，则AD=ED. 再由BE=AB得BD是△ADE的高，因此∠DBE=90°，所以平行四边形BECD为矩形.

法三：由四边形ABCD是平行四边形与BE=AB可证四边形BECD为平行四边形，根据∠BFD=2∠A，∠BFD=∠FBE+∠FEB可证∠A=∠DEB，则AD=ED，因此ED=BC，所以平行四边形BECD为矩形.

以上三种方法从不同的角度，利用外角和内角的关系、等腰三角形“三线合一”、“等角对等边”得到所需的关系完成证明，引导学生去探索，从不同的角度思考问题，有利于学生发散思维的形成.

有开放性，能发展学生的创新能力

具备一定的开放性是“好”问题的重要标志. 它包含两个方面，一是问题的开放性，即问题来源的开放性，如问题具有一定的现实意义，与社会生活有着直接的联系;另一方面是答案的开放性，打破“一问一答”式的标准答案及“问题中所提供的条件都有用”的传统观念，这对于学生创新能力的发展有积极的作用. 如在“实际问题与一次函数（复习）”中，可自行设计或将现有题目改编成开放性问题：

已知甲、乙两地相距300 km，一辆货车与一辆轿车先后从甲地出发驶往乙地，如图3，线段OA表示货车离甲地的距离y（km）与时间x（h）之间的函数关系，折线BCDE表示轿车离甲地的距离y（km）与时间x（h）之间的函数关系.

（1）观察图像，你获取了哪些信息？

（2）你可以提出哪些问题供同学们求解？

该问题可以让学生组内合作、组间竞争，你问我答，形成一种活跃的课堂气氛，学生提的问题可能较为浅显，教师可以引导其深入挖掘信息，也可以补充部分问题[2]. 将这类开放性问题植入常态课教学，可以激发学生对问题的深究，发展学生的创造力.

数学教学的任何一个环节中都存在好的问题，没有好的问题就不具备创造性. 从教学实践来看，“好”的数学问题应符合学生的身心发展规律和知识接纳水平，能促进学生的思维发展与能力提高. 教师在教学中只有挖掘问题本质，方能凸显问题价值.

参考文献：

[1]蔡建新. 问题化学习，优化初中数学复习课教学[J]. 中学数学月刊，2018（10）.

[2]卫德彬，阮征，陈方勇，马遇青. 核心素养视域下的数学图形微课教学研究[J]. 中学数学教学，2018（6）.