用动态技术提高变式教学的效率——以等腰三角形的习题及其变式拓展为例

陈妮妮，潘春娥，唐剑岚

（广东省深圳市光明区马山头学校；百色学院；广西师范大学数学与统计学院）

数学变式教学是基于学生的经验起点和知识的逻辑生长点，对数学对象的非本质特征有梯度地、有广度地、有密度地、有深度地进行变式，以凸显数学对象的本质属性，进而把数学对象内化成科学的概念的教学，主要包括几何类变式、代数类变式和解题类变式.而动态数学技术是应用动态数学软件，诸如几何画板、Hawgent皓骏动态数学技术（以下简称“Hawgent皓骏”）、GeoGebra等，或平台改善数学教学的技术.恰当使用动态数学技术可以动态化、可视化、形象化变式教学中的“变”，从而提高变式教学的效率.文章尝试以等腰三角形一道习题及其变式拓展为例，在教学实践中以“例题—条件变—条件与结论同时变”的变式主线为明线，以“例题—形状变—位置变”的变式主线为暗线，融入Hawgent皓骏进行课堂教学探究，期待为提高变式教学的效率提供参考.

一、“闪”“色”结合，明晰解法的多重性

一题多解性变式的实质是以不同的论证方式反映条件和结论之间的必然本质联系.对于一题多解类题目，传统教学的处理方式相对生硬、呆板与滞后，其呈现的“静态”不利于打破学生定势思维的局限性.恰当使用Hawgent皓骏的度量、标记、颜色、动画等功能，不仅可以凸显题目的条件与结论，还可动态呈现且有广度地表征数量关系，拓宽学生的解题思路，培养学生思维的发散性.

例如图1，在△ABC中，AB=AC，D为BC边上中点，点D到AB，AC的距离分别为DE，DF，则DE，DF有什么关系？

图1

此题涉及等腰三角形的性质、全等三角形的判定与性质、角平分线的性质等相关知识，条件简单明了，难度不大，学生易证结论.但在常态课中，教师首先引导学生审题，再尺规作图，通过度量出线段长度进行猜想并证明结论.一方面，部分教师对于此类题目仅局限于学生会求解即可，忽视引导学生有广度地深入探究问题的本质；另一方面，虽然部分教师意识到一题多解的重要性，但是传统课堂的局限性使得探究结果仅浮于表面，学生只是从“学不会”转向“学会”，并未从“不会学”转向“会学”.运用Hawgent皓骏，教师只需要通过拖动功能，即可使等腰三角形具有一般性；通过颜色标识和闪动功能，多种表征方式刺激学生的视觉系统，激发学生发散思维，启发学生从多角度寻求解决问题的方法.首先，拖动点A，可任意改变等腰三角形的大小与形状，使△ABC具有一般性，闪动△BDE和△CDF，启发学生从全等的角度证明线段相等（如图2）；接着，连接AD，标记并度量∠BAD和∠CAD，闪烁角平分线与角，凸显线段与角的位置与数量关系；然后，再次拖动点A，改变角的大小，引导学生利用角平分线的性质证明结论（如图3）；最后，用颜色分类标识各边，分别闪动线段与填充面，视觉上刺激学生思维，引导并启发学生从面积法的角度再次去证明线段全等（如图4）.

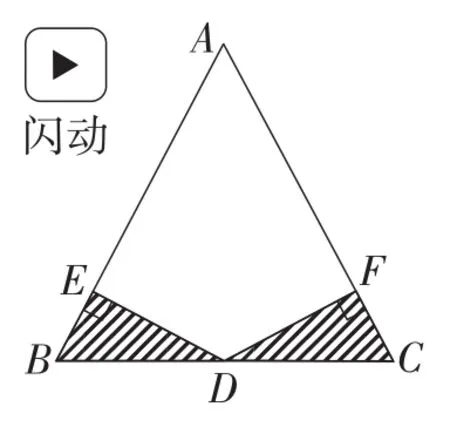
图2

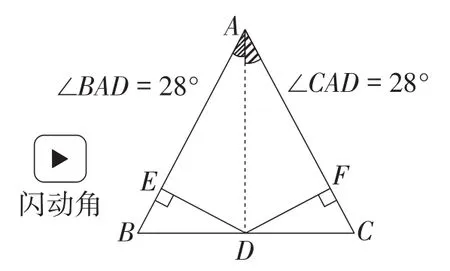
图3

图4

二、“数”“形”相依，理解知识的生成性

如果说一题多解是从材料的内在培养学生的发散性思维，那么一题多变即是从材料的外在发展学生的创造性思维.一题多变即是在不改变题目实质的情况下，对条件、结论等进行改造，从不同方位揭示题目的本质属性.一题多变强调题目的层次性，变式后的题目与原题目的联系性、启发性会直接影响学生知识结构的系统化.对于改变条件，结论截然相反的变式题目，传统的尺规作图过于刻板与僵化，无法生动、形象地实现原题到变式题“变”的过程，更无法直观化结论的多重性.Hawgent皓骏可以动态呈现“变”的过程，有效突破知识难点，动态化、直观化与明朗化隐匿的数量关系，帮助学生理解知识的形成、发生和发展过程，提高学生的分析问题和解决问题的能力.

变式1：如图5，在△ABC中，AB≠AC，D为BC边上的中点，点D到AB，AC的距离分别为DE，DF，则DE，DF又有什么关系？

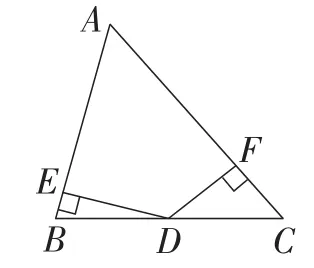
图5

此题是对例题的条件进行变式，即改变△ABC的形状，涉及到三角形底边中点的性质和三角形面积等相关知识，题目条件较少，结论较隐晦.教师仅依托传统的尺规作图、板书讲解题目，难以凸显条件与结论的内在联系，不利于启发学生在短时间内寻求解决问题的正确方法.欲轻松破解此难点，Hawgent皓骏或许是有效的选择.首先，度量各边数据，通过拖动点A，数形结合直观化AB，AC，DE，DF各边的关系与结论的双重性（如图6），引导学生运用分类讨论的思想，猜想结论：当AB＞AC时，DE＜DF；当AB＜AC时，DE＞DF.接着，作出垂线AG，同时闪动AG，BD，CD，可发现△ABD和△ACD是等底同高三角形（如图7）；然后，用颜色分类标识各边，进一步闪动线段与填充面，从数据、颜色、动画等多角度刺激学生的思维（如图8）；最后，小组合作，引导学生用面积法理论证明归纳猜想得到的结论，使得学生对题目的本质理解从感性层面上升到理性层面.

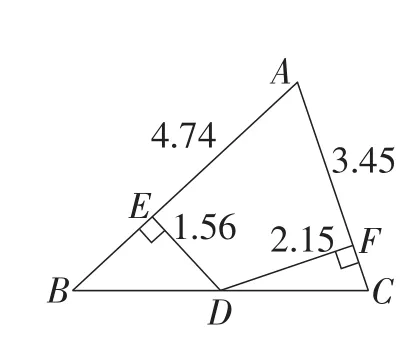
图6

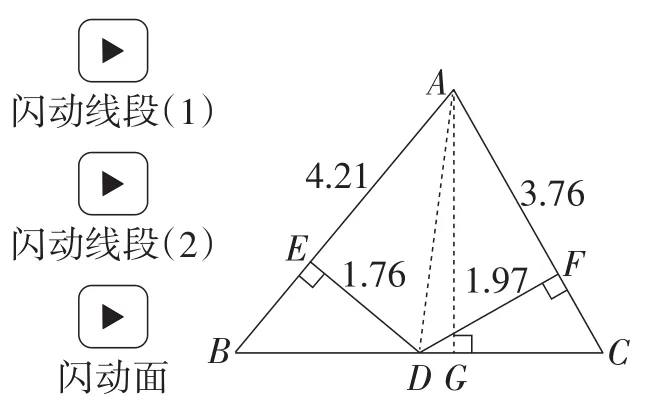
图7

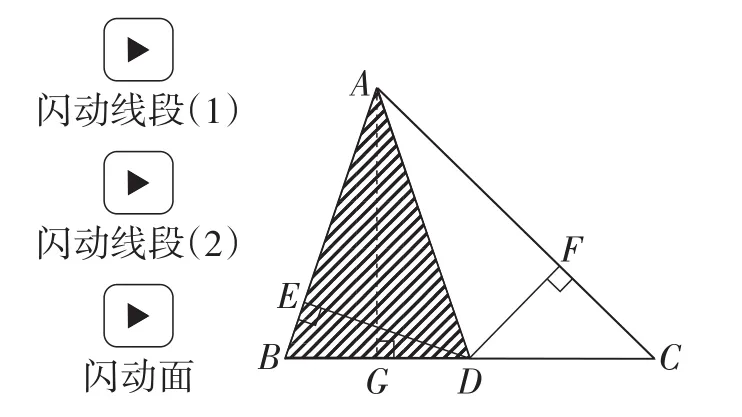
图8

三、“动”“静”合一，把握结论的不变性

一般而言，几何类变式主线为：形状→大小→位置.与形状变相比，位置变则是更深层次的构造.位置变可以使静态的问题转化为动态的问题，而动态题型较为抽象，知识综合性强，且是中考的热点、难点.传统课堂一般采用“想象”的方式模拟动点的运动过程或用尺规作图静态呈现图形，学生理解起来较为吃力.Hawgent皓骏的合理使用则可有效弥补传统课堂的短板，视觉化运动过程，把握动点变中不变的特征，不仅提高了课堂效率，而且极大地促进了学生思维的深刻性.

变式2：如图9，在△ABC中，AB=AC，D为BC边上一点（或BC边延长线上一点），点D到AB，AC的距离分别为DE，DF，点C到AB的距离为CG，则DE，DF，CG有什么关系？

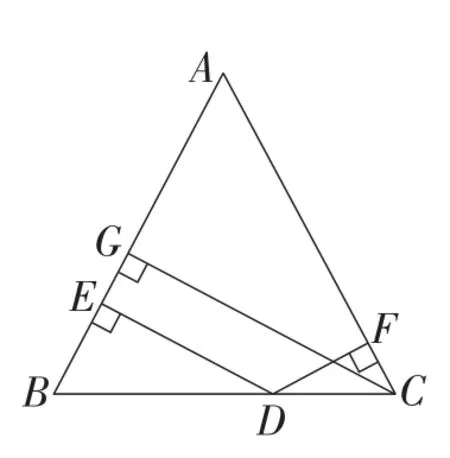
图9

此题是对例题的条件与结论同时进行变式，也是对点D的位置进行改变，涉及平行四边形的性质、全等三角形的判定、等量代换等知识点，综合性强、难度较大.由于传统教学单一的表现形式，以及手动作图的烦琐与低效等局限性，部分教师选择采用“填鸭式”教学模式处理动点问题，学生被动接受知识，不利于对学生数学抽象与空间想象能力的培养.而Hawgent皓骏的融入，为突破难点提供了可能，能够为学生增效减负.以点D在BC边上为例，首先，拖动点D，可发现，当点D为极端值时，DE+DF=CG（如图10）；接着，运用Hawgent皓骏的度量与计算功能，再次拖动点D，进一步发现，无论点D处于BC边上任何位置，仍可得到结论DE+DF=CG（如图11）；然后，引导学生小组合作交流，进一步证明结论；最后，类比点D在BC边上，对点D在BC边延长线上的猜想与证明，得到结论DE-DF=CG（如图12）.

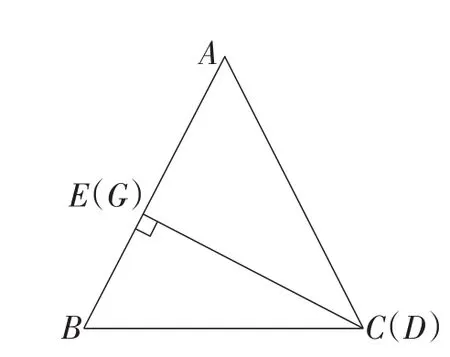
图10

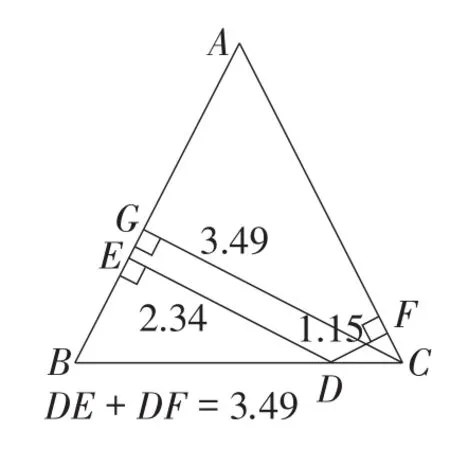
图11

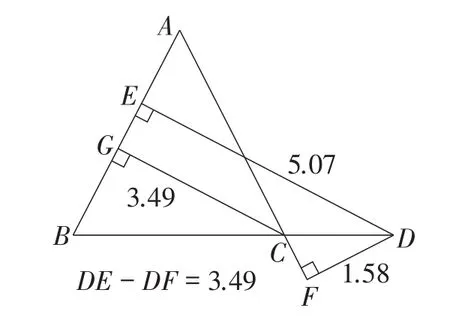
图12

《义务教育数学课程标准（2011年版）》（以下简称《标准》）强调，要以学生为主体，着眼于学生整体素质的提高，提升学生的数学素养.《标准》实施后，新的教学模式层出不穷，尤其是变式教学受到了大部分教育工作者的推崇.数学变式教学模式，有效培养了学生思维的广阔性、深刻性、全面性和创造性，提高了课堂教学效率.但是在变式过程中，数或形的细微变化却有可能带来截然相反的结论，传统教学对于处理“牵一发而动全身”的知识常常费时耗力，教学效果也不明显.动态数学技术的可视化、直观化等特点恰好弥补了课堂实施变式教学的局限性，提高了变式教学的效率.此外，变式教学也为信息技术的融合提供了理论指导.动态数学技术与变式教学的有机结合，使得晦涩难懂的知识变得简单有趣，极大地促进了学生学习数学的兴趣，提高了学生学习数学的信心，发展了学生的几何直观和推理能力.