FTS干涉信号延时补偿算法的仿真分析

翟茂林 李涛 张玉贵



FTS干涉信号延时补偿算法的仿真分析

翟茂林1,2李涛1张玉贵1

（1 北京空间机电研究所，北京 100094） （2 北京市航空智能遥感装备工程技术研究中心，北京 100094）

基于干涉分光原理的傅里叶变换光谱仪通过将激光信号作为采样参考信号对干涉信号进行等光程差采样，然而动镜扫描不稳以及后续焦平面电路的差异会造成干涉信号与激光参考信号之间存在相对延时，导致数据的非同步性。随着多元探测器技术的快速发展，探测器信号路数急速扩展，目前广泛采用添加延时线的延时补偿方法需要大量硬件配置将不再适用。文章针对该问题提出一种延时补偿的软件实现方法，利用通过建模仿真得到的干涉数据完善了激光信号过零点获取、干涉数据重构等算法，并通过MATLAB进行了补偿原理的仿真分析。结果表明：通过该算法对干涉信号进行延时匹配重采样，可以将相对延时补偿到1μs以内，光谱复原度高于99%，可较好抑制动镜扫描不稳带来的光程差采样误差。用于高光谱遥感的后期数据处理，可有效提高光谱复原精度。

傅里叶变换光谱仪 延时补偿 干涉图重构 高光谱遥感

0 引言

傅里叶变换光谱（Fourier Transform Spectra，FTS）技术与传统光栅或滤光片分光的光谱仪的区别是利用了干涉信号和光谱信号之间傅里叶变换与反变换的对应关系[1-3]，通过测量目标的干涉信号并对其进行傅里叶变换来测定和研究目标光谱特征。FTS技术以其光通量大、光谱通道数多[4]、光谱分辨率高[5]等诸多优点，已经成为光学研究特别是环境气体监测领域研究的热点。

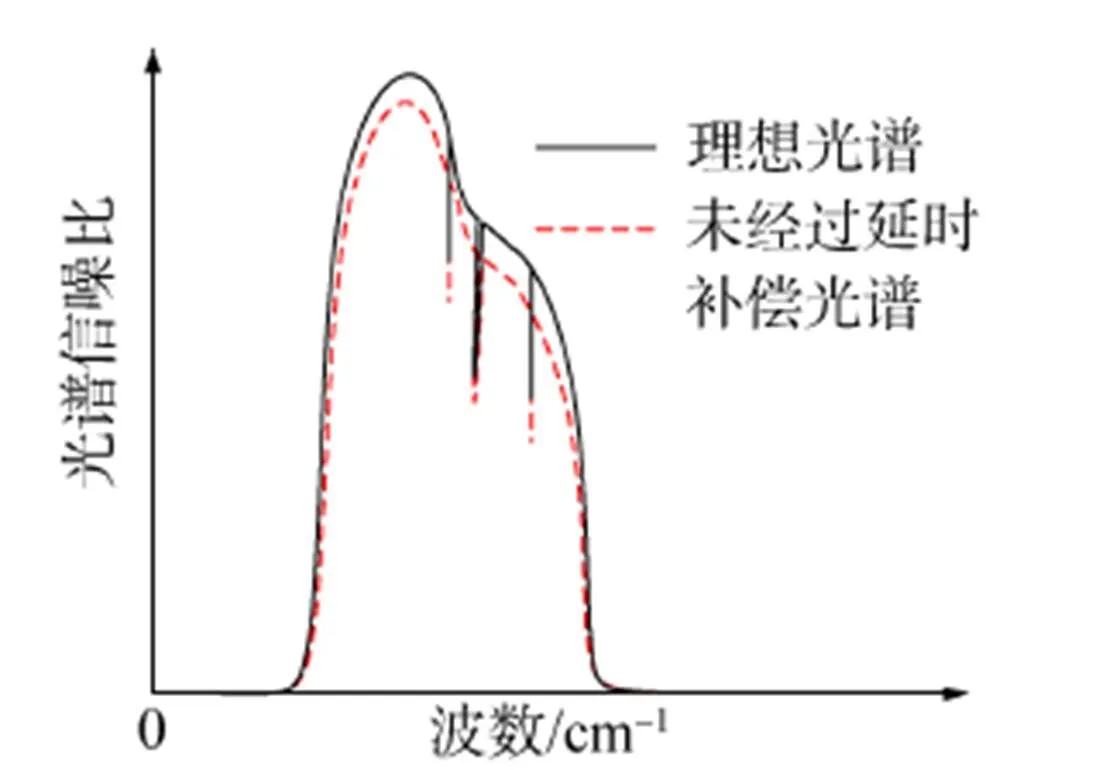
图1 二路信号相对延时对光谱信噪比的影响

在基于FTS技术的光谱探测领域中，要求干涉信号与激光参考信号（简称激光信号，仅1路）之间具有很好的同步性，以此来大大降低动镜扫描速度不稳引入的光程差采样误差[6-8]，从而提高仪器的信噪比。“风云三号”卫星高光谱温室气体监测仪和“高分五号”卫星大气环境甚高光谱分辨率探测仪在地面测试过程中的数据结果均表明，当动镜扫描速度稳定性不够且干涉信号与激光信号相对延时差别较大时，系统的光谱信噪比也将明显下降[9]，复原光谱出现明显失真问题，如图1所示。

目前，常用傅里叶变换光谱仪的探测器通常是单元型的，因此只生成几路干涉信号。例如：“高分五号”卫星大气环境甚高光谱分辨率探测仪输出二路干涉信号；“风云三号”卫星高光谱温室气体监测仪输出的干涉信号为四路[10]。鉴于单元型探测器生成的信号路数有限，一般通过在激光信号或干涉信号的硬件链路上添加延时线，将二者之间的相对延时补偿到1μs以内，使之几乎同时到达AD转换器，消除采样误差。由于信号路数少，硬件延时匹配方法的调试工作量可以接受。

单元型探测光谱仪的探测模式是打点法，每个扫描周期只能实现地面一个点的光谱探测，采用多个单元型探测器通常是为了实现更宽的谱段覆盖而非探测范围。另外，为了实现更高的光谱分辨率，通常每个扫描周期需要几秒到十几秒[11-12]，因此采用单元型探测器的光谱仪的探测效率很低。为提高星载光谱仪的探测效率，基于FTS技术的光谱仪的探测器逐渐向多元、线元、小面元探测器的方向发展。随着多元探测器技术的快速发展，探测器输出的信号路数急速扩展[13-15]，添加延时线的方法需要大量硬件配置将不再适用。

为解决多元探测器的信号同步探测问题，本文从基于FTS技术的光谱仪的实际应用出发，提出干涉信号延时匹配的软件实现算法，通过该算法来补偿干涉信号与激光信号之间的相对延时，解决二路信号的同步探测问题，抑制动镜扫描速度不稳带来的光程差采样误差，提高系统光谱复原精度。

1 延时补偿

利用软件方法实现干涉信号与激光信号之间的延时补偿，即针对存在相对延时的两原始信号，寻找信号的特征位置作为标定位置，得到相对延时时间，进而在干涉信号的原采样位置补偿该相对延时，在新的经过延时补偿后的采样位置对干涉信号进行重新采样，最后对重采样的干涉数据反演得到新的光谱图，与原干涉信号反演得到的光谱图进行比较分析。

首先根据信号之间相对延时的产生原因，为干涉信号的延时匹配算法制定总体实现方案，将实现目标分步处理，概括为几个步骤，如图2所示。

图2 延时补偿算法流程

1.1 数据的建模与仿真

根据傅里叶变换光谱仪的结构及工作特点，建立干涉信号与激光信号模型，并进行加噪处理与仿真，为算法研究及其效果比对提供输入数据。傅里叶变换光谱仪以迈克尔逊干涉仪为原型[16-18]，其结构及工作原理如图3所示。

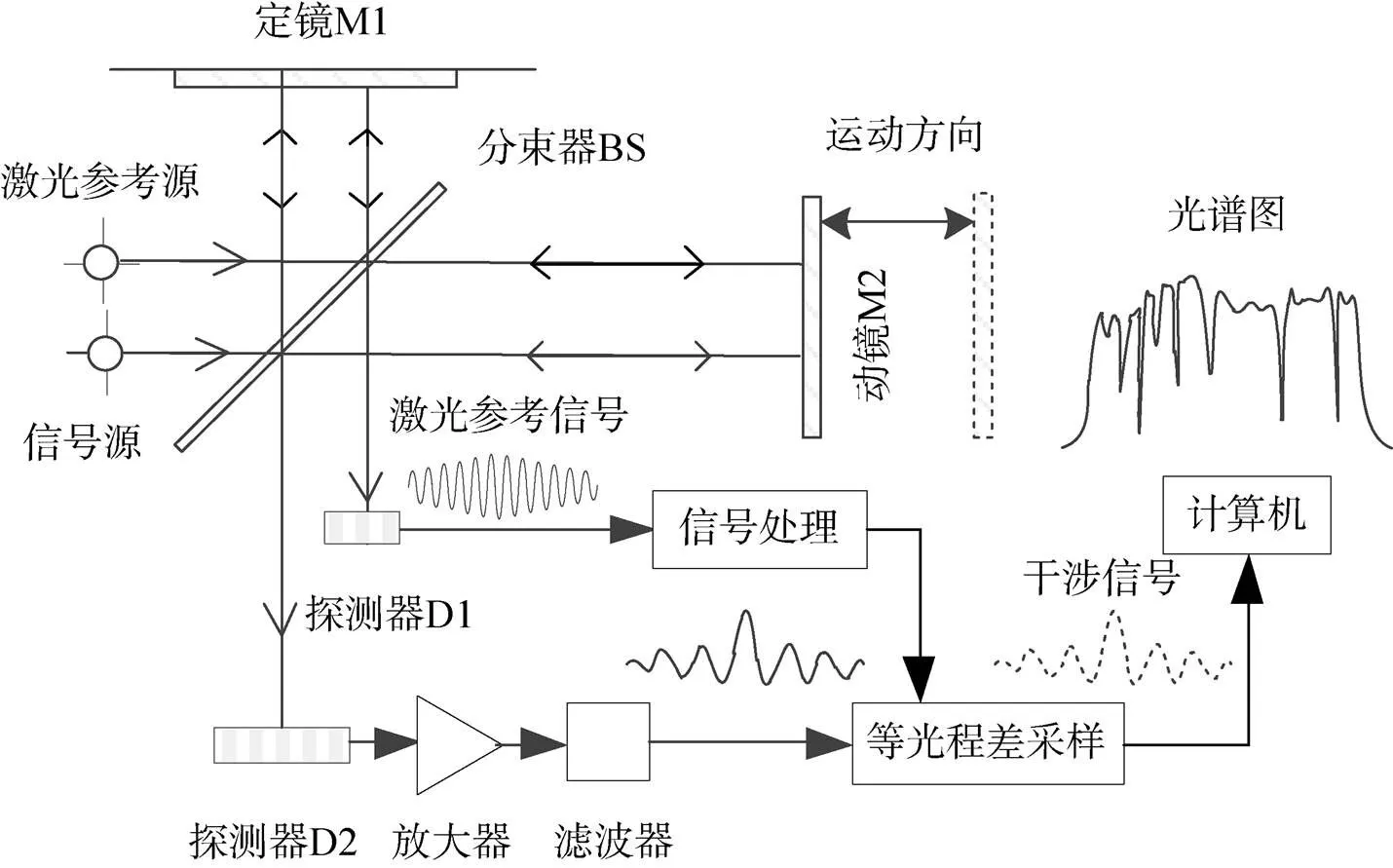
图3 傅里叶变换光谱仪工作原理

如图3所示，前端干涉仪系统通过分束器将入射光等分为两束，同源的两束相干光分别经定镜与动镜反射后在探测器端形成干涉。随着动镜的扫描运动改变光程差，最终在探测器上形成干涉信号。实际光谱仪中通过设置一台与大气干涉仪共光路的激光干涉仪系统，以激光干涉信号的过零点位置作为等光程差采样模拟干涉信号的触发信号，完成干涉信号的采集。

根据文献[17]，光谱仪中光程差op的函数表达式为

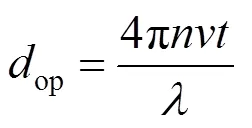
式中为介质折射率；为动镜的扫描速度；为时间；为入射光波长。

对于理想单色光，其干涉光光强为单频正弦波信号

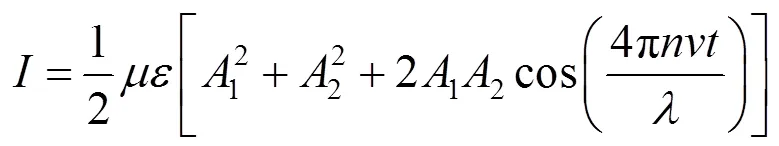
式中1，2为光波振幅；为介电常数；为磁导率。

对于复色光，其光强oσ是入射光波数的函数，则波数为的光波干涉之后在探测器上的光强I为

式中为分束器反透比。

复色光的入射光线具有一定谱段范围，因此探测器接收到的光强（Σ()）是各个波长的光的干涉信号I的积分

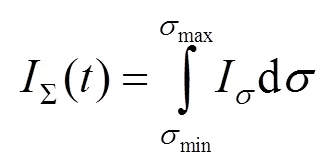
式中max，min为光谱范围内对应的最大波数和最小波数。

为简化计算，这里设定入射光光强oσ的幅度为恒定值，即一段矩形谱密度光谱，同时设定动镜扫描速度波动模型为

式中jitter为动镜扫描时波动的速度；0为理想恒定扫描速度；为速度波动幅值；f为速度波动的变化频率。

该速度波动下的光程差op表达式为

则动镜扫描速度波动下的复色光干涉信号表达式为

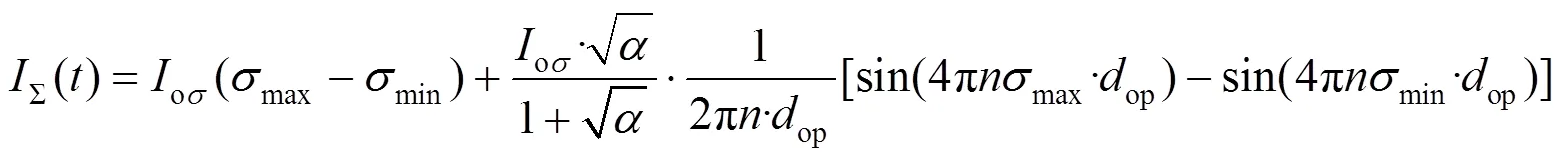
根据上述对干涉信号的推导和分析，用MATLAB进行仿真得到干涉数据，仿真条件如表1所示，信号仿真波形如图4所示，干涉信号为类sinc信号，激光信号为正弦波。

表1 仿真参数设置

Tab.1 Parameter setting of simulation

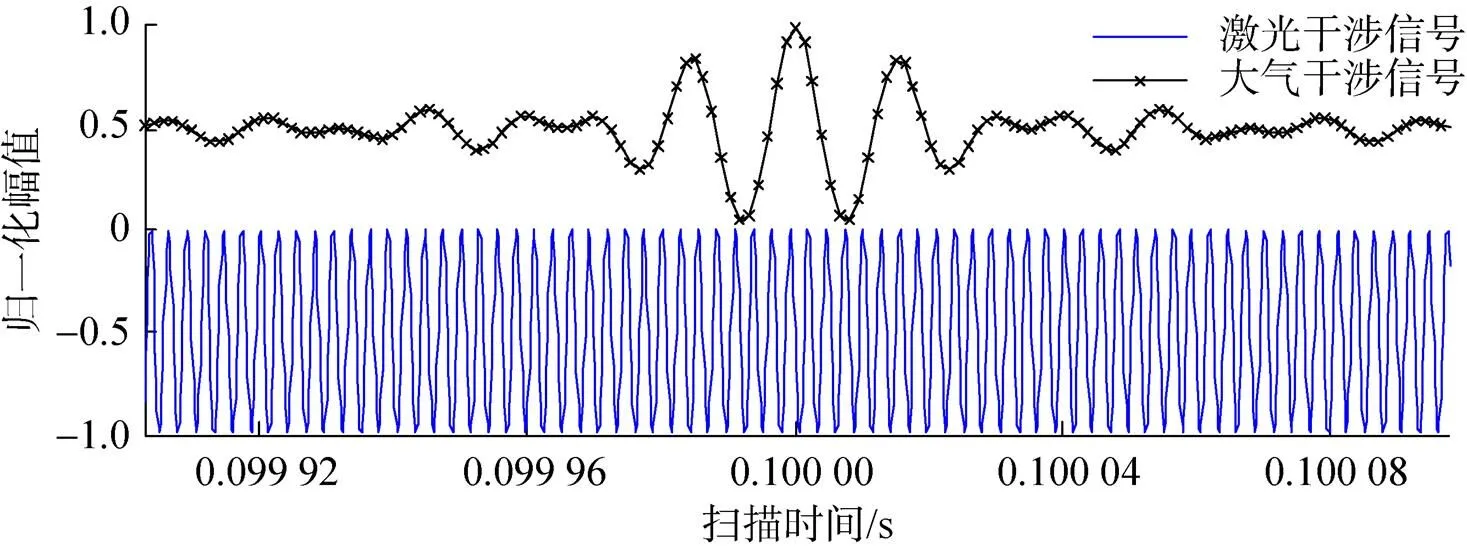
图4 同步的干涉信号与激光信号仿真波形

本文用上述仿真数据模拟实际数据采集系统中利用同步时钟高频采样得到的原始干涉信号与激光信号，作为后续算法实现与结果验证的数据源。

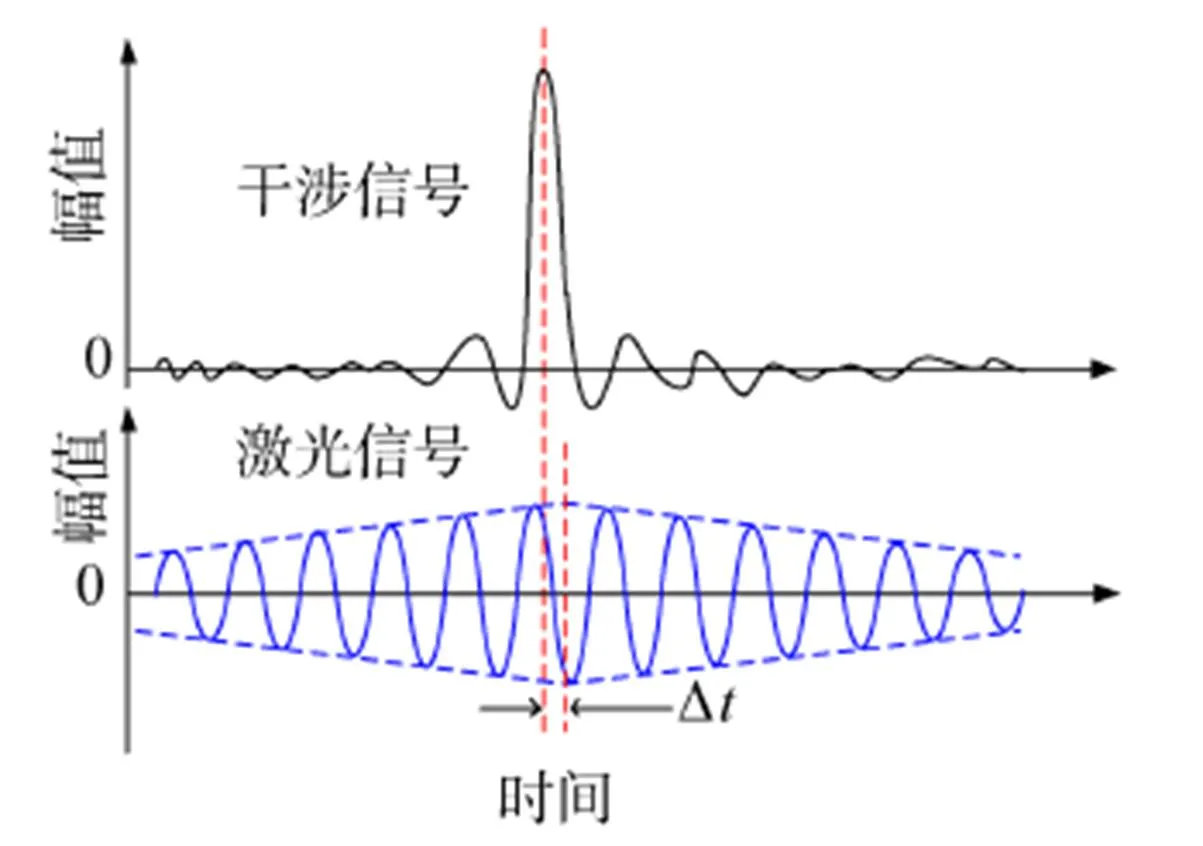
图5 干涉信号与激光信号的波形特征

1.2 延时标定算法

干涉信号与激光信号的相对延时是进行延时补偿的重要依据，其准确性决定了延时匹配的精度。标定依据是根据干涉信号和激光信号的波形特点，寻找其特征位置，进而标定出二者的相对延时。如图5所示，干涉信号的特征非常明显，其中间幅度大、两翼幅度小，是典型的类sinc函数；同样，受干涉仪结构及工作特点的影响，激光信号会出现“纺锤”形包络，波形呈现出“纺锤”效应。

为精确标定二路信号之间的相对延时，提出两种延时标定方法：

1）将二路信号的最大值点作为特征位置来标定延时；

2）利用“波形重心法”进行延时标定。

对于干涉信号来说，“波形重心法”计算公式为

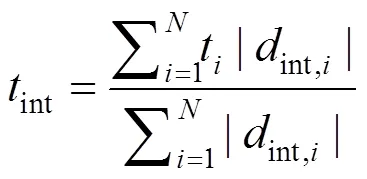
式中int为干涉信号重心位置；为高频采样数据标号，1~；t为高频采样时间点；int,i为干涉信号幅值。

同理，激光信号的重心位置为

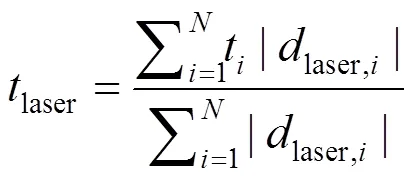
式中laser为激光信号的重心位置；laser,i为激光信号幅值。

那么，其相对延时为

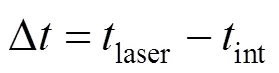
1.3 激光过零点获取算法

由于动镜的扫描速度不稳定，激光信号的各个过零点之间在时间轴上未必是等间隔的，但从光程差的角度却是等间隔的，即激光信号的过零点是对干涉信号进行等光程差采样的理想位置。激光的干涉信号为正弦波，为准确获取其过零点，本文采用了分段正弦波插值[19-21]对激光信号进行拟合，进而解算出激光信号各个过零点时刻，即干涉信号的等光程差采样时间点zcp,j。仿真结果如图6所示。

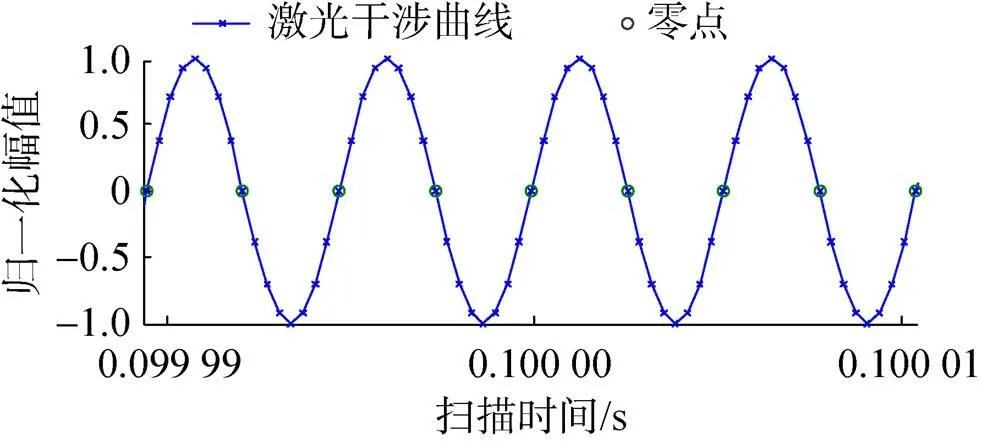
图6 激光信号过零点获取

1.4 干涉信号采样位置延时补偿

傅里叶变换光谱仪以激光信号过零点作为触发，实现对干涉信号进行等光程差采样的目的，由于实际干涉信号与激光信号之间存在相对延时，使得在激光信号过零点时刻不能立即对干涉信号进行采样。为保持二者的同步，利用前一步标定的相对延时Δ，对原等光程差采样时间点zcp,j进行延时补偿，得到干涉信号的零延时等光程差采样时间点

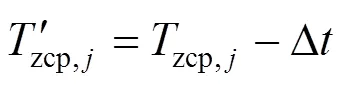
完整的延时补偿原理示意如图7所示。横坐标表示时间，Δ可以认为是一个时间当量。

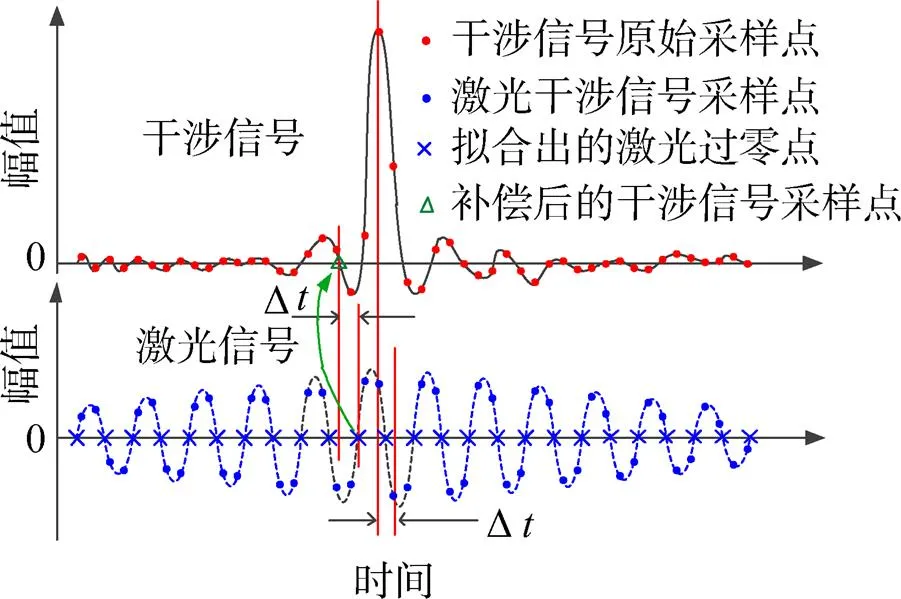
图7 完整延时匹配流程示意

1.5 干涉数据重构与光谱复原验证

由于光谱仪系统最终需要保证光谱维的保真度，因此通过将重构的干涉信号复原到光谱来验证延时匹配算法的效果和精度。首先将存在相对延时的原干涉信号（简称原干涉信号）进行FFT变换，得到原始的存在相对延时的光谱图，而后将经过延时匹配算法处理的干涉信号（简称匹配干涉信号）做同样处理，最后将两光谱图分别与理想光谱进行比对和分析。本文利用复原后的光谱与理想光谱之间的误差率（两光谱各对应点幅值误差的加和与理想光谱幅值加和的比值）来评价延时匹配算法效果。

原干涉信号生成的带有相对延时的光谱图相对理想光谱的误差率为

式中del为原始光谱相对理想光谱的误差率；为光谱数据标号，1~；ideal,k为理想光谱图的光谱数据幅值；del,k为原始附带延时光谱图的光谱数据幅值。

同理，经过延时匹配后的光谱图相对理想光谱的误差率为

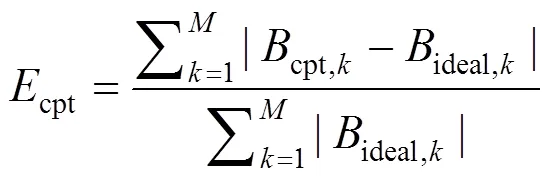
式中cpt为延时匹配后的光谱相对理想光谱的误差率；cpt,k为延时匹配后的光谱图的光谱数据幅值。

2 延时补偿仿真分析

根据前面对干涉信号模型的推导与仿真，以及延时匹配各个环节的分析，依照表1参数设定，利用MATLAB工具进行仿真。由式（7）可看出干涉信号中包含相当比重的直流分量，且该部分不会对傅里叶变换后得到的光谱图形状产生影响，因此这里进行了滤波处理。干涉信号仿真结果如图8所示。

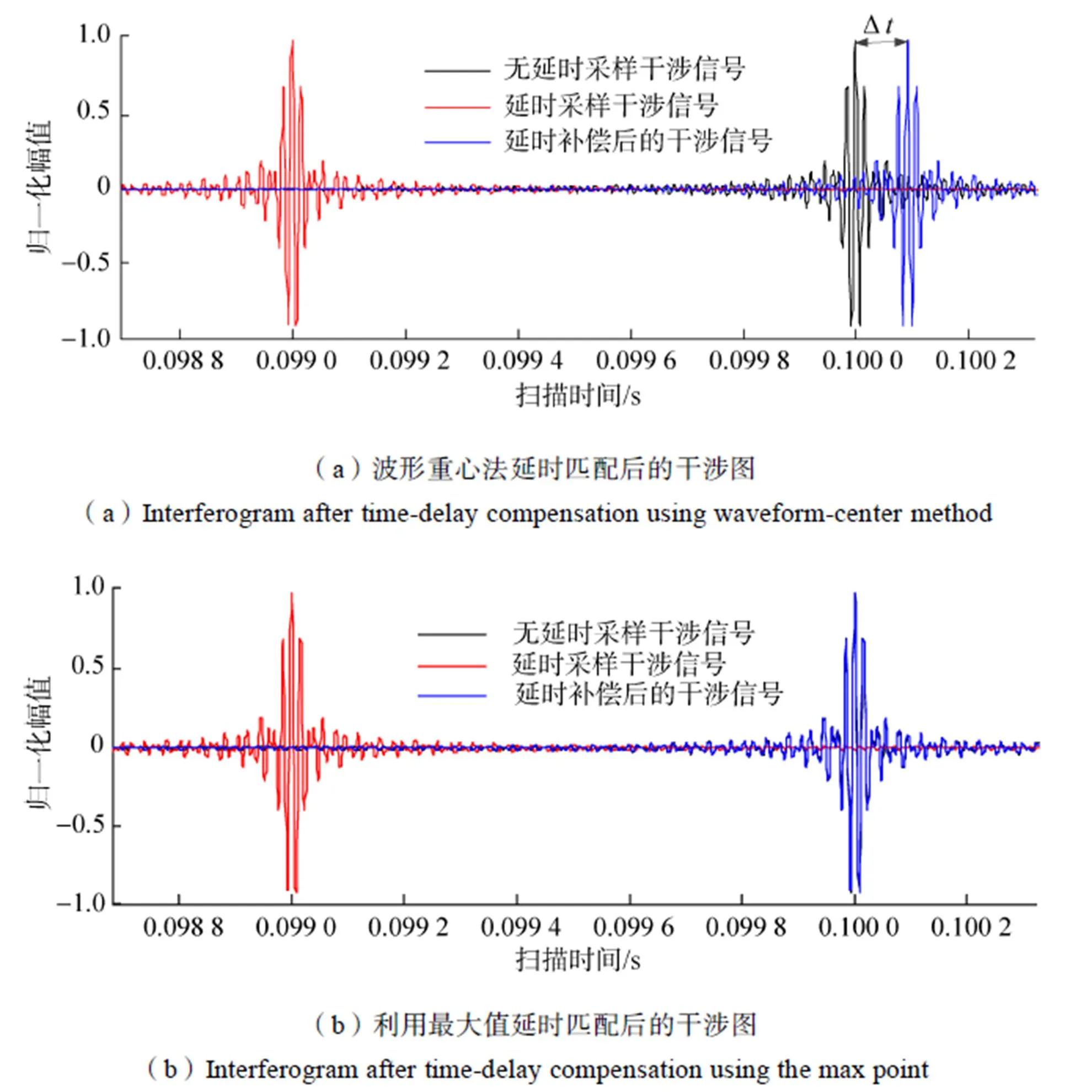
图8 干涉信号延时匹配算法仿真

图8（a）仿真结果显示，采用“波形重心法”进行延时标定，干涉信号与激光信号之间依然存在一定延时∆。经过仿真和分析得出，“波形重心法”延时匹配效果不理想是由于动镜扫描速度不稳定，干涉信号并非严格关于零光程差位置对称的类sinc信号。这种不严格对称使得波形重心相对其理想位置出现偏差，导致利用“波形重心法”进行延时定标得到的结果不准确。

图8（b）是利用波形最大值点作为特征位置，进行延时标定后的干涉图。仿真数据显示相对延迟时间Δ从1ms校正到了0.016μs，远低于1μs的基本要求，明显好于第一种方法。该延时补偿精度满足对光谱复原精度的要求，可以达到替代硬件延时匹配的目标要求。另外可以通过采集更多的干涉信号数据点继续提高延时补偿的精度，但考虑到算法运行带来的时间成本，更高的匹配精度没有太大的必要性。

对上述干涉信号进行光谱复原，通过与理想光谱进行比对来验证延时匹配算法的效果和精度，光谱图仿真结果如图9所示。

图9 干涉信号光谱复原仿真

从图9可看出，存在相对延时的光谱相比理想光谱出现了明显的光谱失真问题，尤其在光谱边缘位置出现严重的频谱泄露。而经过延时补偿算法处理过的光谱可以明显改善光谱复原精度。具体计算结果如表2所示。

表2 仿真结果

Tab.2 Simulation results

根据表2仿真数据，相对延时从1ms补偿到了1μs以内，补偿效果可以达到硬件延时匹配的水平；经过延时补偿后光谱的误差率从原光谱图的6%降低到1%以下，延时匹配后的光谱复原精度高于99%，光谱保真度明显提高。

3 结束语

本文基于多元探测器快速发展的背景下多信号链路无法实现同步采样的问题，提出一种基于软件实现干涉信号延时补偿的算法，通过推导基于傅里叶变换光谱技术的干涉信号，建立了动镜扫描不稳情况下干涉信号的数学模型，制定了延时匹配总体实现方案并完成各步的算法设计，最终仿真结果表明，该算法对干涉信号非同步采样导致的光谱复原精度下降问题具有较好的修正效果，这为后续采用FPGA+DSP的硬件架构进行硬件实现提供了理论支撑。

[1] THURMAN S T, FIENUP J R. Fizeau Fourier Transform Imaging Spectroscopy: Missing Data Reconstruction[J]. Optics Express, 2008, 16(9): 6631-6645.

[2] SELLAR R G, RAFERT J B. Fourier Transform Imaging Spectrometer with a Single Toroidal Optic[J]. Applied Optics, 1995, 34(16): 29-31.

[3] KAWATA S, MINAMI K, MINAMI S. Super Resolution of Fourier Transform Spectroscopy Data by the Maximum Entropy Method[J]. Applied Optics, 1983, 22(22): 3593-3598.

[4] 夏翔, 华建文, 段娟, 等. 傅里叶变换光谱仪动镜速度波动分析研究[J]. 科学技术与工程, 2014, 14(20): 72-76. XIA Xiang, HUA Jianwen, DUAN Juan, et al. Analysis of Speed Fluctuation of Moving Mirror in Fourier Transform Spectrometer[J]. Science Technology and Engineering, 2014, 14(20): 72-76. (in Chinese)

[5] TENG Y C, ROYCE B S. Quantitative Fourier Transform IR Photoacoustic Spectroscopy of Condensed Phases[J]. Applied Optics, 1982, 21(1):77-80.

[6] 相里斌. 傅里叶变换光谱仪中的主要技术环节[J]. 光子学报, 1997(6): 550-554.XIANG Libin. The Key Design Issues in Fourier Transform Spectrometers[J]. Acta Photonica Sinica, 1997(6): 550-554. (in Chinese)

[7] 龚忠清, 孙晓兵, 张荞, 等. 傅里叶变换红外光谱仪偏振标定[J]. 量子电子学报, 2011, 28(2): 142-146. GONG Zhongqing, SUN Xiaobing, ZHANG Qiao, et al. Calibration of Polarimetric Fourier Transform Infrared Spectrometer[J]. Chinese Journal of Quantum Electronics, 2011, 28(2): 142-146. (in Chinese)

[8] WEN W, ZHANG H Y, XIE F L. Design and Implementation of Data Acquisition Network Based on RFID[J]. Electronic Design Engineering, 2009(10): 157-162.

[9] LUC P, GERSTENKORN S. Fourier Transform Spectroscopy in the Visible and Ultraviolet Range[J]. Applied Optics, 1978, 17(9): 1327-1331.

[10] 张淳民, 穆廷魁, 颜廷昱, 等. 高光谱遥感技术发展与展望[J]. 航天返回与遥感, 2018, 39 (3): 108-118. ZHANG Chunmin, MU Tingkui, YAN Tingyu, et al. Overview of Hyperspectral Remote Sensing Technology[J]. Spacecraft Recovery & Remote Sensing, 2018, 39 (3): 108-118. (in Chinese)

[11] 董欣, 徐彭梅, 侯立周. 大气环境红外甚高光谱分辨率探测仪设计与实现[J]. 航天返回与遥感, 2018, 39(3): 38-47. DONG Xin, XU Pengmei, HOU Lizhou. Design and Implementation of Atmospheric Infrared Ultra-spectral Sounder[J]. Spacecraft Recovery & Remote Sensing, 2018, 39(3): 38-47. (in Chinese)

[12] 熊伟. 星载超光谱大气主要温室气体监测仪载荷[J]. 航天返回与遥感, 2018, 39(3): 56-66. XIONG Wei. Hyperspectral Greenhouse Gases Monitor Instrument (GMI) for Spaceborne Payload[J]. Spacecraft Recovery & Remote Sensing, 2018, 39(3): 56-66. (in Chinese)

[13] TENG Y C, ROYCE B S. Quantitative Fourier Transform IR Photoacoustic Spectroscopy of Condensed Phases[J]. Applied Optics, 1982, 21(1): 77-80.

[14] 范松灿. 傅立叶变换红外光谱仪的原理与特点[J]. 科技创新与生产力, 2007(11): 40-41.FAN Songcan. The Principle and Characteristic of the FTIR Spectrometer[J]. Technology Innovation and Productivity, 2007(11): 40-41.(in Chinese)

[15] 吴瑾光. 近代傅里叶变换红外光谱技术及应用[M]. 北京: 科学技术文献出版社, 1994. WU Jinguang. Modern Fourier Transform Infrared Spectroscopy and Its Application[M]. Beijing: Science and Technology Academic Press, 1994. (in Chinese)

[16] 翁诗甫. 傅里叶变换红外光谱仪[M]. 北京: 化学工业出版社, 2005. WENG Shifu. Fourier Transform Infrared Spectrometer[M]. Beijing: ChemicalIndustryPress. 2005. (in Chinese)

[17] 王建波, 姜旭峰. 浅谈傅立叶变换红外光谱仪的原理及使用[J]. 科技风, 2011(18): 124.WANG Jianbo, JIANG Xufeng. Principle and Application of Fourier Transform Infrared Spectrometer[J]. Technology Trend, 2011(18): 124. (in Chinese)

[18] 吕群波, 姚涛, 相里斌, 等. 干涉数据光谱反演方法研究[J]. 光谱学与光谱分析, 2010, 30(1): 114-117.LYU Qunbo, YAO Tao, XIANG Libin, et al. Spectrum Recovery Method for Interferometric Data[J]. Spectroscopy and Spectral Analysis, 2010, 30(1): 114-117. (in Chinese)

[19] 江舸, 陶荣辉, 李钒, 等. 基于FPGA实现的FFT插值正弦波频率估计[J]. 太赫兹科学与电子信息学报, 2009, 7(6): 569-572.JIANG Ge, TAO Ronghui, LI Fan, et al. FFT Interpolation Sinusoidal Frequency Estimation Based on FPGA[J]. Journal of Terahertz Science and Electronic Information Technology, 2009, 7(6): 569-572. (in Chinese)

[20] 李耀彬, 曾祥斌, 沈铖武. 基于抛物线插值的正弦波拟合算法[J]. 计算机工程与设计, 2009, 30(11): 2793-2795.LI Yaobin, ZENG Xiangbin, SHEN Chengwu. Based on the Parabola Interpolation of Sine Fitting Method[J]. Computer Engineering and Design, 2009, 30 (11): 2793-2795. (in Chinese)

[21] 张松. 基于FFT的正弦信号频率估算新方法[J]. 大理大学学报, 2009, 8(8): 36-39.ZHANG Song. A New FFT Based on Algorithm for Sinusoid Frequency Estimation[J]. Journal of Dali University, 2009, 8(8): 36-39. (in Chinese)

[22] 朱超, 鲁昌华, 刘文清, 等. FTIR干涉图相位校正技术的研究[J]. 电子测量与仪器学报, 2013, 27(7): 663-668. ZHU Chao, LU Changhua, LIU Wenqing, et al. Study on Phase Correction Technique of FTIR Interferogram[J]. Journal of Electronic Measurement and Instrument, 2013, 27(7): 663-668. (in Chinese)

[23] 李苏宁, 朱日宏, 李建欣, 等. 傅里叶干涉成像光谱技术中的重构方法[J]. 应用光学, 2009, 30(2): 354-360. LI Suning, ZHU Rihong, LI Jianxin, et al. Reconstruction Method in Fourier Interference Imaging Spectroscopy[J]. Applied Optics, 2009, 30(2): 354-360. (in Chinese)

[24] 李苏宁, 朱日宏, 高志山, 等. 共轭傅里叶变换校正成像光谱重构[J]. 光学学报, 2011, 31(4): 152-158. LI Suning, ZHU Rihong, GAO Zhishan, et al. Spectral Reconstruction of Corrected Imaging Using Conjugate Fourier Transform[J]. Acta Optica Sinica, 2011, 31(4): 152-158. (in Chinese)

[25] 李妍, 李胜, 高闽光,等. 两种红外干涉图采集及光谱复原方法的对比研究[J]. 光学学报, 2015, 35(9): 358-364.LI Yan, LI Sheng, GAO Minguang, et al. A Comparative Study of Two Infrared Interferogram Acquisition and Spectral Restoration Methods[J]. Acta Optica Sinica, 2015, 35(9): 358-364. (in Chinese)

Time-delay Compensation Simulation and Analysis of Interference Signal Based on FTS Technology

ZHAI Maolin1,2LI Tao1ZHANG Yugui1

（1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China） （2 Beijing Engineering Technology Research Center of Aerial Intelligent Remote Sensing Equipments, Beijing 100094, China）

As to Fourier Transform Spectrometer based on the Michelson Interferometer, a laser interference signal is provided as the reference signal to sample the interference signals with identical optical path difference. Both the dynamic instability of the scanning mirror and the difference of focal plane circuits will result in the relative time delay between the laser interference signal and the interference signal, causing non-synchronicity between the two signals. Currently, with the sharply increasing of the number of pixels on the focal plane, the signal links are such a large number that adding delay line is no longer applicable as a result of too much workload for hardware configuration. In this paper, a kind of software method for compensating the relative time delay is proposed to substitute the hardware method of adding delay line, and the principle of compensation is simulated and analyzed with MATLAB. The result shows that the relative time delay can be compensated to 1μs and the spectral recovery accuracy is higher than 99% by matching the time delay and resampling the interference signal. The sampling error of optical path difference caused by the unstable scanning speed of the moving mirror can be effectively suppressed. This method can be used in data processing of hyperspectral remote sensing and effectively improves the precision of spectral restoration.

Fourier Transform Spectrometer; time-delay compensation; interferogram reconstruction; hyperspectral remote sensing

TP732.2

A

1009-8518(2019)03-0047-10

10.3969/j.issn.1009-8518.2019.03.007

翟茂林，男，1992年生，2016年获山东大学自动化专业学士学位，现在中国空间技术研究院光学工程专业攻读硕士学位。研究方向为光电信息处理技术。Email：85136538@qq.com。

2019-01-25

地球观测与导航专项；国家重点研发计划项目：大气辐射超光谱探测技术（2016YFB0500700）

（编辑：王丽霞）