减速伞收口状态气动特性仿真与试验研究
王奇 王立武 张章 吴卓 雷江利 孙希昀
减速伞收口状态气动特性仿真与试验研究
王奇1,2王立武1,2张章1,2吴卓1,2雷江利1,2孙希昀1,2
(1 北京空间机电研究所,北京 100094) (2 中国空间技术研究院航天器无损着陆技术核心专业实验室,北京 100094)
减速伞是回收着陆系统中重要的气动减速装置,其气动特性关系着整个减速着陆过程的成败。由于减速伞开伞动压高、载荷大的特点,结构设计及参数选择非常关键,并且,为减小开伞动载,一般采用底边收口的形式控制伞衣逐级充气展开。文章所述的减速伞具有两级收口装置,基于某伞型为带条伞的减速伞进行了收口状态的数值仿真分析和风洞试验研究。利用流固耦合方法获得了减速伞的收口展开过程中典型阶段的气动外形,采用计算流体力学(Computational Fluid Dynamics,CFD)方法对收口状态下的减速伞进行了气动特性计算分析。同时,为考察减速伞收口状态的稳态阻力特性及收口解除过程中的阻力特性变化,并验证收口解除装置的工作可靠性,在亚声速风洞中对减速伞进行了稳态及动态解除收口试验。通过减速伞风洞实验,对其阻力面积及动态特性参数进行了测量,实验结果表明仿真计算能够较为准确的预测减速伞收口状态的气动及动力学特性,且误差不大于5%,从而能够为减速伞的结构及强度设计提供重要依据。
数值模拟 风洞试验 减速伞收口 气动特性 航天返回
0 引言
减速伞是航天器回收着陆过程中的重要减速装置,减速伞通常需实现大幅减小回收物速度和拉出主伞的功能,其性能和可靠性对返回任务的成败有着至关重要的影响。而收口技术是在充气展开过程中使减速伞分阶段充气展开,从而避免动压及载荷过大造成结构损坏,图1所示为典型的具有二级收口功能的减速伞伞衣气动外形示意图。收口展开过程本身是一个空气与结构高度非线性耦合的过程。且由于织物材料刚度小,变形速度快而复杂,减速伞周围的流场存在大范围流动分离,都增加了研究降落伞流场和动力学特性的难度。而数值仿真技术虽然能够节省大量的风洞试验成本,但对于复杂流固耦合问题的处理仍不完善。因此,将数值计算分析与风洞试验结合的方法在研制成本和时间上能够达到最佳的平衡。本文首先利用流固耦合方法初步建立减速伞在流场作用下的二级收口气动外形,进而通过流体力学(Computational Fluid Dynamics,CFD)方法对减速伞收口状态时的稳态流场进行高精度计算分析,最终通过与风洞试验数据对比来验证数值模拟方法的可行性及准确性。
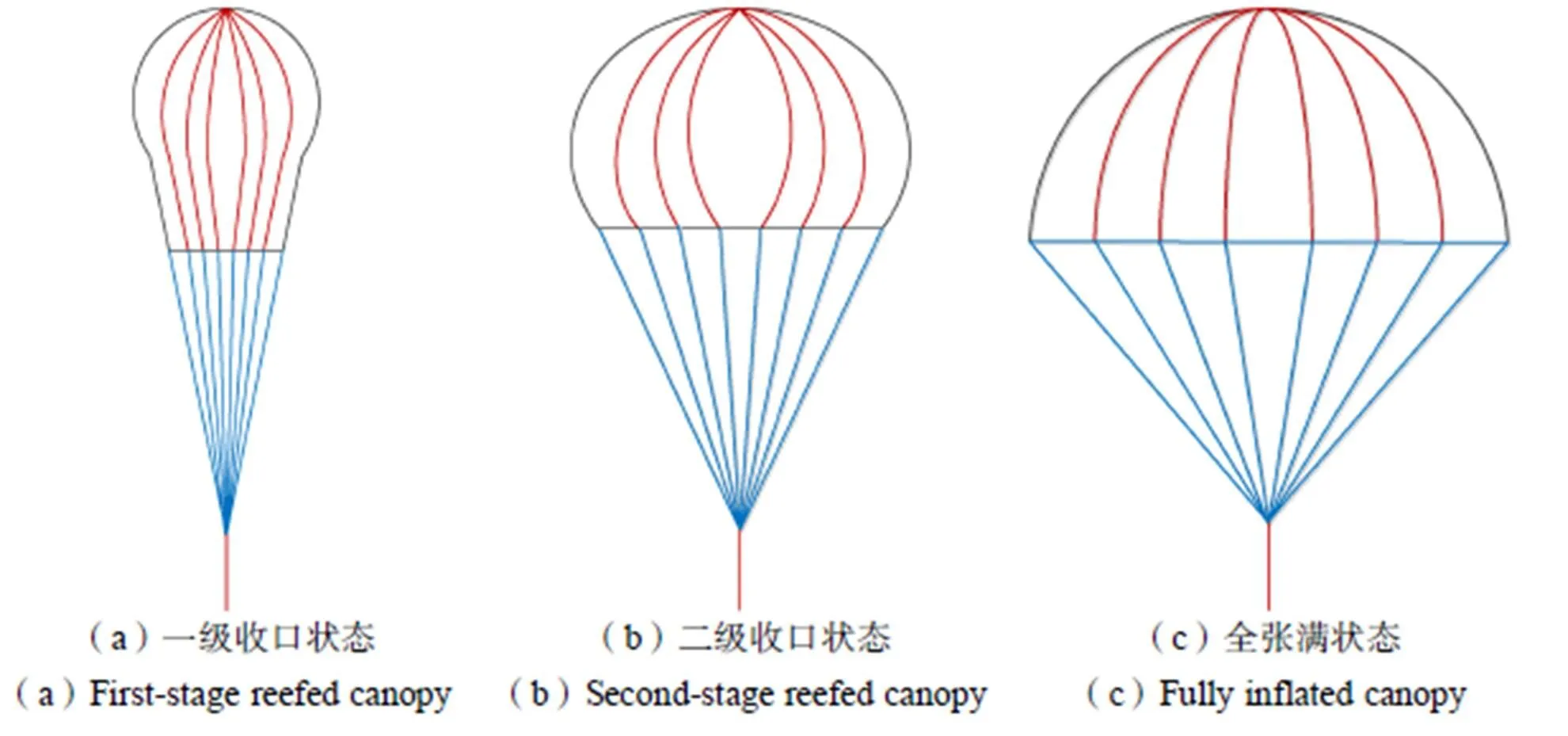
图1 一级收口、二级收口及全张满伞衣示意图
由于减速伞由柔性织物材料构成的特殊性,其减速伞气动外形在不同工作阶段差异显著,研究其瞬时动态特性较为困难,但在收口保持和充气张满阶段,气动外形及阻力特性较为稳定。目前应用于减速伞气动特性研究的数值方法主要有工程试验计算法[1-2]和数值模拟法[3],其中减速伞流场模拟采用涡动力方程[4]、雷诺平均Navier-Stokes方程[5]、大涡模拟(LES)等方法,这几种方法也代表了计算流体力学方法的最新技术发展。其中,LES方法更适用于求解减速伞流场,但相较于另两种方法对计算资源需求大幅提高。在减速伞动态流固耦合计算领域,一类常用方法为适用质量弹簧阻尼模型(Mass-Spring-Damper,MSD)对伞结构模型进行简化[6-8],同时引入减速伞附加质量[9]后对系统的动力学特性进行分析;另一类则基于有限元方法对伞结构进行离散化后进行结构场求解[10-11],而流场则采用低速不可压N-S方程进行求解[12],其中尤以DSD-SST模拟方法为代表[13-14]。近年来国内相关高校和研究机构在减速伞流固耦合数值仿真方面的研究也取得了丰硕成果,如文献[15-16]利用ALE方法对折叠状态的减速伞进行了无限质量条件下的充气展开仿真;文献[17]基于LS-DYNA软件进行了减速伞充气过程仿真研究,探究了减速伞充气时间与投影面积的变化规律;文献[18]对有限质量条件下的减速伞开伞过程进行了仿真,考察了投放速度对开伞时间和阻力面积的影响。
在减速伞风洞试验方面,文献[19-20]对“海盗号”减速伞的1/10缩比伞进行了伞衣面压力和阻力特性的测量。文献[21]对不同结构透气量的带条伞进行了阻力特性及充气过程气动外形的测量,考察了不同动压对减速伞开伞过程的影响。
对于减速伞收口状态的气动特性研究,目前多见于利用流固耦合方法进行数值分析,如文献[22]对猎户座飞船主伞进行了解除收口过程的动态模拟。
本文针对某型减速伞建立了流场仿真模型,分析了减速伞收口状态的阻力特性。同时,通过与风洞试验结果的对比,对风洞阻塞比引起阻力面积实验结果偏大的机理进行了探讨。
1 数值仿真
1.1 流场控制方程及建模
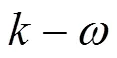

式中为流场守恒变量;为时间;为流场单个网格控制体单元体积;为控制体单元边界;为单元边界法向单位向量。式(1)左端第一项为守恒变量时间导数项,第二、三项分别为无粘项和粘性项。c和A分别为穿过控制体单元边界的无粘和粘性通量向量。
计算和试验所用的带条型减速伞模型及其周围的混合式流场网格如图2所示,建模时伞衣采用了1∶1真实模型,稳态计算中所使用的伞衣气动外形由先期基于LS-Dyna软件的流固耦合计算得出,随后利用Catia进行曲面修复,确保每个伞衣幅面由单个光滑曲面构成。伞衣底边曲线由三次样条曲线拟合而成(采样点不小于7个)。生成单幅伞衣后通过环形阵列构建整个伞衣表面。模型中仅包含伞衣面、径向带、顶孔加强带、伞衣底边带等各种绳带简化为线单元,在三维流场计算中不起作用,在计算中引入以下三个假设:

图2 减速伞模型俯视图及其周围网格示意图
1)伞衣面视为无透气性、无厚度壳单元;
2)忽略伞绳的气动力影响;
3)认为伞衣在充满至一级收口状态时伞内压力均匀分布,即伞衣沿中轴为周期对称模型。

利用基于时均化N-S方程的有限体积法进行空间离散及通量计算,求解器选择ANSYS CFX Solver进行计算。流场边界条件包括速度入口、来流动压出口以及四周开放式边界条件;由于本算例无需考虑伞衣的气动热效应,则伞衣表面采用无滑移绝热壁边界。图3所示为数值模拟的流场边界示意图。由于减速伞实际工作状态为无限空间,因此四周采用开放式远场边界。不同于其他外形规整的飞行器,减速伞的气动外形由成百上千个曲面构成,创建其周围的结构化网格极其困难。为节省计算时长,流场网格采用结构/非结构网格混合形式。本文采用在减速伞周围建立包络流场交界面的形式将流场分隔为内外两部分,贴近伞衣的区域采用四面体非结构网格,外围采用六面体结构化网格,将流场网格单元总数由全非结构网格的1 362万减少至混合网格的343万,且伞衣周围的流场网格品质并无下降。图4所示为二级收口状态的减速伞稳态流场速度云图。

图3 减速伞流场边界条件示意图

图4 来流90m/s、攻角0°工况下减速伞速度云图
1.2 计算结果
经过300步的迭代求解,流场控制方程的均方根残差收敛至10–6以下,流动趋于稳定,减速伞的阻力面积无明显变化,在此过程中流场残差的收敛曲线如图5所示,二级收口状态的阻力面积收敛曲线如图6所示。由图可见:减速伞在二级收口状态下的阻力面积为12.9m2。
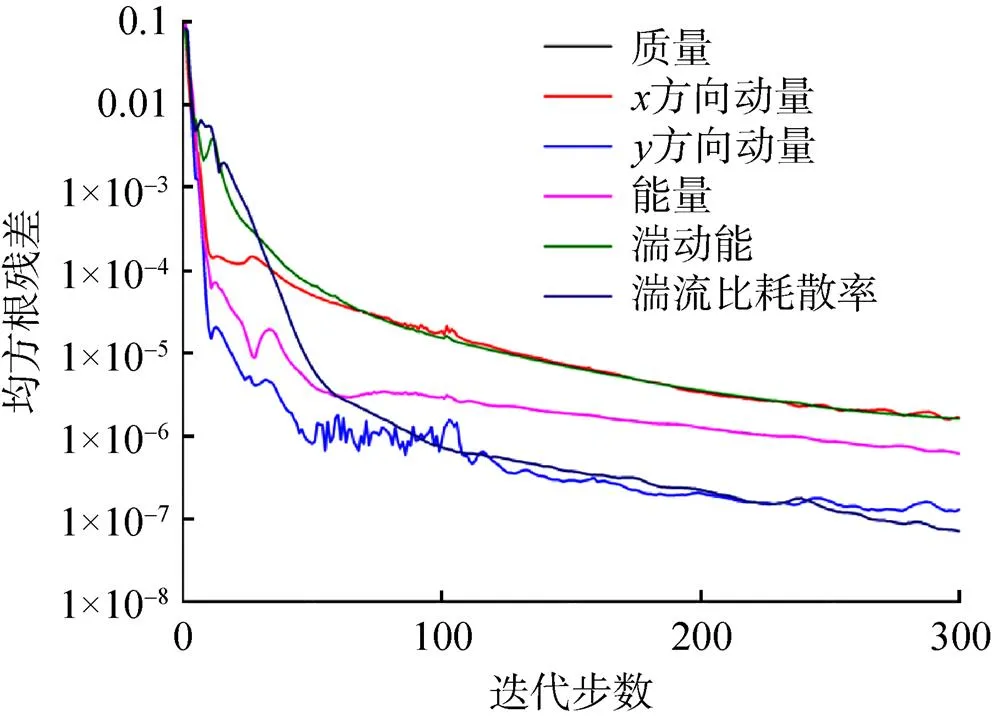
图5 流场变量残差收敛曲线

图6 减速伞二级收口状态阻力面积收敛曲线
2 风洞试验
2.1 实验装置
本次试验的主要目的为在预定动压工况下准确测量减速伞在一级及二级收口状态下的阻力面积,试验使用风洞为中国航空工业集团空气动力研究院的FL-10低速风洞。通过测量动压及风洞天平拉力,得到减速伞一级收口和二级收口状态的气动阻力,计算获得减速伞一级收口和二级收口的阻力面积,以及一级充气和二级充气的动载系数。试验风速为90m/s,对应的动压约为4 800Pa(按照风洞最大能力实施)。试验时减速伞呈包装状态置于伞包内,伞包放置于伞舱工装内,当风洞动压达到4 800Pa时,减速伞伞包从伞舱中被拉出,并快速充气至一级收口状态,一段时间后一级收口状态解除,减速伞充气至二级收口状态。图7所示为风洞试验装置布置示意图。试验分为稳态及动态两个工况,稳态工况目的为测量减速伞在二级收口状态下的阻力面积及气动阻力;动态工况目的为测量减速伞从一级收口状态变化至二级收口状态过程中阻力面积及气动阻力的变化。

图7 风洞试验装置布置示意图
2.2 风洞试验结果
稳态工况时,当风洞流动达到稳态时,动压d=4 824Pa,此时测得的减速伞阻力面积c=16.2m2。 图8所示为稳态试验过程中减速伞阻力面积及动压随时间的变化曲线。

图8 稳态试验减速伞阻力面积及风洞动压随时间变化曲线
如图9所示,动态工况中,当风洞流动达到初始稳定状态时动压为4 560Pa(如图10所示),减速伞充气至一级收口过程中最大开伞力为22.8kN。充气至二级收口状态过程中最大开伞力为53.9kN。流场稳定后,减速伞在二级收口状态下的气动阻力为37kN。如图11所示,减速伞的一级收口阻力面积为5.2m2,二级收口阻力面积为16.1m2。

图9 减速伞气动阻力随时间变化曲线

图10 动态试验风洞动压随时间变化曲线
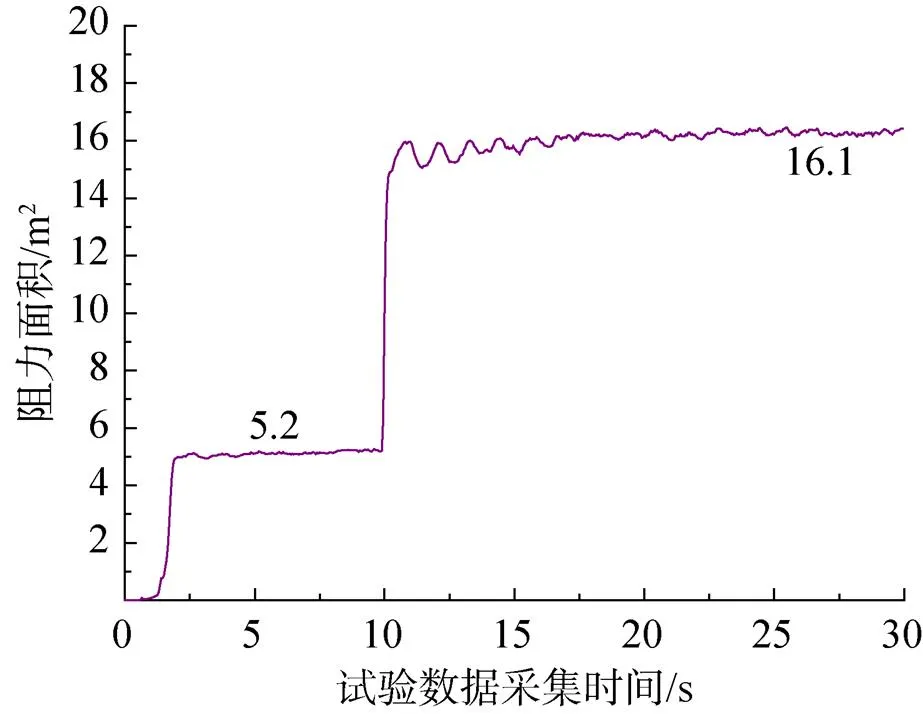
图11 动态试验减速伞阻力面积随时间变化曲线
3 计算及试验结果对比分析
前文所述稳态数值计算针对二级收口状态的减速伞,一级收口状态时风洞试验可明显观察到底边附近伞衣抖动明显。图12为风洞试验和仿真计算的阻力面积随时间变化曲线,可见试验测得的阻力面积数值在5.7m2上下波动,仿真结果的阻力面积时均值为4.82m2。
由表1所示的风洞试验实测数据可见:测得的减速伞各级阻力面积均大于仿真值,通过一些文献调研,分析原因认为:减速伞张开后在风洞中的阻塞效应非常明显,因此采用式2所示的简单修正公式[23-24]:
式中D为实测阻力系数;D,c为修正后阻力系数;为实测减速伞阻力面积,c为修正后阻力面积;p为物体流线方向的投影面积;为风洞的横截面积;约为5/2,其变化很小。阻力面积同样有以上关系式,在一级收口阶段,/c=1.212;在二级收口阶段,/c=1.297。经过修正后的风洞试验结果如表1所示:
并且,对于表1中稳态试验与动态试验测得的减速伞一级收口阻力面积不一致问题,认为原因如下:
稳态试验中采集的是风洞内部流场达到非常稳定后的数据,此时,风洞内的流动近似为稳态流场;而动态试验中,减速伞从拉出、充气至一级收口状态到解除一级收口,仅有8s时间。这一系列过程中伞系阻力面积突变造成风洞内流场随之变化,并且风洞为回流式风洞,在短时间内风洞流场来不及建立平衡,由图11可见,在减速伞一级收口至二级收口状态之间的8s其阻力面积一直在缓慢增加。因此认为稳态试验的5.7m2作为测试结果进行分析更为准确,经过修正后阻力面积为4.7m2。减速伞的二级收口阻力面积实测结果为16.2m2,修正后平均阻力面积为12.5m2。且不同动压下的动态试验测得的减速伞阻力面积具有一致性。
表1 风洞实测及修正后数据

Tab.1 Original and correctional data of wind tunnel tests
4 结束语
本文使用数值仿真方法对某减速伞的两级收口状态阻力特性进行了预测,并通过风洞试验对减速伞在稳态和动态解除收口过程中的阻力特性进行了测试。仿真计算与实验结果对比表明,数值分析手段能够较为准确的预测减速伞的稳态气动特性。同时,通过对风洞试验中存在的减速伞阻塞比过大问题进行分析,在试验数据修正方面进行了探讨。仿真与试验相结合的方法能够有效可行地对减速伞的动静态特性进行预估分析,为减速伞设计提供重要的参考依据。
[1] TEZDUYAR T, OSAWA Y, STEIN K, et al. Computational Methods for Parachute Aerodynamics[M]//Computational Fluid Dynamics for the 21stCentury. Springer Berlin Heidelberg, 2001.
[2] JAMES J H, MACHA J M. Preliminary Characterization of Parachute Wake Recontact[J]. Journal of Aircraft, 1990, 27(6): 501-506.
[3] JOHARI H, DESABRAIS K J. A Coupled Fluid-structure Parachute Inflation Model[C]//17th AIAA Aerodynamic Decelerator Systems Technology Conference and Seminar. Monterey, USA, 2003.
[4] JOHARI H, STEIN K, TEZDUYAR T. Impulsively Started Flow About a Rigid Parachute Canopy[J]. Journal of Aircraft, 2001, 38 (6): 102-109.
[5] DESABRAIS K J, JOHARI H. Near-field wake of a generic, round parachute canopy in steady flow[C]//39th AIAA Aerospace Sciences Meeting and Exhibit, Reno. USA, 2001.
[6] SUNDBERG W D. New Solution Method for Steady-state Canopy Structural Loads[J]. Journal of Aircraft, 1988, 25(11): 1045-1051.
[7] 朱勇, 刘莉. 基于拉格朗日力学的伞-弹系统动力学模型[J]. 航空学报, 2009, 30(7): 1208-1213. ZHU Yong, LIU Li. Dynamic Model of Parachute-projectile Systems Based on Lagrange Mechanics[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(7): 1208-1213. (in Chinese)
[8] 朱旭, 曹义华. 翼伞平面形状对翼伞气动性能的影响[J]. 航空学报, 2012, 32(11): 1998-2007. ZHU Xu, CAO Yihua. Numerical Simulation of Planform Geometry Effect on Parafoil Aerodynamic Performance[J]. Acta Aeronautica et Astronautica Sinica, 2012, 32(11): 1998-2007. (in Chinese)
[9] 黄伟. 降落伞附加质量的计算方法[J]. 航天返回与遥感, 2016, 37(2): 42-50. HUANG Wei. Calculation Methods of Added Mass of Parachute[J]. Spacecraft Recovery & Remote Sensing, 2016, 37(2): 42-50. (in Chinese)
[10] STEIN K, TEZDUYAR T E, BENNEY R. Computational Methods for Modeling Parachute Systems[J]. Computing in Science and Engineering, 2003, 5(1): 39-46.
[11] BENNEY R, LEONARD J. A 3-D Finite Element Structural Parachute Model[C]//Proceedings of the 13th AIAA Aerodynamic Decelerator Systems Technology Conference. Florida, USA, 1995.
[12] TEZDUYAR T E. Stabilized Finite Element Formulations for Incompressible Flow Computations[J]. Advances in Applied Mechanics, 1991, 28(1): 1-44.
[13] TAKIZAWA K, SPIELMAN T, TEZDUYAR T E. Fluid-structure Interaction Modeling of Ringsail Parachute Clusters[C]//Recent Progress on Fluid Dynamics Research, Proceeding of the International Conference on Fluid Mechanics, Guangzhou, China, 2011.
[14] TAKIZAWA K, FRITZE M, MONTES D, et al. Fluid–structure Interaction Modeling of Ringsail Parachutes with Disreefing and Modified Geometric Porosity[J]. Computational Mechanics, 2012, 50(6): 835-854.
[15] 陈猛, 王璐, 程涵. 降落伞充气过程流固耦合方法的数值预测分析[J]. 南京航空航天大学学报, 2013, 45(4): 20-25. CHEN Meng, WANG Lu, CHENG Han. Numerical Prediction Analysis of Parachute Inflation Process Using Fluid-Structure Interaction Method[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(4): 20-25. (in Chinese)
[16] 程涵, 余莉, 李胜全. 基于ALE的降落伞充气过程数值仿真[J]. 南京航空航天大学学报, 2012, 44(3): 290-293. CHENG Han, YU Li, LI Shengquan. Numerical Simulation of Parachute Inflation Process Based on ALE[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2012, 44(3): 290-293. (in Chinese)
[17] 贾贺, 荣伟, 陈国良. 基于LS-DYNA软件的降落伞充气过程仿真研究[J]. 航天器环境工程, 2010, 27(3): 367-373. JIA He, RONG Wei, CHEN Guoliang. The Simulation of Parachute Inflation Process Based on LS-DYNA[J]. Spacecraft Environment Engineering, 2010, 27(3): 367-373. (in Chinese)
[18] 高兴龙, 张青斌, 高庆玉. 有限质量降落伞充气动力学数值模拟[J]. 国防科技大学学报, 2016(4): 185-190. GAO Xinglong, ZHANG Qingbin, GAO Qingyu. Numerical Simulation on Finite Mass Inflation Dynamics of Parachutes[J]. Journal of National University of Defense Technology, 2016(4): 185-190.(in Chinese)
[19] STEINBERG S Y, SIEMERS P M, SLAYMAN R G. Development of the Viking Parachute Configuration by Wind-Tunnel Investigation[J]. Journal of Spacecraft and Rockets, 1974, 11(2): 101-107.
[20] WITKOWSKI A, KANDIS M. Reefing the Mars Science Laboratory parachute[C]//Aerospace Conference. IEEE, Montana, USA, 2010.
[21] PEPPER W B, REED J F. Parametric Study of Parachute Pressure Distribution by Wind Tunnel Testing[J]. Journal of Aircraft, 1976, 13(11): 895-900.
[22] TAKIZAWA K, TEZDUYAR T E, BOSWELL C, et al. FSI Modeling of the Reefed Stages and Disreefing of the Orion Spacecraft Parachutes[J]. Computational Mechanics, 2014, 54(5): 1203-1220.
[23] 顾明, 黄剑. 建筑模型风洞试验阻塞效应研究进展[J]. 同济大学学报(自然科学版), 2016, 44(1): 1-10. GU Ming, HUANG Jian. Research Progress of Wind Tunnel Blockage Effects on Building Models[J]. Journal of Tongji University (Natural Science), 2016, 44(1): 1-10. (in Chinese)
[24] 黄剑, 顾明. 群体高层建筑模型风洞试验阻塞效应的修正[J]. 同济大学学报(自然科学版), 2017(1): 35-42. HUANG Jian, GU Ming. Blockage Correction of Group Tall Building Models in Wind Tunnel Test[J]. Journal of Tongji University (Natural Science), 2017(1): 35-42.
Numerical Simulation and Experimental Study on Aerodynamic Characteristics of Reefed Decelerating Parachute
WANG Qi1,2WANG Liwu1,2ZHANG Zhang1,2WU Zhuo1,2LEI Jiangli1,2SUN Xiyun1,2
(1 Beijing Institute of Space Mechanics & Electricity, Beijing 100094, China (2 Key Laboratory for Nondestructive Spacecraft Landing Technology of CAST, Beijing 100094, China)
Decelerating parachute is an important pneumatic instrument of the recovery landing system. Aerodynamic characteristics determine the success or failure of the whole deceleration and landing process. Because of the high opening dynamic pressure and payload, design of the aerodynamic configuration is an emphasis. In addition, to reduce the dynamic load during the opening process, the skirt of canopy is generally controlled to achieve gradual expansion. The decelerating parachute described in this paper has a two-stage reefed configuration. In this paper, research of numerical simulation and wind tunnel test on the decelerating parachute with striped canopies in reefed state are carried out. The aerodynamic shape of decelerating parachute in the typical stages of opening procedure is obtained by using the fluid-structure coupling method, and the aerodynamic performance in the critical states of liberalizing reefed parachute are calculated and analyzed utilizing CFD method. Simultaneously, to investigate the static drag in the reefed stages and its variation of the decelerating parachute during the process of deployment, and to verify the working reliability of the reefing device, steady and dynamic tests are implemented in a subsonic wind tunnel, and drag area and dynamic characteristics of the parachute are measured. The experimental results show that the simulation can accurately predict the aerodynamic and dynamic characteristic of the parachute of reefed state with error less than 5%, and can provide an important basis for structure and strength design.
numerical simulation; wind tunnel test; reefed decelerating parachute; dynamic characteristics; space re-entry
V211.3
A
1009-8518(2019)03-0024-09
10.3969/j.issn.1009-8518.2019.03.004
王奇,男,1985年生,2016年获南京航空航天大学测试计量技术及仪器专业博士学位,工程师。研究方向为回收着陆系统动力学及气动减速数值分析。E-mail:woshiiory@126.com。
2019-04-03
国家重大科技专项工程
(编辑:刘颖)
———重庆建成世界一流汽车风洞

