基于扩展卡尔曼滤波的星敏感器在轨几何标定
李响 谢俊峰,* 莫凡 朱红 金杰
基于扩展卡尔曼滤波的星敏感器在轨几何标定
李响1谢俊峰1,2*莫凡2朱红2金杰1
(1 辽宁工程技术大学测绘与地理信息学院,阜新 123000) (2 自然资源部国土卫星遥感应用中心,北京 100048)
星敏感器在轨几何标定是消除其系统测量误差,提高姿态确定精度的有效手段之一。目前利用星对角距相等进行星敏感器在轨标定时,大多采用最小二乘求得全局最优的静态待标定参数,但没有完全反映出恒星相机工作期间受外太空环境变化导致内部参数发生的微小动态变化。为了进一步提高星敏感器参数的在轨标定精度,文章在对星图识别结果预处理的基础上,引入扩展卡尔曼滤波对当前星图时刻对应的相机参数进行实时标定,动态获取当前最优参数值。利用该文所提方法对“资源三号”01/02星国产星敏感器进行在轨标定,试验结果表明所提方法能够有效标定当前星敏感器的参数误差,其精度优于传统的最小二乘标定方法,验证了该方法具有更好的适应性和可靠性,为星敏感器的在轨几何标定提供了一种技术参考,可用于卫星在轨实时标定或地面卫星姿态后处理。
扩展卡尔曼滤波在轨标定星敏感器高分辨率对地观测 遥感相机
0 引言
随着高分辨率遥感卫星应用深入,用户对卫星姿态测量精度提出了更高的要求。星敏感器作为当前绝对定姿精度最高的测量设备,成为高分辨率对地观测卫星必备的重要载荷,其测量精度直接关系到用户产品的几何精度[1]。由于卫星发射过程振动、太阳光辐射引起的温度变化等,致使星敏感器光学镜头的焦距、主点偏移等内部参数出现系统偏差、严重影响了星敏感器的定姿精度[2]。因此,为了消除其系统误差影响,星敏感器在轨标定是实现星敏感器姿态测量必不可缺少的环节之一。
针对星敏感器在轨标定方法国内外学者开展了很多研究[3]。标定方法大致可分为三类:第一类方法是采用最小二乘(Least squares,LS)对星敏感器主距、主点等系统参数进行标定[5-8]。第二类方法是采用扩展卡尔曼滤波(Extended Kalman Filtering,EKF)对在轨星图进行处理,得到当前星图所对应的内部参数[9]。前两类方法均是基于星像点计算的星对角距与导航星表计算的星对角距相等的原理进行标定,区别在于两者的解算策略不同。第三类方法是通过空间后方交会的原理进行在轨标定,需要在标定内参数同时修正姿态外参数,文献[10-12]在此方法基础上选取星像点分布均匀的星图数据进一步提升标定 精度。
考虑到算法可靠性与实时性要求,当前在轨实际应用主要采用算法简单可靠的第一类方法,通过系统标定后得到一组全局最优的标定参数。然而,实际上星敏感器在轨工作过程中,太空环境因素的变化会引起内部参数的缓慢变化,星像点提取算法中存在提取误差,其内参数解算的值会以真实值为基础上下波动。采用最小二乘法解算的全局最优静态参数无法表征局部内参数变化信息;而扩展卡尔曼滤波法对每幅星图都有其对应的内参数解,能够直观体现出内参数的实时变化信息,应用此方法进行星敏感器标定可以更好的表示变化的规律,应用于星敏感器在轨标定中,可以实时的获得当前状态的内参数值,得到更高精度的姿态值。目前,国内学者基于扩展卡尔曼滤波法进行标定研究,仅仅开展仿真试验验证,收敛速度较慢,依赖星图数据较多。本文在此算法的基础上,对基于扩展卡尔曼滤波进行星敏感器标定的算法的收敛速度进行了优化。利用“资源三号”01/02星国产星敏感器下传在轨星图进行试验验证,对试验数据预处理之后[13],通过与最小二乘的结果进行精度对比,利用星内角统计偏差进行评价[14],进一步验证了算法的可靠性和实用性。

图1 星敏感器小孔成像模型
1 星对角距相等原理
星敏感器成像的理想模型是小孔成像模型[15],如图1所示,星光透过光学系统在星敏感器成像元件上形成弥散斑,根据理想的小孔成像模型,星敏感器得到的测量星向量和星库星向量之间有一一对应关系,但是由于星敏感器参数改变,使得这种对应关系出现偏差。
图1中,CISCISCIS坐标系是以地球质心为原点,CIS轴与CIS轴分别指向2000年1月1日12时的北极点、春分点,CIS轴按右手规则确定的J2000协议惯性坐标系(Conventional inerial system),每颗星在星表中有唯一的方向矢量,即
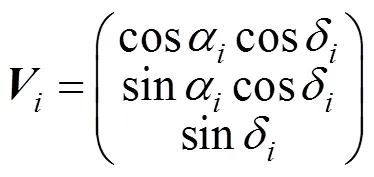
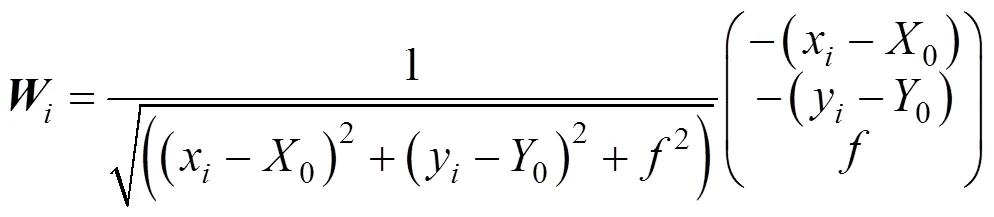



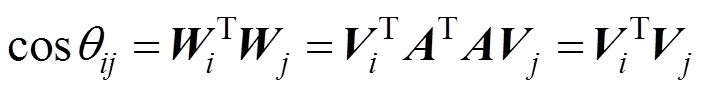
2 基于扩展卡尔曼滤波法的星敏感器在轨标定
扩展卡尔曼滤波法是一种广泛应用的非线性系统滤波方法[16],能够对星点的随机误差进行处理,其本质上是一种递归算法[17]。星敏感器在轨几何标定是建立在星像点计算的星对角距与导航星表计算的星对角距相等的基础上,对每一幅星图进行一次递归运算,得到当前星图所对应的标定参数。根据卫星实际在轨状态,星敏感器内参数短期变化较小,扩展卡尔曼滤波状态方程如公式(5)所示
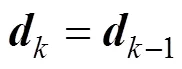
由公式(4)可得
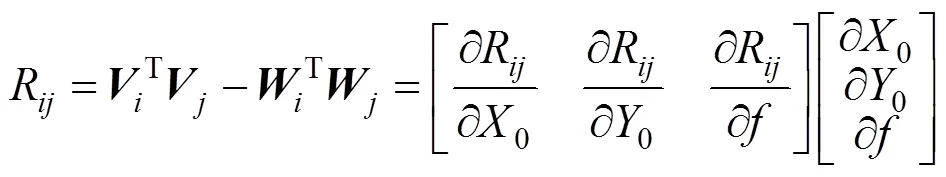
式中R为序号为的星和序号为的星之间的星对角距的余弦值之差,理论值为0。

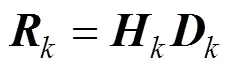

一般情况下,扩展卡尔曼滤波收敛速度较慢。本文为了加快收敛速度,对影响收敛因素进行分析并加以改进[18]。
具体步骤如下:
1)为了避免星像点质心提取粗差对标定精度的影响,确保标定方法验证的可靠性,对星图识别结果进行预处理,剔除误差较大试验数据。预处理过程需要去除粗差点与星像点不足的星图。考虑到当前质心提取算法精度达到子像素级,假定本试验质心提取误差为0.5个像素,则可以容许的星对角距误差阈值(单位:角秒)为
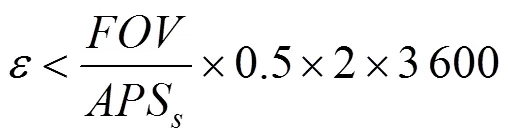
式中 FOV代表视场角大小;APSS代表星敏感器面阵大小。
3)读取一幅星图中星点的像点坐标以及赤经、赤纬;根据公式(7)计算卡尔曼滤波量测方程的观测变量以及系数矩阵。
4)计算卡尔曼滤波增益为
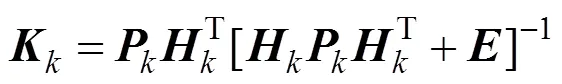
式中为星敏感器的测量噪声方差强度阵。
5)由观测变量更新为




8)计算下一张星图的协方差矩阵以及重置+1,返回步骤2)

式中是单位矩阵。
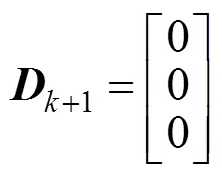
基于扩展卡尔曼滤波对星敏感器标定流程如图2所示。

图2 基于扩展卡尔曼滤波的标定流程图
3 试验分析与验证
3.1 试验数据与预处理
(1)试验数据
2012年1月9日,“资源三号”01星在太原卫星发射中心成功发射[19],主要用于1:5万比例尺立体测图[20],为满足“资源三号”卫星高精度有/无控制定位精度[21]的工程研制要求,卫星搭载3台星敏感器,其中2台为德国的ASTRO-10星敏感器,另外一台是北京控制工程研究所研制的APS星敏感器,为国内星敏感器首次具备下传对地相机成像时段的原始星图的星敏感器。“资源三号”02星于2016年5月30日在太原卫星发射中心成功发射并进入预定轨道,与“资源三号”01星组网运行。02星星敏配置与01星一样。本文主要采用01/02星国产星敏感器下传的原始星图作为试验数据,国产星敏感器的基本技术参数如表1所示。
表1 ZY-3 01/02 APS星敏感器基本参数
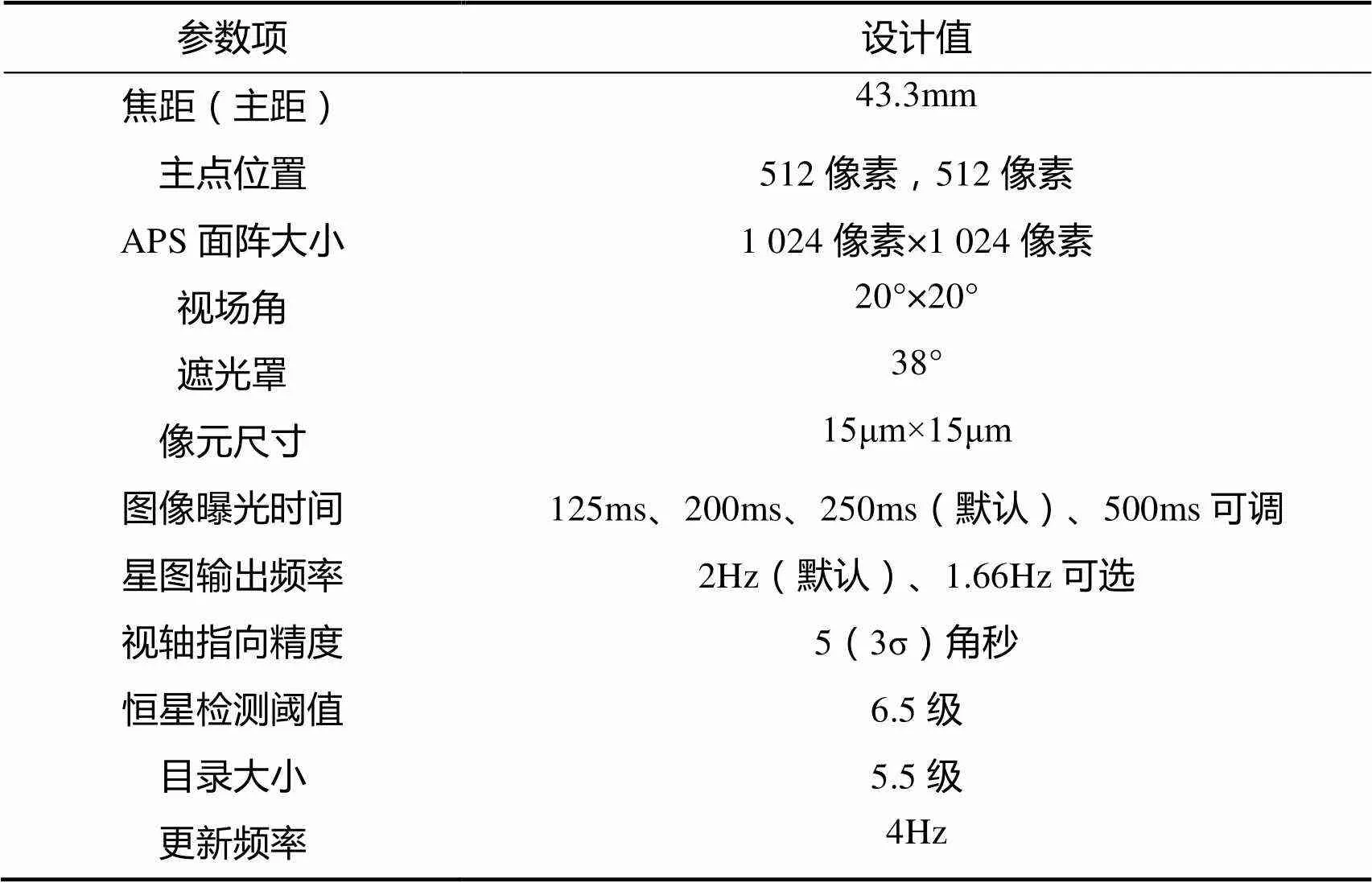
Tab.1 ZY-3 01/02 basic parameters of APS star tracker
为验证算法的可靠性和普适性,试验选取“资源三号”01星与02星发射初期下传的三轨星图,如表2所示。随机挑选一轨数据中的某一帧原始星图如图3所示。
表2 试验数据

Tab.2 Test data

(获取时间:2012-02-03 11:15:54.182702)
图3为星敏下传的原始星图,含有背景噪声,图中的红圈圈起来的光亮点代表所拍摄到的恒星中能量值较高的点,星图中含有大量的非均匀性噪声,如星图中心区域与边缘区域(区域①、②)的曝光强度不同,垂直方向上存在明显的条带,这些非均匀性噪声基本可以认定为系统噪声。
(2)预处理
剔除粗差点,此类像点与其遍历的其它像点所计算出的星对角距都大于阈值。根据表1所示的视场角与星敏感器面阵大小以及公式(8)求出此试验可以容许的星对角距误差阈值为70.312 5″。
对星图像点进行粗差剔除后,会出现少量星图中星像点低于两个的情况,为了保证算法的完整性,该星图不作为试验数据。对恒星影像预处理后,用于标定的试验数据包含星图数目、星像点个数、星像点坐标以及赤经、赤纬等信息,其中恒星的像点坐标表示此恒星在以星图像主点为原点的像平面坐标系下的坐标。其单幅星图中星点信息如表3所示。
表3 数据预处理(以381轨为例)
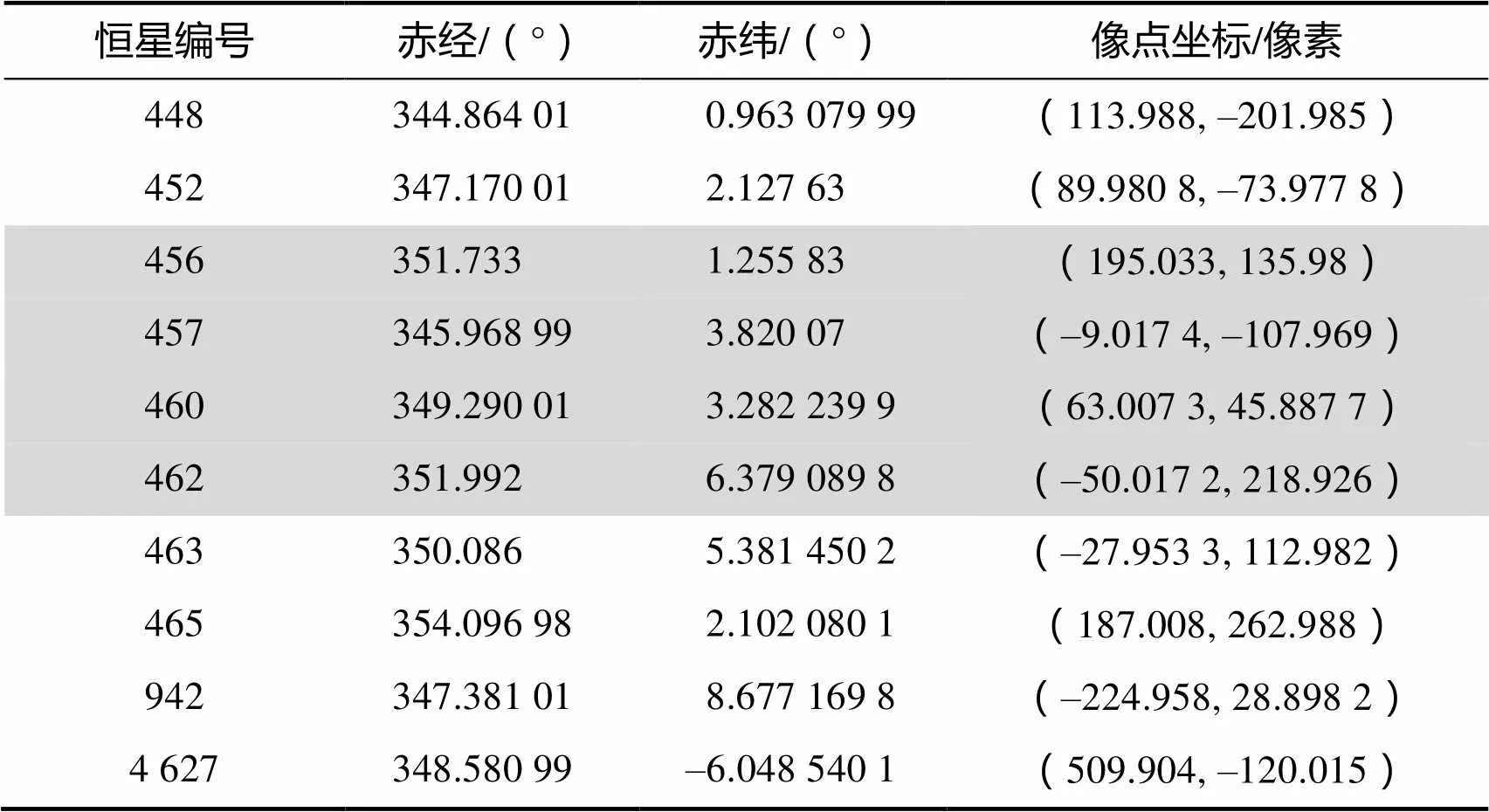
Tab.3 Pre-processing of data(381th Track)
注:表格中灰色部分为需要剔除的粗差点。
3.2 试验结果分析
(1)标定结果
本试验的三轨数据在进行剔除粗差点与星图后,星图数目都有减少,其中,第381轨作为试验数据的星图数为110景,第216轨作为试验数据的星图数为550景,第417轨作为试验数据的星图数为190景。
采用扩展卡尔曼滤波对标定参数主距、主点进行解算,为了反映迭代过程中参数的变化情况,本试验同时给出了基于最小二乘法标定结果。为了满足尽快收敛的需求,在设定的初始的协方差矩阵时,使其尽可能大。利用三轨数据进行扩展卡尔曼滤波标定的结果分别如图4、5、6所示。

图4 381轨标定结果

图5 216轨标定结果

图6 417轨星图迭代过程中参数变化
基于扩展卡尔曼滤波的星敏感器标定在内参数标定过程中,焦距的收敛性明显高于像主点,基本在100幅星图内即可收敛,像主点基本在200幅星图即可收敛。基于扩展卡尔曼滤波进行星敏感器标定的内参数最后都是收敛于最小二乘法解算出来的全局最优参数,并在收敛后基于此参数上下波动。可以看出,通过增大协方差的值来追求快速收敛的方法是可行的。
(2)标定精度分析
计算出各个星图的星内角距统计偏差值,对基于扩展卡尔曼滤波的星敏感器标定出来的内参数精度验证。
1)与初值对比。验证检校前后精度对比,采用检校前初值和检校后参数代入计算各个星图星内角距统计偏差,分别如图7、8、9所示。
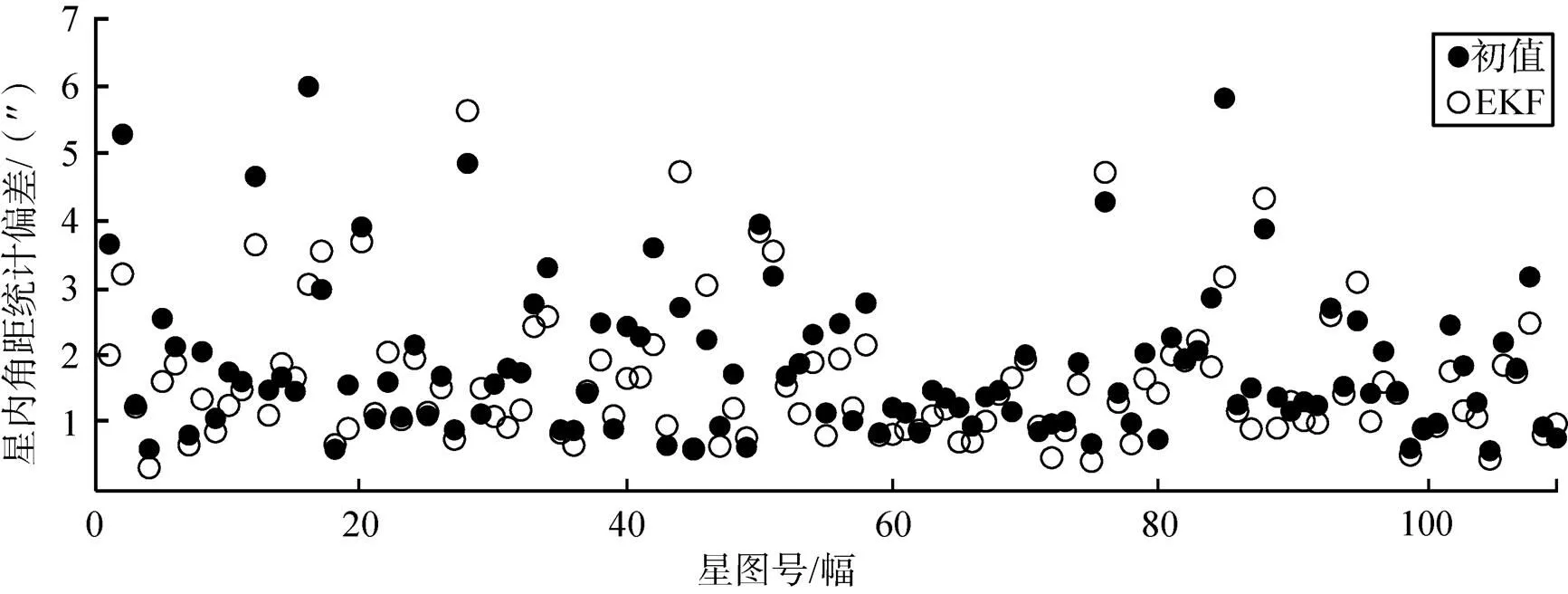
图7 第381轨星图星内角距统计偏差值
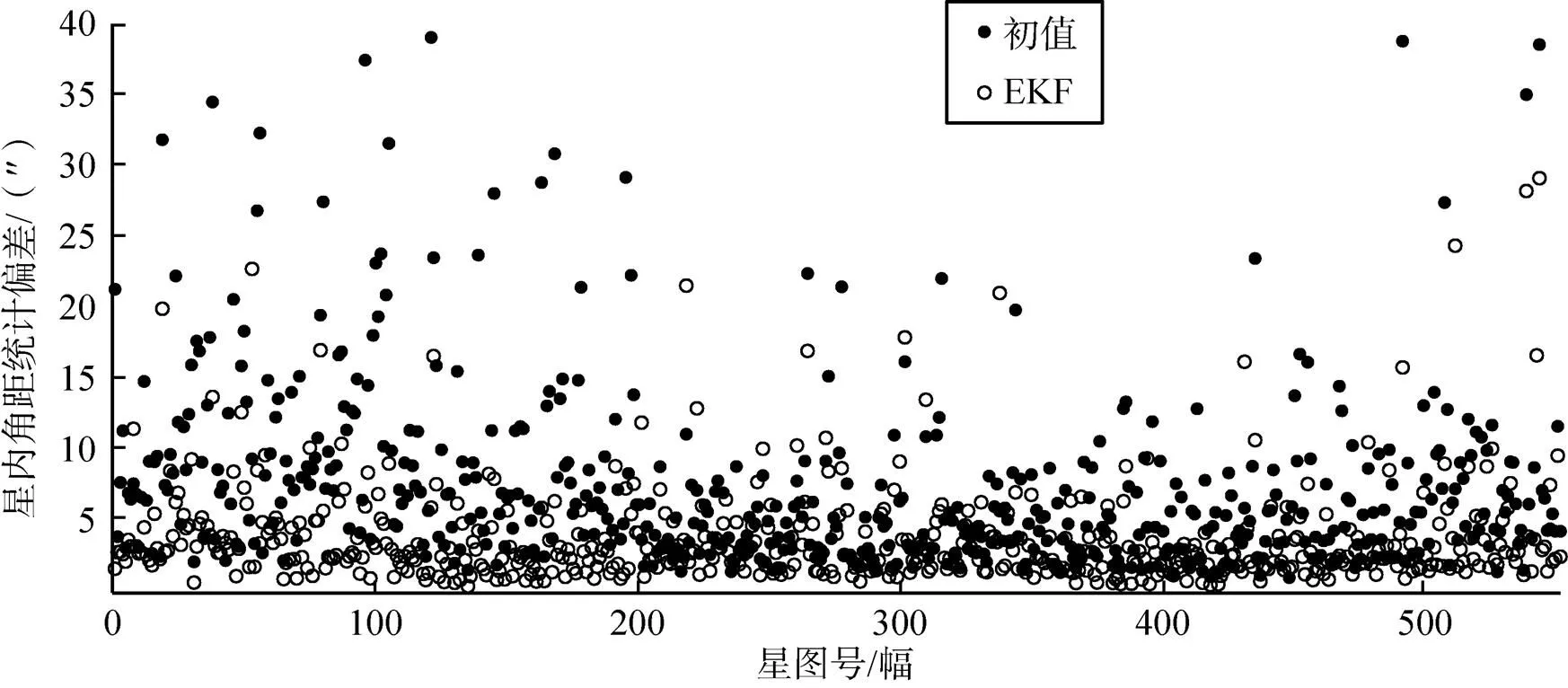
图8 第216轨星图星内角距统计偏差值

图9 第417轨星图星内角距统计偏差值
通过图7~图9可以直观看出,经扩展卡尔曼滤波标定后的星图星内角距统计偏差值明显小于初值的星内角距统计偏差值。
两种方法标定的参数与初始参数计算出的星内角统计偏差的平均值与标准差如表4所示。
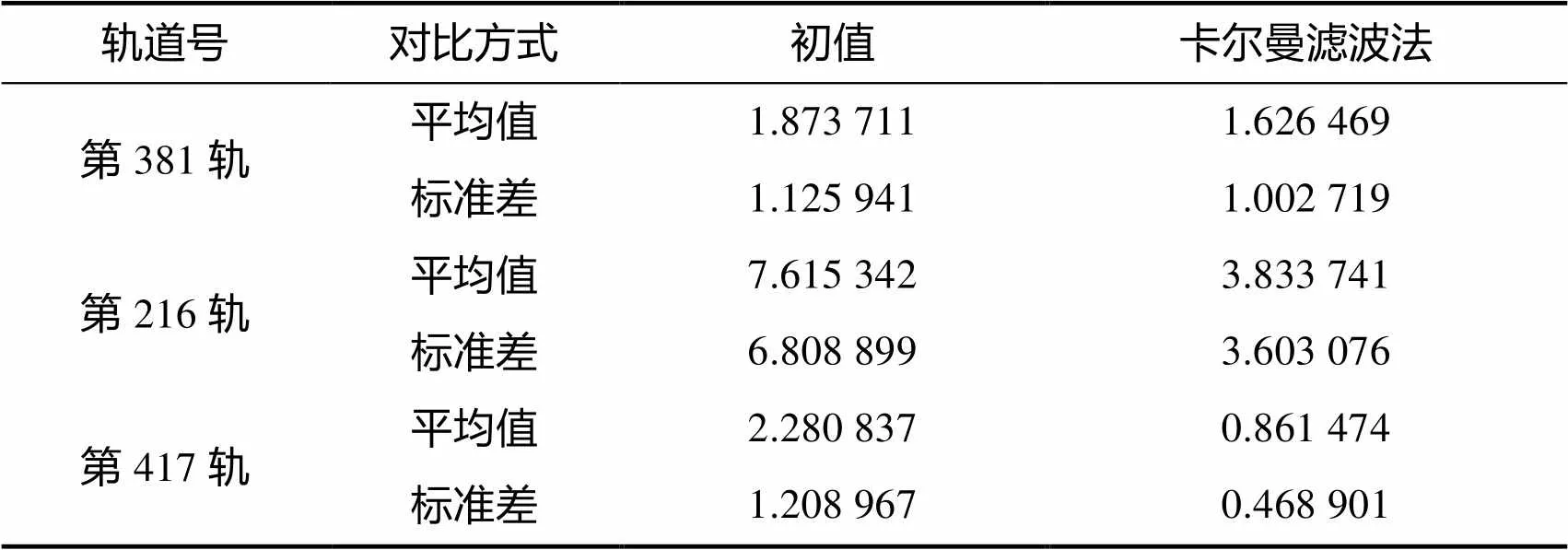
表4 星内角统计偏差对比
表4表明,与检校前相比,利用扩展卡尔曼滤波法标定后参数计算得到三轨星图角距差均值分别提高了0.247 242″、3.781 601″、1.419 363″,标准差也有明显的降低。
2)与最小二乘对比。对基于卡尔曼滤波标定过程内参数收敛之后的值与最小二乘得到的内参数的值求得星内角统计偏差,进行对比,如表5所示。
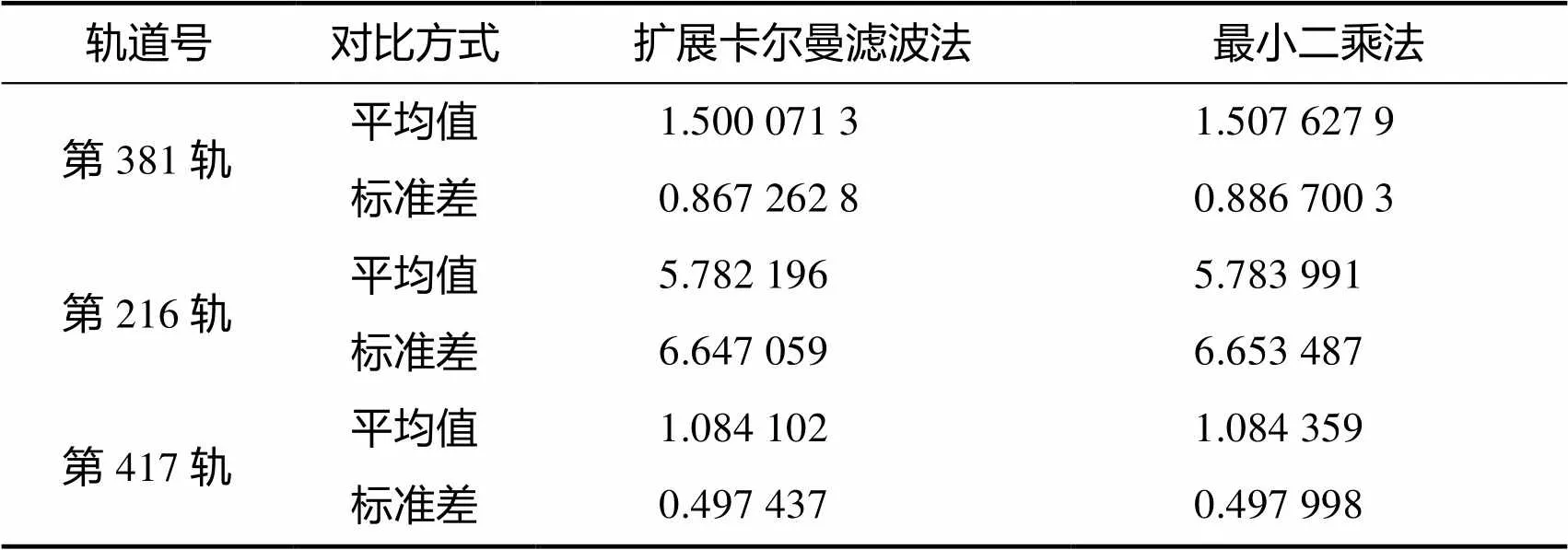
表5 收敛后的扩展卡尔曼滤波与最小二乘统计偏差对比
基于扩展卡尔曼滤波对星敏感器标定的方法,标定的结果对每一幅星图都有其对应的内参数,其内参数收敛后所求得的星内角统计偏差与最小二乘得到的内参数所求得的星内角统计偏差对比可以看出,基于扩展卡尔曼滤波解算的内参数在收敛后略优于基于最小二乘解算的内参数,其星内角统计偏差的平均值与标准差均略小于最小二乘法。考虑到本次试验的试验数据较少、拍摄时间较短,基于扩展卡尔曼滤波解算的方法相较于基于最小二乘解算的方法并没有明显的优势,但在星上需长期实时标定的情况下,精度上,扩展卡尔曼滤波在长时间的在轨运行中足以收敛,其精度将明显优于最小二乘法的精度。实时性上,最小二乘法需要得到该轨所有星图进行处理才可保证其精度,适用于事后处理。扩展卡尔曼滤波法可以做到每拍摄一张星图即可得到该星图内参数,适用于实时处理。
此方法应用于在轨星敏感器运行,可实时更正星敏内参数值,对单视场星敏(如“资源三号”系列卫星)可直接用于其在轨标定,对双视场星敏[22](即将发射的“高分七号”卫星),可以实时获取每个视场的内参数信息,得到更加精确的双视场旋转矩阵以及姿态信息[23]。
4 结束语
本文针对星敏感器系统测量误差的在轨几何标定,在星对角距相等原理的基础上,提出了一种基于扩展卡尔曼滤波的标定方法,同时详细阐述了星敏相机的标定技术流程。以“资源三号”01/02星国产星敏感器为试验载荷,验证了该方法能够有效标定星敏感器的参数误差,提高卫星姿态测量精度,较传统的最小二乘标定方法,更具有实时性,可以更好地应用到卫星在轨几何标定业务中。后续将针对多星敏感器或多头星敏感器在轨几何检校开展研究,进一步优化卫星姿态的测量精度。
[1] 袁彦红, 耿云海, 陈雪芹. 星敏感器自主在轨标定算法[J]. 上海航天, 2008(3): 6-10. YUAN Yanhong, GENG Yunhai, CHEN Xueqin. Autonomous On-obit Calibration of Star Sensors[J]. Aerospace Shanghai, 2008(3): 6-10. (in Chinese)
[2] 王晓东. 大视场高精度星敏感器技术研究[D]. 长春: 中国科学院研究生院(长春光学精密机械与物理研究所), 2003. WANG Xiaodong. Research on High-precision Star Sensor Technology for Large Field of View[D]. Changchun: Chinese Academy of Sciences (Changchun Institute of Optics, Fine Mechanics and Physics), 2003. (in Chinese)
[3] 梁斌, 朱海龙, 张涛, 等. 星敏感器技术研究现状及发展趋势[J]. 中国光学, 2016, 9(1): 16-29. LIANG Bin, ZHU Hailong, ZHANG Tao, et al. Research Status and Development Tendency of Star Tracker Technique[J]. Chinese Journal of Optics, 2016, 9(1): 16-29. (in Chinese)
[4] JU G. Autonomous Star Sensing, Pattern Identification, and Attitude Determination for Spacecraft: An Analytical and Experimental Study[D]. College Station, Texas: Texas A&M University, 2001.
[5] SAMAAN M A. Toward Faster and More Accurate Star Tracker Using Recursive Centroiding and Star Identification[D]. College Station, Texas: Texas A&M University, 2003: 25-29.
[6] 郝雪涛, 张广军, 江洁. 星敏感器模型参数分析与校准方法研究[J]. 光电工程, 2005, 32(3): 5-8. HAO Xuetao, ZHANG Guangjun, JIANG Jie. Star Tracker Model Parameter Analysis and Calibration Method[J]. Opto-electronic Engineering, 2005, 32(3): 5-8. (in Chinese)
[7] 刑飞, 董瑛, 武延鹏, 等. 星敏感器参数分析与自主校正[J].清华大学学报(自然科学版), 2005, 45(11): 1484-1488. XING Fei, DONG Ying, WU Yanpeng, et al. Star Tracker Parametric Analysis for Autonomous Calibration[J]. Journal of Tsinghua University (Science and Technology), 2005, 45(11): 1484-1488. (in Chinese)
[8] 谢俊峰, 龚健雅, 江万寿. 一种改进的恒星相机在轨检校方法[J]. 测绘科学, 2009, 34(2): 121-123. XIE Junfeng, GONG Jianya, JIANG Wanshou. An Improved On-orbit Calibration Method for Stellar Camera[J]. Science of Surveying and Mapping, 2009, 34(2): 121-123. (in Chinese)
[9] 钟红军, 杨孟飞, 卢欣. 星敏感器标定方法研究[J]. 光学学报, 2010, 30(5): 1343-1348. ZHONG Hongjun, YANG Mengfei, LU Xin. Calibration Method of Star Tracker[J]. Atca Optica Sinica, 2010, 30(5): 1343-1348. (in Chinese)
[10] 王之卓. 摄影测量原理[M]. 北京: 测绘出版社, 1979. WANG Zhizhuo. Photogrammetric Principle[M]. Beijing: Sino Maps, 1979. (in Chinese)
[11] 冯文灏.近景摄影测量[M].武汉: 武汉大学出版社, 2002. FENG Wenhao. Close Range Photogrammetry[M]. Wuhan: Wuhan University Press, 2002. (in Chinese)
[12] 谢俊峰, 江万寿, 龚健雅.顾及星像点分布的恒星相机在轨检校[J]. 北京航空航天大学学报, 2011, 37(10): 1271-1276. XIE Junfeng, JIANG Wanshou, GONG Jianya. On-orbit Calibration of Stellar Camera Considering Distribution of Star Image Points[J]. Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(10): 1271-1276. (in Chinese)
[13] 李江操. 基于星敏感器的星图识别算法的研究[D]. 成都: 中国科学院大学(中国科学院光电技术研究所), 2018. LI Jiangcao. Research of Star Identification Algorithm Based on Star Tracker[D]. Chengdu: University of Chinese Academy of Sciences, 2018. (in Chinese)
[14] 孙利, 江洁, 李健, 等. 多视场星敏感其结构参数标定方法[J].北京航空航天大学学报, 2015, 41(8): 1532-1538. SUN Li, JIANG Jie, LI Jian, et al. Structural Parameter Calibration Method for Multiple Field of View Star Tracker[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1532-1538. (in Chinese)
[15] 刘宇, 戴东凯, 伏思华, 等. 星敏感器内参数标定误差研究[J]. 光学与光电技术, 2017, 15(6): 77-83. LIU Yu, DAI Dongkai, FU Sihua, et al. Research on the Calibration Errors of Star Tracker Intrinsic Parameters[J]. Optics & Optoelectronic Technology, 2017, 15(6): 77-83. (in Chinese)
[16] 张友民, 戴冠中, 张洪才. 卡尔曼滤波计算方法研究进展[J]. 控制理论与应用, 1995(5): 529-538. ZHANG Youmin, DAI Guanzhong, ZHANG Hongcai. The New Development of Kalman Filtering Algorithms[J]. Control Theory and Applications, 1995(5): 529-538. (in Chinese)
[17] 张洪才, 张友民, 贺志斌. 一种鲁棒自适应推广卡尔曼滤波及其在飞行状态估计中的应用[J]. 信息与控制, 1992, 21(6): 343-348. ZHANG Hongcai, ZHANG Youmin, HE Zhibin. A Robust Adaptive Extended Kalman Filter and Its Application to Flight State Estimation[J]. Information and Control, 1992, 21(6): 343-348. (in Chinese)
[18] 马平. 卡尔曼滤波算法的收敛速度[J]. 山东师大学报(自然科学版), 1997(3): 325-328. MA Ping. Convergence Rate of Kalman Filter Algorithm[J]. Journal of Shandong Normal University(Natural Science), 1997(3): 325-328. (in Chinese)
[19] 谢俊峰, 唐新明, 莫凡, 等. 资源三号国产星敏感器事后定姿方案设计与系统实现[J].武汉大学学报(信息科学版), 2017, 42(4): 434-440. XIE Junfeng, TANG Xinming, MO Fan, et al. Domestic Stellar Image Post-processing Project Design and System Implementation for ZY-3 Satellite[J]. Geomatics and Information Science of Wuhan University, 2017, 42(4): 434-440. (in Chinese)
[20] 毛燕清, 徐玉玲, 甘雅婧, 等. 资源三号卫星影像在1:1万地形图更新中应用研究[J].江西测绘, 2018(3): 29-31. MAO Yanqing, XU Yuling, GAN Yajing, et al. The Application of ZY3 Satellite Images in Updating 1:10000 Topographic Maps[J]. Jiangxi Surveying and Mapping, 2018(3): 29-31. (in Chinese)
[21] 唐新明, 谢俊峰, 张过. 测绘卫星技术总体发展和现状[J]. 航天返回与遥感, 2012, 33(3): 17-24. TANG Xinming, XIE Junfeng, ZHANG Guo. Development and Status of Mapping Satellite Technology[J]. Spacecraft Recovery & Remote Sensing, 2012, 33(3): 17-24. (in Chinese)
[22] 岳阳阳. 双CCD星敏感器标定方法研究[D]. 长沙: 国防科学技术大学, 2015. YUE Yangyang. Calibration Method of Double-CCD Star Sensor[D]. Changsha: National University of Defense Technology, 2015. (in Chinese)
[23] 孙利, 江洁, 李健, 等. 多视场星敏感器结构参数标定方法[J]. 北京航空航天大学学报, 2015, 41(8): 1532-1538. SUN Li, JIANG Jie, LI Jian, et al. Structural Parameter Calibration Method for Multiple Filed of View Star Tracker[J]. Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(8): 1532-1538. (in Chinese)
On-orbit Geometric Calibration of Star Tracker Based on EKF
LI Xiang1XIE Junfeng1,2*MO Fan2ZHU Hong2JIN Jie1
(1 School of Surveying and Geographical Science, Liaoning Technical University, Fuxin 123000, China)(2 Land Satellite Remote Sensing Application Center, MNR, Beijing 100048, China)
The geometric calibration of star tracker on orbit is one of the effective means to eliminate the systematic measurement error and improve the accuracy of attitude determination. As to the present calibration method with star-pair angular distances, theleast square method is mostly used to obtain the globally optimal static parameters to be calibrated, which does not fully characterize the small dynamic changes of internal parameters caused by the variations of outer space environment during the operation of star cameras. In order to further improve the on-orbit calibration accuracy of star tracker parameters, based on the preprocessing of the star map recognition results, this paper introduces Extended Kalman Filter (EKF) to calibrate the camera parameters corresponding to the current star map moments in real time and dynamically obtain the current optimal parameter values. Using the method proposed in the article, the ZY-3 01/02 domestic star tracker is calibrated on orbit. The test results show that the proposed method can effectively calibrate the parameter error of the current star tracker, with better accuracy, adaptability and reliability than the traditional least square method. The proposed method can be used for real-time satellite orbit calibration or ground satellite attitude post-processing, providing a technical reference for on-orbit geometry calibration of star tracker.
Extended Kalman Filter(EKF); on-orbit calibration; star tracker; high resolution earth observation
TN433
A
1009-8518(2019)03-0082-12
10.3969/j.issn.1009-8518.2019.03.011
李响,男,1996年生,2017年获辽宁工程技术大学测绘科学与技术专业学士学位,现为辽宁工程技术大学测绘科学与技术专业硕士研究生。研究方向是星敏感器标定与定姿。E-mail:li_xiang_24@163.com。
谢俊峰,男,1981生,研究员,2009年获武汉大学摄影测量与遥感专业博士学位。主要研究方向为精密定姿、卫星影像几何处理以及星载激光雷达几何检校等。E-mail:junfeng_xie@163.com。
2018-12-07
国家自然科学基金(41571440,41771360);国家青年科学基金(41301525);国家测绘地理信息局青年学术带头人基金(201607);高分专项(民用部分)科研项目(42-Y20A11-9001-17/18);“十三五”民用航天技术预先研究项目(多波束激光地形探测雷达及应用技术(D040105)可见光、红外、激光主被动复合测绘相机及应用技术(D040106))
(编辑:庞冰)

