在“联”和“通”中构建新系统获得新见解——关于《立体图形的表面积和体积总复习》同课异构带来的思考

蒋守成（特级教师）

据统计，小学数学教学时间大约有五分之一是用在整理和复习上的，相应地，教材编写的“整理与复习”也占有一定的篇幅，既有单元的整理复习，也有整册书的整理复习，教材在六年级下册还用近一半的篇幅编排小学数学知识的“整理和复习”。我们该如何定位学生的整理和复习？在我看来，复习就是对已学过的知识进行重新学习，这种重新学习并不是对已学知识的简单重复，而是进行更高层次的再学习，正如孔子所说：温故而知新，可以为师矣。通过复习，把教材中的各部分知识进行归纳整理，综合拓展，以达到巩固提高、融会贯通的目的。那整理和复习教学的核心是什么？就是要帮助学生从认识事物的本质进而认识事物之间的有机联系，让学生充分经历整理、分类、概括提升的过程，逐步完善学生已有的认知结构，促进学生形成结构化、系统化的思维方式，提升思维品质。杭州市和睦小学的胡胜平和常州市金坛区朝阳小学的谭亚鹏两位教师同课异构苏教版六年级下册《立体图形的表面积和体积总复习》一课，从整体的设计思路上明显不同，但又带着一些共性，他们都关注立体图形内在的关联，关注毕业复习课课型的特点，他们的设计从不同角度给我们以启发与思考。

一、关注联结，重视体系，促进学生编织属于自己的知识类结构

结构性是数学知识的重要特点，整理和复习教学的核心目标之一是要让学生平时所学的零碎知识系统化、条理化、清晰化，形成完善的认知结构，促使学生对知识有全面的、系统的认识与理解。

因此教学时胡老师和谭老师都注重构建系统，突出知识间的关联，让原本孤立的各个立体图形的表面积和体积“拉帮结派”，展现网络样态，有力扩张学生的认知世界，让学生站在系统的角度明晰联系、关注区别，促进学生系统化、结构化的思维方式的形成。但他们构建系统的路径不一样，胡老师基于主题在以式想形中形成结构化的思维方式，谭老师基于学生的经验在分类思考中建构。

1.在以式想形中沟通内在关联，无中生有。

学生学习过的知识有些是“碎片”化的，有些是围绕某一主题相互联系起来形成一定的知识单元存在。数学家华罗庚说，“找另一条线索把旧的东西重新贯穿起来，这也是一种有利的温习方法”。胡老师通过立体图形的体积和表面积公式为线索来梳理、沟通内在的联结，激发学生学习的主观愿望，将碎片纳入到主题结构，发展学生的思维能力，形成新的结构体系，其教学通过三个流程来创造了学生主动思考的事件。

（1）以式想形，独立思考。看到这两个公式：V=Sh S=S侧+S底×2，你想到了可以求哪些图形的体积和表面积？请你写在练习纸上。

（2）聚焦体积，分享思考。通过资源呈现，信息综合后学生形成一致观点，不光“圆柱、长方体、正方体”的体积可以用“V=Sh 的方法来求，只要是上下底面大小相等的直柱体都可以用这个公式求体积。

（3）聚焦表面积，形成新系统。教师出示学生作品，这三个立体图形虽然形状不同，但相互之间有着密切的联系，都是直柱体，所以它们的体积和表面积都可以用相同的方法来计算！

“以式想形”将原本“形”不相同的立体图形联系到了一起，从整体上建立知识间的纵横联系和层次结构， 构建起具有生长活力的认知结构和知识体系。这样的复习方式打破了我们一贯的图形分类，联系和区别这样物以类聚的思考模型，给学生们找到“以法类聚，无中生有”这样另一种思考模型，丰富了学生自我建构知识结构的路径。

2.在分类思考中构建知识体系，触类旁通。

认知结构的优化，主体是学生自己，谭老师为学生提供了“哪些立体图形能和圆柱归为一类？”作为自主梳理知识的线索，请学生在研究单上写一写分类的理由，教师呈现学生的现实资源，通过如下四次学生资源交流，让学生自主思辨，分类完善。

交流一：圆柱、圆锥、球为一类，因为它们都可以由一个平面图形通过旋转得到。

交流二：图形运动除了旋转还有平移。长方体、正方体、圆柱都可以由一个平面图形通过平移得到。所以长方体、正方体、圆柱这三个图形为一类。

交流三：长方体、正方体可以和圆柱归为一类，因为它们的体积都可以用底面积乘高来计算，它们的表面积和侧面积的计算方法也是一样的。

交流四：追问，长方体、正方体、圆柱归为一类的，那除了计算方法和平移外，这三个图形还有什么共同特征呢？揭示像这些直直的，上下两个面完全相同，而且上下粗细完全一样的立体图形，也叫做直柱体。

谭老师通过四次互动交流，帮助学生进行整体类化，并以旋转、平移、计算、特征等方式再现和强化了立体图形的内涵，很好地完成了知识横向和纵向结构化，发现和理解五种立体图形的内在联系。学生在分类的过程中，不断地让知识在大脑中重组、排列、整合，逐渐形成网络体系，也许最初看是杂乱无章的陈列，但在分类方法的帮助下，标准不同，图形呈现出的分类情况也多样化。图形间那些千丝万缕的联系逐渐清晰，形成立体图形表面积和体积内在的关联系统。

二、凸显融通，利用结构，帮助学生揭示知识内在联系

郑毓信教授提出：基础知识贵在求联，基本技能贵在求通。“整理和复习”的核心目标之二是要让学生在自我思考的基础上，揭示知识之间的内在联系，同时知识与知识相互关联过程中衍生出的新知识，能够触类旁通学数学，融会贯通用结构。这就需要我们对教材中割裂的、相互封闭的知识进行比较、融通、整合，利用内在结构获得新收获。

1.利用关联，在解决问题中贯通方法。

胡老师设计了两个连续性的情境化问题，让学生在解决问题的过程中能够利用立体图形内在的关联，化繁为简，贯通方法。“哪个积木的涂色面积更大？”呈现的问题教师进行了有意的设计，而大部分学生还是选择了直接计算（如下图），这是情理之中的。因为高相等比较容易观察，但是底面周长相等却不是那么容易可以发现的。所以大多数学生还是愿意选择直接计算。

我也欣喜地发现有学生关注到了底面周长（如下图）。虽然没写完，却已经有了这方面的意识。通过这份学生的作品引发全班学生的思考：他想表达什么意思？引导学生发现，当底面周长相等、高也相等时，要比较表面积的大小，我们只需要比较底面积的大小即可。胡老师让学生发现这两个立体图形的表面积大小不但可以用以前的公式直接计算，还可以用S=Ch+S底×2 来比较。

“哪个积木的体积更大？”在比较体积时，有了前面比较表面积的经验，我在课堂发现有将近一半的学生在比较时会有方法上的选择。

上图中，学生先选择了三个等高的直柱体进行比较，通过底面积的大小比较出正方体的体积最大，然后算出圆锥的体积，最后进行两者的比较。这是大多数学生选择的方法，这也和胡老师的预设相符：有的可以直接比，有的必须要经过算一算才能得出结果。

也有的学生先选择了等底的圆柱和圆锥进行比较，判断出圆锥的体积大。有的学生利用了“方中圆”，快速地比较出了正方体和圆柱的体积大小。最让人意外的是，还有的学生不仅观察到图形的特征，还观察到了数据的特征（如下图），认为不需要完全计算完圆锥的体积，只需要在代入数据后就能发现，四个算式（或四个图形）都有一个共同的数据“4”，只需要比较“16＞5π＞15＞4π”即可，选择了更为灵活的方法比较出了四个图形的体积大小。

两个问题的解决，给了学生思维能力提升的一次好机会，他们的思维方式不再受到限制，思考的角度更多元，解决问题策略更多样，并能选择合理的方法进行计算。学生在应用数学知识、解决实际问题的过程中，真正做到了触类旁通。

2.用好结构，在系统思考中触类旁通。

谭老师在两个板块中安排了两个教材中没有触及的问题，让学生在已有认知结构基础上再建构的内容，触类旁通学数学。

“求三棱柱的表面积、体积和圆柱的方法一样吗？”谭老师在学生形成类结构的基础上让学生自我探究，建构了直柱体的方法结构，最后通过微视频再现的方式形成完整的研究过程。

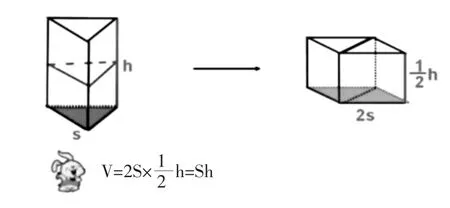
把上面左图中的三棱柱在高一半处切开，拼成一个近似的长方体，此时这个近似长方体的底面积是2S，高是所以三棱柱的体积也可以用底面积乘高来计算。三棱柱的侧面展开也是一个长方形，底面是两个一样的三角形，侧面积公式也是一致的。然后再做进一步的思考，发现求三棱柱等所有直柱体的体积和表面积的方法是一致的。

“圆柱的体积还可以用侧面积的一半乘半径。”谭老师在学生掌握了直柱体体积一般方法的基础上，设计了“草莓大棚内的空间有多大”的现实问题情境，在解决问题的过程中丰富解决问题的方法，打通了圆柱和长方体内在的关联。

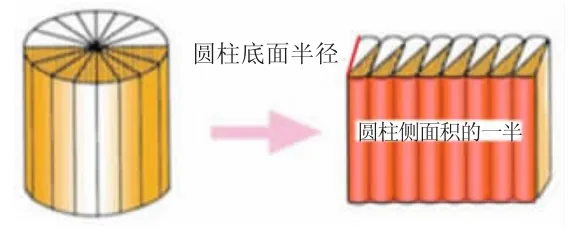
谭老师引导学生发现：如果将长方体的前面做底面，长方体的底面相当于圆柱侧面积的一半，长方体的高相当于圆柱的半径。长方体的体积=底面积×高，那圆柱的体积就等于侧面积的一半×半径。公式变了，但其求体积方法的本质没有变。

“如何求三棱柱的表面积和体积”和“圆柱的体积还可以怎么求”这两个问题“触”及“圆柱”，“通”至“长方体、正方体”。将原本在每节课里获得的“散装”的知识与方法，在形成结构的背景下进行重新组织和构建，将原来彼此分割开来的方法联结成新的统一的整体，在此过程中获得新知识，产生新见解。

两位教师的总复习课值得我们欣赏和分享的是他们都通过“联”和“通”将建构认知结构放在首要位置，因为认知结构越稳固，越有利于吸纳新的知识；他们精心安排学生学习活动，学生学会触类旁通学数学、融会贯通用结构，新系统中学生获得新知识、产生新见解，提升了学习力。

一节课不可能集结所有的精华，但不同的思考就会有不同的切入点和不同的课堂教学架构，从重构的角度来思考，我们也可以用思维导图的方式从学生自我整理开始，在过程中贯通面积和体积的统一方法，由此拓展到直柱体和圆柱的新方法；也可以用主题研究的方式进行，以一张白纸为主题，通过折、卷、转，变与不变等方式将立体图形的表面积和体积等问题贯通起来；当然也可以由现实的具有挑战性的问题解决开始，在解决问题的过程中聚焦方法、形成系统。

不同的架构只是我们课堂开始的触点不一样，我们的目标是一样的， 构建知识体系，揭示内在联系，不断促进学生形成结构化、系统化的思维方式。对于整理复习课我们还可以做更系统的思考，“如何上好单元复习课”“如何上好期末复习课”“如何上好毕业复习课”，期待更多的人一起来实践、来探讨，敢于在不同阶段的复习课上突破积习，推陈出新，对于下一节复习课，我们就有了努力的新方向。