某弹鼓构件参数化分析与结构优化

樊永锋，张海洋，刘明敏，吴宝双，徐志远，陈 雷

(中国船舶重工集团公司第七一三研究所， 郑州 450015)

为了准确对某弹鼓进行参数化分析与结构优化，采用虚拟样机软件ADAMS/View对其构件进行参数化建模和仿真分析，进行优化设计。在建立参数化模型时，根据需求分析确定相关的关键参数，并将这些关键参数设置为设计变量，在参数化分析时，只需要改变这些变量值的大小，虚拟样机模型就能够自动更新，以便观察不同参数值下样机性能变化[1]。

进行参数化建模时，ADAMS/View提供了4种参数化的方法：参数化点坐标、设计变量、参数化运动方式和参数化表达式[2]。洪吉超等[3]通过参数化点坐标方法对滚动轴承进行参数化建模与动力学仿真，优化高速轴承的动力学特性。郭小宁[4]利用参数化点坐标方法，建立挖掘机工作装置机构系统模型，实现挖掘机虚拟样机工作装置的尺寸参数化驱动和运动约束。梁爽等[5]提出1种以三维参数化仿真为核心，进行压气机静叶联调机构方案设计的方法。

胡正勇等[6]利用ADAMS软件进行二次开发功能，建立某款塑壳断路器机构参数化设计模型，实现断路器部件的参数化和约束自适应调整。本文利用设计变量参数化弹鼓模型中构件——进弹导引为例，研究导引参数化分析及结构优化，可以提高弹鼓机构分析设计效率。

1 进弹导引工作原理

进弹导引是弹丸由进弹口进入弹鼓的连接机构，主要由两侧导引肋板组成，其实体模型如图1所示。

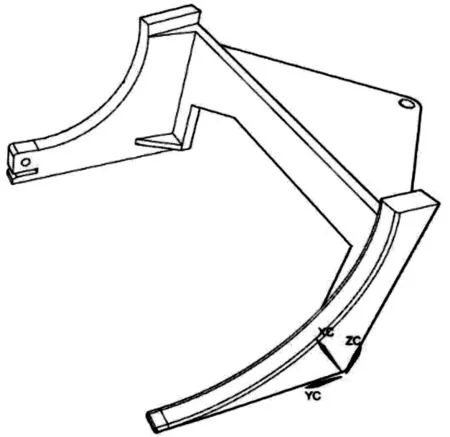
图1 进弹导引三维实体模型

在供弹的过程中，弹丸在进弹导引两侧肋板上运动，有约束弹丸运动和调整弹丸姿态的作用，如图2所示。

图2 弹丸在进弹导引肋板上运动示意图

2 进弹导引参数化建模

在ADAMS/View中，可以通过设计变量定义自变量参数，方便地改变虚拟样机的任何对象，当设计变量参数改变时，所有同设计变量相关联的对象也都随之改变，通过参数化分析，令设计变量在一定范围内变化，从而自动进行一系列参数化分析。

进弹导引两侧肋板对供弹动作影响较大，故采用设计变量DV_1、DV_2来控制两侧肋板半径大小(如图3所示)，对与设计变量相关联的进弹导引属性进行更新，分析对弹鼓供弹性能的影响参数，找到合理尺寸数值。进弹导引两侧肋板原始数值为R1=62.50 mm、R2=48.00 mm，则设计变量DV_1取值范围为(60.50，64.50)mm，DV_2取值范围为(46.00，50.00)mm。

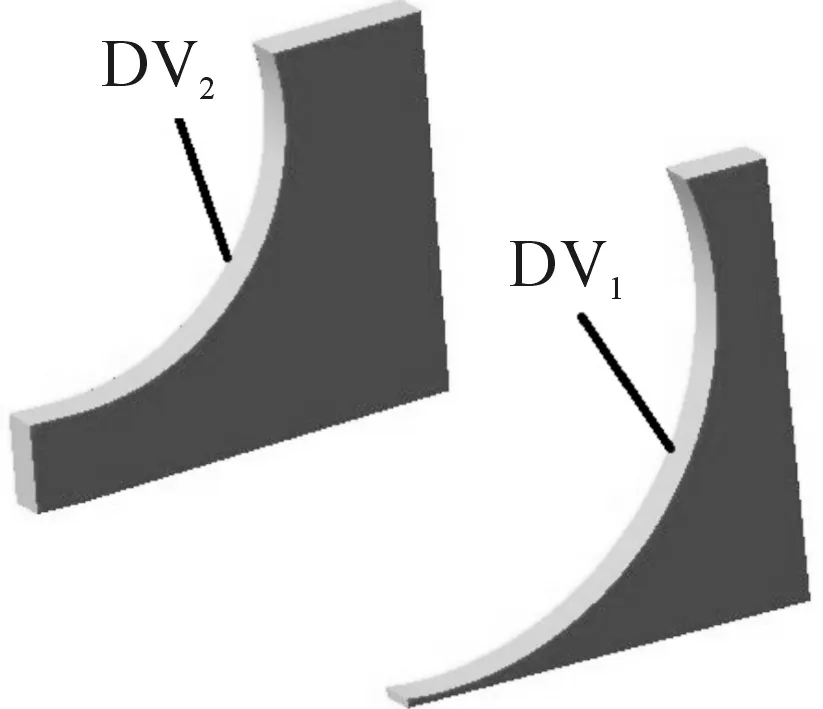
图3 进弹导引肋板参数化模型

3 参数化仿真分析

3.1 建立目标函数

目标函数是用数学方程来表示模型质量、效率、成本、稳定性等。使用精确数学模型的时候，最优的函数值对应着最佳的设计[7]。目标函数是参数化分析判断的依据，可以根据目标函数来确定相关尺寸[8]。在对进弹导引参数化设计过程中，选择与弹丸最大峰值接触力中的最小值为目标函数，如图4所示。

图4 建立目标函数

3.2 仿真分析

对进弹导引进行参数化仿真过程中，在设计变量范围内依次选取5组数据，进行参数化分析，得到设计变量DV_1对应接触力随时间变化曲线如图5所示，设计变量DV_1报告如图6所示。

图5 设计变量DV_1对应接触力随时间变化曲线

图6 设计变量DV_1报告

根据设计变量DV_1报告，在DV_1的5次取值过程中，62.50 mm所对应的最大峰值接触力在5组数据中为最小，其峰值接触力为315.79 N。

同理可以对设计变量DV_2进行参数化仿真，得到设计变量DV_2对应接触力随时间变化曲线如图7所示，设计变量DV_2报告如图8所示。

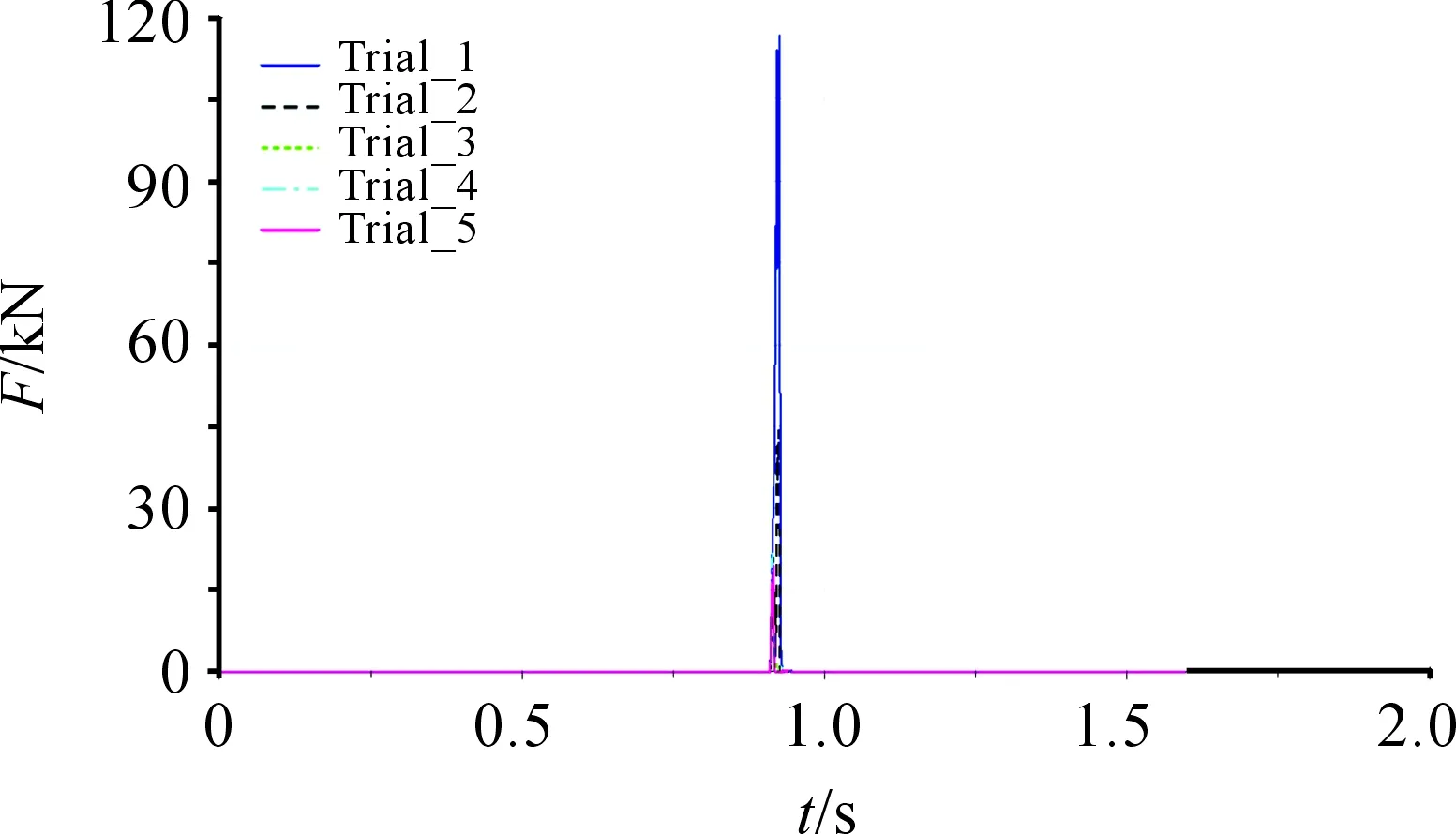
图7 设计变量DV_2对应接触力随时间变化曲线

图8 设计变量DV_2报告

根据设计变量DV_2报告，在DV_2的5次取值过程中，47.00 mm所对应的最大峰值接触力为18 402 N，比原始数据48.00 mm所对应的最大峰值接触力21 650 N小，是合理取值。

4 Insight试验优化设计

Insight是以设计复杂的试验来评价机械系统的性能[9]，提供一系列的统计工具以帮助更好的分析结果，利用Insight，进行单目标优化或者多目标优化计算。

在Insight设计因素中，设计变量DV_1标准取值为62.50 mm，公差为(0.05)mm，默认数据变化类型为连续。在设计范围内进行变化，设置DV_1服从正态分布，得到设计变量DV_1正态分布如图9所示。

图9 设计变量DV_1正态分布

根据设计变量DV_2参数化结果， DV_2标准取值为47.00 mm，公差为(0.05)mm，默认数据变化类型为连续。在设计范围内进行变化，设置DV_2服从正态分布，得到设计变量DV_2正态分布如图10所示。

图10 设计变量DV_2正态分布

Insight中，通过改变设计变量值的大小，利用相对灵敏度分析结果，研究哪些因素的影响比较大，并且根据这些因素之间的关系获得最佳目标[10]。

创建进弹导引的响应为最大的峰值接触力为最小，利用回归分析方法，研究因素对应的响应关系，可以确定设计变量DV_1、DV_2对最大的峰值接触力的影响即参数灵敏度，如图11所示。设计变量DV_1、 DV_2对弹鼓供弹系统动态性能的影响为0.42%和0.32%。

图11 相对灵敏度结果

根据ADAMS参数化计算结果，对优化后的尺寸进行仿真分析，计算出在进弹导引尺寸优化基础上的峰值接触力，如表1所示。

表1 进弹导引优化前后对比

5 结论

1) 根据将进弹导引建立参数化模型，在参数化分析后得到进弹导引两个肋板半径为R1=62.50 mm、R2=47.00 mm，峰值接触力相对减小18.13%。

2) 根据Insight优化设计，利用设计变量DV_1、DV_2正态分布计算出参数灵敏度为0.42%和0.32%，证明了进弹导引优化的可行性，取得满意的效果。

3) 本文采用理想的刚体模型，没有考虑构件的变形，相对于实际情况有一定误差。当设计基本定型时再采用柔性模型进行更精确的仿真验证。