适配器新型基体材料热-粘-超弹本构模型研究
张英琦,乐贵高,马大为,冯国铜
(1.南京理工大学 机械工程学院, 南京 210094;2.苏州工业职业技术学院 精密制造工程系, 江苏 苏州 215104)
军用适配器是导弹发射系统中的关键部件之一,国外常称为侧向减振支持系统[1-2]。配置在发射筒与导弹之间的弹性支承系统,在导弹贮存和运输过程中起缓冲减振作用,在导弹发射过程中起支承、导向与减振作用。
自20世纪40年代以来,导弹发射系统中采用的适配器基体材料绝大多数为橡胶材料,而相较于橡胶材料,聚氨酯弹性材料具有定伸强度大、扯断伸长率大、扯断变形率小、耐磨、耐老化、耐撕裂、与金属之间的粘结性能良好等优势[3-4],且其各项物理力学性能指标均可通过对原材料的选择和配方按需调整。
适配器在导弹贮存、运输和发射过程中,受导弹惯性和冲击作用,基体材料发生大应变率跨度(0.01~3 500 s-1)的压缩变形。发动机喷出的高温高压燃气射流直接作用在适配器上,适配器基体材料力学特性受温度的影响不可忽略。
本文选用新型PU2531聚氨酯弹性体作为适配器的基体材料,对其材料力学性能的研究是适配器精确数值建模的基础。首先,通过准静态和动态压缩实验获取不同温度不同应变率下材料的压缩应力-应变曲线;其次,建立了含温度效应项的粘-超弹本构模型,根据实验结果拟合了本构模型中的相关参数;最后,编写了用户子程序VUMAT,将单轴压缩实验与数值解进行对比验证。
1 不同温度不同应变率下的压缩实验
针对新型聚氨酯弹性体材料,开展不同温度不同应变率下的单轴压缩实验,获取材料应力-应变曲线,为热-粘-超弹本构模型参数拟合提供依据。
利用准静态单轴压缩实验装置和分离式霍普金森压缩实验装置(SHPB),对新型适配器基体材料A型压永试件[5]如图1所示,进行了温度为273 K,应变率为0.01 s-1时的准静态单轴压缩实验,以及温度为253 K、273 K、291 K、313 K、338 K、363 K,应变率为800 s-1、1 600 s-1、2 000 s-1、2 500 s-1、3 500 s-1、4 600 s-1的动态单轴压缩实验。

图1 聚氨酯试件
图2为0 μs和40μs时刻PU2531试件变形照片。通过实验数据获得了PU2531聚氨酯弹性体试件压缩应力-应变响应特性,如图3和图4所示。

图2 0 μs和40 μs时刻PU2531试件变形照片

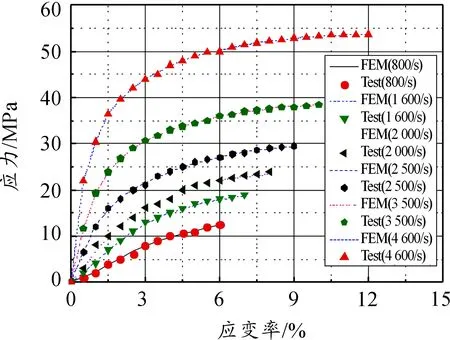
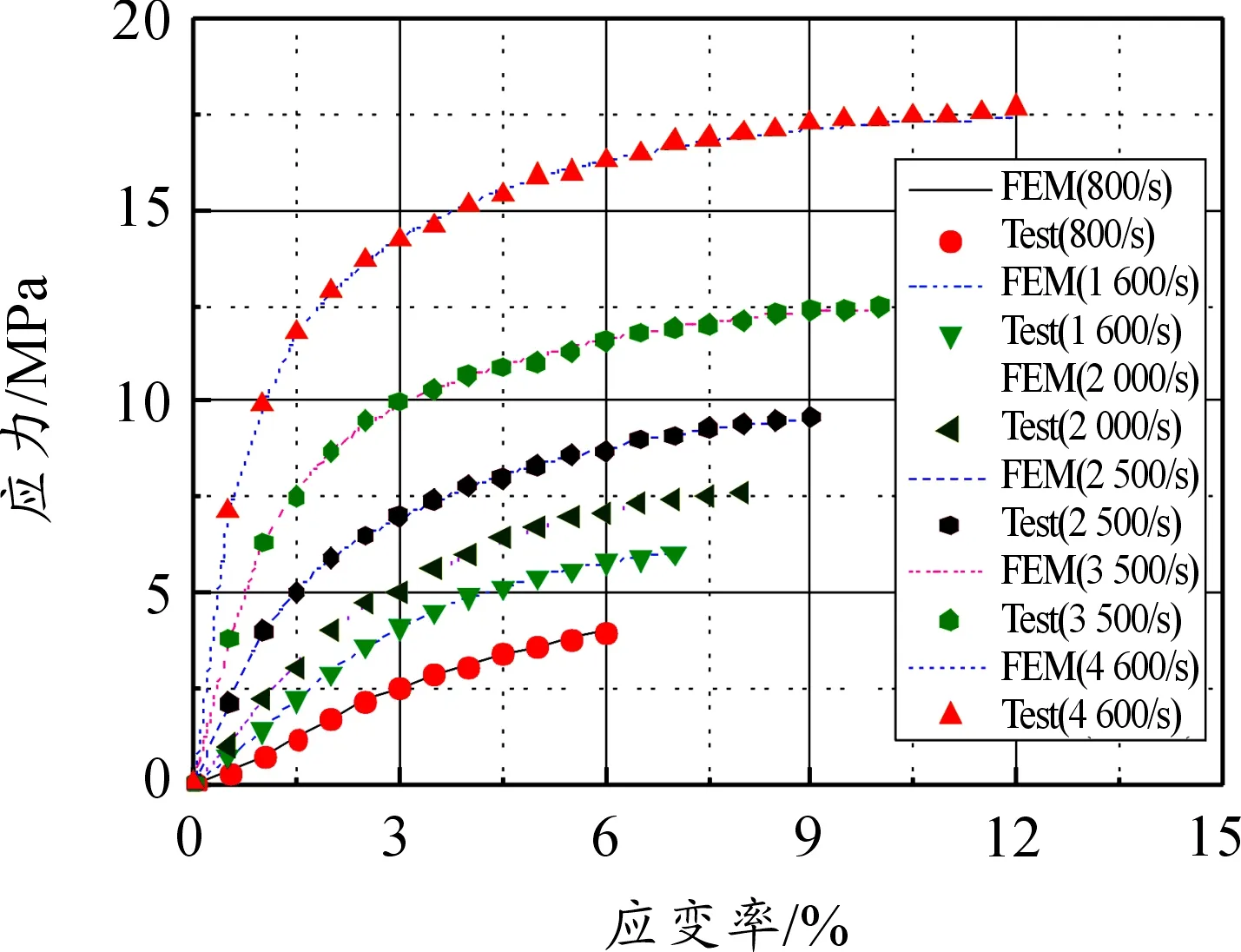
图3 253 K下不同应变率压缩应力-应变实验值
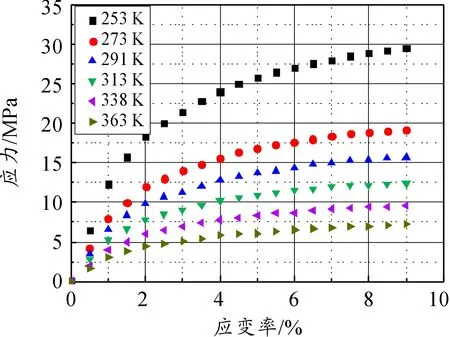
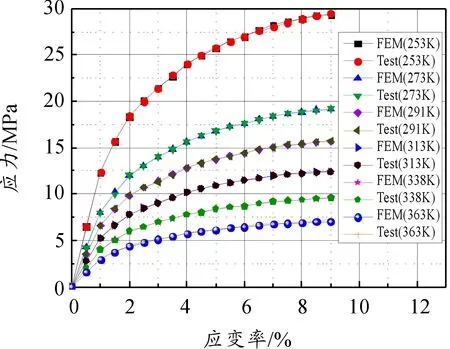
图4 2 500 s-1下不同温度压缩应力-应变实验值
从应力-应变曲线可以看出,随着应变的增大、应变率的增大或者温度的降低,聚氨酯弹性体单轴压缩的应力增大,聚氨酯弹性体材料表现出一定的率相关性和温度相关性。
2 热-粘-超弹本构模型
根据新型聚氨酯弹性体材料不同温度不同应变率下的力学特性,提出一种应变硬化、应变率强化、温度软化效应的非线性热-粘-超弹本构模型。
2.1 超弹性本构模型
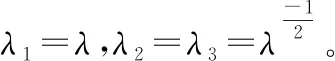
(1)

W=W(I1,I2,I3)
(2)
(3)
对于不可压缩聚氨酯弹性体材料,根据能量守恒定律,各向同性不可压缩聚氨酯弹性体材料的本构方程为:
(4)
式中,σe|Tref为参考温度Tref时Cauchy应力张量,Pe为静水压力,I为单位张量。
在聚氨酯弹性体应变范围内,选用二阶多项式本构模型来描述该类聚氨酯弹性体的本构关系,而聚氨酯弹性体为不可压缩材料,故应变能函数为:
(5)
根据Rivlin和Saunders[7]对超弹性材料的系统实验研究发现,对于二阶多项式本构模型,为了确保Cij在单轴实验、双轴实验和剪切实验中具有良好的一致性,应采用如下形式的应变能密度函数:
We=C1(I1-3)+C2(I2-3)+C3(I2-3)2
(6)
2(C1+ 2C3)λ-1-2(C2-6C3)λ-2-4C3λ-4
(7)
在单轴压缩加载方向上的拉伸比和工程应变的关系为λ=ε(ε为工程应变)。结合聚氨酯弹性体材料准静态单轴压缩实验数据,利用最小二乘法拟合确定超弹性本构方程中的参数。
2.2 广义粘弹性本构模型
粘弹性材料最大的特点就是其力学性能受之前变形的影响,其应力依赖于应变和应变率历史。结合Gamonpilas[8]提出的非线性粘弹性本构模型,将应变ε和时间t对应力的影响效应进行解耦,则非线性粘-超弹本构模型可假设为:
σ(ε,t)=σ0(ε)·g(t)
(8)
式中,σ为应力张量,ε为应变张量,g(t)为无量纲函数。
无量纲函数g(t)通常可用Prony级数表示:
(9)
式中,θi为松弛时间,N为松弛时间的组数,g∞和gi为无量纲参数表征超弹性和粘弹性的权重。
低应变率下(t=∞),可得应力的平衡响应为σ(ε,∞)=σe=g∞·σ0(ε),而高应变率下(t=0),σ(ε,0)=σins=σ0(ε),σ0(ε)为应力的瞬态响应。则应力的平衡响应和瞬态响应比值为g∞,为了不失一般性,令g∞和gi随应变而改变,即g∞=g∞(ε),gi=gi(ε),则
(10)
积分形式的本构方程能直接反映粘弹性材料的记忆特性,结合Leaderman卷积积分和
聚氨酯弹性体非线性粘弹性本构方程为:
(11)
将本构方程分解为超弹性应力部分和粘弹性应力部分,三维全量格式粘-超弹性本构模型为:
σ(ε,t)=σe+σv=g∞(ε)·σ0(ε)+
(12)

(13)

本文假设加载前材料的应力状态不影响加载后的应力状态,即时间积分下限为零,取N=1,用来描述高应变率下的情况,而不考虑低应变率范围内的应变率敏感性。联立式(12)和式(13)可得
(14)
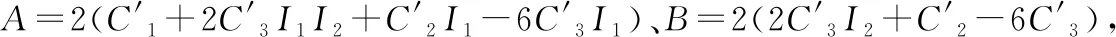
(15)
(16)
(17)
(18)
2.3 基于J-C温度效应项的热-粘-超弹本构模型
聚氨酯弹性体适配器在导弹发射环境和发射过程中,服役温度广,温度T对材料力学性能的影响不可忽视。而J-C本构模型应用范围较广,模型中的热效应项能适用于金属、土壤、混凝土、橡胶等各种材料。Johnson-Cook模型采用连乘的形式将应变强化效应、应变率敏感性和温度软化效应综合处理,具有形式简单各项物理意义明确的优点。根据上述超弹性本构模型、粘弹性本构模型及Johnson-Cook模型的温度效应项,本文提出一种应变硬化、应变率强化、温度软化效应的非线性热-粘-超弹本构模型为:
σ|T= (σe|Tref+σv|Tref)(1-θn)
(19)
(20)
式中,σ|T为T温度下材料的真实应力,n为无量纲系数,T为工作温度,Tf为材料粘流态温度,Tg为材料玻璃化转变温度,温度关系满足Tg 通过式(19),结合不同温度下动态单轴压缩实验数据,拟合出非线性热-粘-超弹本构模型中8个未知参数。 本文在应变和时间效应解耦基础上,建立了参数少且物理意义明确的非线性热-粘-超弹本构模型,该本构模型可预测该类聚氨酯弹性体在不同温度不同应变率下力学响应特性,能够较为准确地描述导弹发射过程中,聚氨酯弹性体适配器在高温燃气流冲击和高应变率下的变形特性。 表1 热-粘-超弹本构模型参数拟合值 ABAQUS现有材料库中未包含非线性热-粘-超弹本构模型的相应模块,但其本身提供了各种丰富的用户子程序接口来定义材料属性,使ABAQUS在计算时能调用材料库中没有定义的材料模型。为了验证上节中建立的热-粘-超弹性本构模型的有效性,利用建立的聚氨酯弹性体热-粘-超弹本构模型的VUMAT子程序,对霍普金森压杆实验的压缩过程进行模拟。如图5聚氨酯弹性体材料HSPB数值模型图所示,入射杆和透射杆的实际长度远大于聚氨酯弹性体试件厚度,为使图片能够清晰显示数值模型网格划分情况,故将图中入射杆和透射杆沿虚线做断开显示。为了简化数值模型计算规模,利用数值模型的便捷性能,将实际的霍普金森压杆装置进行一定的简化,将管状子弹与入射杆进行绑定约束,忽略一些附加小部件及小细节处理,降低网格划分的难度且减少了计算量。 图5 PU2531聚氨酯弹性体材料HSPB数值模型图 在管状子弹和透射杆上施加位移边界条件,利用Abaqus/Standard算法来模拟聚氨酯弹性体准静态单轴压缩实验。将霍普金森拉杆实验数值模型中显式动态算法修改为隐式静态算法,即可模拟聚氨酯弹性体试件的准静态单轴压缩实验,聚氨酯弹性体材料273 K温度下的准静态工程应力-工程应变数值与实验曲线如图6所示。 图6 273 K准静态下应力-应变数值结果与实验结果 采用Abaqus/Explicit进行霍普金森压杆实验模拟计算,利用对管状子弹施加瞬态速度的方式来实现真实情况的冲击加载,通过不同的瞬态速度来模拟不同应变率下的加载情况。在霍普金森压杆数值模型的入射杆和透射杆上按照试验中应变片粘贴位置选取单元,获得入射波、透射波和反射波的应变波形,根据不同温度不同应变率下的应变波形,可计算出不同温度不同应变率下聚氨酯弹性体试件的应力-应变数值解。 图7和图8分别为温度253 K和338 K时不同应变率下聚氨酯弹性体试件压缩应力-应变数值与实验结果。 图7 253 K应力-应变曲线 图8 338 K应力-应变曲线 图9和图10分别为应变率为1 600 s-1和2 500 s-1时不同温度下聚氨酯弹性体试件压缩应力-应变数值与实验结果对比。 图9 1 600 ss-1应力-应变曲线 图10 2 500 s-1应力-应变曲线对比 对比不同温度及应变率下的模型计算结果与实验结果,在工程应变小于10%范围内,工程应力数值解与实验值吻合程度较高。说明在聚氨酯弹性体材料应变小于10%的范围内,文中建立的热-粘-超弹本构模型能够有效地预测单轴加载方向的力学响应特性,验证了该本构模型的有效性。 提出了一种应变硬化、应变率强化、温度软化效应的非线性热-粘-超弹本构模型,利用Abaqus开发了该本构模型用户子程序,通过对比不同温度不同应变率霍普金森压杆实验数值模型结果与实验结果,验证了应变在10%以内的本构模型及用户子程序的有效性。3 本构模型参数拟合及有效性验证
3.1 本构模型参数拟合
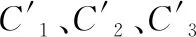
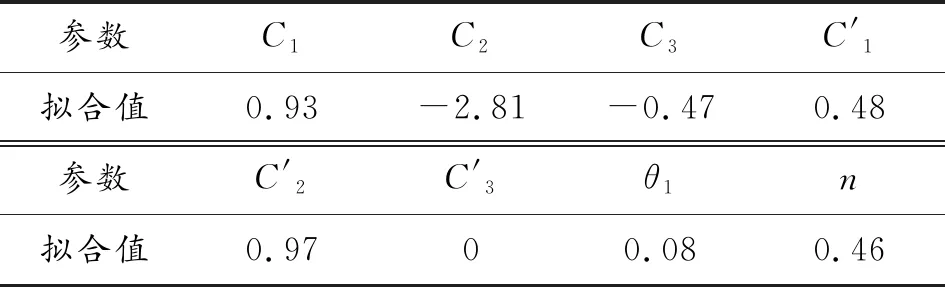
3.2 本构模型有效性验证



4 结论

