偏导射流式压力伺服阀双模糊控制

茹亚东,王 华,王 莹

(1.新乡职业技术学院 数控技术系,河南 新乡 453000; 2.山东理工大学 机械工程学院,山东 淄博 255022)

偏导射流伺服阀涉及机械、液压、电子和传感器等理论知识,具有驱动大直径阀芯的滑阀、使用寿命长、输出功率大等优点,广泛应用于汽车、矿山、航空及海洋等许多领域[1].我国对偏导射流伺服阀研究起步时间较晚,可查阅的理论资料相对较少,与国外相比,差距较大.因此,研究偏导式射流阀对于促进国家工业的发展具有重要意义.

为了提高偏导式射流阀驱动控制精度,国内外研究者对偏导式射流阀进行了广泛研究.例如:文献[2-3]研究了偏导式射流伺服阀射流模型,根据动量守恒定律解决高速喷射速度变化问题,设计出简化的二次射流模型,通过实验数据验证射流盘接收口压力变化特性,从而降低了伺服阀驱动压力误差.文献[4-5]研究了偏导射流阀建模方法和动态特性,建立射流阀数学模型,提出前置级液压动力计算简化方法,通过仿真验证数学模型的有效性,为偏导射流伺服阀的优化设计提供理论基础.文献[6-7]研究了射流管伺服阀冲蚀模拟方法,分析了射流管伺服阀工作原理,推导出伺服阀冲蚀磨损率方程式,建立其三维仿真模型,通过实验和仿真结果进行对比,得出了伺服阀工作的冲蚀磨损数据.以往研究的射流伺服阀控制在受到负载力增大时,其误差波动幅度较大.对此,本文采用自适应调整的双模糊控制策略,以负载反馈和误差反馈作为两个模糊控制器的输入,通过Matlab软件对输出误差进行仿真验证,并且与PID控制器进行对比,为提高偏导射流式压力伺服阀控制精度提供理论依据.

1 压力伺服阀

本文采用偏导射流压力伺服阀为车辆刹车系统,其结构如图1所示.

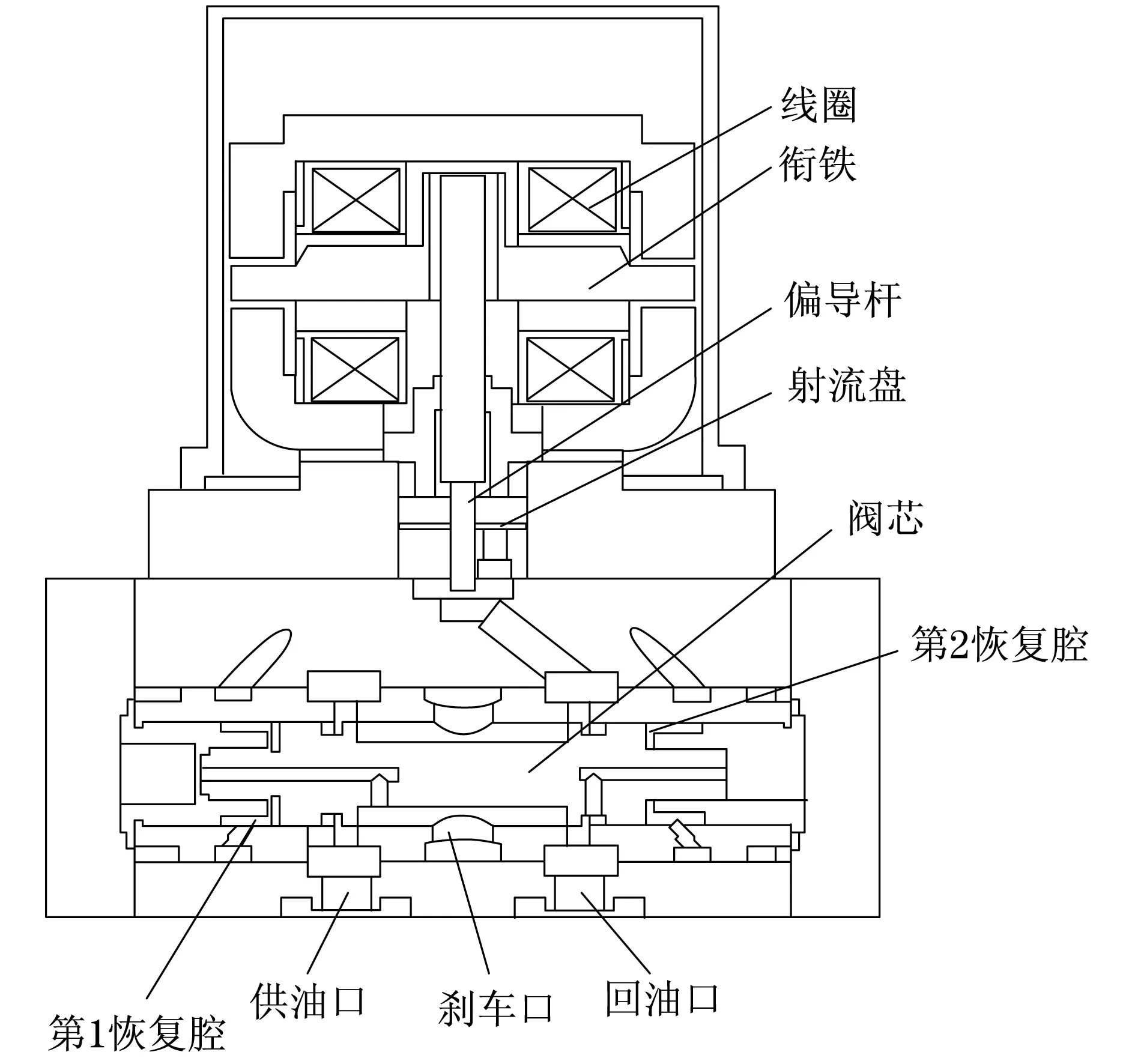
图1 偏导射流压力伺服阀Fig.1 Bias jet pressure servo valve

以车辆刹车驱动为例,介绍偏导射流压力伺服阀的具体工作原理如下:

(1) 线圈通电后使衔铁发生旋转,进而带动偏导杆旋转,使射流盘接收口面积发生变化,导致阀芯控制腔的恢复压力发生偏差,推动阀芯移动,压力油通过供油口接通刹车口,输出刹车力,当反馈力等同阀芯推动力时,阀芯停止运动,输出恒定的刹车力,即为刹车状态.

(2) 线圈断电后,衔铁受到磁场作用处于中位状态,偏导杆伴随衔铁作用也处于中位状态,射流盘的喷口对向偏导杆的中位,使射流盘接收口接通第1恢复腔和第2恢复腔,供油口、射流盘、阀芯、第1恢复腔和第2恢复腔压力保持相同,使阀芯维持在初始位置,刹车口接通回油口,无刹车力,即为非刹车状态.

力矩马达的扭矩方程式[8]为

(1)

式中:U,Ub为电力直流网络电压;R为电磁绕组的电阻;I为电力网络电流函数;L为电磁绕组的电感;Kn,Ku,Ko为液压分配器反电动势系数.

喷射管的运动方程式[8]为

(2)

式中:J为喷射管的惯性矩;Km1,Km2为电力位置增益系数;b为摩擦力系数，Ca为活塞弹簧的硬度.

流量方程式[8]为

(3)

式中:A为活塞有效面积;W0为气缸内液压流体体积;E为液压流体的弹性模量;Pd为液压流体在缸体之间的压力;μQ为流体在管道中流动系数;ξP为通过管道流体的压力系数;z为管子的位移.

活塞的运动方程式[8]为

(4)

式中:M为质量;b为摩擦力系数;R为活塞上的静态负载.

2 双模糊控制器设计

2.1 PID控制器

PID控制器由控制器和控制对象构成,如图2所示.通过输出信号反馈来调整比例、积分和微分系数,使控制对象输出误差符合设计要求.

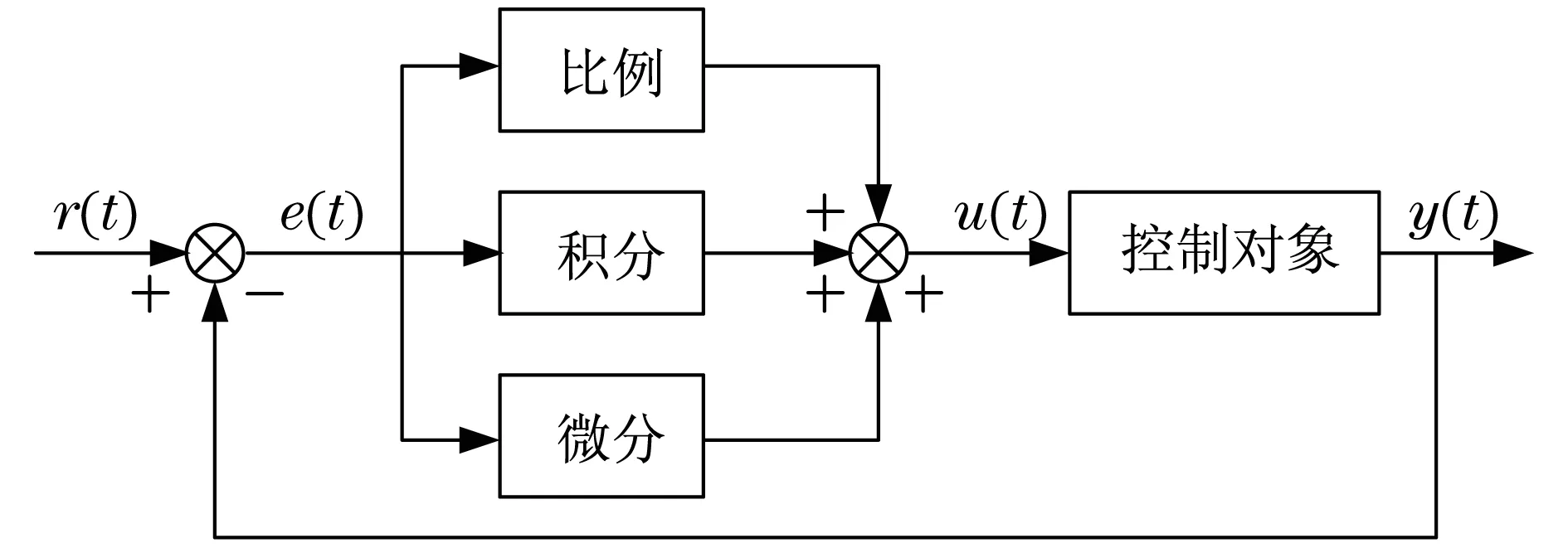
图2 PID控制器控制过程Fig.2 PID controller control process

采用PID控制器,其控制方程式[9]为

(5)

式中:kp为比例调节系数;ki为积分调节系数;kd为微分调节系数.

2.2 双模糊控制

在模糊PID控制器基础上,根据负载反馈,建立新的模糊控制器,调节模糊PID控制器的输出论域,实现负载特性的补偿.论域收缩和扩张过程如图3所示.

图3 论域变化过程Fig.3 Process of domain change

假设PID控制器比例调节系数增量Δkp初始论域为[-Ep,Ep],论域的变化因子为αp,则经过变化后Δkp的论域为[-αpEp,αpEp].同理,积分调节系数、微分调节系数经过变化后Δki和Δkd的论域分别为[-αiEi,αiEi]和[-αdEd,αdEd].

由于负载弹簧刚度变化会影响输入负载力的大小,因此,对负载力进行归一化处理[10].负载力经过归一化处理后F的论域为[0,1].为避免换向过程中产生冲击或跟踪误差较大,隶属度函数论域采用两段密集和中间稀疏,如图4所示.NB为负大，NM为负中，NS为负小，Z为零，PS为正小，PM为正中，PB为正大.

同理,负载力变化量ΔF采用归一化处理后的论域为[-1,1],采用模糊化对隶属度函数进行处理,如图5所示.

图4 隶属度函数(输入负载力)Fig.4 Membership function (input load force)

图5 隶属度函数(输入负载力变化量)Fig.5 Membership function (variation of input

模糊PID控制器的论域变化因子是通过负载力F和负载力的变化量ΔF进行求解.假设P参数中变化因子为αp,则论域为[αp,min,αp,max].采用三角函数作为αp,αi和αd的隶属度函数.

根据隶属度函数和模糊规则表,可以推导出论域变化因子αp,αi和αd.以变化因子αp为例,模糊规则如表1所示.

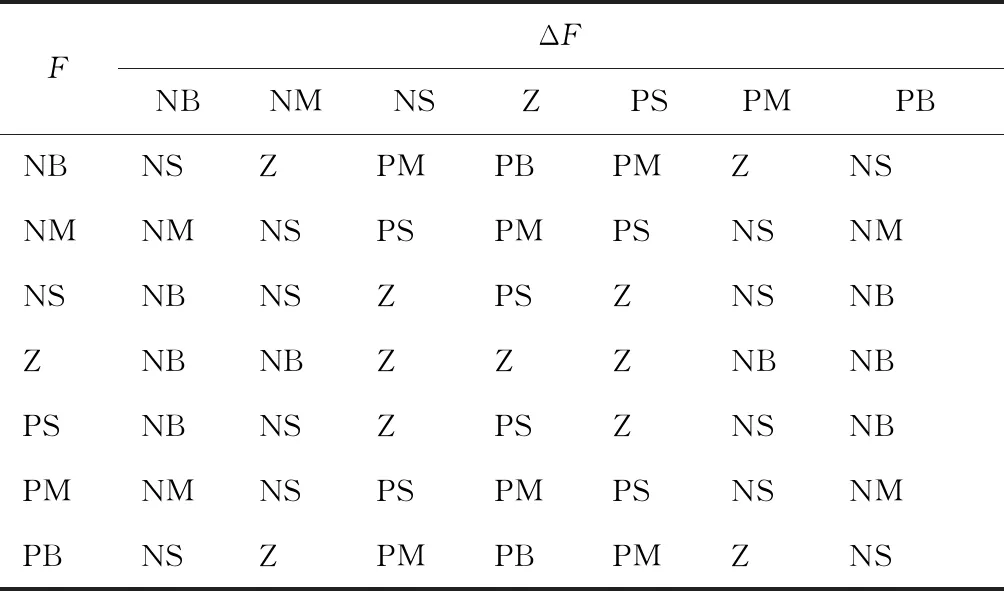
表1 模糊规则Tab.1 Fuzzy rules

表1的特点是根据F和ΔF的值,将负载力划分为不同区间:① 小负载力低速上升;② 中等负载力快速上升;③ 大负载力低速下降.针对液压驱动状态不同,通过模糊规则实现对负载力的自适应调节功能.

采用模糊化求解输出量Δkp,Δki,Δkd的论域变化因子,以变换后的论域[-αpEp,αpEp],[-αiEi,αiEi]和[-αdEd,αdEd]作为模糊PID控制器的输出论域,从而形成双模糊控制器,如图6所示.

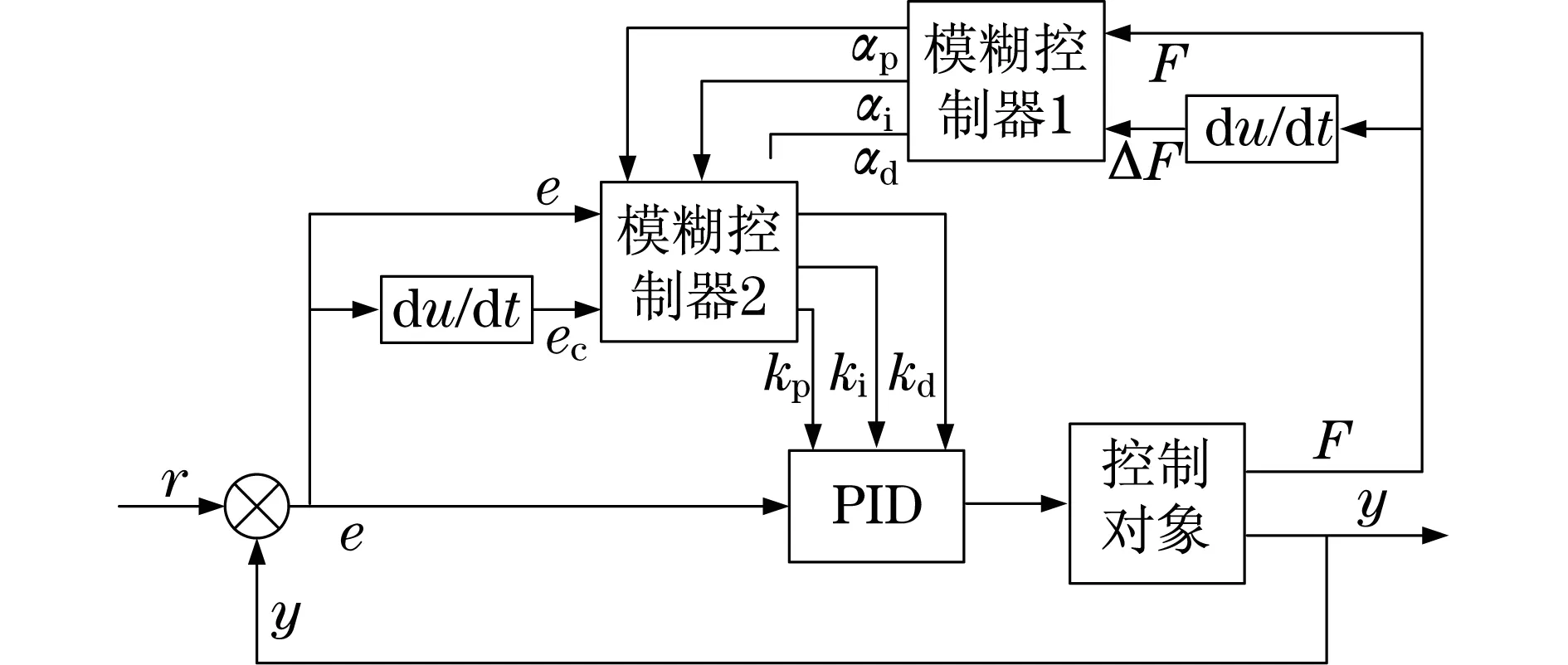
图6 双模糊控制器Fig.6 Double fuzzy controller

3 仿真与分析

偏导射流式压力伺服阀采用双模糊控制结构,通过Matlab对液压双模糊控制系统进行仿真验证.仿真参数设置如下:供油压力为p=21 MPa,流量为Q=30 L/min,线圈电阻R=50 Ω,输入电压信号为U=0.75 V,跟踪信号为y=100 sin(2πt) mm.采用Matlab软件分别对PID控制和双模糊控制器进行仿真.伺服阀在受到不同负载作用力下,其位移跟踪误差仿真结果分别如图7、图8及图9所示.

图7 误差e1仿真曲线(Fmax=50 kN)Fig.7 Simulation curve of e1 error (Fmax=50 kN)

图8 误差e2仿真曲线(Fmax=100 kN)Fig.8 Simulation curve of e2 error (Fmax=100 kN)

图9 误差e3仿真曲线(Fmax=150 kN)Fig.9 Simulation curve of e3 error (Fmax=150 kN)

由图7可知,液压驱动控制在受到最大负载力为50 kN时,PID控制和双模糊控制产生的误差都在1 mm以内;由图8可知,液压驱动控制在受到最大负载力为100 kN时,PID控制产生的误差在2 mm以内,而双模糊控制产生的误差在1 mm以内;由图9可知,液压驱动控制在受到最大负载力为150 kN时,PID控制产生的误差在4 mm以内,而双模糊控制产生的误差在1 mm以内.综合比较可得,双模糊控制能够抑制外界最大负载力的干扰,提高液压驱动跟踪精度,从而提高刹车控制系统的稳定性.

4 结论

本文采用双模糊控制器用于偏导射流式压力伺服阀驱动控制,主要结论如下:① 偏导射流式压力伺服阀采用双模糊控制方法,其跟踪误差降低,误差整体波动幅度较小;② 双模糊控制方法实现对负载力的自适应调节功能,抑制负载力变化的干扰,具有较好的跟踪效果.