人工岩心电频谱实验及饱和度评价模型研究

马雪瑞，柯式镇*，贺秋利，李君建，蔡亚琳

1 中国石油大学(北京)地球物理学院，北京 102249

2 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

3 中国石油集团测井有限公司，西安 710077

4 上海石油天然气有限公司，上海 200041

0 引言

岩石的电阻率随着测量电流频率变化而变化的现象称之为岩石的电频散现象。常规电阻率测井通过Archie公式在油气评价中发挥了重要作用[1]。电频谱测井是基于岩石的电阻率频散现象发展起来的一种新的测井方法，其测量结果能够包含地层丰富的信息。但由于岩石电阻率频散的微观机理还没有形成统一的认识[2]，电频谱测井的发展受到了很大的限制，因此急需开展此方面的研究。

上个世纪国内外的研究学者就已经对岩石的电阻率频散特性给予了很多关注，由于测量条件的影响，研究学者对岩石电阻率性频散的测量多在几千赫兹及以下，并不能完整的观察到完整的电阻率频谱，且研究学者较为关注岩石的介电特性或岩石电导率的频散与黏土含量或者CEC之间的关系[3-6]。新世纪以来，研究学者在较宽的频率范围内研究了岩石复电阻率与润湿性[7-8]，渗透率[9-14]等参数的关系，但是这些研究多只关注岩石复电阻率与某一种或者两种因素的关系。Revile研究团队近年对岩石复电导率的研究较多，但其研究频率为超低频，更关注岩石的激发极化效应[12-13]。而在应用复电阻率频谱解决实际地层问题方面，也有很多学者进行研究。郭立新在2009年，结合油田实际情况，定性分析了复电阻率测井基于高低频电阻率比值所建立的解释模型的应用效果，但该研究只是对复电阻率饱和度模型进行了定性分析[14]；宋延杰等利用与有效介质对称各向异性导电理论所建立的复电阻率解释模型，在水淹层解释方面应用良好，但只针对了两个频率点进行探索[15]。近年来，对于复电阻率解释模型的研究很多，但大多数都停留在定性分析的阶段，或只在单一频率下进行探讨，没有充分考虑到扫频测量条件下岩样的频散情况。在前人对岩样复电阻率频散特性的研究中，Cole-Cole模型可以很好的表征岩样的频散特性。但对于Cole-Cole模型中参数的研究还处于理论阶段，没有将其与地层参数建立联系。

本文在 40 Hz～110 MHz范围内测量了人造岩心的电阻率，考察了孔隙度、含水饱和度、矿化度、离子类型、温度、黏土含量对岩心电阻率频散特性的影响，利用Cole-Cole模型拟合实验曲线并获得了1 kHz电阻率与时间常数，研究了1 kHz电阻率和时间常数与各个影响因素的关系。同时，结合实验数据定量的建立了Cole-Cole模型与地层参数之间的关系，即本文所建立的电频谱饱和度解释模型，并将模型模拟结果与天然岩心测量数据进行对比分析。

1 实验过程

为考察各影响因素对岩石电阻率频散特性的影响，本次实验采用人造岩心，包括4块纯砂岩和2块泥质砂岩，本文所用到的岩心的参数如表1所示岩心均加工为直径25 mm的柱塞状，长度不小于3 cm。岩心分别饱和2.5 kppm、10 kppm、100 kppm的NaCl溶液和CaCl2溶液。测量过程分为两部分，一是常温下在油驱水过程中进行岩石的电频谱测量，利用煤油进行驱替，最小驱替速率为0.01 mL/min，围压保持10 MPa恒定，计量岩石出水量；驱替结束后将岩心置于恒温箱的夹持器中，改变恒温箱的温度，在20 ℃～80 ℃范围内测量岩石的复电阻率。实验均采用二极法进行测量，测量仪器为HP4294A阻抗分析仪，测量频率范围为 40 Hz～110 MHz。

表1 岩心数据参数表Table 1 Sample parameters

2 数据处理与参数反演

2.1 数据处理

实验测量过程中，由于测量阻抗值较大，加上环境干扰，实验数据引入了很多高频噪声，需要对实验数据进行去噪处理。小波变换在信号处理中有着广泛的应用，在去除噪声方面，小波变换可以进行多尺度分析，有着良好的去噪效果[16]。

信号f(x)的小波变换表示为：

其中，ψ(t)为基小波，a为伸缩因子，b为平移因子。本文采用的基小波为Morlet小波，在小波域中利用阈值去噪法将高频噪声去除，采用小波变换中常用的Mallat算法进行分解和重构。

图1为去噪前后的数据，所用数据为1-3号岩心数据的处理结果，孔隙水矿化度为2.5 kppm,离子类型为CaCl2。

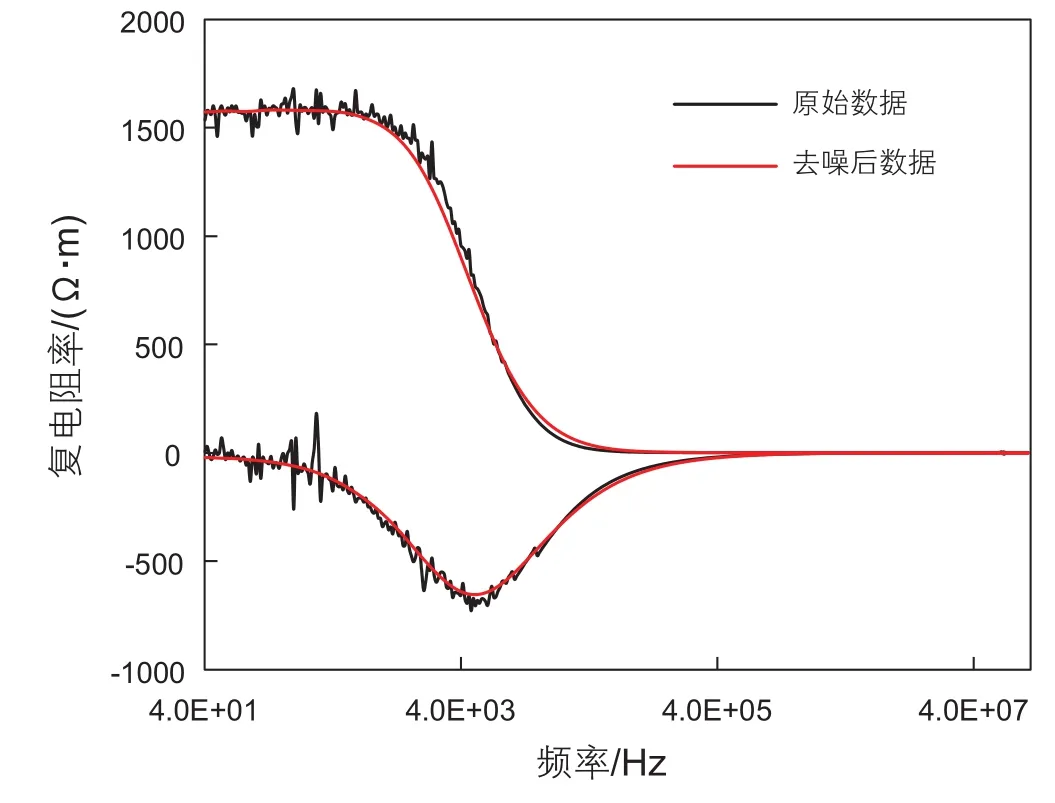
图1 去噪后的数据与测量数据Fig. 1 Denoised data and measurement data

2.2 参数反演

利用岩石物理实验数据反演结果对解释模型进行标定是复电阻率测井资料解释的基础，反演方法的选择会对反演结果及其准确性产生影响，林小稳，柯式镇等比较了最小二乘法、模拟退火算法以及遗传算法在反演Cole-Cole模型参数及实测数据方面的优缺点，发现模拟退火算法在岩石复电阻率参数反演中，因其不依赖初值能够得到全局最优解，过程简单，容易实现等优点，被广泛使用[17-18]。

岩石电阻率随频率的变化可以表示为[18]：

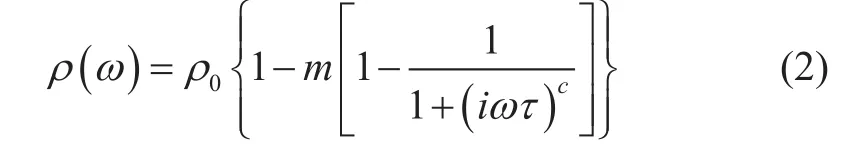
其中，ρ(ω)为复电阻率，Ω⋅m；ρ0为1 kHz率时岩石电阻率，Ω⋅m；m为极化率；τ为时间常数，c为频率相关系数，ω为角频率

在模型的选择方面，Dias模型和基于二阶乘积形式的Cole-Cole模型的拟合效果差不多，但由于其所涉及到的参数太多，应用在实际解释中，意义不大，故选择基于乘积形式的二阶Cole-Cole模型(公式3)更具有优势，

式中各参数意义与一阶Cole-Cole模型中参数意义相同。

本文基于乘积形式的二阶Cole-Cole模型，利用模拟退火算法得到各个模型参数，如图2所示，本次研究主要关注时间常数τ2(后文表示为τ)。

3 实验结果

3.1 频率的影响

图3为测量的岩石复电阻率的实部和虚部。在40 Hz～110 MHz之间，复电阻率实部随频率的升高先缓慢下降，而后迅速下降，在6 MHz左右减小为0；起初，复电阻率虚部随频率升高略有升高，而后逐渐下降，达到最小值后逐渐上升并趋于0。低频时，虚部值略有上升是由于电极极化引起的。

通常，将复电阻率虚部最小值对应的频率定义为界面极化频率fc，且反演出的时间常数与界面极化频率的关系为[19]：

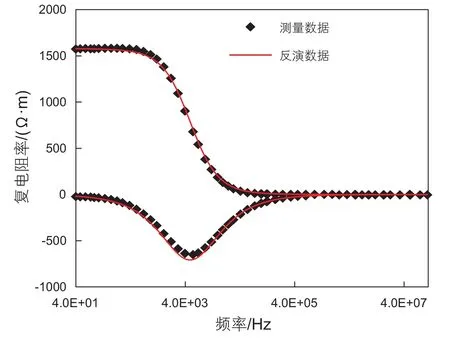
图2 反演结果与实验数据Fig. 2 Inversion data and measurement data

3.2 孔隙度的影响

由Archie公式可知，当其他条件一定时，孔隙度φ越小，地层电阻率R0越大[1]。图4为饱含2.5 kppmCaCl2溶液时，不同孔隙度的纯砂岩岩心复电阻率与频率的关系，从图中可知随着孔隙度的减小，岩石的频散程度增强，实部和虚部电阻率增大，虚部谷底频率减小。

岩石导电主要依靠岩石孔隙空间中的矿化水。当岩石的孔隙度减小，岩石孔隙空间减小，孔隙水中所含离子数目减小，使得岩石导电能力减弱，电阻率上升；同时，孔隙水中离子数目的减少，也直接导致了孔隙空间中离子发生极化时间的减小，虚部谷底频率增大，时间常数减小。

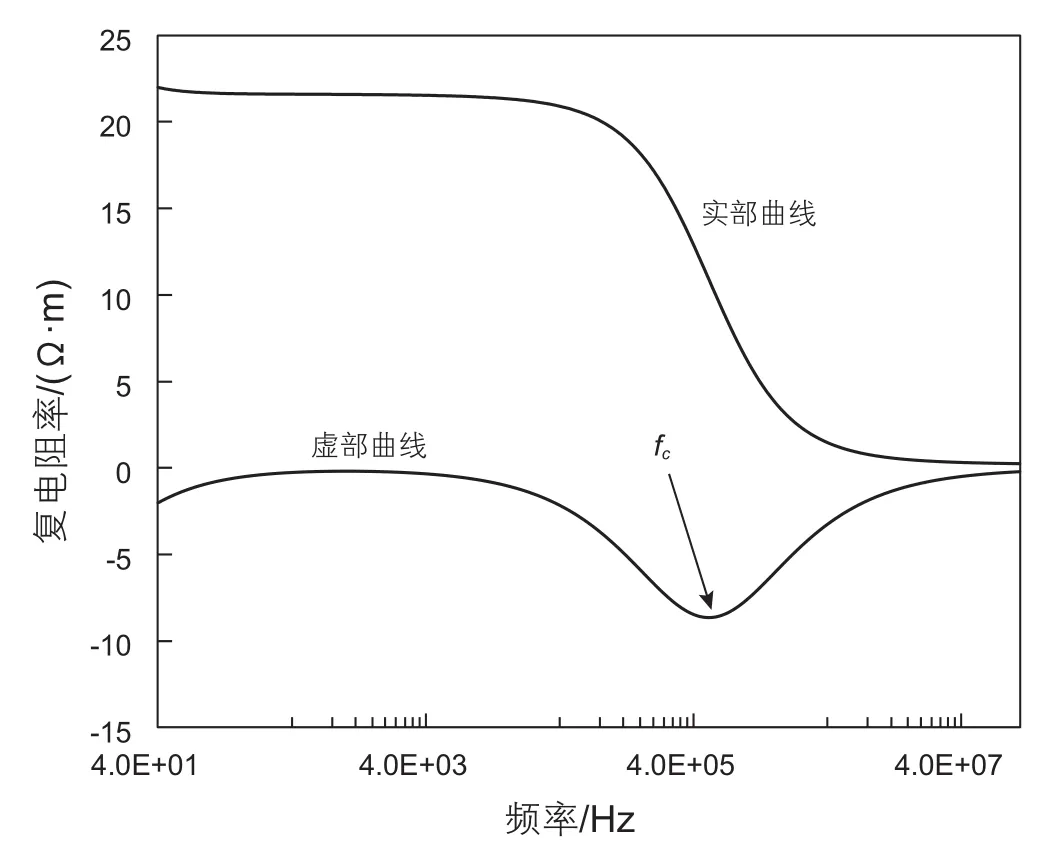
图3 典型岩心电阻率频散曲线Fig. 3 Typical core resistivity dispersion curves

3.3 含水饱和度的影响

由Archie公式可知，对于含油的岩石，当其他条件一定时，岩石的电阻率随着含水饱和度的减小而增大[1]。图5为孔隙水是10 kppmNaCl溶液时，不同含水饱和度的1-2号纯砂岩岩心复电阻率。由图可知，岩心复电阻率实部和虚部随着含水饱和度的减小而增大，虚部谷底频率随含水饱和度的减小而减小。

同孔隙度的影响相似。随着含水饱和度的降低，当岩石孔隙空间中导电的水被不导电的油占据，导电通道减小，岩石孔隙水中所含离子数目减少，岩石的导电能力下降，电阻率升高；同时，孔隙水中离子数目减小，导致离子发生极化的时间增大，故岩石的时间常数随着含水饱和度的降低而增大，谷底频率向低频方向移动。

图4 不同孔隙度的纯砂岩岩心电阻率频散曲线(a)实部曲线；(b)虚部曲线Fig. 4 Resistivity dispersion curves of pure sands with different porosity (a)curves of the real part, (b)curves of the imaginary part

3.4 温度的影响

图6为饱含100 kppmNaCl溶液的1-1号岩心在不同温度下的岩心电阻率频散曲线。在实际地层中，埋藏越深，地层的温度越高。从图中可以看出岩心实部电阻率和虚部电阻率均随温度的升高而减小，同样，1 kHz电阻率和时间常数也随温度的升高而减小。因为温度越高，岩石孔隙水中的离子运动速率加快，导致岩心导电能力增强，岩心电阻率减小；同时，离子运动速率变大，使得发生极化的时间减小，时间常数随温度的升高而减小，谷底频率向着频率增大方向移动。

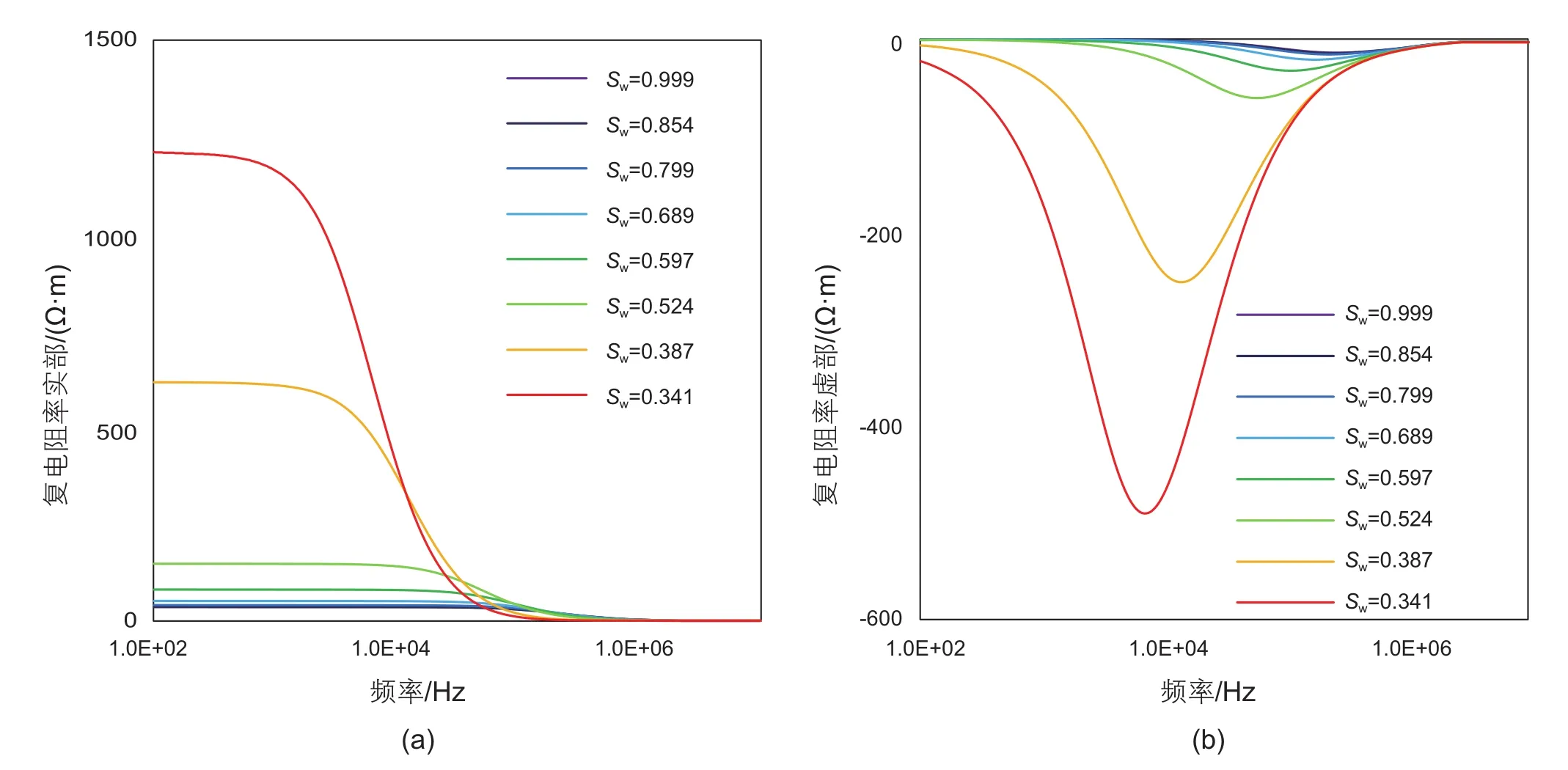
图5 不同含水饱和度的纯砂岩岩心电阻率频散曲线(a)实部曲线；(b)虚部曲线Fig. 5 Resistivity dispersion curves of pure sands with different water saturation (a)curves of the real part, (b)curves of the imaginary part

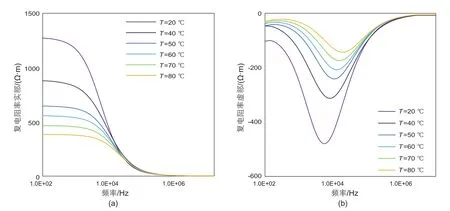
图6 不同温度下1-1号岩心电阻率频散曲线(a)实部曲线；(b)虚部曲线Fig. 6 Resistivity dispersion curves of the 1-1 sample at different temperature (a)curves of the real part, (b)curves of the imaginary part

3.5 矿化度的影响

岩心孔隙水的矿化度对岩石的导电性有很大的影响。图7为1-2号岩心在完全饱和不同矿化度NaCl溶液的岩心电阻率频散曲线。从图中可以看出，随着孔隙水矿化度的升高，岩石电阻率频散程度减小，岩石复电阻率实部和虚部电阻率减小，虚部谷底频率增大。

由于矿化度的升高，岩石孔隙水中导电离子数目增多，孔隙水导电能力增强，导致岩石电阻率下降；同时，孔隙水中离子数目的增多，使得在一定的孔隙空间内发生极化的时间减小，所以弛豫时间随矿化度升高而减小，谷底频率向着频率增大的方向移动。

图7 1-2号岩心在完全饱和不同矿化度NaCl溶液的岩心电阻率频散曲线(a)实部曲线；(b)虚部曲线Fig. 7 Resistivity dispersion curves of the 1-2 sample saturated with NaCl solution with different salinity (a)curves of the real part, (b)curves of the imaginary part

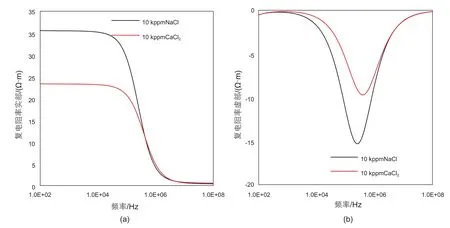
图8 相同矿化度下饱含NaCl溶液和CaCl2溶液的岩心电阻率频散曲线(a)实部曲线；(b)虚部曲线Fig. 8 Resistivity dispersion curves of a sample saturated with NaCl solution and CaCl2 solution with same salinity (a)curves of the real part, (b)curves of the imaginary part

3.6 离子的影响

从图8中可以看出，相同矿化度下，饱含CaCl2溶液的岩心电阻率频散程度更大，电阻率阻值更高，虚部谷底频率更小，时间常数更大。因为在矿化度单位同为ppm(mg/L)时，CaCl2的分子量更大，故等量的溶液中CaCl2溶液的离子数较少，且CaCl2溶液与NaCl溶液中电荷量基本相当。因此饱含CaCl2溶液的岩心电阻率较高。由于钙离子半径更大，迁移速率较低，故时间常数较大，界面极化频率较低。

3.7 黏土含量的影响

图9中涉及的三块岩心是1-2号纯砂岩岩心，气测孔隙度为17.27%；岩心编号为4-1的含有10%伊利石的泥质砂岩岩心，气测孔隙度为16.57%；岩心编号为4-2的含有20%伊利石的泥质砂岩岩心，气测孔隙度为17.63%。随着黏土含量的增加，岩心电阻率频散程度降低，实部电阻率和虚部电阻率均减小，虚部谷底频率向频率增大的方向移动。同样，随着黏土矿物含量的增加，岩石电阻率与时间常数有所减小。

由于黏土矿物离子双电层的附加导电性[21]，使得含有泥质的砂岩电阻率较同等情况下砂岩电阻率较低。在一定的含量范围内，岩石电阻率随岩石含黏土矿物含量的增大而减小。同时，泥质砂岩中，极化是由界面极化和离子双电层极化共同组成[22]，且界面极化的影响大于离子双电层形变的影响。在电场的作用下，离子双电层发生形变，电场反方向一侧积累较多负电荷，沿电场方向积累较多正电荷，黏土矿物颗粒附着在孔隙壁两侧，自由水中的正负离子为抵消离子双电层形变的影响，一部分电荷被中和掉了，故界面极化效应减弱，使得在同样的电场强度下整体极化强度减小，离子恢复平衡的时间减小，导致时间常数减小，界面极化频率向着频率增大方向移动。。

3.8 反演结果分析

本文将实验所测得的数据基于乘积形式的二阶Cole-Cole模型进行拟合，并利用模拟退火算法得到时间常数τ，探究了各影响因素对时间常数以及1 kHz情况下岩石实部电阻率的影响。

图10～图11分别为纯砂岩岩心含水饱和度和孔隙度的改变对1 kHz电阻率和时间常数的影响。从图中可以看出，随着含水饱和度和孔隙度的增大，1 kHz电阻率和时间常数均呈幂指数形式衰减。随着含水饱和度和孔隙度的增大，孔隙中可以自由移动的离子数目增多，使得整个岩样的导电性增强，引起电导率升高，电阻率降低，而且离子数目的增多，极大的减少了岩石内部的极化时间，使得时间常数减小。

图9 孔隙度相似且泥质含量不同的岩心电阻率频散曲线(a)实部曲线；(b)虚部曲线Fig. 9 Resistivity dispersion curves of samples with similar porosity and different clay contents (a)curves of the real part, (b)curves of the imaginary part

图12为泥质砂岩的含水饱和度的改变对1 kHz电阻率和时间常数的影响。从图中我们可以看出，与纯砂岩类似的，含水饱和度的改变对电阻率和时间常数的影响规律也十分相近。

经上述分析，在实验的过程中，结合虚部实验数据和频率的关系，发现在频率不为零的时候，时间常数满足如下经验公式：

其中，ρ0为岩石在1 kHz条件下的电阻率，Pτ和Qτ均为常数。

4 电频谱测井饱和度模型

岩石复电阻率频散特性的研究对建立电频谱测井饱和度模型至关重要，由于外加电场以及孔隙流体的存在，会使岩石呈现阻抗和容抗的特性。而Cole-Cole模型可以描述激发极化效应以及描述低频部分，复电阻率频散响应可以表示为多个Cole-Cole模型的组合，该模型能够很好的拟合复电阻率曲线。模型可以表达为：

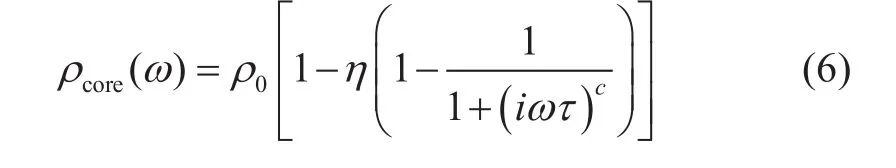
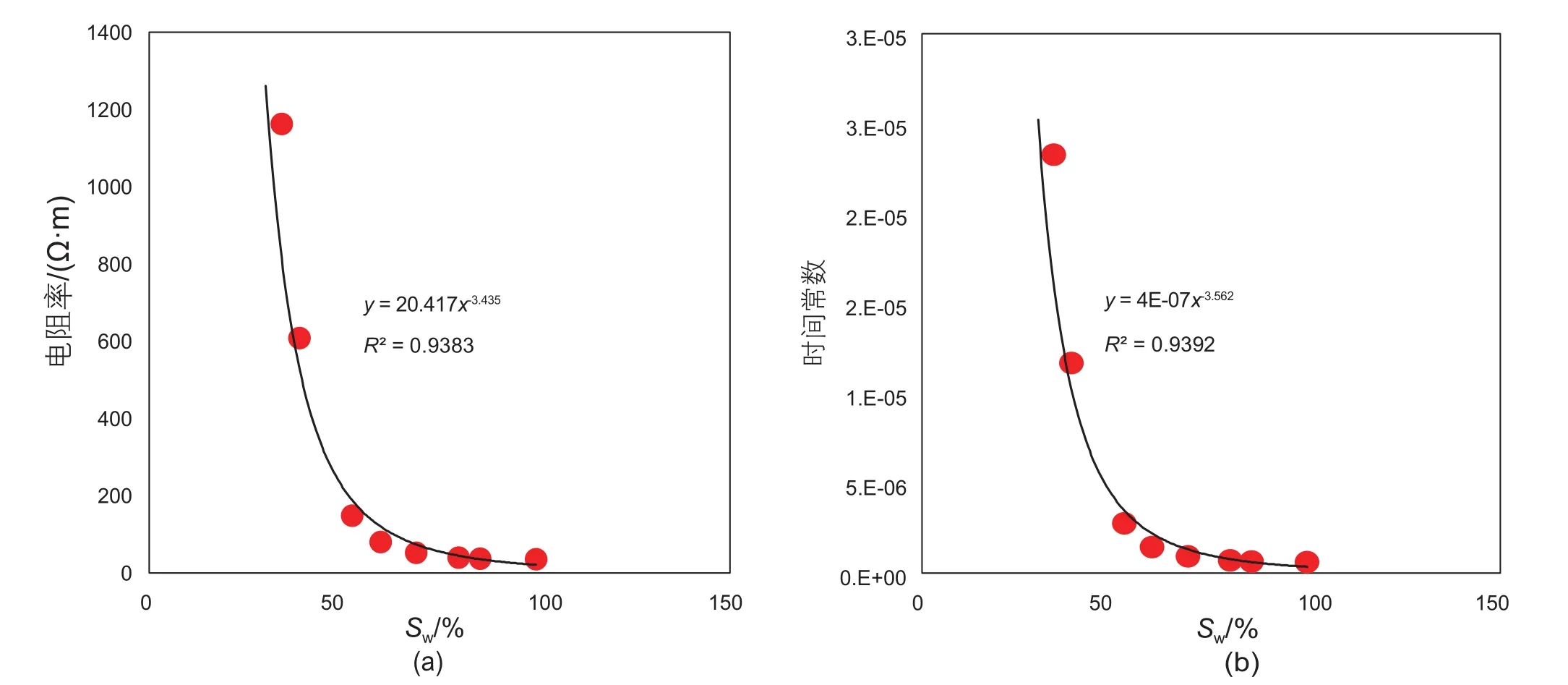
图10 纯砂岩的1 kHz电阻率和时间常数与含水饱和度的关系(a)电阻率曲线；(b)时间常数曲线Fig. 10 1 kHz resistivity and time constant of pure sandstone with different water saturation (a)curve of resistivity, (b)curve of time constant

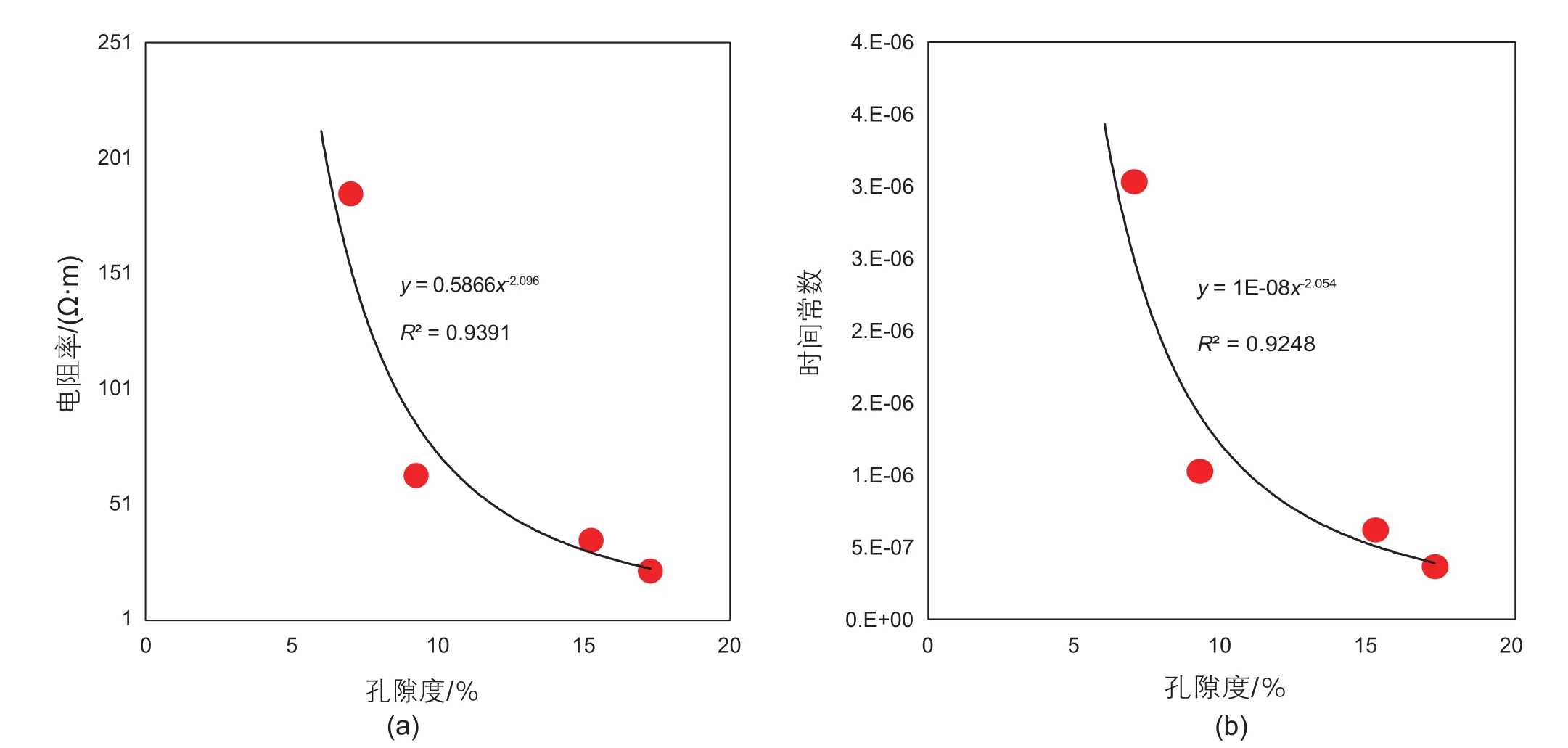
图11 纯砂岩的1 kHz电阻率和时间常数与孔隙度的关系(a)电阻率曲线；(b)时间常数曲线Fig. 11 1 kHz resistivity and time constant of pure sandstone with different porosity (a)curve of resistivity, (b)curve of time constant

其中，ρ0为零频电阻率；η为极化率，0＜η＜1；ω为角频率；τ为时间常数，c为频率相关系数，0 ≤c≤ 1。

在电流频率为零时，即在直流条件下，岩石的电阻率ρ0满足阿尔奇公式，则有：fc为谷底频率；

而通过式(5)我们可以将时间常数与电阻率建立联系。

综上，本文将Cole-Cole模型参数与地层参数建立关系：

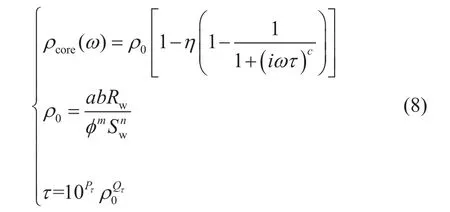
根据以上建立的模型，模拟了岩心复电阻率与含水饱和度、孔隙度、温度、矿化度的关系。从图13～图16中可以看出，随着影响因素的改变，模拟的曲线的变化趋势与前文实验中所得到的结果吻合情况良好，说明该模型能够很好的表征Cole-Cole模型参数与地层参数之间的关系。

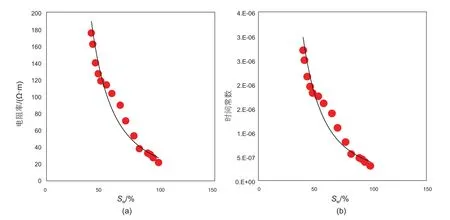
图12 泥质砂岩的1 kHz电阻率和时间常数与含水饱和度的关系(a)电阻率曲线；(b)时间常数曲线Fig. 12 1 kHz resistivity and time constant of shaly sandstone with different water saturation (a)curve of resistivity, (b)curve of time constant

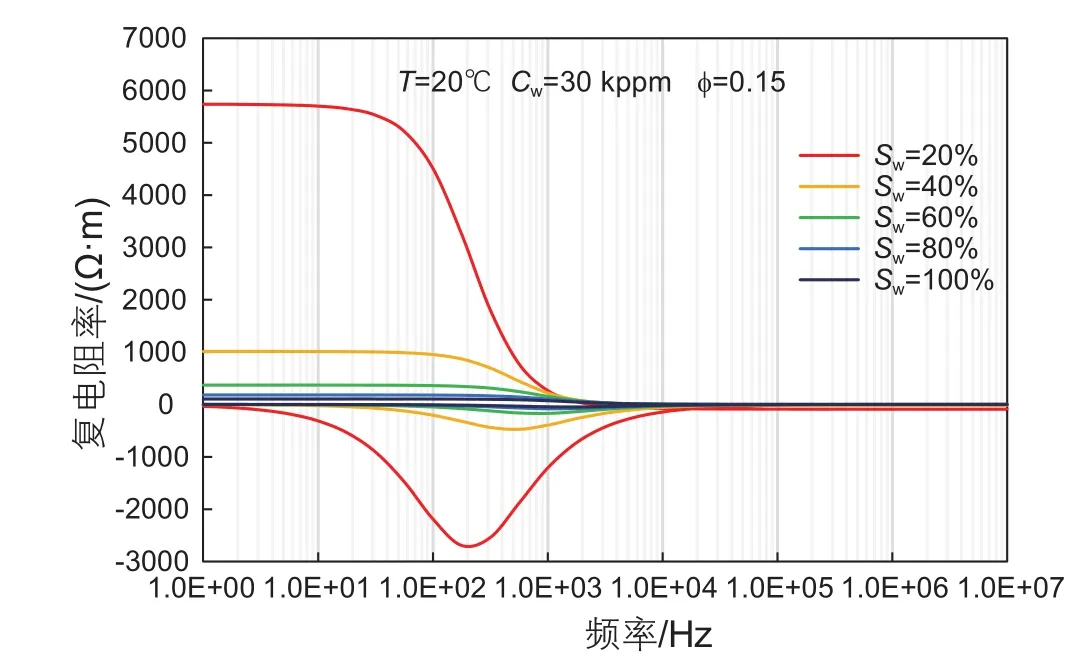
图13 模拟的不同含水饱和度下的岩心复电阻率Fig. 13 Simulation of core complex resistivity with different water saturations

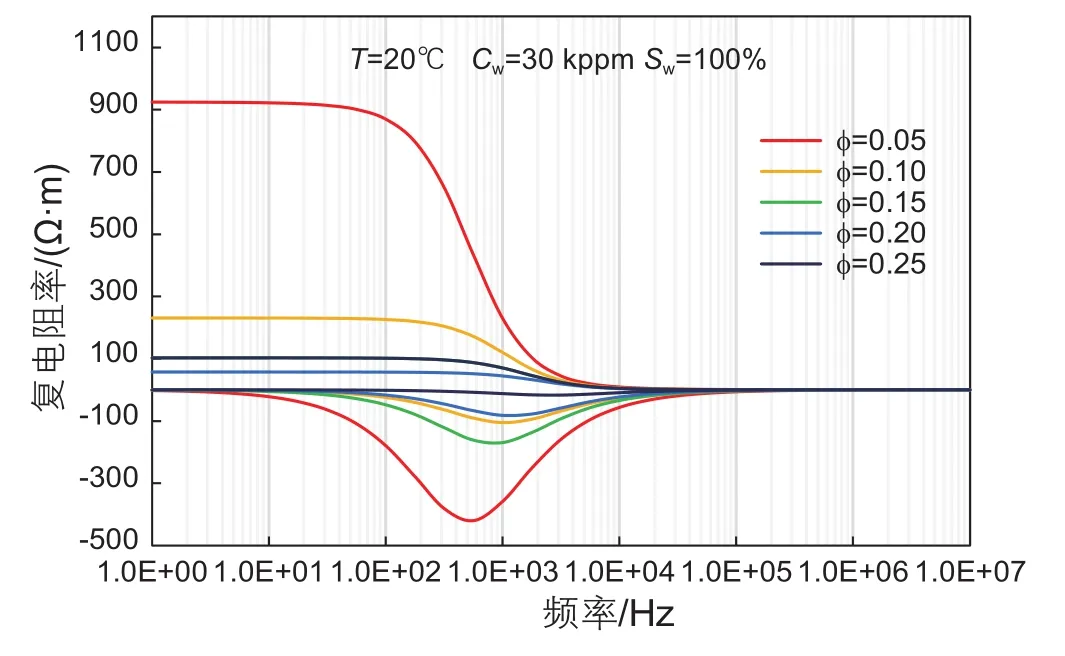
图14 模拟的不同孔隙度下的岩心复电阻率Fig. 14 Simulation of core complex resistivity with different porosity

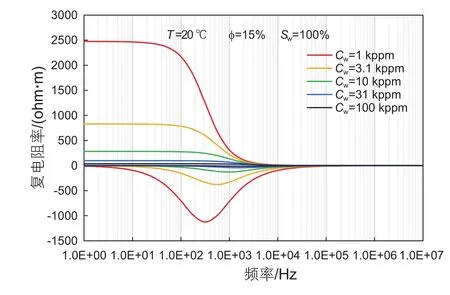
图15 模拟的不同矿化度下的岩心复电阻率Fig. 15 Simulation of core complex resistivity with different salinity

图16 模拟的不同温度下的岩心复电阻率Fig. 16 Simulation of core complex resistivity with different temperature

为更好的验证模型的应用效果，本文测量了一块天然纯砂岩岩心的复电阻率频谱，测量环境为常温条件，岩心的孔隙度为27.3%，孔隙水为10 kppm 的NaCl 溶液，利用所推导出的复电阻率频谱解释模型，来对该天然岩心含水饱和度进行预测，图17为利用时间常数所计算出的含水饱和度与岩样实测含水饱和之间的对比图，从图中可以看出，通过模型计算出的含水饱和度与在实验中所测得的岩样的实际含水饱和的基本一致。

在上述的分析中可知，时间常数τ是与虚部谷底频率有关的参数，其值的大小受含水饱和度的影响。而上述模型将时间常数与含水饱和度之间的关系转为定量分析，即在实际应用中，可以通过时间常数的值以及实部电阻率的值同时对含水饱和度进行计算，这样在很大程度上提高了计算的含水饱和度的精度。

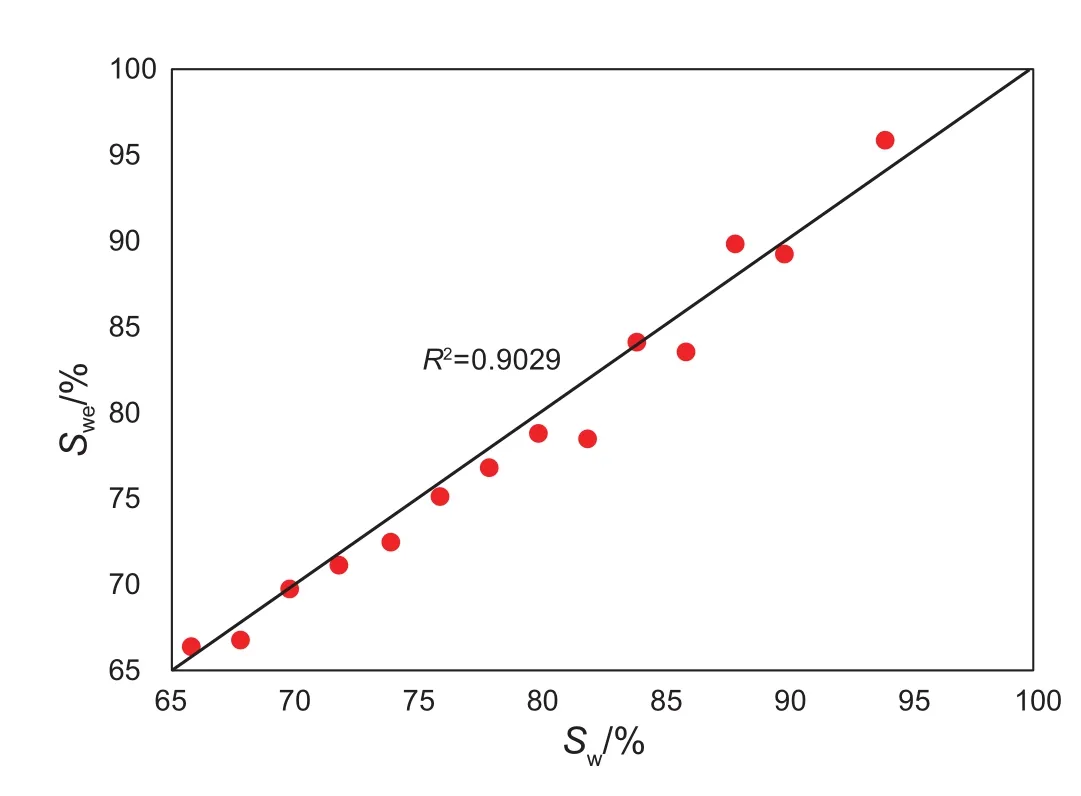
图17 利用时间常数计算的饱和度与测量值对比Fig. 17 Relationship between saturation calculated using time constants and measured values

5 结论

岩心电频谱受孔隙度、饱和度、矿化度、离子类型、温度、黏土含量的影响。随着孔隙度、含水饱和度、矿化度、温度、黏土含量的增大，岩心电阻频散程度减弱，岩心实部电阻率和虚部电阻率均变小。

1 kHz 下电阻率和通过Cole-Cole模型参数反演出的时间常数，二者同样随着孔隙度、含水饱和度、矿化度、温度、黏土含量的增大而减小，整体呈幂函数的衰减形式，而且二者随各个影响因素变化规律相似。

通过电阻率和时间常数，建立Cole-Cole模型中参数与实际地层参数之间的关系，建立了电频谱饱和度解释模型，并应用模型计算数据与人造岩心实验数据和天然岩心实验数据进行相互验证，利用虚部信息反演出的时间常数值所计算出的含水饱和度的值与实际测量值吻合度很高，验证结果表明模型确有可行性。