致密变形介质油藏五点面积井网水驱动态分析

曹耐，董平川*，雷刚

1 中国石油大学(北京)石油工程学院，北京 102249

2 College Petroleum of Engineering & Geoscience, King Fahd University of Petroleum and Minerals, Dhahran 31261, Kingdom of Saudi Arabia

0 引言

致密变形介质油藏的渗流特征与常规油藏的渗流特征显著不同[1-2]，有着其特有的渗流规律，主要表现为2个方面：①孔喉细小、孔喉比大、毛管压力的影响显著，非均质性强，致使流体渗流偏离Darcy定律，出现非线性-拟线性的非Darcy渗流规律[3-4]；②实际生产中，储层骨架产生部分或全部的不可逆变形，岩石渗透率和孔隙度降低[5-6]，对油田的动态特征有明显的影响[7]。而且在实际开发过程中也发现了很多问题：难以形成有效的驱动压力系统，地层压力下降快，产量迅速递减，原油有效动用率低[8-10]。

国内外学者对介质变形理论做了大量研究：Samaniego等考虑岩石应力敏感和流体性质，对储层流体非稳态渗流特征进行了分析[11]。熊建和李凌峰对岩心驱替实验结果进行统计学分析，发现低渗透气藏岩心绝对渗透率随有效应力增加指数下降，并基于此得到了变形介质低渗透气藏产量预测公式[12]。Samimi和Ghorbani等采用无单元数值模拟方法对变形多孔介质中多相流体流动规律进行分析[13-14]。王美楠等结合二次梯度项及动边界理论，对低渗透变形介质油藏渗流规律进行了探讨和分析[15]。郭平和张楠等建立了启动压力梯度和应力敏感效应共同影响下的单井产能模型，并分析了非达西渗流效应对低渗透储层单井产能的影响[16-17]。雷刚等基于致密砂岩气藏中气体非达西渗流特征，考虑储层绝对渗透率应力敏感效应影响，推导了致密砂岩在拟稳态流动阶段的垂直裂缝井产能方程[18]。Pesavento等对变形介质中多相流动研究进行了总结和分析[19]。

然而，上述研究工作基本上都以岩心实验、介质变形系数对单井产能和渗流规律影响为研究目标；针对致密油藏面积井网，考虑介质变形影响的研究却不多[20-22]。齐亚东等建立了特低渗透断块油藏不规则三角形井网有效动用系数计算模型，并以某特低渗透断块油藏为例，对不规则三角形井网有效动用系数进行了计算分析[23]。吕栋梁等建立了低渗透油田反九点井网面积波及效率数学模型[24]。郭粉转等考虑启动压力梯度影响，建立数学模型对低渗透油田四点井网和五点井网面积波及效率进行了计算和分析[25-26]。上述研究工作对于分析低渗透油藏面积井网流动规律具有重大意义，但由于上述文献并未考虑储层的介质变形，建立的理论模型不适于变形介质油藏面积井网生产动态分析，需增加对变形介质油藏面积井网的研究及讨论。因此，从渗流理论上揭示变形介质油藏井网的流动特征是提高油藏原油有效动用率亟待解决的首要问题之一。

笔者充分考虑致密油藏油水两相渗流的非线性特征及多孔介质变形特征，推导了考虑介质变形面积井网的地层压力、势函数、流函数和平面速度计算表达式，根据物质平衡理论及特征线方法，得到考虑介质变形系数面积井网单元流场分布、油藏波及系数、见水时间和剩余油饱和度分布等生产指标，并研究了不同介质变形系数对油藏生产影响。

1 致密介质变形模型驱替理论

建立考虑介质变形油水两相渗流数学模型的假设条件为：①水平均质等厚的无限大地层布有无限延伸的五点井网；②地层只有油水两相，流体在多孔介质中流动均为二维流动；③不考虑毛管压力影响；④油井以定液量生产，注入井注入量与油井产液量相等；⑤多孔介质发生变形，储层渗透率随压力发生变化，而孔隙度随压力变化较小不予考虑。

根据基本假设条件，可以得到多孔介质中油水两相流体控制方程为：

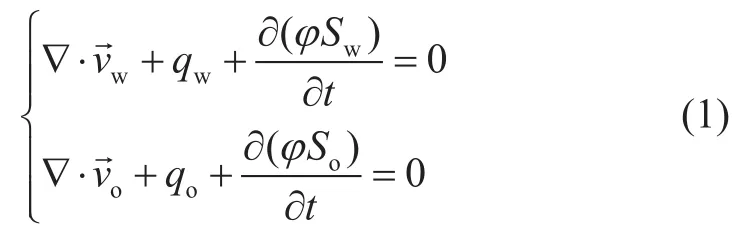
油水两相速度方程分别为：

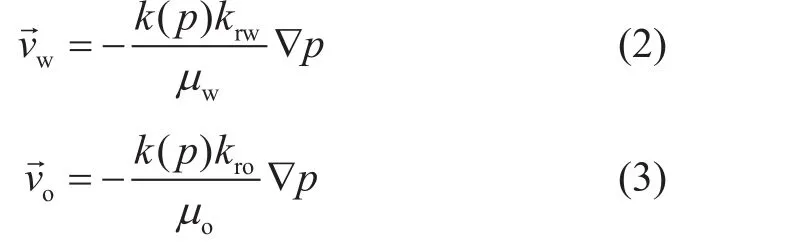
式中k(p)为岩石绝对渗透率。研究结果表明k(p)为岩石孔隙结构、弹性模量和泊松比等参数的函数。目前，国内外学者主要采用指数函数来表征岩石绝对渗透率随有效应力的变化规律[27-28]，关系表达式为：

将方程(1～4)联立并整理(qw+qo=0)，可以得到：

基于不变流线假设，计算地层压力场时，不考虑流度在空间上变化，方程(5)可以变形为：

其中

2 模型计算

2.1 压力计算

方程(6)为调和方程，采用叠加原理，计算无限大地层矩形5点井网稳态压力分布。如图1所示，根据所建立直角坐标系可以得到，油井坐标为(2nd+md,ma)，注入井坐标(2nd+md+d,ma)，其中(m=0，±1，±2，...；n=0，±1，±2，…)。对于地层中任意点M(x,y)，第m排井排中第n口油井在M点的拟势函数为：

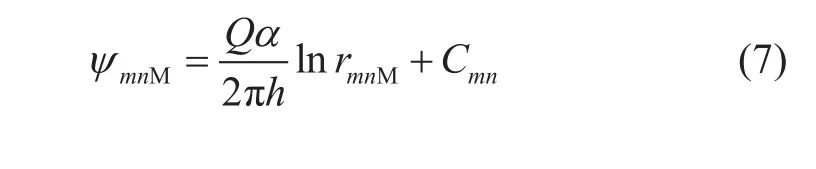
其中

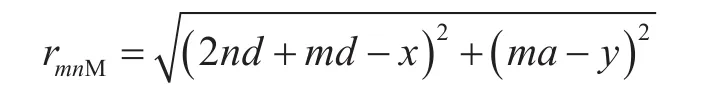
第m排井排中第n口注入井在M点的拟势函数为：

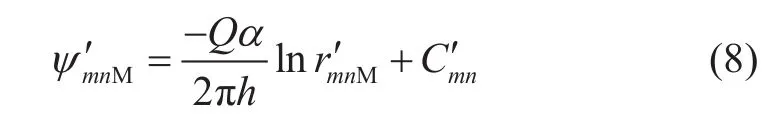
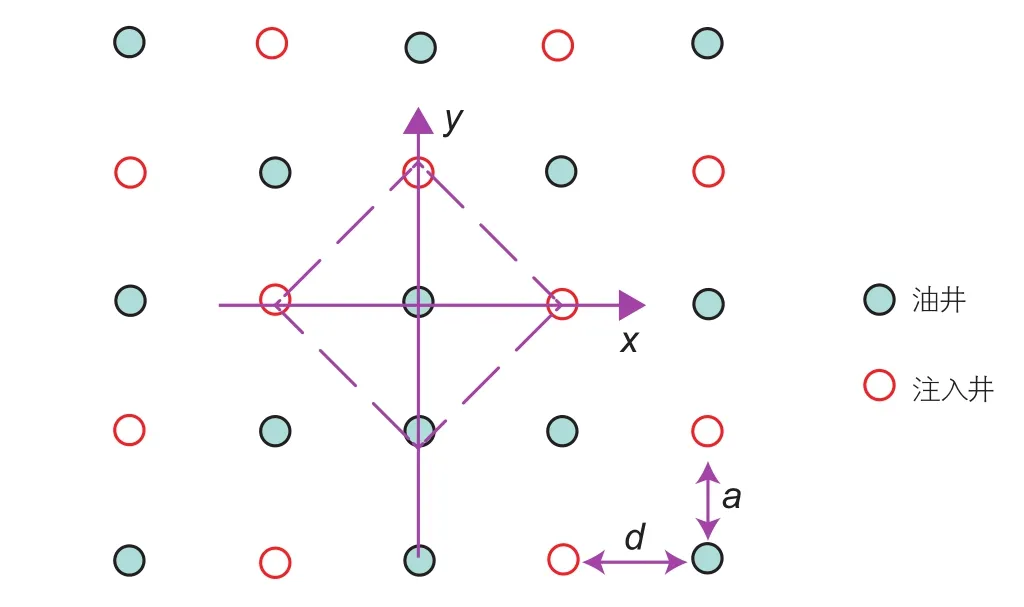
图1 矩形五点面积井网示意图Fig. 1 The sketch map of rectangularfive-spot well pattern

其中

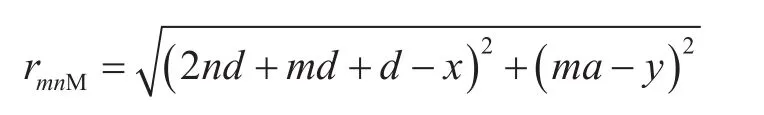
根据势叠加原理，无穷井网在M点拟势函数为：

其中

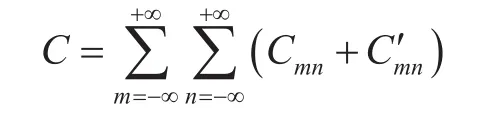
对式(9)进行处理，可以得到：

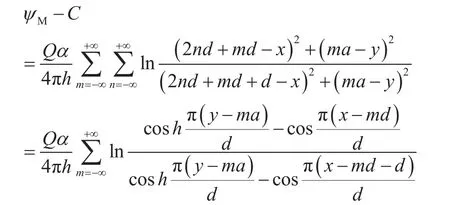
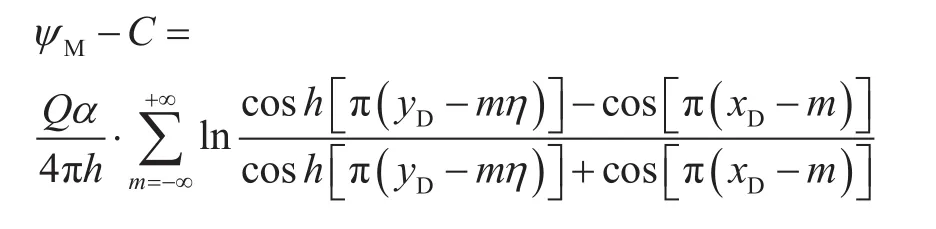
由于ψ=λtU(x,y)，可以得到：

根据无因次压力定义，可以得到地层压力：

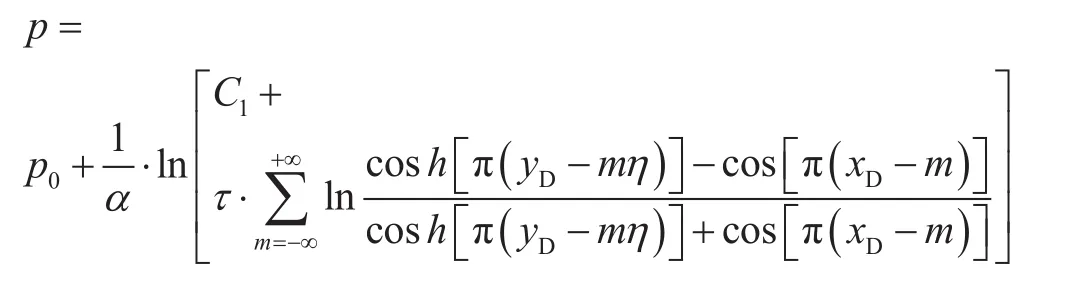
其中

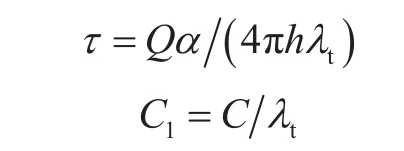
若注入井注入压力为piwf，生产井井底压力为pwf，则根据压力计算公式，可得到无因次注采压差为：

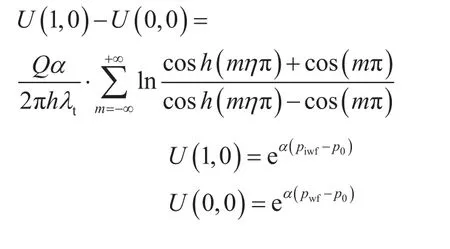
2.2 流函数计算

令vt=vo+vw，由式(2)、(3)、(4)可得：

通过方程(10)可以得到五点面积井网任意位置在x，y方向渗流速度：

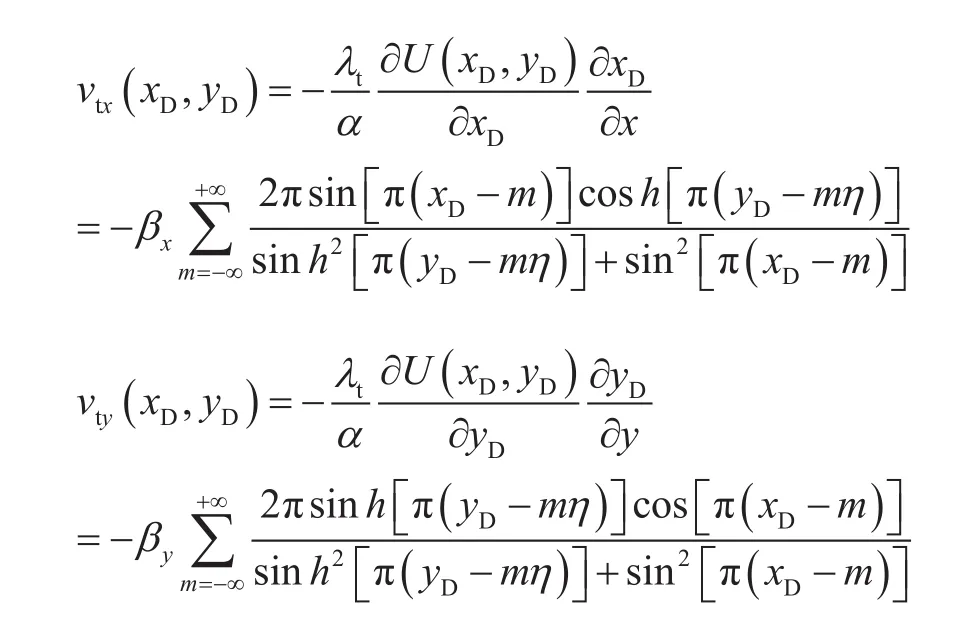
由于dy=adyD，通过对速度积分可以得到流函数为：

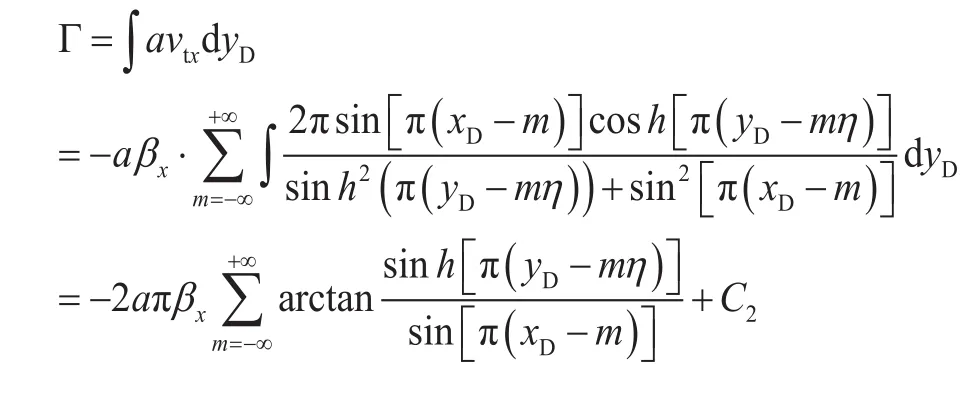
式中：

2.3 有效动用系数计算

对于五点井网，x，y轴上主流线均为直线。主流线任意点在x方向上的渗流速度为：

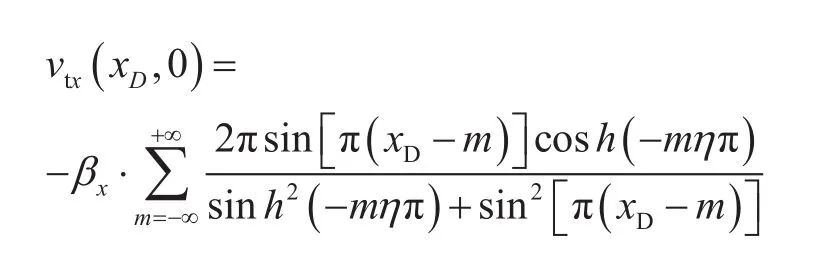
由此可确定x方向上见水时间：

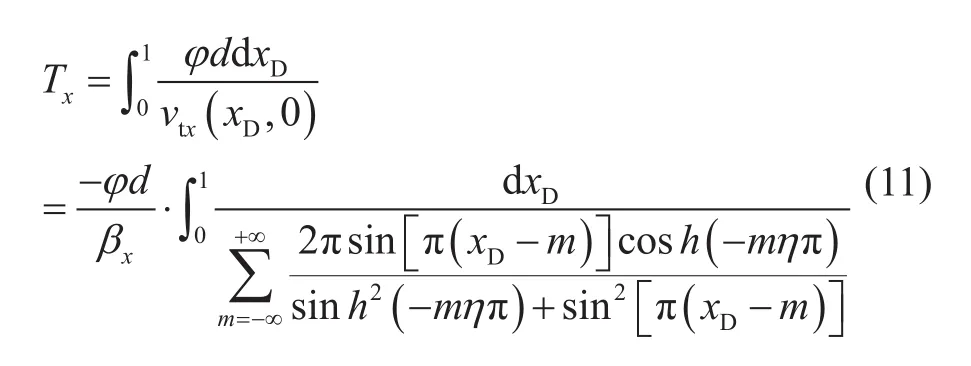
同理可确定y方向上见水时间：

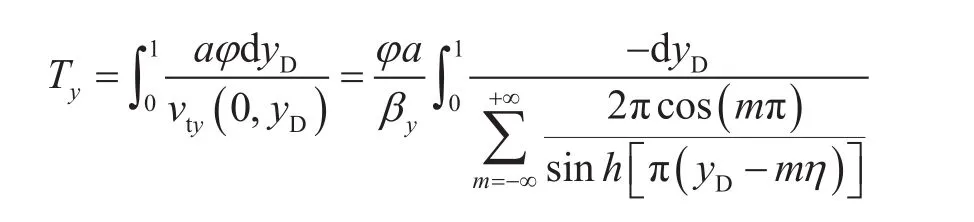
所以可得到见水时间：

根据(12)，并利用物质平衡方法，可得到井网单元有效动用系数为：

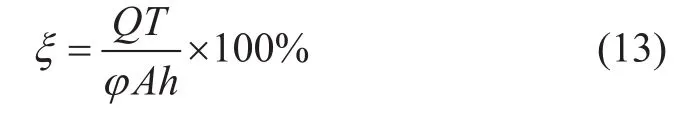
由于地层均质，井网单元有效动用系数即为无穷大面积井网有效动用系数。

2.4 含水饱和度计算

由方程(1)、(10)可得到：

微分方程(14)特征微分方程为：

沿特征线有：

式(16)说明沿特征线含水饱和度不变，即特征线就为等饱和度线。通过式(15)得到等饱和度面运动特征方程：

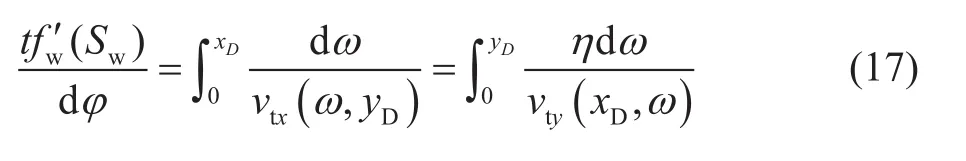
求解特征方程(17)可以得到任意时间地层含水饱和度分布。

3 计算实例

为研究储层有效动用情况，以长庆油田某低渗透砂岩实际储层特性数据及生产数据为例，对推导的数学模型进行了计算。通过室内岩心渗透率应力敏感实验，得到介质变形系数为0.014 MPa-1。计算分析所采用的基础数据如表1所示。

3.1 典型压力场、流场分布

通过计算可以得到地层压力分布如图2、图3所示。图2为地层某区块压力分布，图3为地层某五点面积井网单元压力分布。地层压力场分布图展现了面积井网生产特征，注入井附近区域压力值较高，生产井附近区域地层压力值较低，由于面积井网对称性及地层均质性，地层压力表现为对称分布。

图4为地层某五点面积井网单元流场分布，地层流场分布图展现了面积井网生产特征，近井附近区域流线密，远井附近区域流线疏，主要原因在于近井附近区域生产压差大，从而造成流线密集分布。

3.2 介质变形系数对流场分布的影响

对于不同介质变形系数，在流函数值相等情况下，可得到地层流线分布示意图如图5、图6、图7所示。

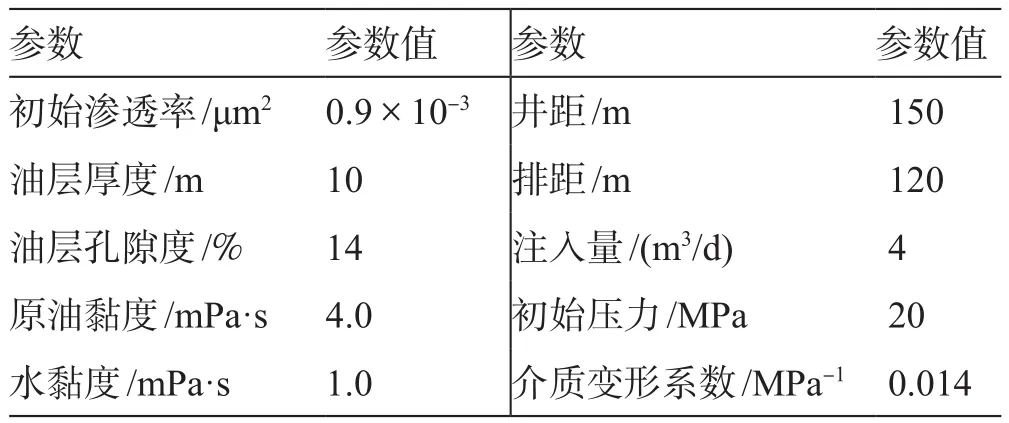
表1 模型基础数据Table 1 The reservoir parameters of the model

图2 区块压力分布(α=0.014 MPa-1)Fig. 2 Pressure field distribution of formation area block(α=0.014 MPa-1)

由图5、图6和图7可见，介质变形系数越大，流线波及面积越小。主要原因在于随着介质变形系数增大，地层渗流阻力增大，渗流速度减小，从而导致流线波及面积减小。

3.3 介质变形系数对见水时间、动用程度的影响

根据得到压力计算公式，对于不同介质变形系数，产量与生产压差关系曲线图如图8所示。

从图8可以看出，随着介质变形系数增大，产量增幅随着生产压差增大而减小。主要原因在于随着生产压差增大，地层渗透率降低，生产阻力变大，从而使得产量与生产压差关系不再满足达西定律。

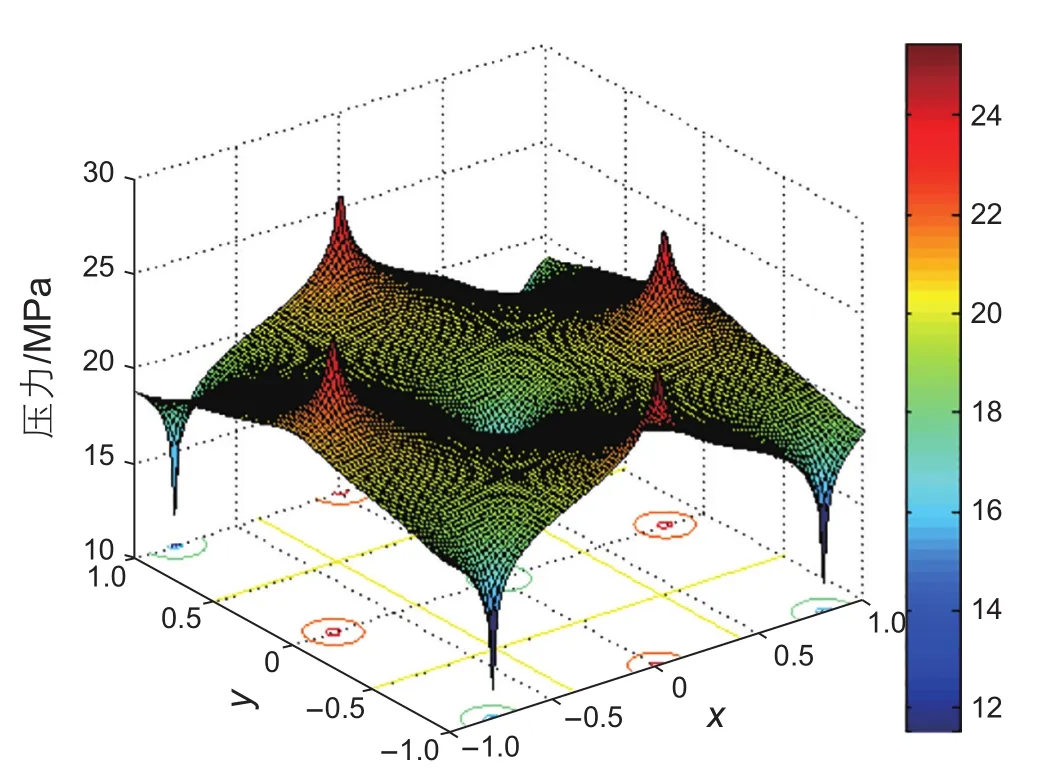
图3 五点面积井网单元压力分布(α=0.014 MPa-1)Fig. 3 Pressure field distribution of five-spot well pattern unit(α=0.014 MPa-1)

图4 五点井网单元流场分布(α=0.014 MPa-1)Fig. 4 Streamline distribution of 5-spot well pattern unit(α=0.014 MPa-1)

通过式(11)、(12)可计算见水时间随介质变形系数变化规律如图9所示。

从图9可以看出，见水时间随介质变形系数增加而增大，说明多孔介质变形增大了渗流阻力，降低了流体渗流速度。

对于本文所给实例，当介质变形系数为0.014 MPa-1时，油井见水时间为149.6 d，现场分析结果显示油井见水时间为166 d，本文计算结果相对误差为9.9 %，符合性较好，说明本文计算模型正确。根据式(13)可计算地层有效动用系数为11.87 %。

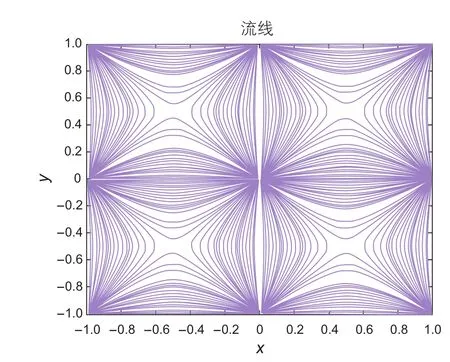
图5 流场分布(α=0.013 MPa-1)Fig. 5 Streamline distribution (α=0.013 MPa-1)

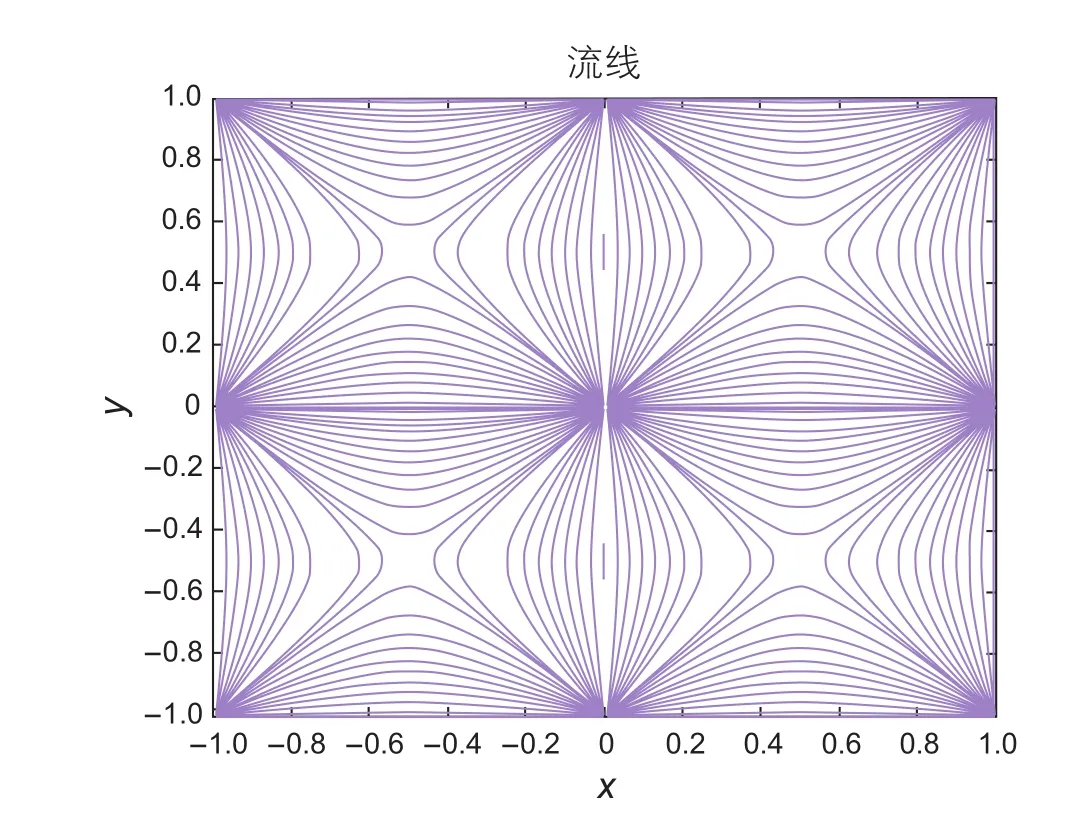
图6 流场分布(α=0.017 MPa-1)Fig. 6 Streamline distribution (α=0.017 MPa-1)

图7 流场分布(α=0.028 MPa-1)Fig. 7 Streamline distribution (α=0.028 MPa-1)

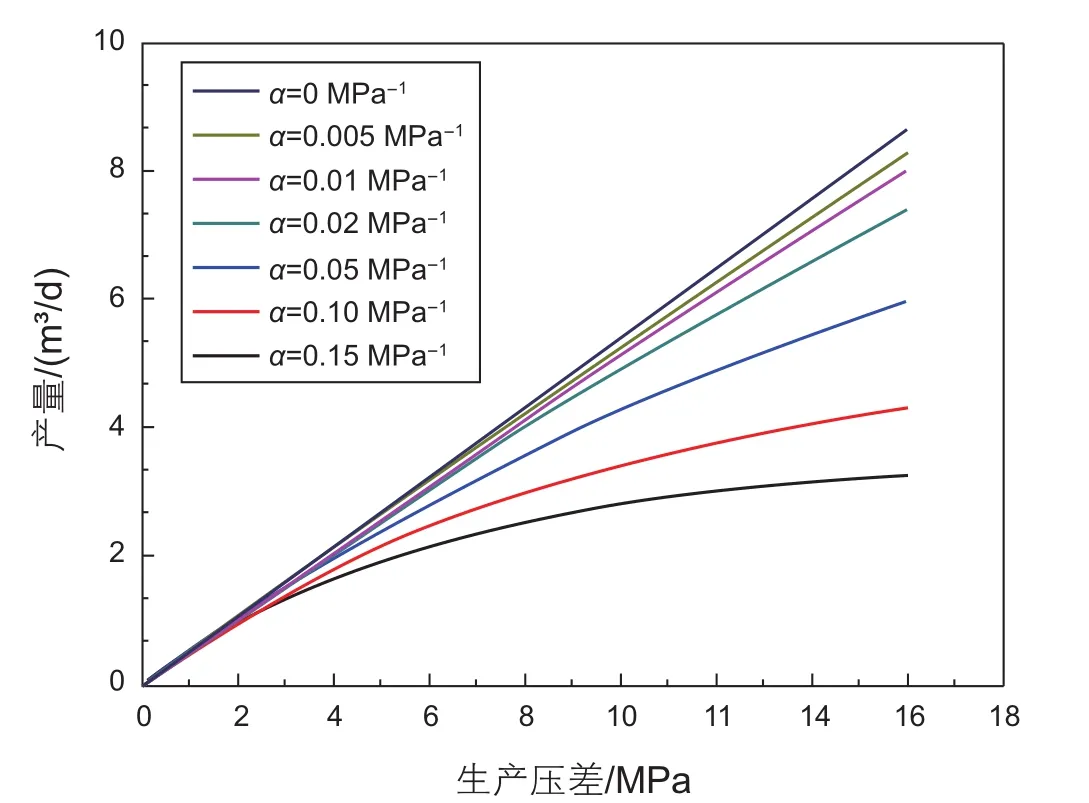
图8 产量与生产压差关系图Fig. 8 The graph of yield and production pressure drop

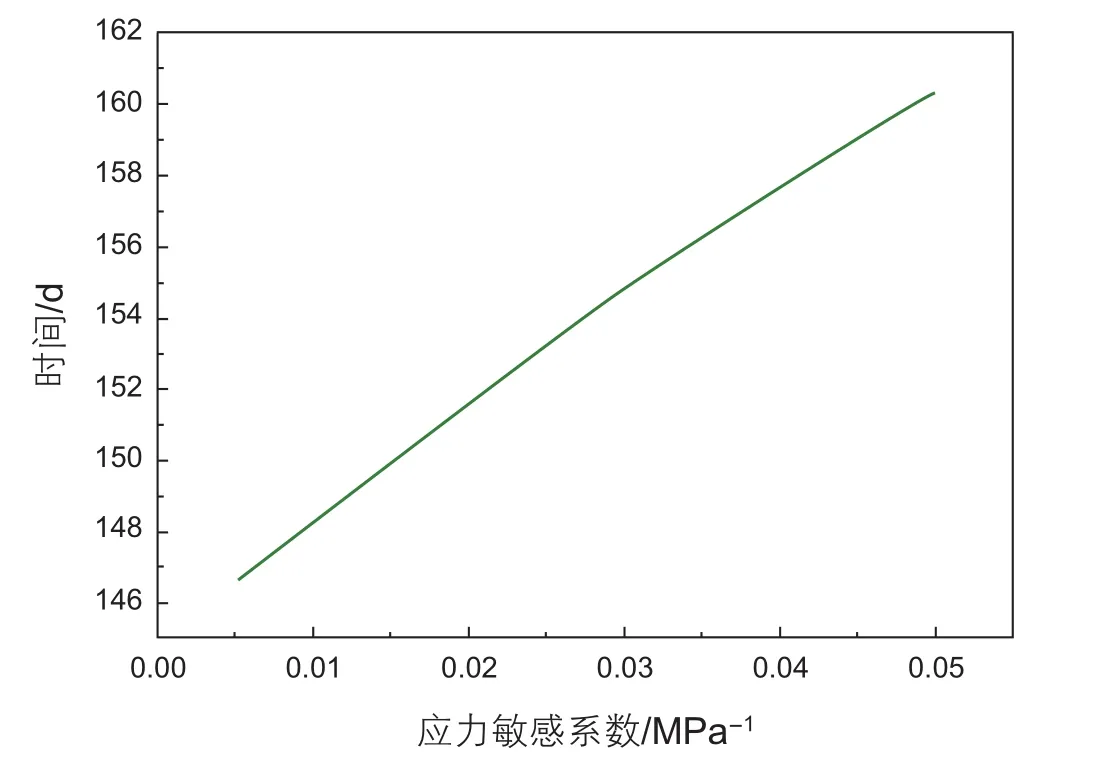
图9 见水时间与介质变形系数关系图Fig. 9 The breakthrough time and media deformation factor

3.4 介质变形系数对剩余油饱和度的影响

在不同介质变形系数下，通过式(17)计算生产50 d后地层剩余油饱和度分布，结果如图10和图11所示。由图10、图11可见，随着介质变形系数增大，地层剩余油饱和度增大，说明应力敏感效应不利于油藏生产，且应力敏感效应越强烈，油藏采出程度越低。

3.5 介质变形系数对水驱前缘的影响

在不同介质变形系数下，通过式(17)计算生产130 d后地层含水饱和度分布，结果如图12所示。由图12可见，随着介质变形系数增大，水驱前缘移动距离减小。在同一位置，含水饱和度随变形系数的增大而减小。说明应力介质变形对水驱效率有不利影响，岩石应力效应越强烈，水驱油效果越差。

图10 剩余油饱和度分布(α=0.028 MPa-1)Fig. 10 Remaining oil saturation distribution (α=0.028 MPa-1)

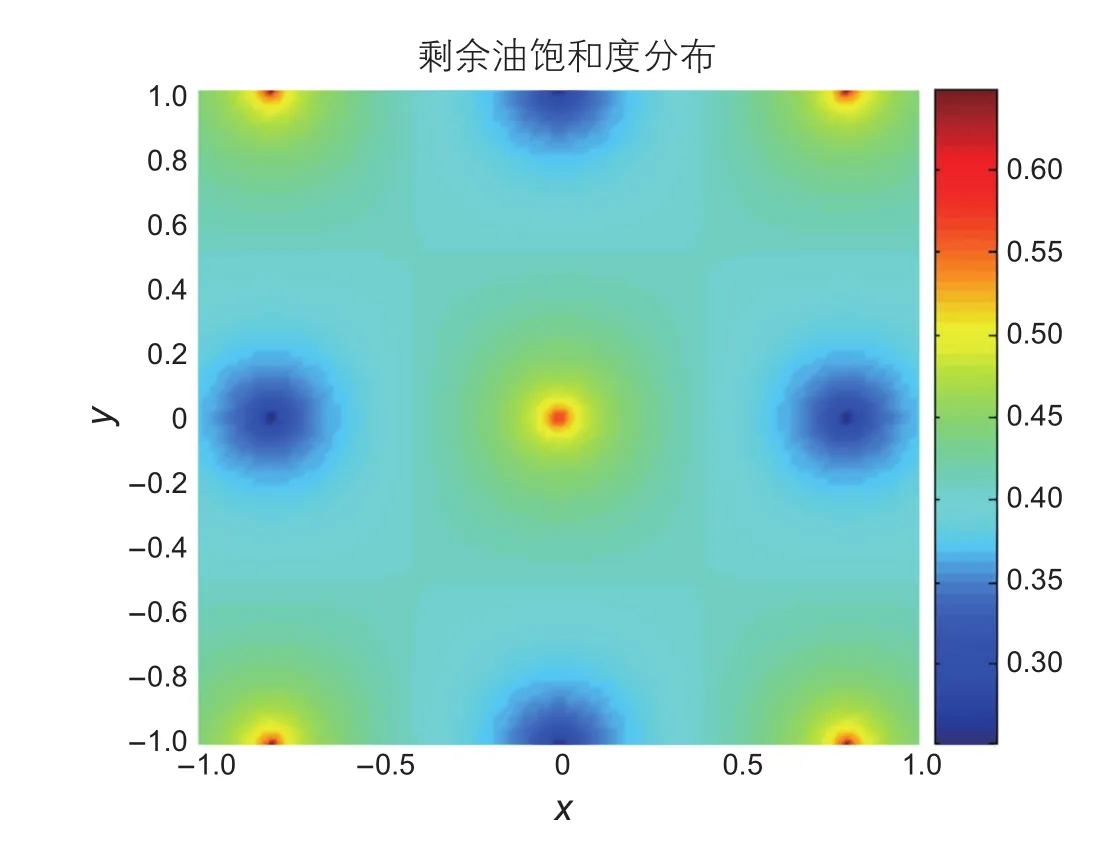
图11 剩余油饱和度分布(α=0.014 MPa-1)Fig. 11 Remaining oil saturation distribution (α=0.01 MPa-1)

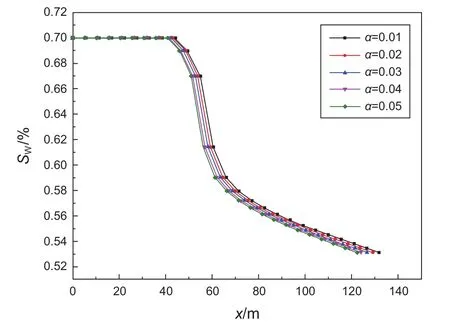
图12 含水饱和度与介质变形系数关系图Fig. 12 The water saturation with media deformation factor

4 结论

(1)基于油水两相渗流方程，结合介质变形方程，推导了考虑介质变形的五点面积井网压力、流函数解析公式。

(2)根据地层流场分布，得到油井见水时间，结合物质平衡理论，推导出无因次井网单元有效动用系数计算公式，进而可以定量计算低渗透介质变形油田五点面积井网的有效动用系数。理论计算见水时间与实际生产情况基本一致，相对误差为9.9 %，符合性较好，说明本文计算模型正确。根据油水两相渗流方程，得到了等饱和度面运动特征方程，进而可以得到地层剩余油饱和度分布。

(3)介质变形系数造成面积井网动用程度降低，油藏采出程度降低。随着介质变形系数增大，地层渗流阻力增大，渗流速度减小，从而导致流线波及面积减小、油井见水时间增长；同时，由于介质变形系数增大，生产阻力随生产压差的增大而增大，水驱前缘移动距离减小，进而对储层渗透率产生重大影响，使产量与生产压差的关系不再遵循达西定律，产量增幅变小。

符号注释：

式中：v—为流体渗流速度，m/d；k0—岩石初始渗透率，μm2；k(p)—地层压力为p时地层绝对渗透率，μm2；p—地层压力，MPa；p0—初始地层压力，MPa；kr—相对渗透率；μ—流体黏度，mPa·s；α—介质变形系数，1/MPa；q—源汇项，1/d；φ—地层孔隙度，%；S—流体饱和度，%；t—时间，d；U—无因次压力；λt—混合流体流度，μm2/(mPa·s)；▽—Laplace算子，表示内积；Q—油井产量，m3/d；C,C1,C2—常数；r—距离，m；h—油层厚度，m；ψ—拟势函数，m2/(d·MPa)；vt—混合流体速度，m/d；T—见水时间，d；A—井网单元面积；ω—积分变量；fw—Leverrett分流函数；下标：o—油相，w—水相；m—井排排数，n—油井或注入井井数，M—地层中任意点。