基于ADAMS的新一代水下生产系统功能舱深水悬垂下放仿真研究

贾晓丽，郭永豪，刘书海，王懿

1 中国石油大学(北京)机械与储运工程学院， 北京 102249

2 中国石油大学(北京)海洋工程研究院， 北京 102249

悬垂下放法是针对超深水环境和较大重量管汇的安装专门设计的一种快捷、简便的安装方法，适用水深范围3000 m以内，对提升能力和气候窗要求不高。Petrobras公司最早采用悬垂下放法成功将280 t和200 t的管汇安装在1845 m和1900 m水深的位置[1]。姚丽琳利用FLUENT和SESAM对悬垂下放过程船-缆一体耦合系统进行了时域耦合分析，发现下放过程中，缆索张力稳定，不会出现对缆索造成致命破坏的突变载荷[2]。张万里以MOSES对PIM下放管汇的入水阶段和下放阶段进行模拟，分析了风速、流速和波高等参数的敏感性，并提出了一套适用于深水下放安装数值模拟的非线性耦合时域分析方法[3]。Wang等人提出了一种非传统悬垂安装方法，并且对1500 m水深195 t管汇的安装进行了研究，采用FLUENT和SIMO软件分析得到了船舶运动时间历程、管汇响应及缆索张力[4]。李欣等人采用非线性时域耦合分析技术对管汇悬垂安装进行了研究，结果表明水上船舶的运动对缆索有显著影响，管汇的重心、浮心等位置对运动也有重要影响[5]。赵梦一等建立了PIM法下放的风险评估体系，得出悬垂运动是事故多发阶段，波浪影响绞车承载能力和安装绳最大张力的确定等结论[6]。Madduma 等对Dual Cap-X下放阶段进行模拟，研究了海流速度、重量和阻力系数的敏感性。分析发现海流速度会影响全局响应，并且流速增加会延长重物下放时间，而增加重量可以缩短这一时间[7]。

掌握功能舱悬垂下放过程的动力学特性对悬垂下放的成功实施具有非常重要的影响，对缆索进行动力学建模分析是悬垂下放法研究非常重要的一种手段。Niedzweeki和Thampi于1991年提出了一种多自由度的集中质量模型[8]。随后，Kamman和Huston利用集中质量法对固定长度和可变长度缆段的拖曳系统进行了仿真[9]。在缆索有限段法方面，Kamman采用三维有限段方法研究了缆索的水下运动，通过与实验数据对比证明了此方法的可行性[10]。Triantafyllou采用此法研究了下端自由、上端作缓慢运动的锚链运动特性[11]。丁昱对多刚体动力学在锚链系统研究中的应用作了初步尝试，分析了锚链系统的运动及动力特性，并计算了锚链的张力变化[12]。王延辉等根据Huston的多体力学理论以水下弹性缆索为研究对象，发展了缆索的多体有限段模型，提出弹性缆段模型，用于求解弹性缆索的动力学响应[13]。

本文采用多体理论针对功能舱下放过程进行多刚体动力学建模，使用多体动力学分析软件ADAMS进行仿真，并将安装船与下放功能舱纳入整个多体系统。ADAMS求解器采用拉格朗日方程方法，可快速建立系统动力学方程，并用自带求解器对系统进行静力学、运动学和动力学分析。本文采用ADAMS命令流语言编写模型，将模型参数化，在此基础上研究流体速度、功能舱重力和缆索长度等关键参数对功能舱下放过程动力学特性的影响。

1 模型建立

新一代水下生产系统是将传统海底平面分散布置的水下装备集成到深水功能舱，形成全水下立体空间布局的创新性完整方案。功能舱安装在深水数十兆帕高压和4 ℃以下的环境中，这使得传统安装方法，如钻杆下放法、吊机下放法不再适用。在深水条件下，由于下放缆索或钻杆的自身重量使其承重能力下降很快，导致这两种方法失效。另外，缆索和钻杆的长度增加也会加剧轴向共振[14]，而悬垂下放法可以避免此种情况的发生。以下放管汇为例，悬垂下放法流程如图1所示：在安装地点，下放缆索一端与管汇相连，一端与安装船相连。运输船用吊机将管汇吊起，行驶一段距离，然后下放管汇通过飞溅区(水平面以下50 m内)，见图1(a)；之后运输船释放管汇，管汇靠自身重力像摆钟一样垂放至接近海底。受拖曳力以及绳索和浮力模块的阻尼作用的影响，管汇不会来回做钟摆运动，见图1(b)。本文把悬垂下放阶段分为三个阶段，图1(b)中1位置是开始阶段，中间的2位置是悬垂阶段，3位置是稳定阶段。

1.1 绕流阻力

在仿真分析中，缆索和功能舱流体阻力的处理对整个系统有很大影响。海洋环境参数主要有风、浪、流三部分构成，本文中定义下放过程开始时缆索和下放重物在飞溅区以下，故忽略了缆索和下放重物受到风浪的影响，重点考虑水流速度及其方向的影响。缆索和功能舱相对于波浪尺度很小，根据小尺度结构物的Morison公式进行圆柱绕流阻力的计算[15]。

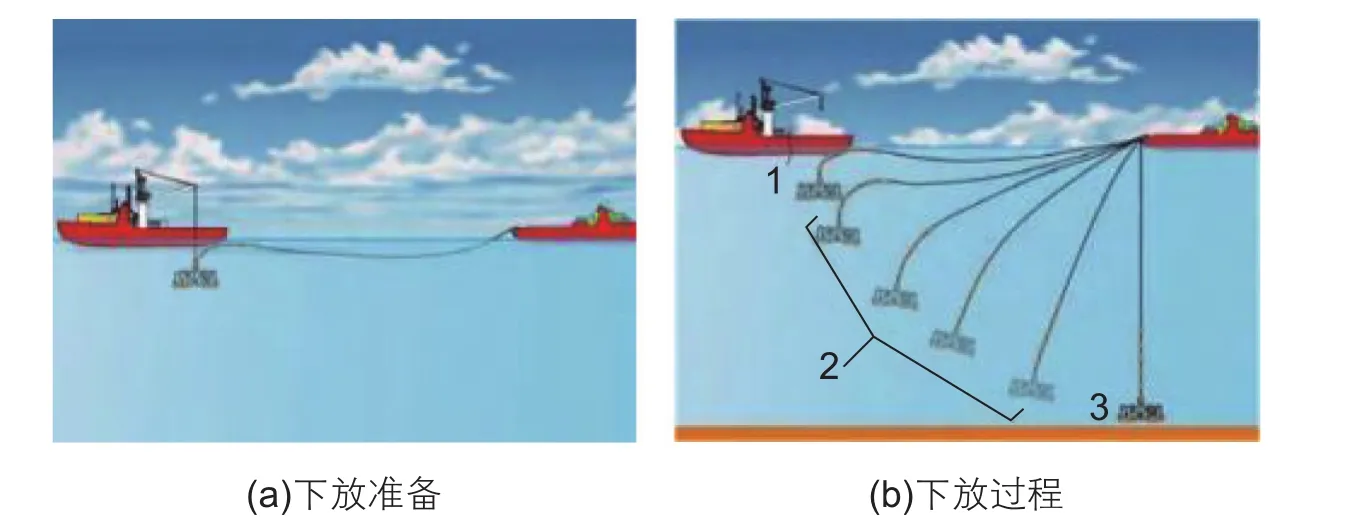
图1 悬垂下放流程示意图Fig. 1 Pendulous installation method flow diagram

根据Morison方程，绕流阻力由两项组成，如式(1)所示，第一项是与速度平方有关的拖曳力，第二项是与流体速度变化有关的惯性力。

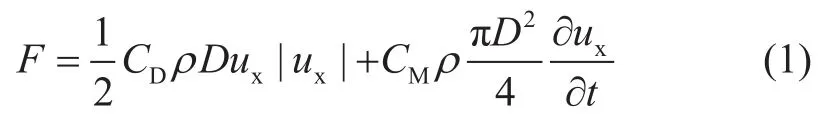
其中，CD、CM分别为拖曳力系数和惯性力系数，均无因次；ρ为流体密度，kg/m3；D为柱体直径，m；ux为流体相对速度，m/s。

为便于模型的建立，将式(1)中的拖曳力和惯性力分别向法向和切向分解，分解后的法向阻力如下

其中，CDn、CMn分别为法向拖曳力系数和法向惯性力系数，均无因次；un为相对流体法向速度，m/s。

分解后的切向阻力为

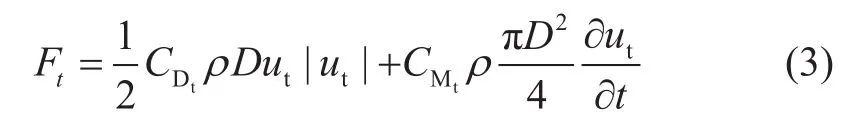
其中，CDt、CMt分别为切向拖曳力系数和切向惯性力系数，均无因次；ut为相对流体切向速度，m/s。

1.2 变阻力系数

大多数的缆索系统仿真中，都将阻力系数取为常数，对于平稳的动态过程这种取法基本满足要求。但是对于缆索曲率随时间变化较大的情况，阻力系数取常数是不准确的，因为曲率随时间变化大，意味着各点的速度差异很大，各点的雷诺数也就不同，导致阻力系数不同。因此，为了提高仿真精度，增强模型适应性，采用分段变阻力系数。根据李斯特实验[16]，取法向阻力系数为

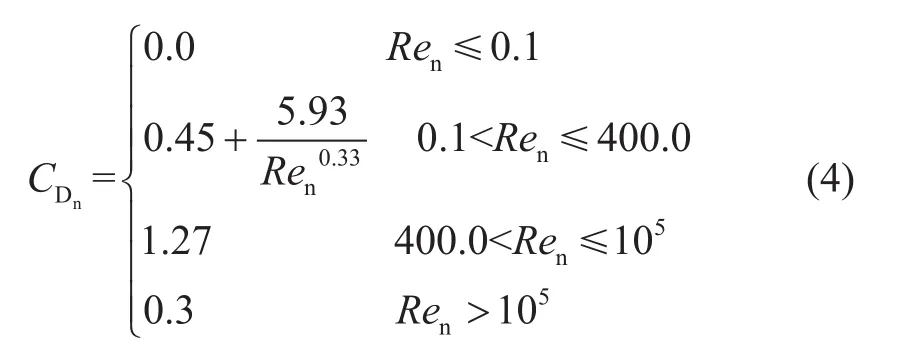
切向阻力系数为

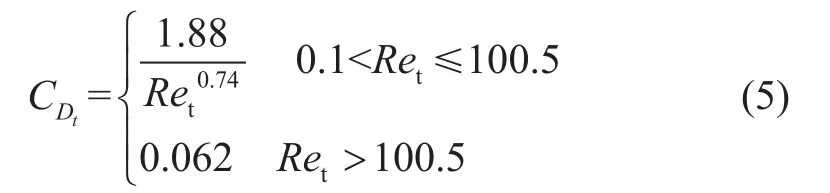
其中，Ren和Ret分别为法向雷诺数和切向雷诺数，均无因次。

1.3 仿真模型建立

缆索建模在ADAMS中有三种方法[17]：(1)多段小圆柱体加球铰链建模；(2)生成柔性体方式建模；(3)多段小圆柱体加轴套力方式建模。ADAMS中球铰链约束了两物体间的三个移动自由度，从提高仿真准确性角度可知多段小圆柱体加球铰链建模法不适用。对于大变形的柔性绳索类物体，生成柔性体方式无法直接建模。多段小圆柱体加轴套力的形式满足计算精度和计算速度的综合要求，易用命令流实现，并且它与缆索有限段模型相近，所以本文采用此方法对缆索进行建模。

悬垂下放法的缆索主要由三段组成：从安装船起，第一段为长度较短的链条，连接于安装船；第二段为长度较长的涤纶绳；第三段为布置了浮体单元的钢丝绳，整个模型见图2所示。其中(a)是模型的示意图，(b)是整体模型，(c)、(d)、(e)分别为几个连接处的局部放大图。图3是分布式浮力模块，它分布在钢丝绳上。

在ADAMS环境下，首先定义随物体移动的单向力，根据公式(2)、(3)添加每一段小圆柱体和功能舱的法向及切向绕流阻力。在ADAMS中，可以利用设计变量来定义下放系统的参数，利用状态变量来补充定义与时间有关的参数。利用设计时函数来获得指定物体对于给定坐标系的线(角)速度、线(角)加速度等运动学量，将获得的这些量定义成状态变量或者直接写入每一小段模型力的表达式中，就完成了模型中流体阻力的添加[18]。

其次定义固定在全局坐标系下的单向力，可以添加每一个小圆柱体、功能舱、分布式浮力模块的浮力。在模型中，每个浸入海水中的物体上均作用有浮力，浮力大小由该部分体积确定，体积可以由设计变量参数直接写出。重力默认Y方向，加速度大小为-9.80665 m/s2。浮力如式(6)所示：

其中，ρ为流体密度，kg/m3；g为重力加速度，m/s2；Dk为第k段物体的柱体直径，m。轴套力在ADAMS中只需给定六个方向的刚度和阻尼即可添加。此外，功能舱相比管汇来说，外形较简单，可将其简化为球体加圆柱体的组合体形式。

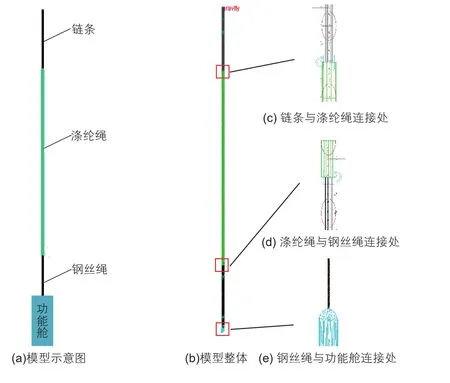
图2 模型示意图Fig. 2 Model diagram

图3 分布式浮力模块Fig. 3 Distributed buoyancy module

如上所述下放系统中每个物体所受的重力、浮力、弹性力、切向和法向流体阻力添加完毕，ADAMS将上述图形模型所有信息汇总后在后台编译成物理模型，然后利用刚体质心笛卡尔坐标和反映刚体方位的欧拉角作为广义坐标，利用带拉格朗日乘子的拉格朗日第一类方程的能量形式得到动力学方程，集成约束方程后ADAMS可自动建立系统的动力学方程，即微分代数方程。ADAMS自带多个求解器用于解决微分代数方程，对求解器进行设置后，即可求解上述数学模型文件，得到广义坐标的数值解。

需要注意的是，在ADAMS中建立缆索模型时需要将其离散成多段小圆柱体，而且链条的总长、各段半径等参数都是研究下放过程动力学特性的关键影响因素，这就需要分别建立不同参数的模型进行仿真分析。在这种情况下，如果手动建立模型将大大增加建模仿真时间，且容易出错，本文采用ADAMS提供的命令流进行建模在一定程度上解决了上述问题。

2 ADAMS模拟分析

2.1 模型验证

为了验证模型的有效性，以上述建模方法模拟管汇下放过程。下放过程的坐标系如图4(a)所示，以安装船与链条连接处为原点，以安装船与运输船连线方向为x轴，以垂直水面方向为y轴。缆索和管汇参数如表1、2所示[6]，设海洋水流速度为0.3 m/s，方向沿x轴水平向右，仿真得到的钢丝绳与管汇连接处张力时间历程如图5所示。

图4 模型坐标系Fig. 4 Model coordinate system

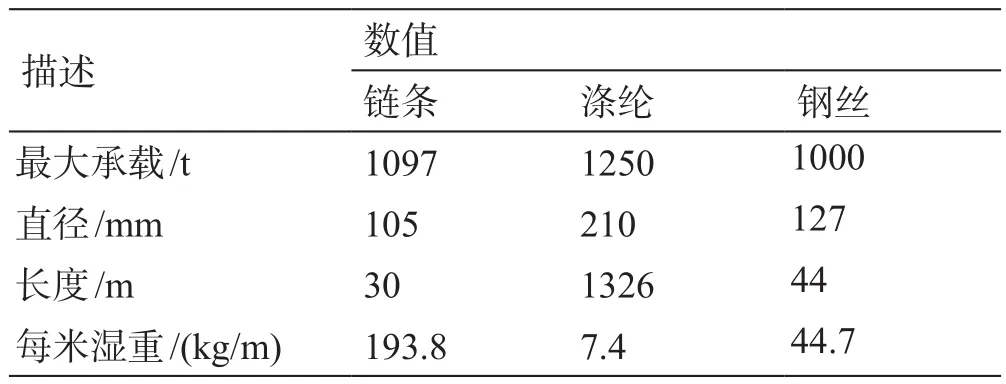
表1 缆索参数[6] Table 1 Cable parameters[6]

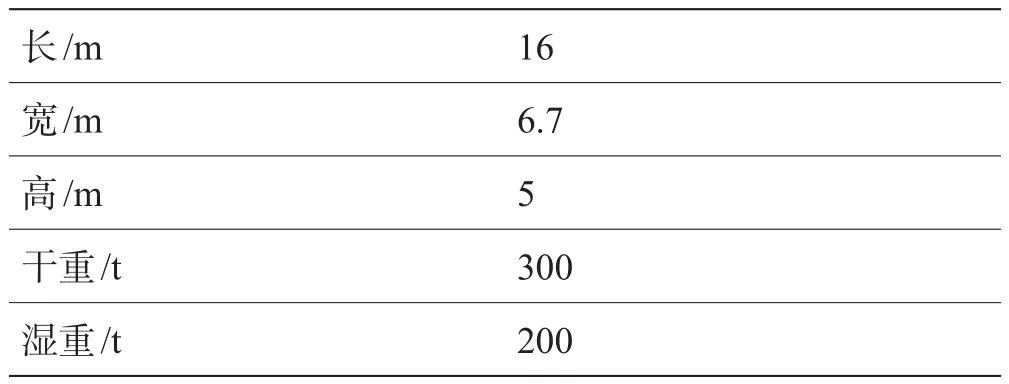
表2 管汇参数[6] Table 2 Manifold parameters[6]

由图5可知，本文仿真结果与参考文献[6]基本相符，钢丝绳与管汇连接处张力在开始200 s内本文仿真数据平均值是7.63×105N，参考文献数据平均值是7.70×105N，误差为0.91%。悬垂下放开始后260 s到500 s之间与文献稍有偏差，分析原因是本文没有考虑风浪对安装船的影响，且简化了安装船与海洋的受力关系，但本文仿真值基本高于参考文献结果，安全系数可以保证。在受力稳定的600 s到1200 s内，本文仿真数据平均值是2.02×106N，参考文献数据平均值是1.97×106N，误差为2.53%。

综上所述，本文建模方法可行，可以对功能舱的悬垂下放过程进行仿真。

2.2 功能舱悬垂下放仿真

与管汇下放相似，功能舱下放过程坐标系如图4(b)所示，功能舱悬垂下放仿真相关参数如表3所示，流体速度方向沿x轴水平向右。下放过程中功能舱位置x、y坐标变化如图6所示，安装船与链条、链条与涤纶绳、涤纶绳与钢丝绳、钢丝绳与功能舱四个连接处的张力时历见图7。

由图6可知，功能舱在250 s左右进入稳定阶段。从图7可以看出，安装船与链条连接处和链条与涤纶绳连接处的曲线在前20 s快速上升，之后缓慢下降，在50 s后又开始缓慢上升直到稳定。涤纶绳与钢丝连接处和钢丝绳与功能舱连接处曲线在前25 s快速上升，之后缓慢下降直到平稳。四个连接处达到的最大张力值分别为3.94×106N，3.88×106N，4.23×106N，4.51×106N，说明受力最危险的地方在钢丝绳与功能舱连接处，并且由图7知此四处张力在前25 s都存在明显波动。可以考虑在功能舱周围也布置浮式模块，增加阻尼以减小下放开始的波动。在选择缆索时可以把最大张力作为参考，选取具有合适承载能力的缆索。

2.3 关键参数影响分析

2.3.1 流体速度

流体速度分别取0.0 m/s、0.2 m/s、0.4 m/s、0.6 m/s、0.8 m/s，其它参数不变。图8～10为不同流体速度下钢丝绳与功能舱连接处张力时间历程、功能舱重心的x轴、y轴坐标时间历程曲线，各图中图(b)均为图(a)的局部放大图。由图8可知随着流速增加钢丝绳与功能舱连接处受力减小。图9表明流速分别取以上数值时功能舱的水平最大移动距离分别为1410.43 m、1406.70 m、1402.30 m、1399.15 m、1394.23 m，可知随着流体速度增加，功能舱受到阻力增加，最大水平移动距离变短。图9和图10可以看出，随着流体速度的增加，功能舱下放速度变慢。

图5 钢丝绳与管汇连接处张力时间历程Fig. 5 Tension time history of connection between wire rope and manifold

表3 仿真相关参数Table 3 Simulation related parameters

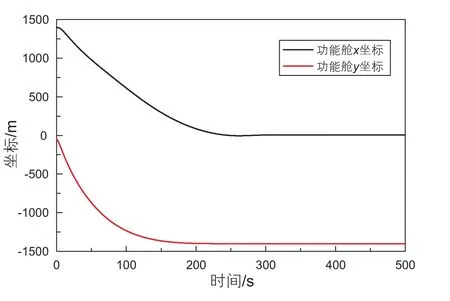
图6 功能舱x，y坐标时间历程Fig. 6 Function module x, y coordinate time history

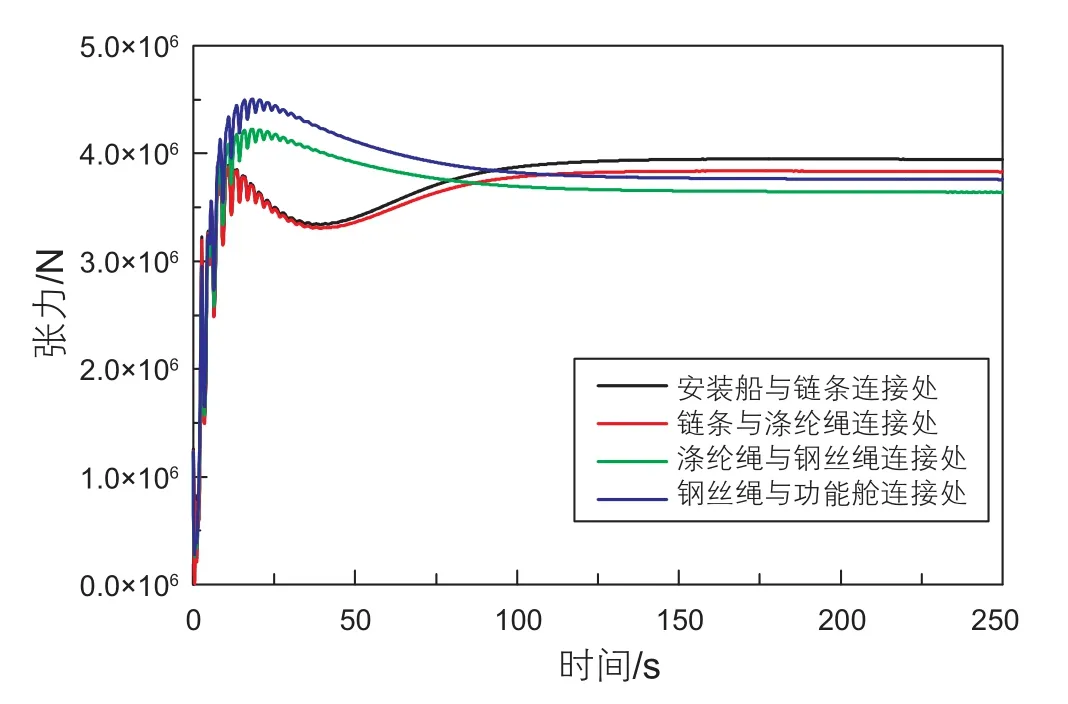
图7 四个连接处张力时间历程Fig. 7 Tension time history of four joints

2.3.2 功能舱重力

设功能舱重力分别取 469 t、528 t、586 t、645 t，其它参数不变。图11、图12为不同功能舱重力下钢丝绳与功能舱连接处张力时间历程、功能舱重心的x轴、y轴坐标时间历程曲线。由图11可知，随着功能舱重力的增加，钢丝绳与功能舱连接处受力明显增大。图12(a)中不同功能舱重力下的水平最大移动距离分别为1404.38 m、1406.50 m、1408.19 m、1409.70 m，说明随着功能舱重力增加，功能舱水平最大移动距离增大。由图12(a)、(b)可以看出随着功能舱重力增加，功能舱下落速度加快，从开始下放到接近平衡位置的时间缩短。

图8 不同流体速度下钢丝绳与功能舱连接处张力时间历程Fig. 8 Tension time history of connection between wire rope and function module under different fluid velocity

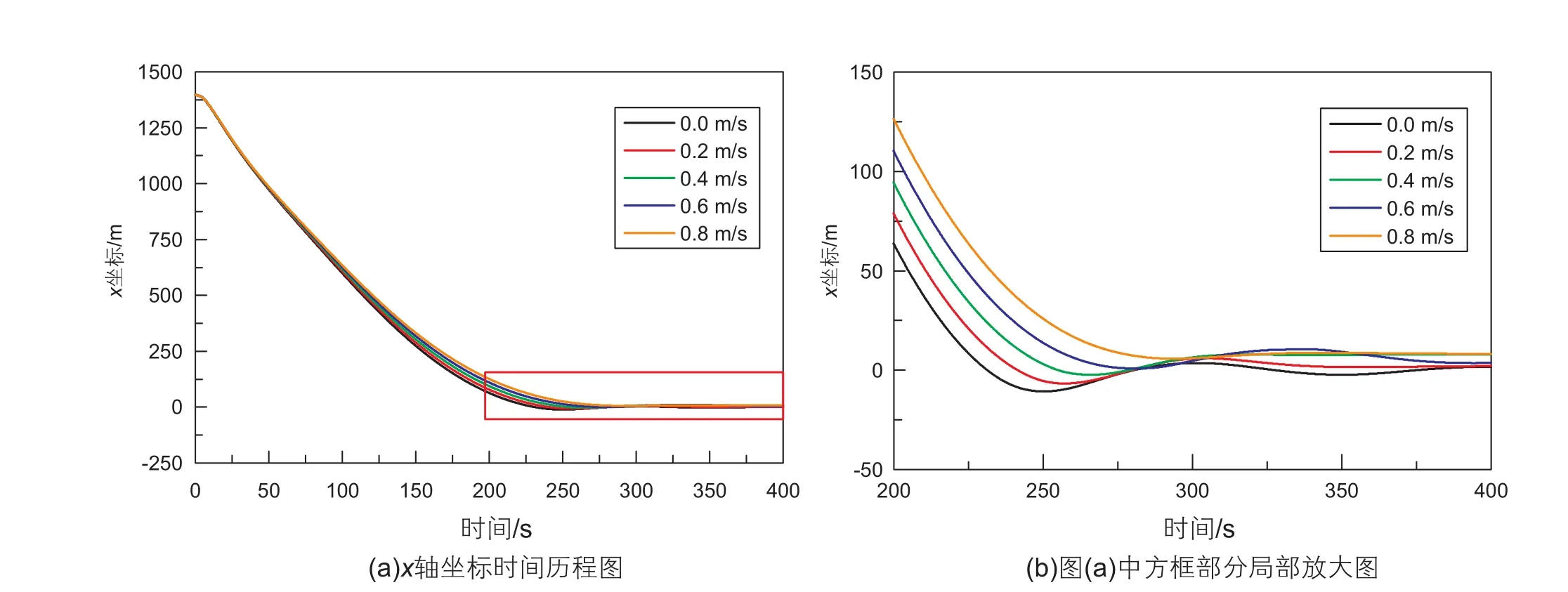
图9 不同流体速度下功能舱重心x轴坐标时间历程Fig. 9 x axis coordinate time history of the center of gravity of function module under different fluid velocity

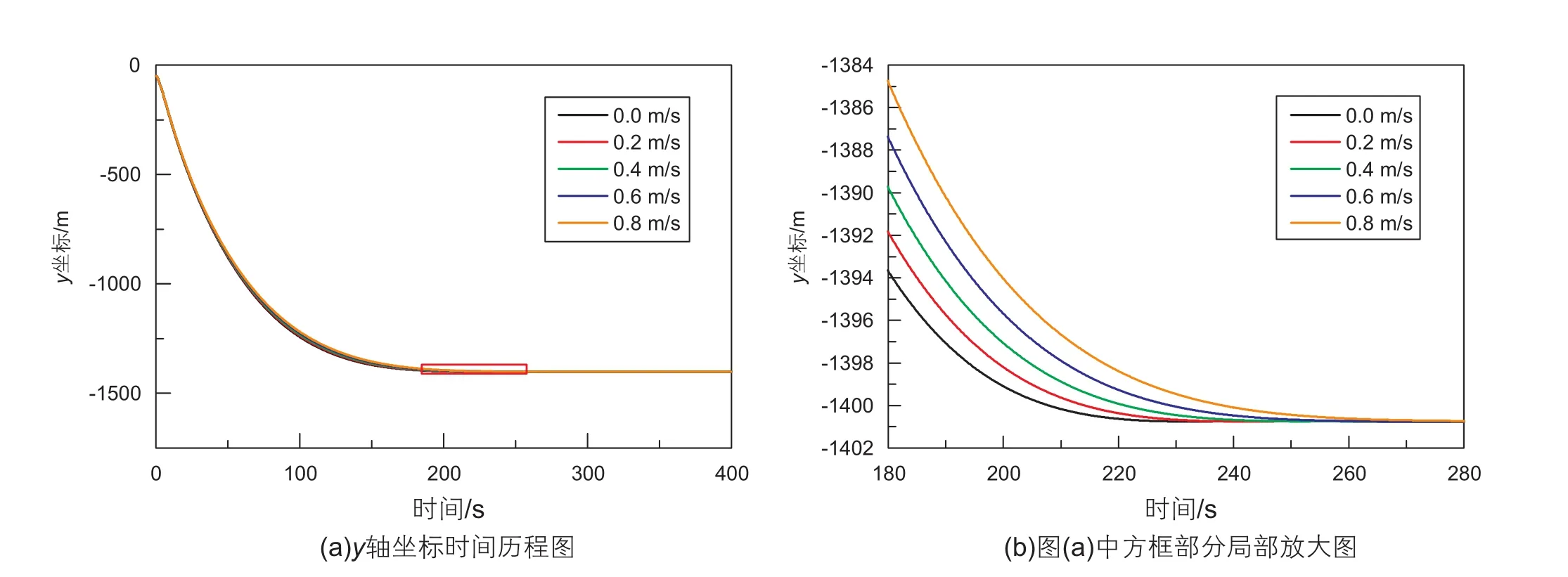
图10 不同流体速度下功能舱重心y轴坐标时间历程Fig. 10 y-axis coordinate time history of the center of gravity of function module under different fluid velocity

2.3.3 缆索总长

分别取缆索总长度为900 m、1200 m、1500 m、1800 m，即对应改变涤纶绳长度为826 m、1126 m、1426 m、1726 m，其它参数不变。图13、图14为不同缆索总长下钢丝绳与功能舱连接处张力时间历程、功能舱重心的x轴、y轴坐标时间历程曲线。由图13可知钢丝绳与功能舱连接处张力在前25 s迅速增大，之后缓慢下降直到平稳。在25 s到150 s左右，随着缆索长度增加，钢丝绳与功能舱连接处张力变化变慢。由图14可知，随着缆索长度增加，下放时间变长。

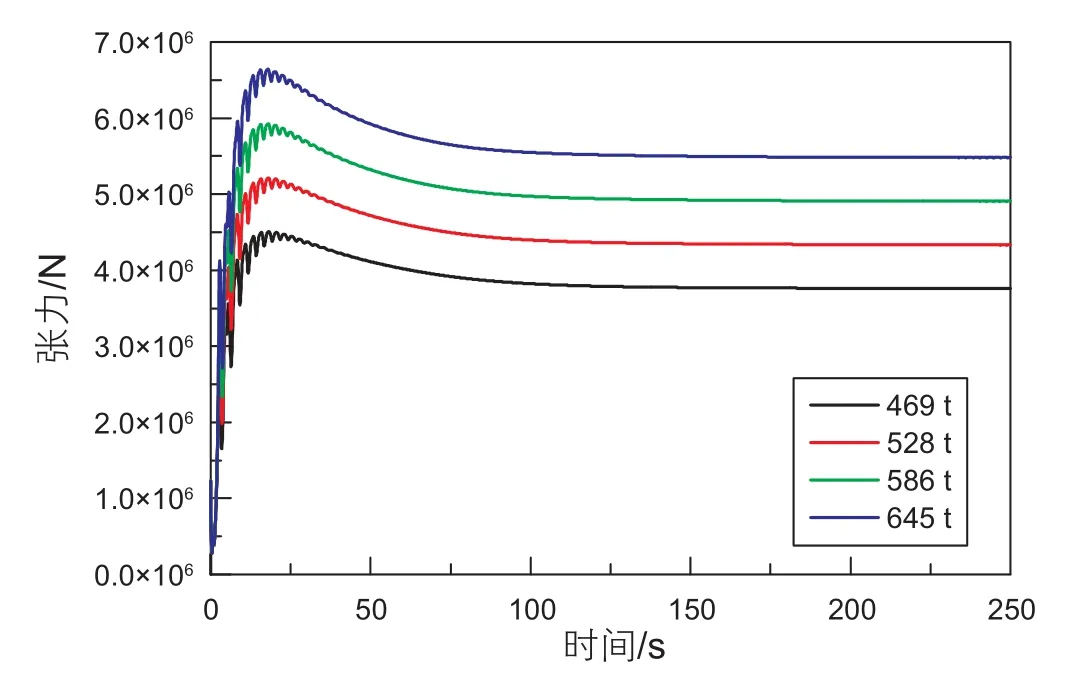
图11 不同功能舱重力下钢丝绳与功能舱连接处张力时间历程Fig. 11 Tension time history of connection between wire rope and function module under different weight of function module

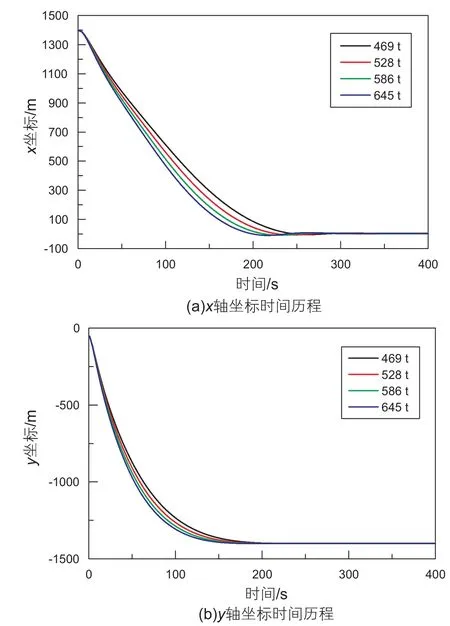
图12 不同功能舱重力下功能舱重心x，y轴坐标时间历程Fig. 12 x, y axis coordinate time history of the center of gravity of function module under different weight of function module

图13 不同缆索总长下钢丝绳与功能舱连接处受力时间历程Fig. 13 Tension time history of connection between wire rope and function module under different cable length

图14 不同缆索总长下功能舱重心x，y轴坐标时间历程Fig. 14 x, y axis coordinate time history of the center of gravity of function module under different cable length

3 结论

本文基于ADAMS对功能舱悬垂下放过程进行仿真，根据Morison公式进行绕流阻力计算，建立了悬垂下放多刚体动力学仿真模型，通过对比验证了模型有效性，并进一步讨论了流体速度、功能舱重力和缆索长度对下放过程的影响。研究发现：1)随着流速增加，钢丝绳与功能舱连接处张力变小，功能舱受到阻力增大，最大水平移动距离变短；2)随着功能舱重力增加，钢丝绳与功能舱连接处受力明显增大，功能舱水平最大移动距离增大，下落速度加快，接近平衡位置的时间缩短；3)随着缆索总长度增加，钢丝绳与功能舱连接处张力在激增后，缓慢下降，功能舱下放时间变长。本文仿真方法可以预测在不同流速下下放各阶段缆索承载力及下放功能舱的运动轨迹，可对新一代水下生产系统安装提供一定的理论指导。