时空变自适应反Q滤波

郭志伟，曹思远*，袁殿

1 中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

2 中国石油大学(北京)地球物理学院，北京 102249

3 北京亿华通科技股份有限公司，北京 100084

1 引言

目前，全球油气勘探呈现着明显的全面(常规和非常规)、多样(各种类型油气资源)、更深(深层和超深层)的特点[1]。随着地震勘探要求的日益提高，高分辨率的地震资料处理对后期的油藏描述和开发显得至关重要。地震波在地层介质传播过程中的吸收衰减是影响地震资料分辨率的主要原因，主要表现为振幅衰减、相位畸变、频率降低等特征[2]。地层介质的吸收衰减作用是造成地震波能量衰减的一个重要因素，频率越高，衰减越快，严重影响了地震资料的中深层成像能力和储层预测的精度[3]。反Q滤波是对吸收衰减进行有效补偿的方法，能较好地补偿振幅和校正相位，具有较准确的物理机制[4]。在反Q滤波的实现算法方面，不同学者进行了大量的研究[5-14]。Robinson[15-16]提出了频率域内插值的相位反Q滤波及其改进算法。Hale[17-18]根据Futterman模型提出了用泰勒级数展开近似高频补偿的反Q滤波。Bickel等[19]提出了基于复函数平面波的反Q滤波算法。McCarley[20]提出了基于自回归模型的常Q滤波方法。Varela等[21]提出了Hale反Q滤波算法的改进方法。裴江云等[22]通过麦克劳林级数展式推导了基于Kjartansson模型的高阶近似反Q滤波公式，其一阶近似式与Hale的反Q滤波式一致。Bano[23]将常Q模型相位反Q滤波拓展到层Q值模型。在补偿过程中，由于低信噪比和机器误差等因素，高频成分出现补偿溢出的现象。针对该缺点，人们提出了增益补偿函数，其作用是实现各频率振幅合理有效的补偿，通常在某个频率点之后逐渐减小补偿系数(即遵循低频充分补偿、中频欠补偿、高频不补偿的原则)。Wang[24-28]基于波场向下延拓提出了稳定高效的Gabor域反Q滤波，采用的增益函数只需一个控制参数(稳定因子法)，即可实现自适应的稳定补偿处理。李合群等[29]在对比不同增益控制方法的基础上，提出了选择性更灵活的补偿算子，取得了较好的补偿效果。张固澜等[30]针对固定增益函数容易造成深层资料高频补偿不足的缺点，提出了时变增益函数，较好地恢复地震有效频带内的能量。吴吉忠等[31]提出了一种基于等效Q值的反Q滤波算法，进行补偿高频能量耗散和相位畸变校正。SHI等[32]将增益限与稳定因子设为随时间和地层Q值连续变化的参数，提出变增益限的反Q滤波方法，该方法能够补偿深层能量衰减，提高分辨率。赵岩[33]提出了一种变稳定因子的反Q滤波方法，其中稳定因子是地震波的传播距离、地震记录的频率以及品质因子Q的函数。WEI等[34]引入整形正则矩阵来实现振幅补偿的稳定计算，利用增益控制因子和噪声压制系数来压制噪声，改进了稳定化反Q滤波方法。XUE等[35]提出一种自适应稳定的反Q滤波方法，该方法利用同步压缩变换对地震信号主频段有效成分进行重构，同时压制主频段外环境噪声，能有效地补偿振幅衰减，抑制环境噪声，提高地震资料分辨率。

由于反Q滤波处理过程中需要兼顾信噪比，一般情况下，地震资料的信噪比越高，则期望补偿越充分。稳定因子法中的增益函数只有一个控制参量，其值越大，对高频的补偿越充分。基于上述特点和处理目标，通过建立增益参数和信噪比的映射关系，对资料不同信噪比的区域进行不同程度的补偿处理，即自适应增益反Q滤波。

2 基本原理

2.1 反Q滤波

根据地层吸收衰减等价于偏移的思想，地表波场的向下延拓可以表示为：

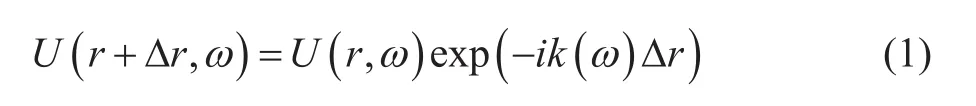
其中，U(r,ω)是角频率为ω传播距离为r的平面波波场，k(ω)代表波数，i是虚数单位。地震剖面图记录了从震源到反射点然后再回到地表的反射波。在波数的定义中引入地层品质因子Q：

v(ω)为与频率有关的相速度，将复波数k代入式(1)得：

用旅行时增量Δτ=Δ(ωr)代替距离增量，得到大地Q滤波的表达式：

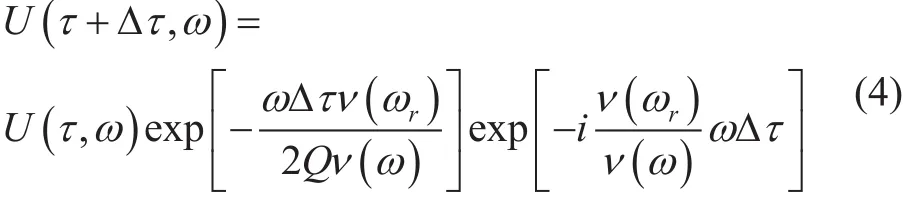
ν(ωr)参考频率ωr对应的相速度。根据Wang提出的改进的Kolsky频散模型，相速度ν(ω)近似为：

ωh为调谐频率，一般取值为地震带宽的最高频率，可以在反Q滤波时提供相对准确的相位校正。其中γ=(πQr)-1。注意：在频散式(5)中只考虑正频率，将之代入式(4)得：

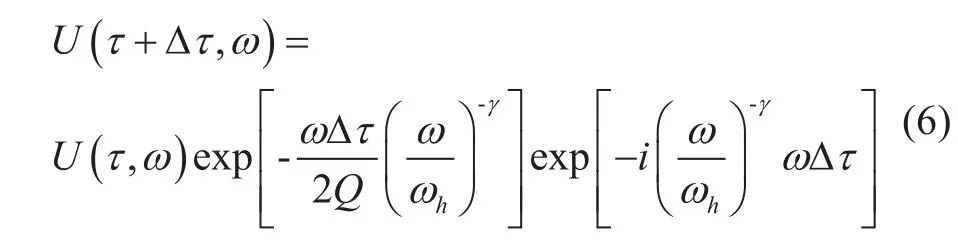
式(6)为基于波场延拓的Q滤波的基本公式，根据该式得到反Q滤波式：

式中有两个指数算子，前者为振幅补偿算子，后者为相位补偿算子。反Q滤波是在频率域进行的，最后对所有平面波求和得到补偿后的时间域地震信号：

2.2 自适应增益函数

直接对振幅进行补偿时会放大随机噪声与机器噪声，产生极大的不稳定性。为解决振幅补偿值溢出和高频噪音增大问题，采用稳定因子法构建增益函数。

衰减函数为β(τ,ω)：

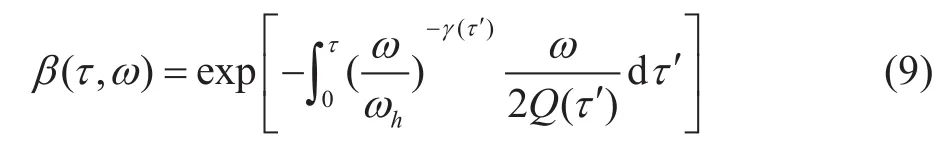
增益函数为Λ(τ,ω)：

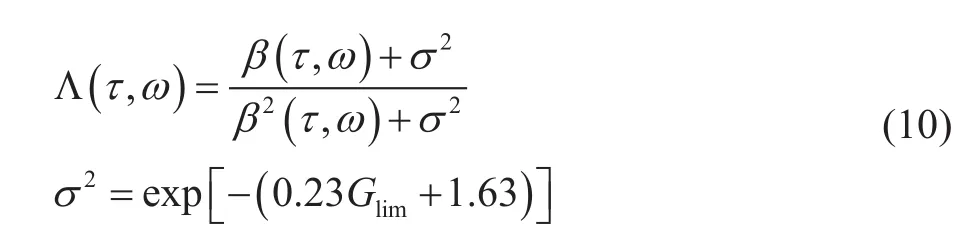
其中，σ2为稳定因子，Glim为增益参数(一般取10～100)，值越高，补偿越充分。根据式(10)，当ω非常大时，Λ(τ,ω)趋向于1，表明增益函数对该高频段不补偿也不压制。

我们接收到的地震记录一般包括有效地震反射波和各种各样的噪音，不同时刻的信噪比是不同的，即记录的信噪比是时间和空间的函数。以信噪比函数作为自适应增益参数的选取准则，建立Glim与信噪SNR(τ)之间的映射关系F，则有

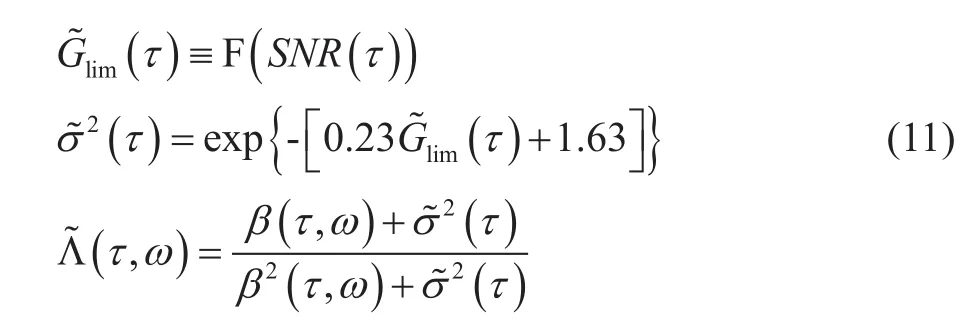
式中，稳定因子和增益参数与地震资料的信噪比有关，是时变参量，增益函数Λ~(τ,ω)具有自适应特征。当资料信噪比在时空域变化较大时，有必要采用式(11)来确定自适应稳定的增益参数进行反Q滤波。

映射关系F可根据信噪比SNR(τ)的实际特征设计，本文给出一种简单的线性定义：

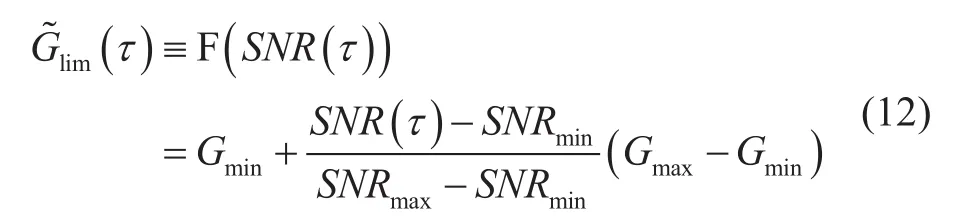
式中，待定参量Gmin、Gmax分别为最小和最大自适应增益参数，SNRmin、SNRmax分别为SNR(τ)的最小和最大值。

3 模型测试

3.1 无噪模型

设计5个反射系数界面的模型，反射系数值为1，分别位于 200 ms、350 ms、500 ms、650 ms和 800 ms，地面初始地震子波为50 Hz主频的Ricker子波，地下介质Q值为100。图1a是基于波场延拓正演的无噪衰减记录(不含几何扩散、反射/透射损失等固有衰减)，随着传播距离的增加，地震子波的延续长度逐渐增加、振幅衰减、相位改变。图1b是利用式(10)反Q滤波的结果，增益参数Glim取50。可以看到，在无噪情况下，中深层地震子波的波长、振幅和相位都得到较好的恢复和校正。图2是反Q滤波前(2a)、后(2b)时频谱的对比，吸收衰减降低了中深层记录的主频，反Q滤波较好地恢复了中深层记录的中高频成分。

3.2 含噪模型

对无噪模型添加不同程度的随机噪音，考虑在不同信噪比条件下，对比固定增益参数和自适应增益参数的反Q滤波效果。

图3a是含噪记录一，在无噪模型的基础上添加了0.75%的随机噪音，图3b是固定增益参数反Q滤波结果，图3c是自适应增益参数反Q滤波结果，其中，固定增益参数(见图4a)取30，自适应增益参数(见图4b)最大值取30，最小值取5。对比图3a和图3b，采用固定增益参数的反Q滤波较好地恢复了深层的弱反射信息(如800 ms处的同相轴)，同时扩大了随机噪音，大幅降低了信噪比水平；对比图3b和图3c，采用自适应增益参数的反Q滤波在恢复弱反射信息的同时，有效地控制了噪音的放大，深层的信噪比得到较好的改善。图5是反Q滤波前后的时频谱对比，图5a是原始含噪记录一的时频谱，图5b是固定增益参数反Q滤波记录的时频谱，图5c是自适应增益参数反Q滤波记录的时频谱。可以看到，固定增益参数的反Q滤波对噪音中高频成分的放大效果较为明显，自适应增益参数的反Q滤波则较好地控制了低信噪比区域的噪音(见红色圈中部分)，提高了时频谱的整体信噪比水平。

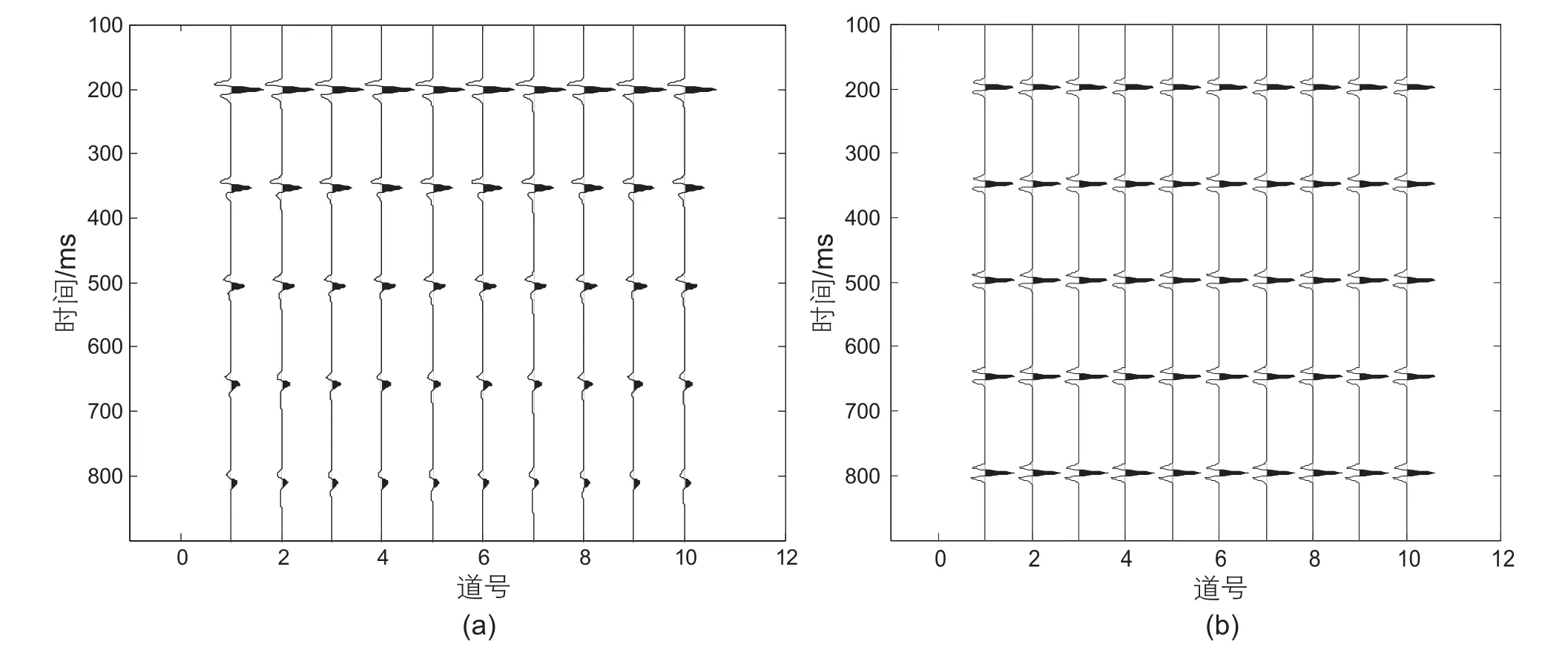
图1 无噪模型反Q滤波剖面对比(a)反Q滤波前；(b)反Q滤波后Fig. 1 Comparison of inverse Q filtering pro file of the noise-free model. (a)before inverse Q filtering; (b)after inverse Q filtering

图2 无噪模型反Q滤波时频谱对比(a)反Q滤波前；(b)反Q滤波后Fig. 2 Spectrum comparison of the noise-free model with inverse Q filtering. (a)before inverse Q filtering; (b)after inverse Q filtering

图6a是含噪记录二，在无噪模型的基础上添加了5%的随机噪音，图6b是固定增益参数反Q滤波结果，图6c是自适应增益参数反Q滤波结果，其中，固定增益参数(见图7a)取20，自适应增益参数(见图7b)最大值取20，最小值取1。图6a中的含噪记录，随着传播距离的增加，信噪比越来越低，500 ms和650 ms处的有效反射波较弱，同相轴信息不明显，800 ms处的反射信息淹没在随机噪音中，几乎看不到同相轴。图6b是采用固定增益参数的反Q滤波结果，与反Q滤波前剖面相比，信噪比进一步降低，500 ms和650 ms处的反射信息淹没在随机噪音中，分辨能力还不如反Q滤波前的剖面。图6c是采用自适应增益参数的反Q滤波结果，500 ms和650 ms处的反射信息得到较好的增强，信噪比得到较好的控制，800 ms处的弱反射同相轴得到一定的恢复，分辨能力得到一定的改善。图8是反Q滤波前后的时频谱对比，图8a是原始含噪记录二的时频谱，图8b是固定增益参数反Q滤波记录的时频谱，图8c是自适应增益参数反Q滤波记录的时频谱。在原始含噪记录的时频谱中(图8a)，650 ms以下的随机噪音与反射波的能量在同一量级；如果采用固定增益参数进行反Q滤波，对噪音的增强效果大于对有效反射波的恢复效果(图8b中红圈)，导致剖面中(图6b)500 ms以下的同相轴淹没在随机噪音中，不可分辨；如果采用自适应增益参数进行反Q滤波，650 ms和800 ms处的有效反射振幅得到较好的恢复，有效反射的能量团在时频谱中仍然占主要成分(图8c红圈)，清晰可辨。

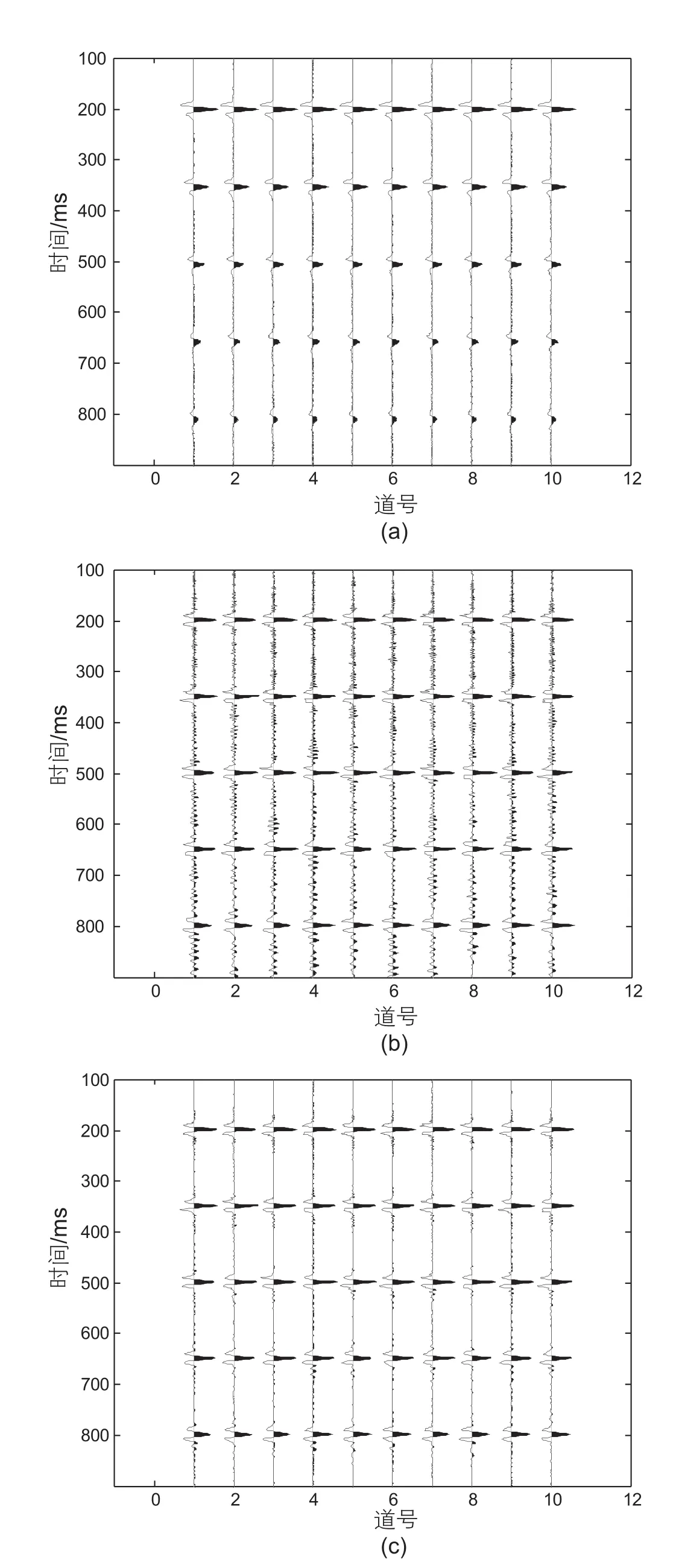
图3 含噪模型一(0.75%随机噪音)反Q滤波剖面对比(a)原始含噪记录；(b)固定增益反Q滤波；(c)自适应增益反Q滤波Fig. 3 Comparison of inverse Qfiltering profile in noise model 1 (0.75% random noise) (a)original noise recording; (b)fixed gain inverse Qfiltering; (c)adaptive gain inverse Qfiltering

图4 模型一增益参数(a)固定增益参数；(b)自适应增益参数Fig. 4 Model 1 gain parameter (a)fixed gain parameter; (b)adaptive gain parameter

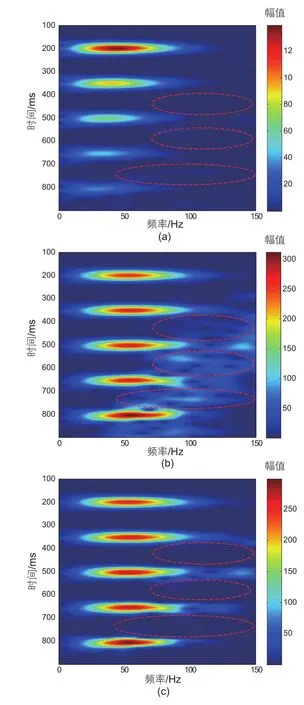
图5 含噪模型一(0.75%随机噪音)反Q滤波时频谱对比(a)原始含噪记录；(b)固定增益反Q滤波；(c)自适应增益反Q滤波Fig. 5 Spectrum comparison of inverse Qfiltering with noise model 1 (0.75% random noise) (a)original noise records;(b)fixed gain inverse Q filtering; (c)adaptive gain inverse Qfiltering

图6 含噪模型二(5%随机噪音)反Q滤波剖面对比(a)原始含噪记录；(b)固定增益反Q滤波；(c)自适应增益反Q滤波Fig. 6 Comparison of inverse Q filtering profile of noise model 2 (5% random noise) (a)original noise records; (b)fixed gain inverse Qfiltering; (c)adaptive gain inverse Qfiltering

图7 模型二增益参数((a)固定增益参数；(b)自适应增益参数)Fig. 7 Model 2 gain parameter ((a)fixed gain parameter; (b)adaptive gain parameter)

图8 含噪模型二(5%随机噪音)反Q滤波时频谱对比(a)原始含噪记录；(b)固定增益反Q滤波；(c)自适应增益反Q滤波Fig. 8 Spectrum comparison of inverse Qfiltering with noise model 2 (5% random noise) (a)original noise records; (b)fixed gain inverse Qfiltering; (c)adaptive gain inverse Qfiltering

4 资料处理

实际资料来自于沙漠工区，由于近地表吸收衰减严重，导致记录的主频较低(约为15～20 Hz)，严重影响了中深层的成像精度。图9a是原始叠加剖面，目的层4 s附近，图9b是采用固定增益参数的反Q滤波结果，图9c是采用自适应增益参数的反Q滤波结果，图9d是图9b与图9c所示的剖面之差。图10为固定增益参数与自适应增益参数对比，其中，固定增益参数为40(图10a)；自适应增益参数(图10b)最小值为10，最大值为60，主要分布范围在25～45。对比图9a、图9b和图9c，反Q滤波后剖面的同相轴变细，垂向分辨率得到提高(见黑色箭头)；对比图9b和图9c，两个剖面的分辨率相近，但图9c的信噪比高于图9b(如黑圈部分)，图9d显示了两者之差，主要是凌乱的反射和随机噪音，如果把这部分信息加到图9c中，则只会降低资料的信噪比，而对分辨率的提升却有限，这表明采用自适应增益参数的反Q滤波能较好地控制低信噪比区域的噪音扩大，有效改善反Q滤波剖面的信噪比。

图11是叠加记录反Q滤波前后的时频谱对比，图11a是原始叠加记录的时频谱，图11b是固定增益参数反Q滤波记录的时频谱，图11c是自适应增益参数反Q滤波记录的时频谱。对比发现，反Q滤波前叠加记录的时频谱(图11a)能量主要分布在10～30 Hz，经反Q滤波处理后，时频谱(图11b和图11c)能量主要集中在15～40 Hz之间，中高频成分得到较好的恢复；图11c的高频成分比图11b弱，这是由于该段记录的信噪比相对较低，采用了较小的增益参数(小于固定增益参数40)进行反Q滤波。值得注意的是，在图11b中，4000 ms处的主频(约为40 Hz)明显高于4500 ms处的主频(约为32 Hz)，在图11c中，4000 ms和4500 ms处的主频基本一致(约为30 Hz)，这说明自适应增益参数能较好地调节不同信噪比区域的补偿效果。

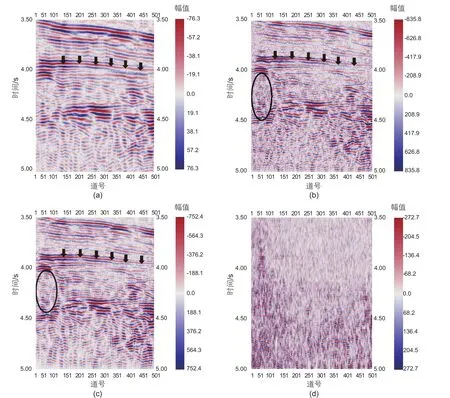
图9 叠后资料反Q滤波剖面对比(a)原始叠加记录；(b)固定增益反Q滤波；(c)自适应增益反Q滤波；(d)剖面b与剖面c之差Fig. 9 Comparison of inverse Qfiltering profile of post-stack data (a)original overlay records; (b)fixed gain inverse Qfiltering;(c)adaptive gain inverse Qfiltering; (d)the difference between section b and section c

5 结论

稳定的反Q滤波处理为了兼顾分辨率和信噪比，需要不断调试增益参数，将原始资料的信噪比作为先验信息，用于约束增益参数的选取，可实现地震资料自适应的反Q滤波处理。采用自适应增益参数的反Q滤波，根据资料不同区域的信噪比水平，能自动调节补偿效果，有效控制低信噪比区域的补偿，避免噪音被过度放大。需要注意的是，为避免反Q滤波剖面的突变，自适应增益参数应进行适当的二维平滑处理。

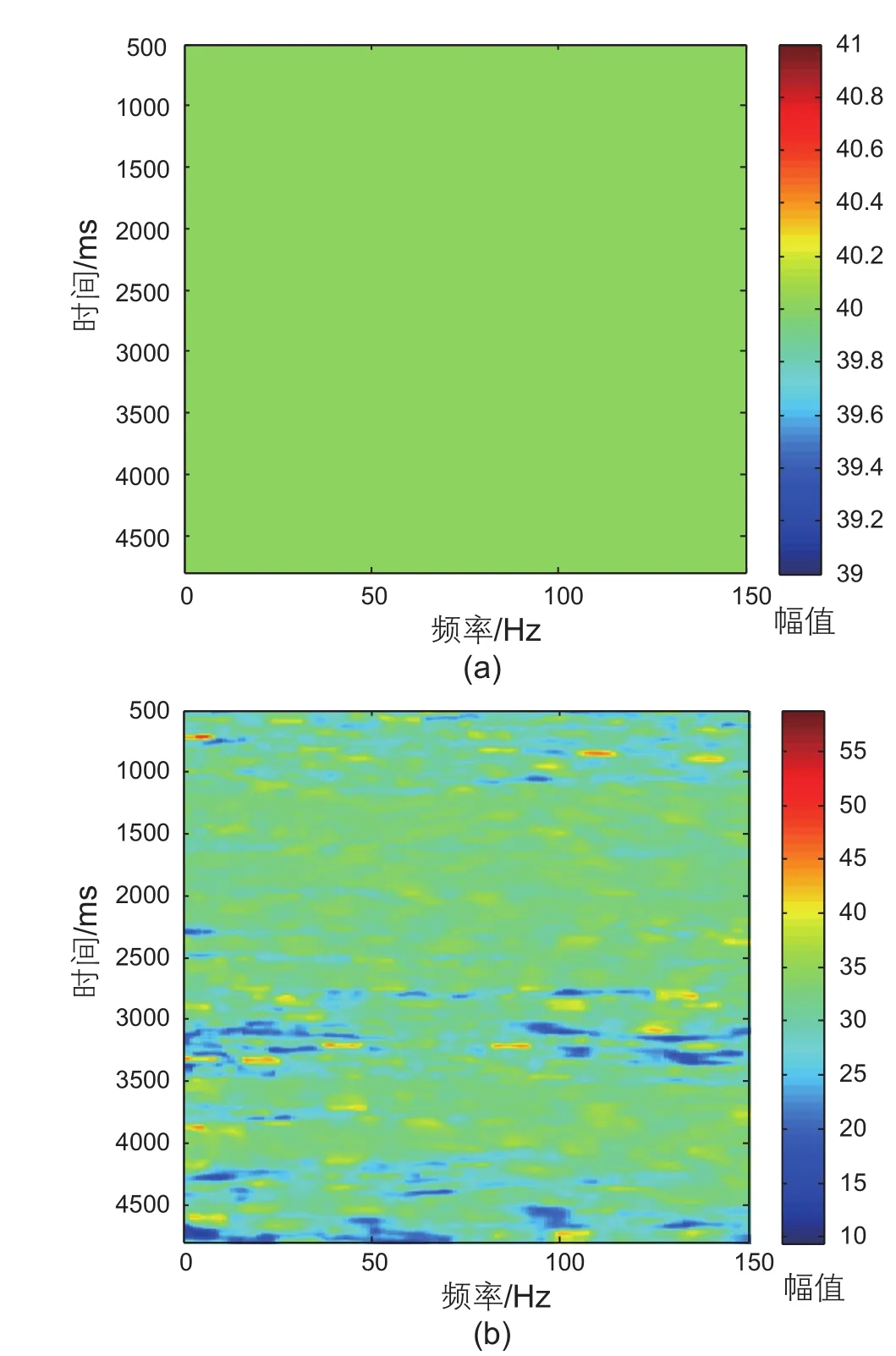
图10 实际资料增益参数。(a)固定增益；(b)自适应增益Fig. 10 Actual data gain parameter. (a)fixed gain; (b)adaptive gain

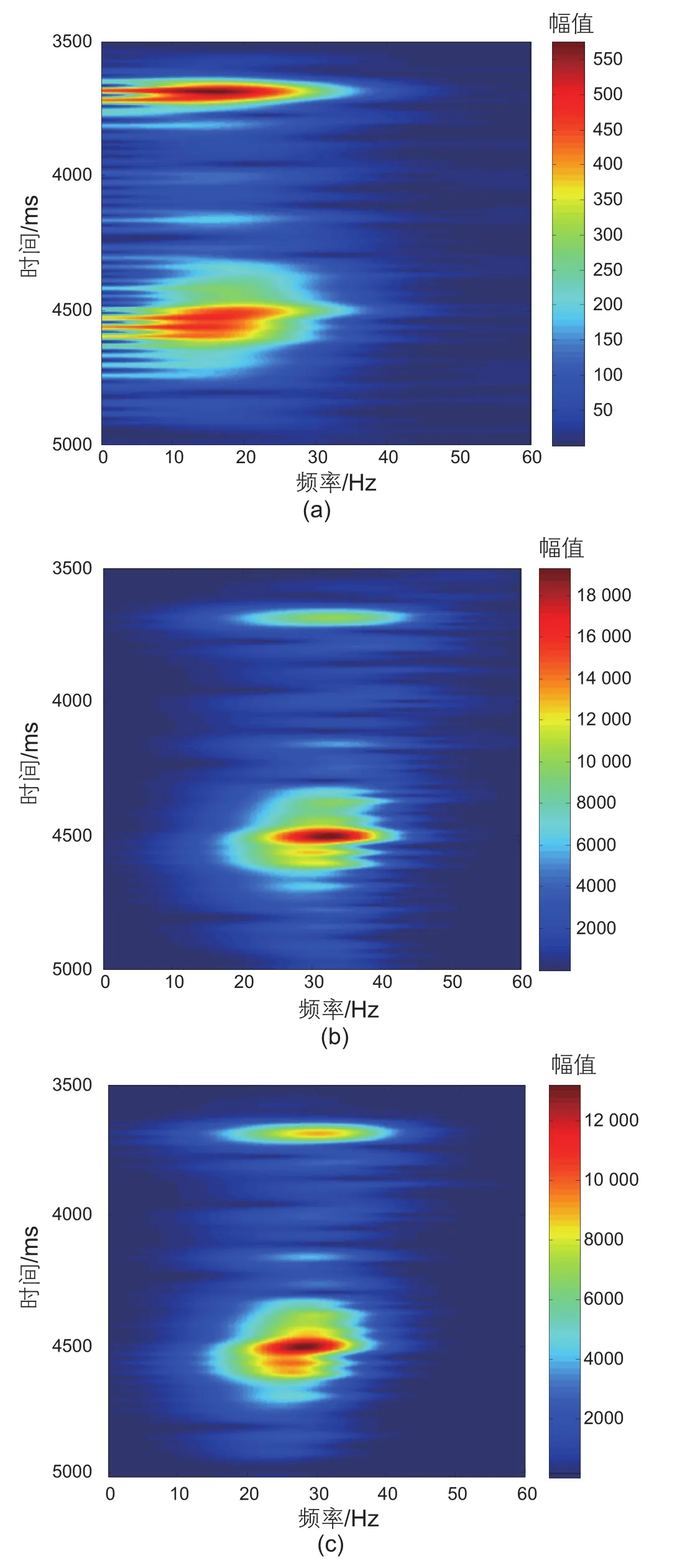
图11 叠加记录反Q滤波时频谱对比。(a)原始叠加记录；(b)固定增益反Q滤波；(c)自适应增益反Q滤波Fig. 11 Spectrum comparison inverse Qfiltering is recorded in superposition records. (a)original superposition records;(b)fixed gain inverse Q filtering; (c)adaptive gain inverse Qfiltering