低频地震岩石物理测量系统改进及致密砂岩实验研究

赵立明，唐跟阳，王尚旭，董春晖，贺艳晓，赵建国，孙超，韩旭

中国石油大学(北京)油气资源与探测国家重点实验室，北京 102249

0 引言

地震岩石物理实验能够建立地震响应与储层性质之间沟通联系的桥梁，在储层及流体预测中发挥着重要的作用[1-2]。常规岩石物理实验是在超声频段进行的，主要频段为0.1～1 MHz，超声测量数据由于频散效应可能大于地震频段测量数据[3-12]，超声数据直接利用或简单外插应用到实际地震勘探中，极可能造成地震数据误解释。为使岩石物理实验测量成果更好地指导油气勘探与开发，有必要在地震频段进行低频岩石物理弹性参数测量。Spencer首先利用应力应变振荡方法研发了地震频段岩石弹性参数测量系统，观测到4～400 Hz频段内饱和流体砂岩中随频率变化的杨氏模量及相关衰减[13]。应力应变振荡方法指的是对实验样品施加某一模式的周期性应力，实验样品受迫运动产生应变，通过应力应变(幅值、相位)计算相应模式的弹性参数及其衰减，如杨氏模量及其衰减、体积模量及其衰减等[14]。随后，Batzle等、Tisato和Madonna、Mikhaltsevitch等以及Pimienta等基于应力应变振荡方法各自构建了低频岩石物理测量系统，开展了一系列的低频岩石物理实验，对地震频段弹性参数的频散与衰减进行了深入的研究[15-20]。

中国石油大学(北京)低频岩石物理实验室在Batzle等设备基础上构建了低频地震岩石物理测量系统，并取得了一系列的实验成果[21-24]。未睍等在2～100 Hz频段范围内研究了孔隙流体对不同渗透率岩石地震波速度的影响[21]。Yin等在地震频段2～200 Hz内实验研究了流体黏度对致密砂岩弹性性质的影响，论证了喷射流是致密砂岩在地震频段频散与衰减的主导机制[22]。Sun等研究了影响低频地震岩石物理测量系统共振的因素，延后一阶共振频率，将系统的测量频段拓展为2～2000 Hz[23]。上述研究者实验时的最低频率为2 Hz，是由于现有系统采用过大的激振器(震源)应力补偿函数，使得激振器在频率2～5 Hz时输出应力过大，造成测量频段难以向更低频率的拓展，同时严重影响激振器的使用时限。此外，现有系统采用快速傅里叶算法(FFT)采集应变信号[22]，应变信号的准确采集实验周期过长，不利于低频测量在同一实验条件下进行，因此，现有系统需要一种高效数据采集方法。

基于上述问题，本文对实验室的低频地震岩石物理测量系统激振器补偿函数和应变信号采集方法进行了改进。为了检验改进效果，选取标准样品(铝和有机玻璃)对改进后的系统进行标定。在验证改进后系统的可靠性后，选取致密砂岩开展了低频弹性参数测量，并将低频测量结果与基于微观孔隙结构特征的喷射流模型模拟数据进行了对比分析。

1 低频地震岩石物理测量系统改进

1.1 低频地震岩石物理测量系统

低频地震岩石物理测量系统如图1所示，它主要由4个部分组成：低频测量装置、流体驱替装置、加温装置和围压加载装置。

低频测量装置的基本原理如下[15,21-24]：计算机程序控制函数发生器产生特定频率的电信号，电信号经功率放大器放大后，通过激振器将电信号转换为特定频率的正弦振动，两块标准铝样和岩样受迫振动，标准铝样及岩样上的应变片记录相应的应变大小(＜10-6)。应变信号经过电桥以电信号的形式输出，经信号放大器放大，由模数转换器将模拟信号转化为数字信号，计算机程序采集存储应变信号振幅相位信息。假设施加应力在标准铝样和岩样上分布一致的条件下，岩样的杨氏模量及泊松比由以下公式计算：

图1 低频地震岩石物理测量系统简图Fig. 1 Schematic view of low-frequency seismic rock physics measurement system

其中，EAl为已知的标准铝样杨氏模量，εAl、和分别为标准铝样纵向、岩样纵向及横向的应变信号振幅。

在岩样各向同性及均匀的情况下，由测量的杨氏模量及泊松比可以获取岩样的体积模量K、剪切模量μ、纵波速度VP及横波速度VS:

其中，ρSam为岩样密度。

低频测量实验在高温高压釜中进行，加温装置和围压加载装置可以提供储层温压条件。有效加载温度范围为-30 °C～120 °C，围压加载装置选用氮气作为围压介质，通过加压泵可加至70 MPa。流体驱替装置可以实现岩样饱和不同的流体或同一流体不同饱和度。

1.2 系统改进

在低频地震岩石物理测量系统中，激振器将特定频率的电信号转化为正弦运动产生应力，对激振器的控制来自于程序控制软件(LabVIEW)。为了能够精确生成振幅一定的正弦应力信号函数，避免造成激振器产生的应力振幅过小或过大而不满足应变测量的要求，程序控制软件需要选择合适的激振器应力增益补偿函数；另一方面，标准铝样和样品上采集的弱应变信号受随机噪音的干扰而信噪比降低，为了保证弱应变信号准确高效采集，弱应变信号的采集方法同样亟需改进。

1.2.1 优化激振器应力增益补偿函数

激振器的工作原理为通电导体在磁场中切割磁感线而受力运动，不同频率的交流电通过导体时，导体在磁场中做相应频率的正弦运动。在输入功率及载荷一定的情况下，激振器的应力输出函数随频率的变化如图2所示：在小于5 Hz时，由于激振器的机械性，其输出应力大小随着频率的增加以一定斜率直线增加；5 Hz以后，激振器的机械性能变得稳定，输出应力不再随频率发生变化。为了补偿激振器在频率较小时的低应力幅值输出，原有程序进行了增益补偿(即增加输入功率)，原有增益函数见图3a。图3b展示了激振器上加载原有增益函数后的应力实际测量结果(由标准铝样杨氏模量及其应变获得，已归一化)，从图中可以看出，原有增益函数加载过大，导致5 Hz前的应力输出大于激振器稳定后的应力输出。高应力输出一方面背离统一应力输出的初衷；另一方面，增益函数过大，使得输入功率激增，测量频段难以向更低频率的拓展。为了使测量频段内应力输出稳定，需优化原有的增益补偿函数。使用新的增益补偿函数后(图3a)，激振器的实际应力输出如图3b所示，新增益补偿后的应变输出以近直线的形式变化，更符合实际变化情况。在此基础上，同时考虑实验测量时间，将测量频段拓展到1 Hz，即测量频段拓展为1～2000 Hz。

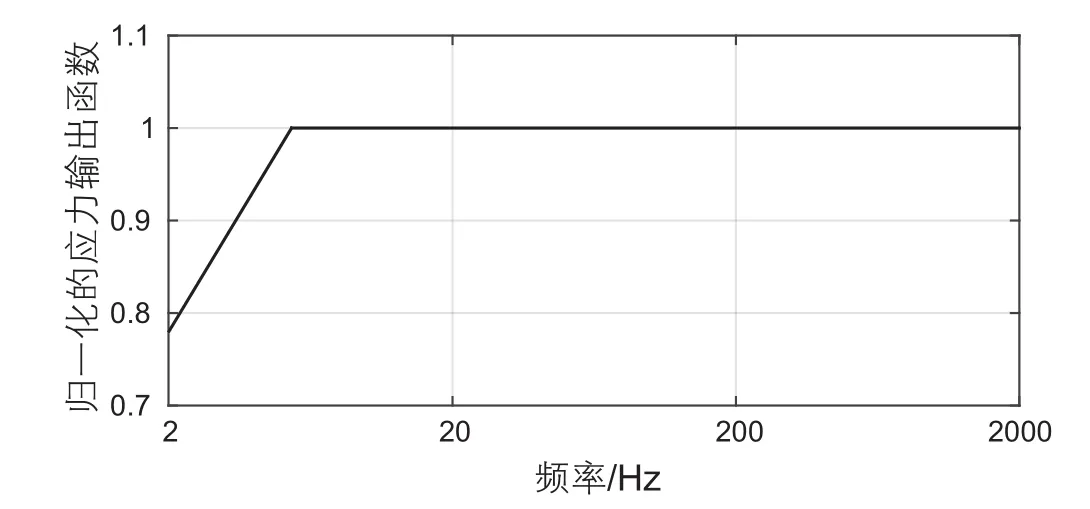
图2 归一化的应力输出函数Fig. 2 Normalized output-stress function for the shaker

图3 新旧增益函数(a)及对应的实测应力输出(b)Fig. 3 New and original gain functions (a)and corresponding real output stresses (b)

1.2.2 高效采集弱应变信号

系统测量的信号通常存在较大的随机噪音。为了更好的压制噪音和精确高效选取有效信号，对原有采集方法进行了分析改进。原有程序采用快速傅里叶算法(FFT)进行数据采集[22]，FFT算法是一种在频率域处理信号的常用方法，其根据激发信号的频率，通过简单的频率域滤波方法将有效信号提取出来。该算法计算稳定、简单，但需要足够的采样长度压制吉普斯现象，以达到高分辨率。然而，实验周期过长使得测量难以在同一状态下进行，实验结果的可靠性大大降低。因此，有必要寻找短周期、高信噪比的数据采集方法。

为了准确高效识别有效信号，采集方法采用了数值锁相环算法(Phase-Locked Loop, PLL)。PLL算法是基于物理锁相环算法开发，其具有对连续信号捕捉灵敏度高、时间短、精度高的特征。PLL算法具体实现流程如图4所示：(1)对于任意输入信号，系统给定参考信号(激发信号的频率)，让输入信号与参考信号相乘，通过三角函数变换，获得与输入信号、参考信号相位相减(加)相关的信号；(2)有效信号的频率与参考信号的频率相等，相减的相位变为恒定的相位差θ，部分信号变为直流分量；(3)通过低通滤波将直流分量滤出；(4)直流分量进一步运算可获得信号的振幅与相位，信号的频率为参考信号的频率，由此有效信号的信息全部获取。将PLL和FFT算法用于模拟实验(有效信号+白噪)进行有效信号拾取，固定采样频率fs=10 000 Hz，采样点数分别为N=2500及N=5000，结果如图5所示。从图5可以看出，当采样点数N=2500时，FFT算法受采样点数干扰，拾取有效信号的振幅极不稳定，当采样点数N=5000时，采样点数增加，分辨率提高，拾取有效信号的振幅变得稳定；PLL算法则不受采样点数的限制，在N=2500及5000时拾取有效信号的振幅都极为稳定。由此可知，PLL算法拾取有效信号不需要长时间对信号进行采样以达到足够高的分辨率，能够大大减少采样时间，因此系统选用了PLL算法高效采集弱应变信号。

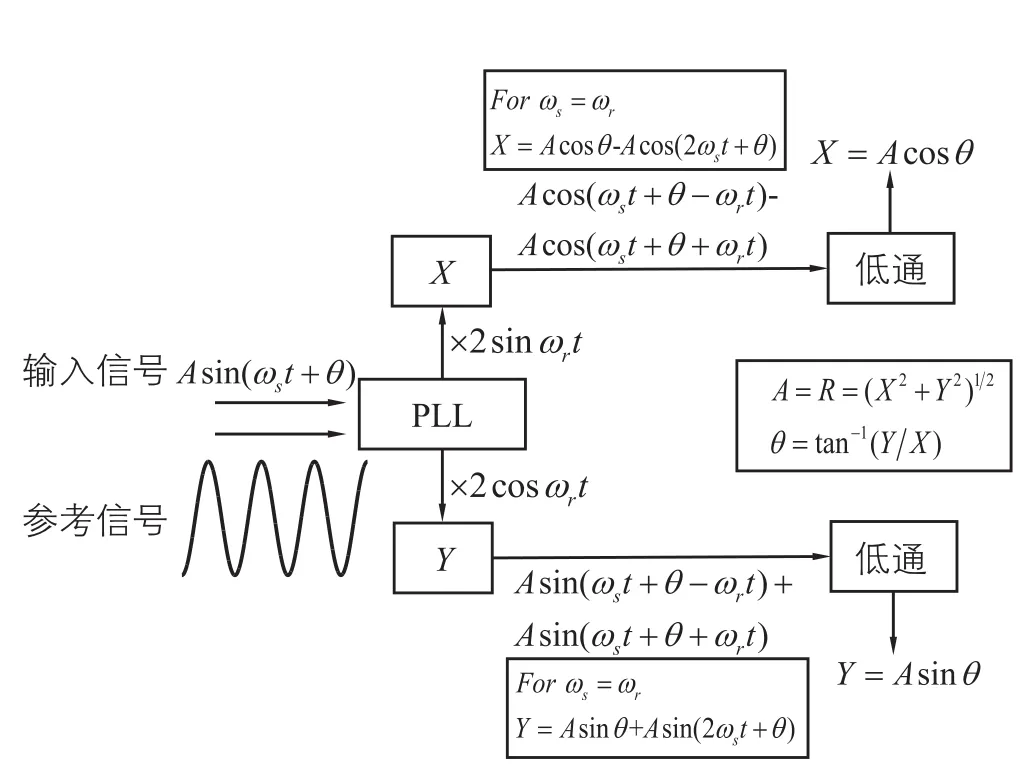
图4 锁相环算法流程图Fig. 4 Phase-Locked Loop (PLL)algorithm flow

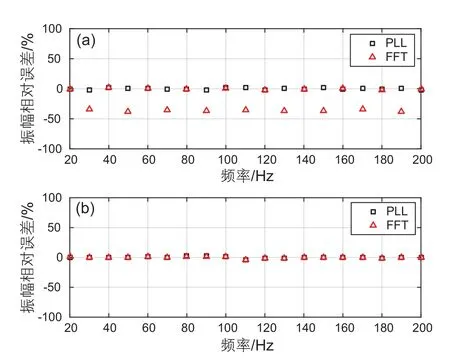
图5 利用PLL算法与FFT算法分析模拟结果误差对比(a)采样点数N=2500, (b)采样点数N=5000Fig. 5 Comparison of errors using PLL algorithm and FFT algorithm (a)N=2500, (b)N=5000

1.3 标定实验

为了检验改进后的低频地震岩石物理测量系统可靠性和准确性，利用标准样品(铝样和有机玻璃)在测量频段1～2000 Hz进行了标定实验。标准样品与Yin等的标准样品属于同一铸造批次，测量结果如图6所示。铝样为完全弹性体，它的弹性性质不随频率的变化而发生改变。在测量频段1～2000 Hz内，可以观察到铝样的杨氏模量和泊松比几乎不随频率发生变化，杨氏模量和泊松比的均值为71.1 GPa和0.334；由超声纵横波速度获得的杨氏模量和泊松比分别为71.8 GPa和0.332，对比可知，低频地震岩石物理系统测量铝的杨氏模量和泊松比都在合理误差范围(2%)内。此外，与Yin等测量的铝样数据相比，改进后系统测量获取的数据变得相对稳定。有机玻璃是典型的黏弹性体，弹性性质随着频率的变化而变化。在1～2000 Hz频段范围内，测量获取的有机玻璃杨氏模量随着频率的增加而增加，而泊松比随着频率的增加而缓慢降低，表现出与Yin等测量结果良好的一致性，说明改进后系统测量的有机玻璃数据同样是真实可靠的。标准样品的标定实验验证了改进后的低频地震岩石物理测量系统数据测量的可靠性和准确性，因而可有效开展低频岩石物理实验。

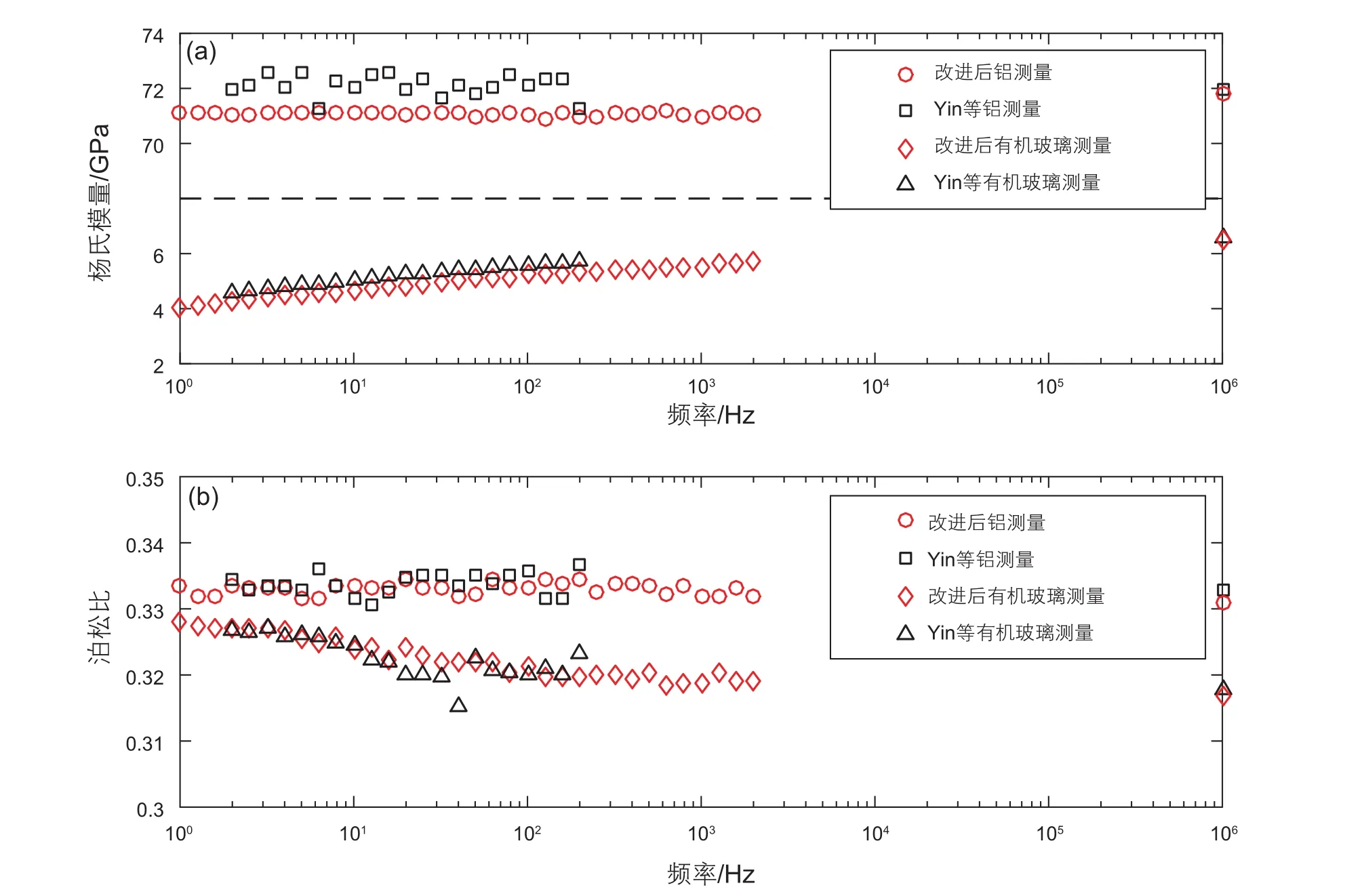
图6 标准样品(铝和有机玻璃)的标定实验(a)杨氏模量，(b)泊松比Fig. 6 Calibration experiments for the standard samples (aluminum and lucite) (a)Young’s modulus, (b)Poisson’s ratio

2 致密砂岩岩石物理实验

改进后的测量系统在标准样品标定后，为了进一步验证系统的可靠性和准确性，同时建立针对致密砂岩的低频岩石物理实验与分析流程，本文以一块中国东部某油田致密砂岩为例，在1～2000 Hz频段和1 MHz频率及不同压力下对干燥和饱和白油致密砂岩开展了岩石物理实验。这里仅研究了饱和单一流体、压力因素对致密砂岩弹性性质的影响，如果研究其它如饱和度、流体类型及黏度等因素对致密砂岩弹性参数的影响，可以仿照类似的实验和分析流程。

2.1 实验样品

致密砂岩岩样主要成分为石英及长石，泥质胶结，胶结较为致密(见图7)。岩样为圆柱状，主要物理性质如表1所示，颗粒的体积模量由Voigt-Reuss-Hill平均获得。

图7 致密砂岩岩样(制备岩样用于低频实验)Fig. 7 The tight sandstone sample (the present sample was used in low-frequency experiments)

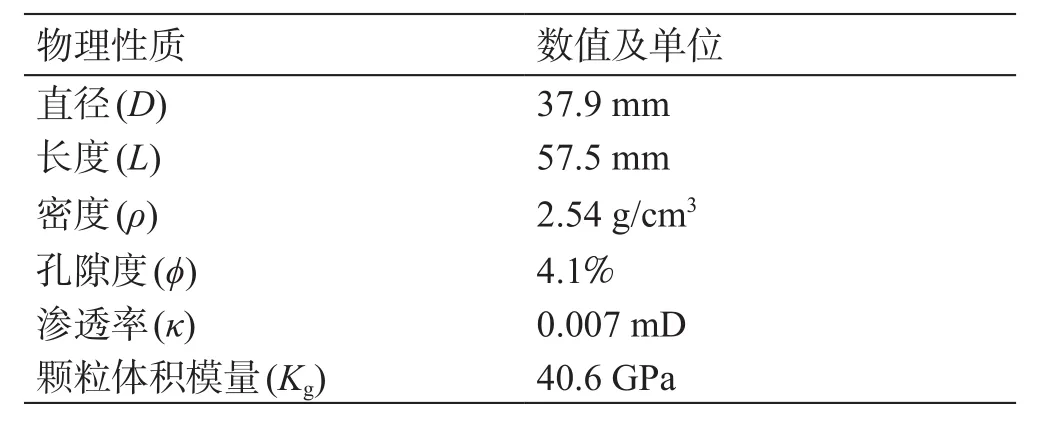
表1 致密砂岩岩样物理性质Table 1 The physical properties of tight sandstone sample

2.2 实验流程

实验前，岩样放在烘干箱中烘干3天，烘干温度为80 ℃，然后将岩样置于实验室中润湿2天。首先，在不同压力下(0.1～50 MPa)利用超声脉冲透射法测量了干岩样的超声纵横波速度，超声脉冲的频率为1 MHz。干岩样超声速度测量完成后，在岩样侧面涂一层均匀的薄胶封闭岩样侧边界，两端与标准铝样用胶固定(见图1)。在标准铝样和岩样贴完应变片及焊接相关导线后，利用环氧树脂将其包裹，阻隔围压气体渗入岩样及保护应变片。最后，将整个实验岩样固定在低频地震岩石物理测量系统中。在不同围压下(0.1 MPa, 5 MPa, 10 MPa)，获取岩样 1～2000 Hz频率范围内的弹性参数。测量完成后，将岩样从测量系统取下，与Yin等类似[22]，利用加压饱和方式对岩样进行白油饱和(白油黏度为65 cP)。饱和一定时间后，将岩样取出擦净称重，如果重量不再增加说明岩样已经完全饱和；否则，继续加压饱和。在饱和白油完成后再次将实验样品固定在测量系统中进行低频测量。低频测量完成后，将岩样从环氧树脂中取出，利用超声透射法获取饱和白油岩样超声纵横波速度。

2.3 实验结果

2.3.1 超声结果

不同压力下，岩样在干燥和饱和白油两种状态下的超声纵横波速度如图8所示。干岩样纵横波速度在低压时(0.1～20 MPa)随着压力增加而增加较快，呈非线性变化；在中间压力段(20～45 MPa)随着压力的增加而增加变缓，近似线性增加；45 MPa以后，纵横波的速度不再随着压力的增加而增加。相对于干岩样纵横波速度，饱和岩样的纵横波速度变化相对比较平缓。干燥与饱和岩样的纵波速度差异随着压力的增加而减小；饱和岩样的横波在压力较小时大于干燥岩样的速度，随着压力的增加，差异逐渐减小，在大约20 MPa后，饱和岩样的横波速度小于干燥岩样的横波速度，速度差异随压力继续增加略有增加。干岩样纵横波速度随着压力增加的变化趋势反映了岩样内微观孔隙结构对不同压力的响应[25]，利用这一压力变化趋势，可以估计岩样内软孔隙的纵横比及其分布，为后续的岩石物理模型模拟提供基础。

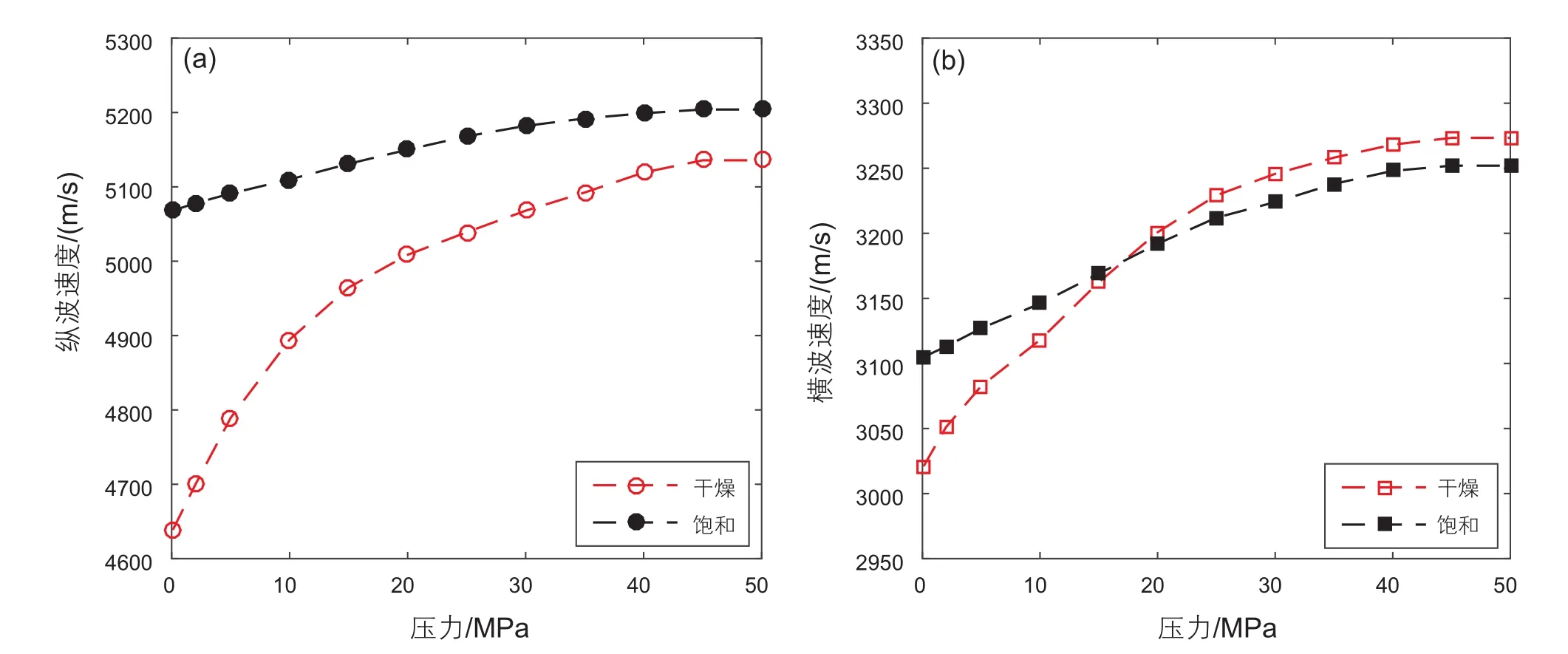
图8 不同压力下超声纵横波速度(a)纵波速度，(b)横波速度Fig. 8 Ultrasonic P-wave and S-wave velocities at different pressures(a)P-wave velocity, (b)S-wave velocity

2.3.2 低频结果

图9 不同压力下干岩样低频和超声测量结果(a)杨氏模量，(b)泊松比，(c)纵波速度和(d)横波速度Fig. 9 The measured low-frequency and ultrasonic results for the dry sample at different confining pressures (a)Young’s modulus, (b)Poisson’s ratio, (c)P-wave velocity and (d)S-wave velocity

图9展示了干岩样在不同压力下1～2000 Hz频段范围内低频地震岩石物理系统测量的杨氏模量、泊松比、纵波速度和横波速度，同时展示了相应的超声频率杨氏模量、泊松比及纵横波速度。从图9中可得：随着压力增加，各个弹性参数增加；各个弹性参数在1～2000 Hz频段内略有频散，可以忽略不计；低频系统测量的弹性参数略小于超声测量的弹性参数，误差在合理范围内(2%)，二者表现出良好的一致性。低频测量获取的干岩样弹性参数几乎无频散且低频测量数据与超声测量数据的一致性再次验证了低频测量系统的可靠性和准确性。

图10展示了饱和白油岩样低频系统测量的杨氏模量、泊松比、纵横波速度及相应的超声实验结果。从图10中可以看出：(1)各个弹性参数随着压力的增加而增加，有着相似的压力变化趋势；(2)各个弹性参数在测量频段范围内(含地震频段)都呈现出明显的频散特性；(3)各个弹性参数的频散量随着压力的增加而逐渐减小，纵波速度在不同压力(0.1 MPa、5 MPa、10 MPa)下 的 频 散 量 分 别 为 192.4 m/s、 166.0 m/s、117.4 m/s，横波速度的频散量分别为46.1 m/s、36.35 m/s、16.9 m/s；(4)随着压力的增加，各个弹性参数的频散频段向更低频率移动，这可能反映了压力的增加使岩样软孔隙闭合，岩样软孔隙纵横比移向更小值。

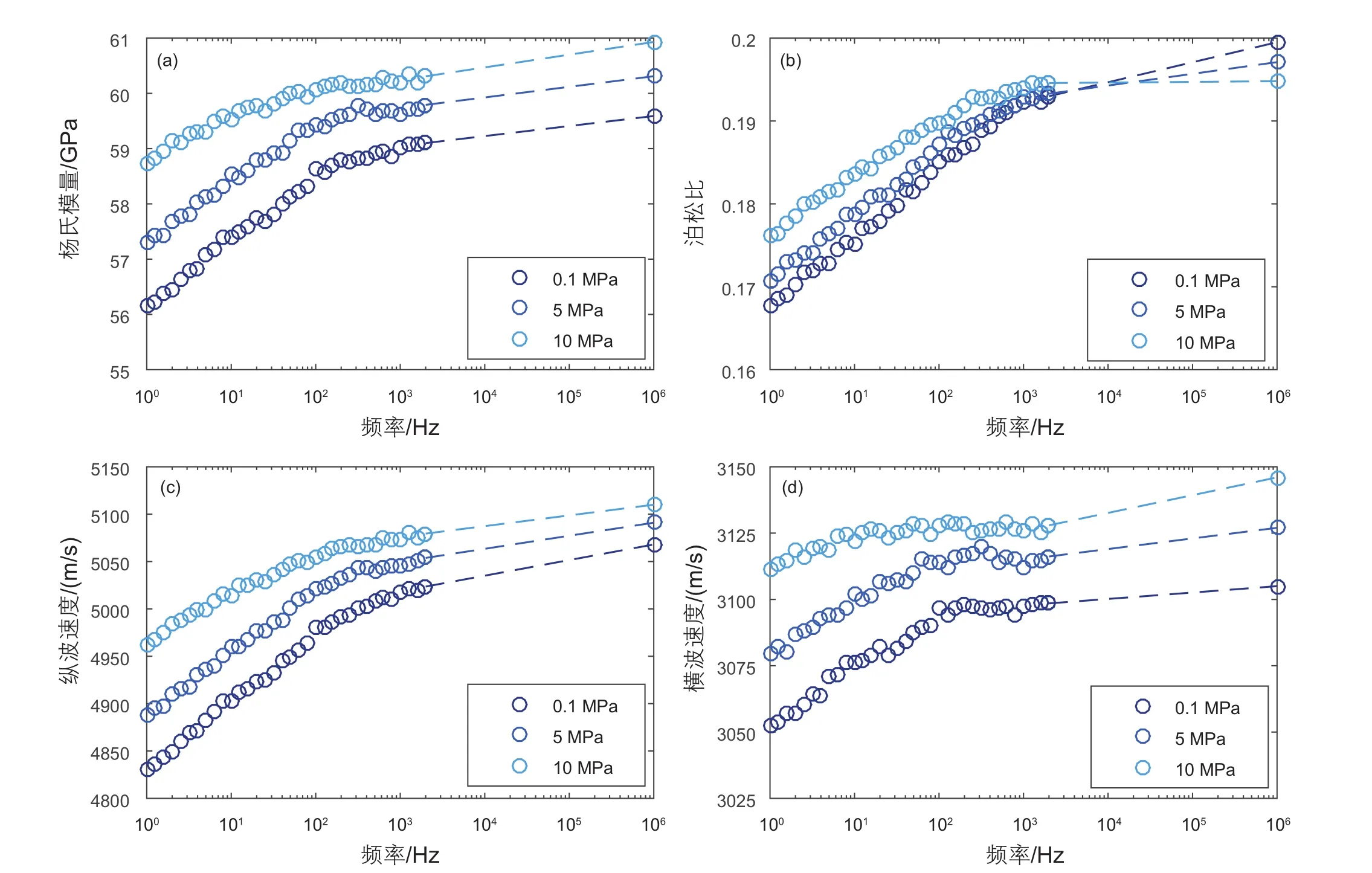
图10 不同压力下饱和岩样低频和超声测量结果(a)杨氏模量，(b)泊松比，(c)纵波速度和(d)横波速度Fig. 10 The measured low-frequency and ultrasonic results for the oil-saturated sample at different confining pressures (a)Young’s modulus, (b)Poisson’s ratio, (c)P-wave velocity and (d)S-wave velocity

3 岩石物理模型模拟对比分析

饱和白油致密砂岩的弹性参数频散频段随着压力的增加而向低频移动，与Yin等观测到饱和甘油致密砂岩的弹性参数频散随压力的变化特征一致，其通过将实测纵波速度与Gurevich等的喷射流模型对比，论证了喷射流是引起饱和流体致密砂岩频散衰减的主要原因。Gurevich等将岩石孔隙结构理想化为硬孔(纵横比α＞0.01)和软孔(纵横比α＜0.01)组成的双孔隙结构，构建了简单的喷射流模型用以解释饱和流体岩样由微观尺度上流体流动引起的频散衰减现象[12]，但模型计算采用单一的软孔隙纵横比和软孔隙含量脱离了实际情况。考虑到软孔隙不同的纵横比和含量，邓继新等提出基于微观孔隙结构特征的喷射流模型[26-27]，这一模型合理解释了不同压力下饱水致密砂岩的超声纵横波速度。基于微观孔隙结构特征的喷射流模型预测速度频散不存在明显的低频段与中间频段，速度随着频率的增加而递增，即使在地震频段，也会出现速度频散现象，这一预测与我们低频测量结果相一致，为了进一步理解饱和白油致密砂岩的频散特征及机制，本文由此选用基于微观孔隙结构特征的喷射流模型进行模拟，并将模拟结果与实测纵横波数据对比分析。

3.1 基于微观孔隙结构特征的喷射流模型

邓继新等依据孔弹性理论计算了不同压力下不同软孔隙的纵横比及其含量[26-27]：

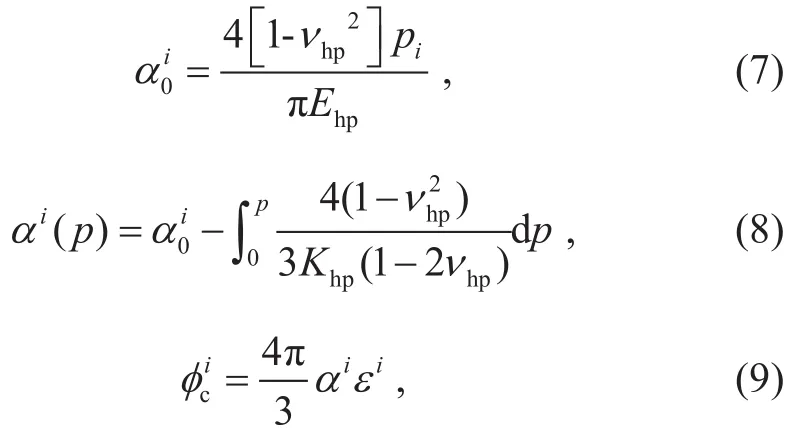
其中，表示初始压力(0.1 MPa)下的软孔隙纵横比分布，νhp表示高压下的干岩样泊松比(此处选择50 MPa压力下的超声纵横波速度获得，下同)，Ehp表示高压下的干岩样杨氏模量，pi表示不同的压力，αi(p)表示压力p下的软孔隙纵横比分布(p＞初始压力)，Khp表示高压下的干岩样体积模量，αi表示某一软孔隙纵横比，εi表示αi对应的裂隙密度，表示纵横比为αi软孔隙的孔隙度。

在获得软孔隙纵横比分布及含量后，利用迭代的方式将分布的软孔隙带入到Gurevich等(2010)提出的改进“干骨架”中[12,27]：

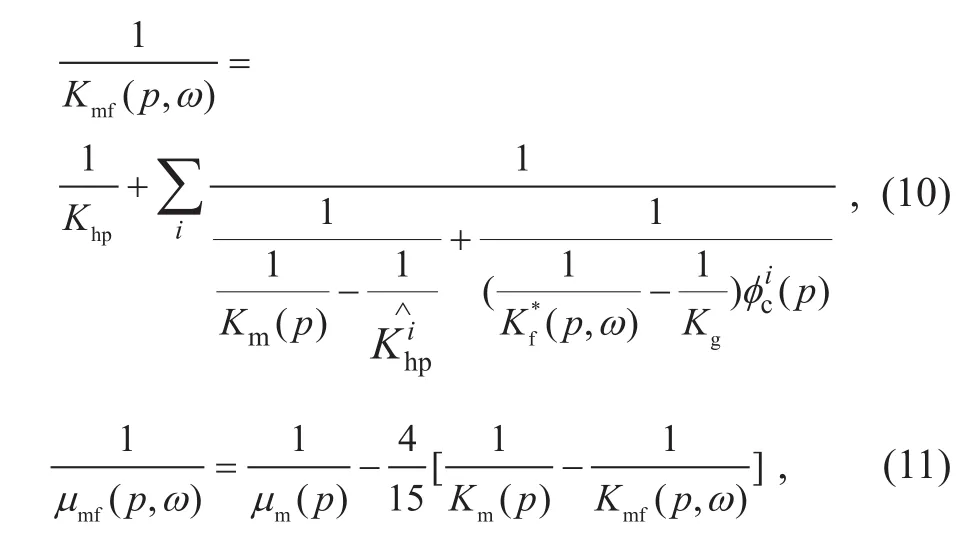
其中，Kmf(p,ω)表示压力p下改进“干骨架”体积模量，Km(p)表示压力p下干岩样体积模量，表示不含第i项软孔隙的高压下体积模量，Kg表示颗粒体积模量(40.6 GPa)，(p)表示压力p下第i项软孔隙的孔隙度，(p,ω)表示压力p下有效流体模量(具体求解参见Gurevich等[12])，µmf(p,ω)表示压力p下改进“干骨架”剪切模量，µm(p)表示压力p下干岩样剪切模量。

获得改进“干骨架”模量后，将其带入Gassmann方程(12)、(13)中可以获得饱和流体岩样的体积模量和剪切模量[12]，进一步由公式(5)和(6)获得饱和流体岩样频变的纵横波速度。

其中，Ksat(p,ω)表示压力p下饱和岩样体积模量，φs表示岩样的硬孔隙度，Kfl表示孔隙流体(白油)的体积模量(1.9 GPa)，µsat(P,ω)表示压力p下饱和岩样剪切模量。

3.2 模型模拟与实测结果对比

依据公式(7)-(9)，首先利用干岩样超声纵横波数据获得了不同压力下(0.1 MPa、5 MPa、10 MPa)的软孔隙纵横比分布及其孔隙度。图11展示了致密砂岩岩样的软孔隙纵横比分布及其孔隙度。对喷射流起主要作用的纵横比一般在10-5～10-3之间[28]，实验获得的软孔隙纵横比在合理的区间范围内。随着压力的增加，软孔隙的含量整体降低，降低趋势与低频实验中弹性参数频散量降低趋势相一致。此外，纵横比大小随着压力的增加整体向更低值移动，与低频实验中弹性参数频散频段向更低频率移动相一致。

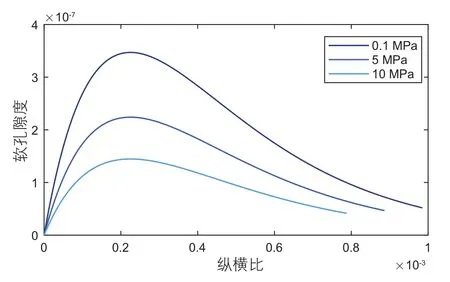
图11 软孔隙纵横比分布及其孔隙度Fig. 11 The aspect ratio distribution and porosity of soft pores

获得岩样的软孔隙纵横比分布及其含量(孔隙度)后，将其带入到基于微观孔隙结构特征的喷射流模型，计算获得了模拟纵横波速度，并将其与实测纵横波速度进行了对比，如图12所示。从图12中可以看出，模型能够大致模拟致密砂岩实测纵横波速度，模拟结果与实测纵横波速度表现出相似的频散特性，二者皆表现出随着压力增加频散频段向低频移动的趋势，表明喷射流是造成饱和白油致密砂岩频散的主要原因。

具体来讲，实测横波速度与模拟结果吻合较好，不同压力下的横波速度与模拟的结果都在合理的误差范围内，二者都表现出较小的频散；实测纵波速度与模拟结果有着一定的偏差，实测纵波速度的频散特征比模型模拟更加明显且频散频段更为宽广，造成这一现象的原因可能是实际岩石的孔隙结构比理论模型更加复杂，还需进一步深入研究。

图12 实测纵横波速度与模拟结果对比(a)纵波速度，(b)横波速度Fig. 12 Contrast of the measured P- and S-wave velocities and the modelling results (a)P-wave velocity, (b)S-wave velocity

4 结论

通过优化激振器增益函数和选取高效的锁相环算法改进了低频地震岩石物理测量系统，使系统测量频段拓展到1～2000 Hz并减少了采集时间。标准样品(铝和有机玻璃)的标定实验验证了改进后系统的可靠性和准确性。基于改进后系统对致密砂岩在干燥和完全饱和白油状态下开展了低频岩石物理实验，获取了1～2000 Hz频段范围内的杨氏模量、泊松比及纵横波速度。干燥致密砂岩的弹性参数与超声测量结果表现出良好的一致性，而饱和白油致密砂岩不同弹性参数皆表现出明显的频散性质。利用微观孔隙结构特征的喷射流模型模拟饱和白油岩样纵横波频散特征，并与实测的纵横波速度进行了对比分析。分析表明：喷射流主导了饱油致密砂岩的速度频散；横波模拟结果与实测横波速度相对吻合，纵波模拟结果与实测纵波速度存在一定偏差，实测纵波速度的频散特征更加明显及频散频段更为宽广，可能是实际岩石的孔隙结构比理论模型更加复杂造成的。改进后的低频地震岩石物理测量系统能够在宽频带范围内定量研究含流体岩石的弹性参数频散特征，为建立储层弹性参数与地震响应之间定量关系及发展储层预测和流体识别新技术奠定了重要的基础。