农村小学生几何直观能力的培养策略研究

许缤红

摘要：近年来，核心素养已成为教育界关注的重要话题，而直观想象就是数学核心素养之一。一直以来，我国农村小学生的几何直观比较薄弱，提高农村小学生的几何直观是一项刻不容缓的任务，而农村小学生有自己的特点，我们更应着重根据农村小学生的特点进行有针对性的培养。

关键词：农村;小学生;几何直观;策略

中图分类号：G623.5文献标识码：A     文章编号：1992-7711（2019）09-075-2

几何直观是一种特殊的的直观，是借助于见到的或想到的几何图形的形象关系而产生的对数学研究对象的感性认识。我发现教学中存在农村小学生在遇到稍显复杂抽象的数学问题时，难以将它与直观形象的图形语言结合起来。农村小学生缺乏用图形语言表达的能力，在用图形语言来描述抽象的数学问题时，往往表达不清楚等问题。通过课题研究，我认为，可采取下列解决策略。

一、注重几何直观与数学本质的沟通

1.在图形教学中发展几何直观

在教学中，我们发现质数和合数的概念比较抽象，很难结合具体的生活情境展开，对学生来说有一定难度。因此，这节课通过直观形象的图形引入新课，在观察操作中明确了能否拼成两个以上的图形与因数有关，使学生初步感受质数合数的本质。例如，笔者在教学《质数和合数》一课中，创设了这样的教学情境：用几个边长1厘米的小正方形拼成一个长方形或正方形。学生先动手操作，再组织交流，让学生说说自己的想法：每排摆了几个，共摆了几排。根据学生的回答，课件出示相对应的图形。（1）面积是2平方厘米时，拼成的是长2厘米、宽1厘米的长方形。（2）面积是3平方厘米时，拼成的是长3厘米、宽1厘米的长方形。（3）面积是4平方厘米时，拼成的有两种，一种是长4厘米、宽1厘米的长方形，另一种是边长2厘米的正方形。……引导学生观察图形，思考：能否拼成两个以上图形与什么有关？学生通过观察发现，只能拼成一种图形（长方形）的面积分别是2、3、5、7平方厘米，能拼成两个以上图形的面积分别是4、6、8、9平方厘米。由此看来，可以把这些数分成两类。根据已有的知识经验，学生不难发现，2、3、5、7這些数只有1和它本身两个因数，而4、6、8、9这些数的因数超过了两个，进而初步感知质数与合数的本质。

2.在数学运算中发展几何直观

例如，在教学《分数乘分数》时，笔者创设了这样的情境：我们教室的后面有一块什么地呢？（菜地）现在老师准备分一小块一小块来种各种各样的菜，你们想知道老师是怎么分的吗？（课件出示例4图）

提问：请同学们观察，涂色部分占这个长方形的几分之几？

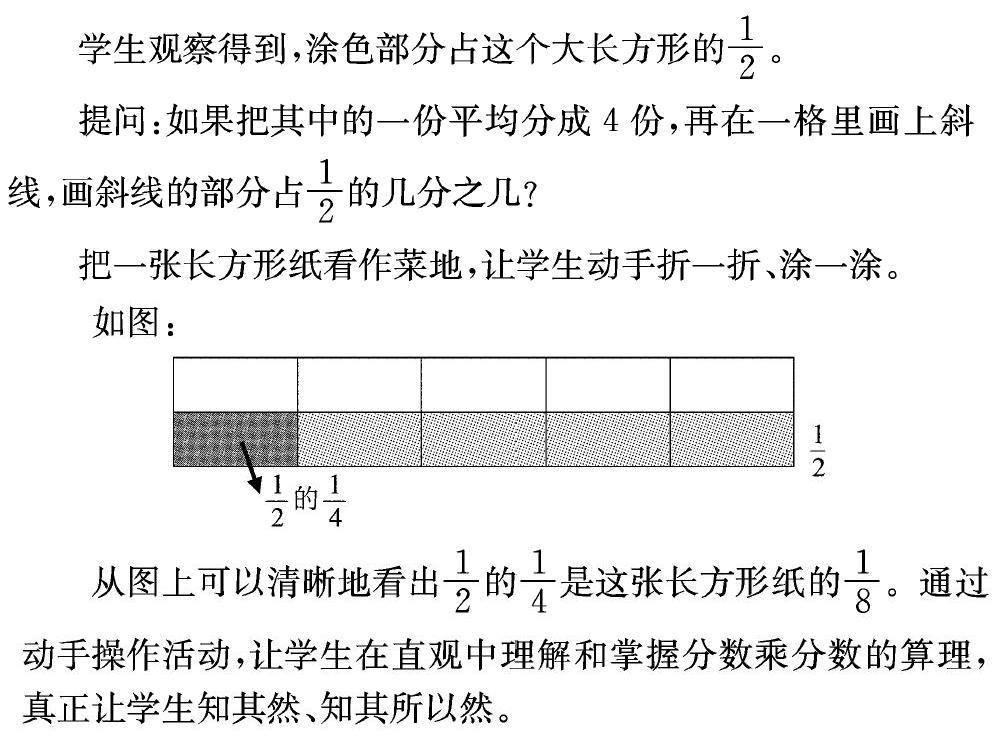
学生观察得到，涂色部分占这个大长方形的12。

提问：如果把其中的一份平均分成4份，再在一格里画上斜线，画斜线的部分占12的几分之几？

把一张长方形纸看作菜地，让学生动手折一折、涂一涂。

如图：

从图上可以清晰地看出12的14是这张长方形纸的18。通过动手操作活动，让学生在直观中理解和掌握分数乘分数的算理，真正让学生知其然、知其所以然。

对于学生来说，记住计算法则并不困难，但要理解算理有一定的难度。除了分数乘分数，乘法交换律，乘法分配律等运算教学中，我们都可以借助直观图形，让学生充分体验从直观图形到抽象的算理的演变过程，不断提高学生的几何直观能力。

二、注重几何直观在数学学习中的运用

1.加强学生的观察与操作

几何直观的形成和发展依赖于学生的观察、分析、操作，并结合自身经验形成的对问题的感性认识。例如，在教学《认识线段》时，笔者设计了这样的教学环节：

师：看，老师给大家带来了什么？（一根毛线）把这根毛线轻轻地放在桌子上，它的形状是怎样的？（弯的）。那你有办法把它变成直的吗？请拿出准备好的毛线试一试。

学生摆弄，尝试把毛线变直。

师：变直了吗？谁上来演示给大家看看。

学生用手捏住线的两头，向两边拉紧。

师：如果我们把一只手松开，毛线还直吗？如果改变毛线的方向（横、竖、斜不同方向），毛线还直吗？

比较：这样拉出来的线与原来那跟线有什么不同？

这样层层递进，使学生在观察、操作、分析和想象活动中进一步认识了线段的基本特征，让学生对线段有了从形象到抽象的理性认识，培养了学生的几何直观。

2.紧密联系生活实际

数学来源于生活，学生在实际生活中积累了一定的几何知识经验，这就构成了他们发展几何直观的重要依据。因此，在教学中，教师应充分研读教材，将教学内容与学生的生活实际紧密联系起来。

例如在教学《角的认识》一课中，一位老师设计了这样的教学环节：

找一找生活中的角

师：你身边的哪些物体上有角呢？谁愿意来说一说。

学生自由发表意见说说自己见过的生活中的角（也可以找找教室里的角）。

生：数学书上有角，三角尺上有角、钟面上有角等。

师：请你用手指一指。（教师注意动作的引导和示范。）

师：老师这也有几个物体，请你仔细观察一下，它们上面有角吗？

师：你在剪刀的什么地方找到了角？给老师指一指。我们把它请出来。（课件出示）

师：钟面上的角藏在哪儿？（让学生找出两根针组成的角）

生：时针和分针组成了一个角。

师：我们把它请出来（课件出示）。

以学生的生活实际为背景，找一找生活中的角，逐步抽象成几何图形，符合学生的认知发展规律，让学生对角的认识也更加深刻。

3.有效运用现代信息技术

数学教材中有些内容是抽象难懂的，而信息技术恰恰能解释那些教师难以讲清，学生难以理解的知识，它能将抽象的知识通过形、声、情、意形象化，让学生直观感知数学问题，有利于优化学生的认知过程，培养学生的几何直观能力。

例如，在教学《直线、射线、线段》时，一位老师在课的开始，拿出了生活中常见的电筒，让学生观察电筒射出的光线，从一点出发，射向教室的墙上，再射向天空，学生说说这条光线是怎样的？根据已有的生活经验，学生能直观的感知这条光线是从一点出发到另一点，但很难感受它是无限延伸的。而另一位老师则创设了这样的情境，利用多媒体课件出示浩瀚的宇宙中，一束激光从地球射向月亮，能测量出地球到月亮的距离。假如月亮不见了，这束光会如何？学生感受到它会一直延伸。两节课都用到了光线，然而起到了不同的效果。通过多媒体课件演示，有利于帮助学生理解射线是将一条线段的一端无线延长所形成的图形。这样利用信息技术化虚为实、化抽象为具体的特点能为学生的学习提供了直观例证，不仅给学生渗透了极限思想，而且丰富了学生的几何直观。

几何直观是小学生必备的一种数学素养。提高农村小学生的几何直观是一个长期的过程，我将坚持把几何直观的培养贯穿于自己的数学教学过程中，落实到课堂教学的细节之处，以促进学生几何直观的提升和素养的形成。

[参考文献]

[1]徐利治.谈谈我的一些数学治学经验[J].数学通报，2000（05）.