浅圆仓横向和垂直通风数值模拟对比研究

戚禹康，王远成，俞晓静

(山东建筑大学热能工程学院，山东济南250101)

0 引言

1994年在辽宁试建了第一座浅圆仓，并从1998年起国家开始大规模地建设储备粮库。目前，已有90个粮库新建或续建约720个浅圆仓，其仓容达5.69×109kg[1]。浅圆仓仓内直径一般≥20 m，仓壁高度与仓内直径之比≤1.5[2]。我国传统仓型多为平房仓，具有隔热、保温性能好和储粮稳定的特点。浅圆仓作为新引进的仓型，与平房仓相比，多采用钢筋混凝土条形基础，仓顶为聚乙烯夹心预制装配整体式钢筋锥面薄壳，能将粮食对壁面推力转换成对环钢筋的拉力，充分发挥钢材抗拉强度大的特点[3]。浅圆仓可以采用较少的常规输送机械组合，以较低的运行成本完成粮食的入仓和出仓作业，在配备了机械通风、环流熏蒸等新技术装备后，比较容易实现现代化仓储管理。浅圆仓占地面积较小、堆粮高度高、仓间不需再留道路，因此吨粮土建投资与平房仓相近[4]。所以，浅圆仓已成为我国近年来大力发展的一种新仓型。然而，由于浅圆仓粮层高、单仓储量大，给冬季通风降温带来了许多新问题。目前，国内常用的浅圆仓通风方式为在仓底设置地槽风道的垂直通风，但由于仓壁高度与仓内直径之比约为1.5，所以垂直通风的空气流动距离较长，通风过程中温度、水分分层现象较为明显，可能会出现顶部的粮食温度还未达到标准，但底部粮食已经过度干燥的现象[5-6]。为此，文章基于多孔介质流动理论，提出了横向通风的解决方案。通过在壁面安装垂直支风道使空气沿半径方向移动至粮仓中心的集风管内，再排到粮仓上部的空气区域。

目前，对通风时粮堆内部温度变化的模拟计算主要使用Thorpe建立的数学模型[7]，该模型可以较好地反映粮堆内部温度分布，文章也是在此模型的基础上构建数学模型。Gadton等[8]通过建立粮堆热湿耦合模型研究粮食内部温度变化。Jian等[9]研究了实验圆仓的温度、湿度和储藏周期等主要因素对油菜籽储藏状态的影响并建立了相关模型。Xu等[10]建立了筒仓内粮堆孔隙率对储粮通风系统均匀性影响的相关数学模型。Khankari等[11]研究了粮食水分和空气水分之间的传输关系，构建了与试验数据相符的水分传输模型。Jia等[12]在笛卡尔坐标系下建立了二维圆筒仓粮堆温度场模型。其研究结果对浅圆仓通风数学模型的建立有一定的参考作用。张燕君等[13]采用有限元数值模拟方法深入分析了在冬、夏不同季节平房仓的粮堆温度分布。李祥利等[14]模拟研究了“圭”字形风道垂直通风状态下粮堆温度和水分变化规律。王雪等[15]模拟了在内热源干扰下粮堆温度场分布及变化情况。白忠权[16]基于多孔介质局部热质平衡原理研究了浅圆仓中小麦粮堆在非人工干扰状态下温度、湿度分布及迁移变化规律。尹君等[17]利用实测粮温数据，通过Matlab模拟软件和粮温拟合算法，重现了浅圆仓粮堆场分布并根据温湿度场耦合理论分析预测储粮状态的短期变化，并基于温水分场耦合原理进行了分析。王远成等[18]和高帅等[19]建立了储粮通风模型，对粮堆内部空气流动及热湿耦合规律进行模拟研究，重点研究了房式仓垂直和横向通风过程中温度前沿的变化。陈桂香等[20]、王远成等[21]和任广跃等[22]运用CFD模拟技术，模拟分析平房仓的准静态储藏和浅圆仓机械通风2种状态下粮堆温度场、介质流场的分布及变化趋势。吴子丹等[23]提出采用粮堆多场耦合理论结合模型，可应用于各种仓型结构、结合粮堆实测温度值对粮堆状态进行短期预测，其研究结果对浅圆仓通风物理模型的建立以及模拟软件的选择和参数设置有一定的指导意义。尽管国内外对浅圆仓垂直通风时温度变化的模拟计算和实仓测试研究已经取得了一定进展，但缺乏对横向通风方式效果的模拟对比。

1 浅圆仓模型建立、条件设置与实际测点分布

以日照库浅圆仓为研究对象建立物理模型，其直径为30 m、檐高为30 m、装粮高度为20 m、仓顶倾斜角度为19°，仓顶有4个直径各为1 m的轴流风机出口。

1.1 浅圆仓垂直通风物理模型

底部风道为梳状铺设，分为2部分，每部分各设置1个进口，风道宽度为600 mm、高度为500 mm，出风面与粮仓地面平齐。浅圆仓垂直通风梳状风道平面布置如图1所示，浅圆仓垂直通风的物理模型如图2所示。

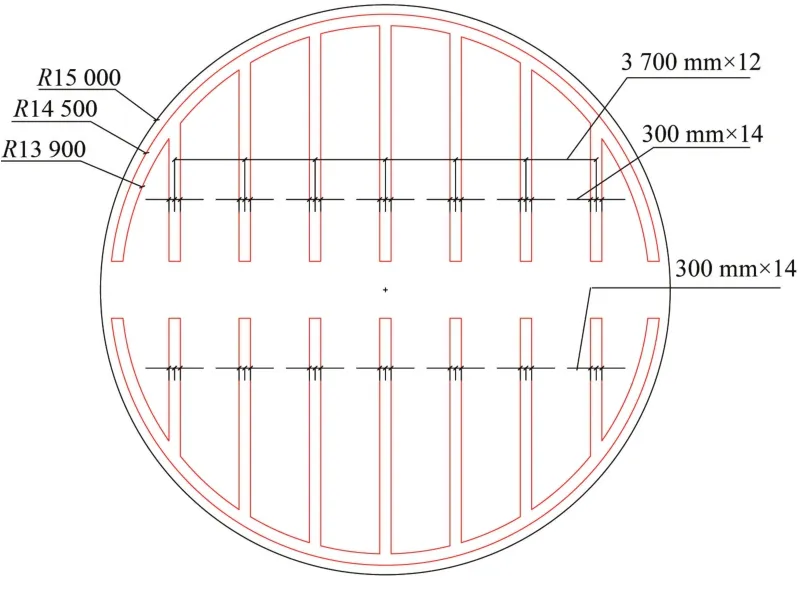
图1 浅圆仓底部梳状风道平面布置图

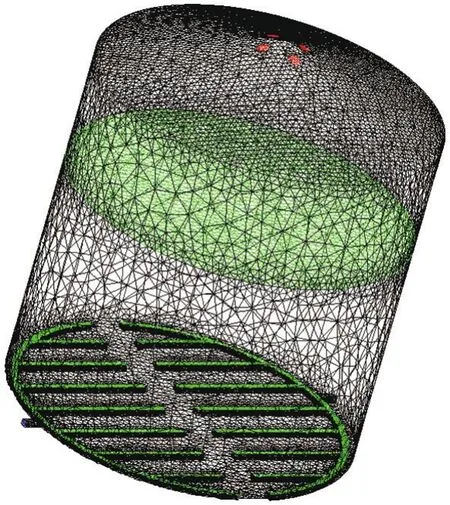
图2 浅圆仓垂直通风网格图

粮面及底部风道上侧面边界条件为可通过面，轴流风机出口为压力出口。由于使用ICEM软件可以比较简便地画出三维非结构网格，文章使用ICEM进行网格划分。采用四面体和六面体相结合的方式划分网格，在通风口和通风笼处加密，生成的网格数约为30万。

1.2 浅圆仓横向通风物理模型

浅圆仓横向通风时通过沿壁面垂直安装安装的8根支风道使空气沿半径方向移动至粮仓中心的集风管，共设2台风机，通过底层2个环形主风道将空气分别均匀地分配至4个支风道。集风管直径为2 m，考虑到底部需装设出粮机，集风管底部距粮仓底部距离为1 m。浅圆仓横向通风的物理模型如图3所示。

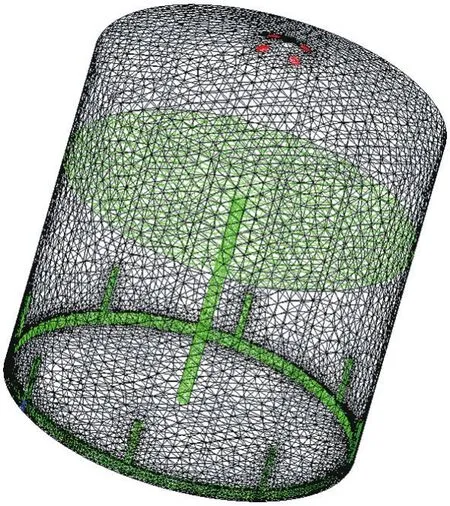
图3 浅圆仓横向通风网格图

粮面、通风笼、主风道内侧面及集风管边界条件为面，支风道顶面及主风道上侧面边界条件为壁面，轴流风机出口边界条件为压力出口。

使用ICEM进行网格划分，生成的网格数约为30万。

1.3 通风过程数学模型

1.3.1 连续性方程

小麦是一种典型的多孔介质，根据质量守恒理论，建立粮堆内的连续性方程，由式(1)表示为

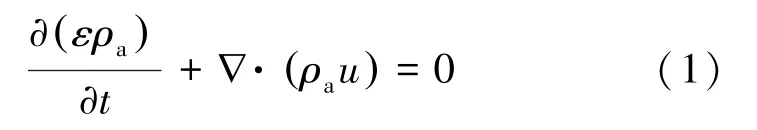
式中：ε为孔隙率，%；ρa为空气密度，kg/m3；t为时间，s；u为粮堆内部空气的表观速度或达西速度，m/s；∇为哈密顿算子。

1.3.2 动量方程

通风时粮堆内部强迫对流流动及其阻力的动量方程由式(2)表示为

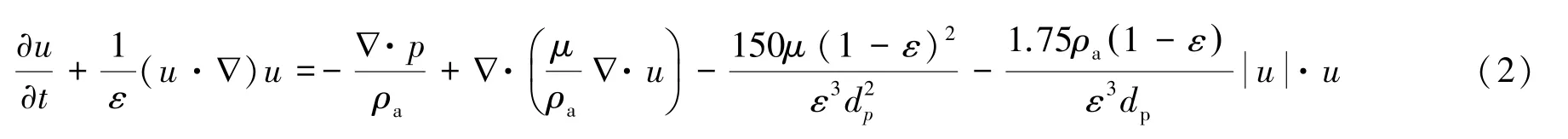
式中：p为压力，Pa；μ为空气的动力黏度，Pa·s；dp为谷物颗粒的等效直径，mm。

式(2)中，方程右边第3项为黏性阻力，第4项为惯性阻力，都是基于Ergun方程得到。当ε＝1时为空气区域流动方程，即N-S方程；当ε≠1时为粮堆区域流动方程，即达西-布林克曼方程。

1.3.3 对流传热方程

粮堆内的热量传递过程满足热力学第一定律，根据能量守恒方程可建立通风时粮堆内部热量传递的对流传热方程，由式(3)表示为

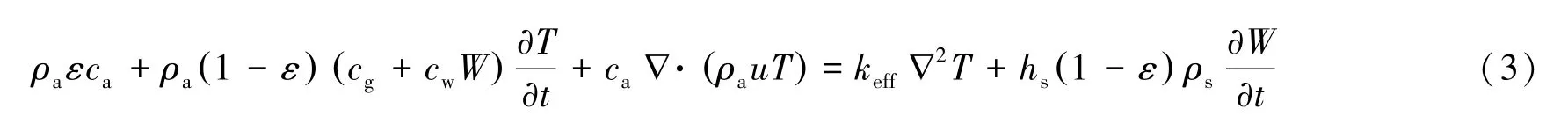
式中：ca、cg、cw分别为空气、粮食和水的比热，J/(kg·℃)；W为粮食的含水量；keff为粮堆的有效导热系数，W/(m·℃)；T为温度，℃；hs为粮食中每千克水的吸附热。式(3)中为热源项，即粮食吸湿和解吸湿时产生的热量。

1.4 数值模拟方法及初始、边界条件

采用非稳态计算法，共计算14 d，时间步长为10 s。为了防止迭代过程不收敛或数值不稳定，采用欠松弛技术。研究吨粮通风量选用5.2 m3/(t·h)。经计算，每个进口的风量为9.104 kg/s。进口温度为17℃，粮堆及空气区域初始温度为25℃，温差为8℃。

1.5 实际测点分布

将粮堆按半径1.5、5.5、9.5、13.5 m 分成4个环，由内到外分别设置3、6、12、18根，共计39根电缆，每根电缆均匀分布11个测点，共计429个测点，截面如图4所示。装粮9 000 t，吨粮通风量为5.2 m3/(t·h)。

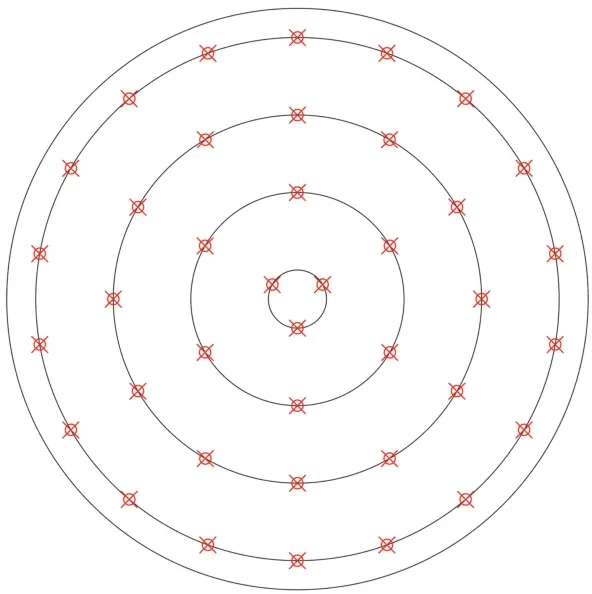
图4 浅圆仓测点分布截面图

2 结果与分析

文章主要对比垂直与横向通风7 d后的结果。底部梳状风道的速度分布图如图5所示。通风入口处风速较大，到环形风道末端风速逐渐降低。各支风道风速基本一致，通风均匀性较好。

图5 垂直通风底部梳状风道速度分布图

垂直通风第7天的速度和温度分布图如图6所示。由图6(a)中可以看出空气均垂直向上通过粮面，因为粮堆表观风速较为均匀，所以在粮堆的空气区域并没有产生涡流。由图6(a)～(d)中可以看出，由于仓底风道位置分布的关系，粮堆中部的区域温度降低的速率明显慢于两侧区域温度降低的速率。相比于横向通风，因为粮仓空气区域没有涡流，所以空气区域存在较大的温度梯度，且空气区域温度大于粮堆温度，中下部接近粮面处温度最高。垂直通风通风阻力计算方法为进口平均压力减去出口平均压力，为1 643.7124 Pa。

横向通风的底部环形主风道与支风道的速度变化图如图7所示。通风入口处风速较大，到主风道末端时，风速已逐渐降低。各支风道风速基本一致，通风均匀性较好。而且，相对于垂直地槽通风来说，横向通风不会出现通风死角，通风降温的均匀性大大提高。

横向通风第7天的速度、温度分布图如图8所示。从图8(a)中可以看出，在粮堆底部，空气沿水平方向进入集风管，但随着高度上升，空气无法水平进入集风管，更倾向于斜向直接通过粮面，支风管顶部的空气直接垂直上升通过粮面。由于集风管内流量升高，空气进入集风管的阻力逐渐提高，但集风管仍是十分必要的，如果没有集风管，空气短路的现象会更加明显。由于大部分空气从集风管排至粮仓空气区域，仓顶风口无法直接将空气排出，故会在仓顶空气区域产生在壁面向下的涡流。由图8(b)～(d)可以看出，粮堆中上部会形成一小块高温区域，这是由于空气都是斜向通过该区域，是空气在粮仓中的最长流动路线，阻力最大，所以通过该位置的风量较小。同时，该位置位于空气流动的末端，温度的降低会有延迟。比较图6和8可以发现，横向通风14 d后，粮堆上部的高温区明显小于垂直地槽通风，所以，横向通风的降温效果优于垂直通风。而且由于粮堆空气区域存在涡流的缘故，空气区域的温度也能较为均匀地降低。横向通风通风阻力计算方法同垂直通风通风阻力计算方法，为1 689.6016 Pa，与垂直通风阻力相近。这是由于文章模拟的装粮线高度较低，与半径长度接近，故与垂直通风相比没有明显优势。后续又针对半径为25 m、檐高为32 m、装粮高度为30 m的仓型进行了模拟，发现其横向通风阻力为1 614.96 Pa，垂直通风阻力为3 409.74 Pa。可以看出，当装粮高度较高时，横向通风通风阻力就会有明显优势。

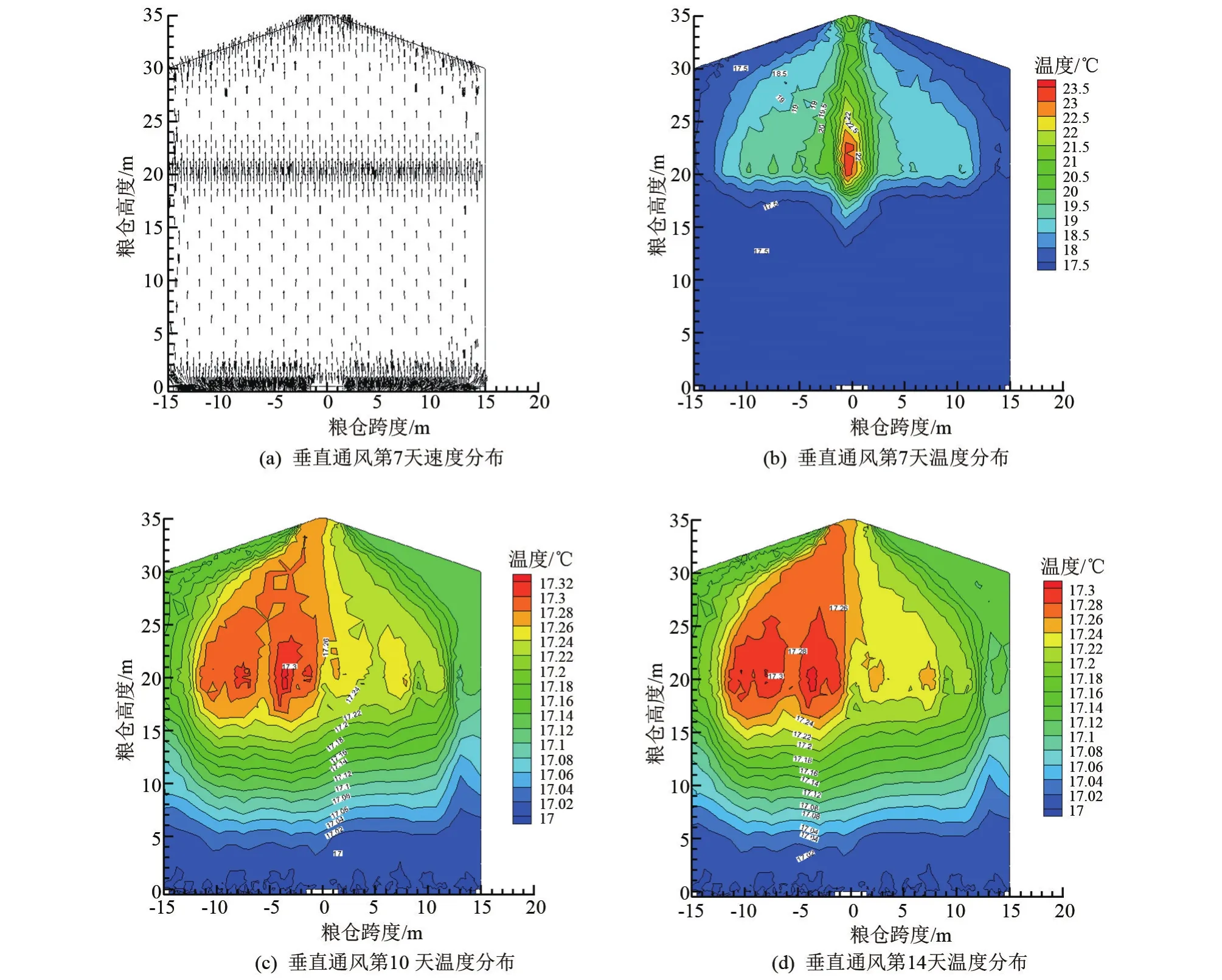
图6 垂直通风速度、温度分布图

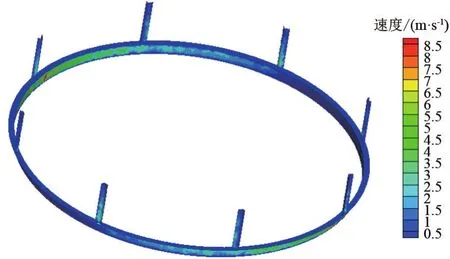
图7 横向通风环形主风道与支风道速度分布图

2种不同通风方式通风1～14 d的最高温度和平均温度模拟值以及通风实验实测温度对比如图9所示。可以看出，2种通风方式的粮堆平均温度变化基本一致，均在通风第7天时降低到15℃，并保持稳定。最高温度在第8天之前维持初始温度基本不变，这主要是由于通风前8天时，粮堆内部的温度无法均匀降低，所以部分区域仍保持初始温度。在第8天之后垂直通风平均温度的降低快于横向通风，垂直通风第10天时，粮堆最高温度就已经接近粮堆平均温度，而横向通风第14天时粮堆最高温度才接近粮堆平均温度。这主要是由于横向通风时，粮堆中上部的一小块区域温度无法快速降低，但由于此区域体积很小，对整体的平均温度没有显著影响，且在第10天时最高温度已降低至19℃，与平均温度的温差仅为2℃，在可接受范围内。通过模拟值与实测值的对比可以看出，模拟值与实测值较为接近，模拟结果是可靠的。

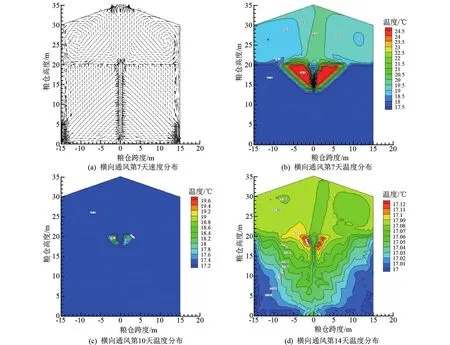
图8 横向通风速度、温度分布图

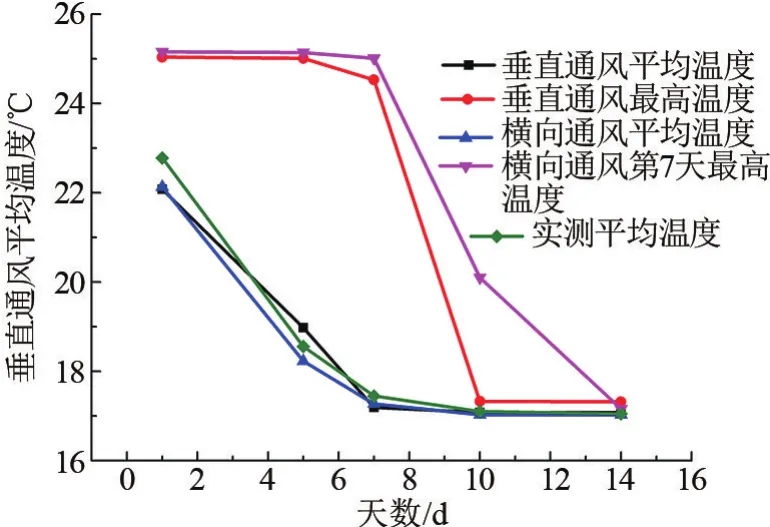
图9 垂直、横向通风1～14 d最高、平均温度模拟值及通风实验实测温度对比图

3 结论

通过上述研究得出以下结论：

(1)垂直与横向通风的平均温度变化趋势基本一致，且均在第7天时降低到15℃。受空气流动影响，横向通风时粮堆中上部存在一小块高温区域，但由于其体积很小，对平均温度基本没有影响，且该区域与粮堆平均温度的温差在允许的范围内，故对粮食品质不会产生明显影响。相对于垂直地槽通风来说，横向通风不会出现通风死角，通风降温的均匀性大大提高，总体上降温效果优于垂直通风。

(2)横向通风的空气区域存在涡流，所以温度降低较快且梯度较小，在通风第7天时空气区域温差为1℃；垂直通风的空气区域存在较大的温度梯度，在通风第7天时空气区域温差为3.5℃，且粮仓内最高温度在空气区域中下部。

(3)当装粮高度为20 m时，横向与垂直通风的通风阻力都约为1 600 Pa。当装粮高度为30 m时，横向通风阻力为1 614.96 Pa，垂直通风的通风阻力是横向通风阻力的2倍，其值为3 409.74 Pa。可以看出横向通风的通风阻力受装粮高度影响较小，同时当装粮高度较高时，横向通风通风阻力就会有明显优势。