基于高频数据阈值协整模型的上证50股指期货期现套利研究

陈有为 冯楠

摘 要：以上证50股指期货IH1508合约价格序列和上证50指数序列及二者基差序列的1分钟高频数据为例，进行实证分析。首先通过对IF150合约和上证50指数两个时间序列的对数化处理检验确定二者的协整关系，然后采用chow检验二者构建的阈值协整模型，并用Harson格子搜索法估计模型，从而确定期现无套利区间，根据阈值大小区间特性分析套利时机，为中小投资者盈收和规避期货交易风险提供客观决策依据。

关键词：高频数据;股指期货;期现套利;阈值协整模型

中图分类号：F83      文献标志码：A      文章编号：1673-291X（2019）14-0118-02

引言

资本市场在我国近几年的发展日益加速，为了使中小投资者合理规避风险，我国上海期货交易所推出了沪深300指数期货、上证50股指期货等。股指期货在这几年的发展中，资金规模不断扩大，交易量、成交量数据不断上升，市场流动性也逐渐提高。由于市场不够成熟，就提供了很多新的套利机会，因此，对这一方面的研究在理论与实践上都十分必要。

从以前的研究来看，由于国外金融市场发展较早，所以相关的研究比较深入和全面，从套利产生的原因、机会到如何操作都有详细的研究，研究方法也较为全面。国内金融市场起步较晚、起点较低，推出股指期货也不过5年多时间，研究成果多为持有成本理论基础上发展起来的套利方法。由于市场不完善，存在一系列缺点，如理论假设严格、开平仓标准不明确及股息率不确定等，使套利模型主观判断性太强，不利于控制风险。因此，本文研究一种市场中性策略方法，将阈值协整模型应用到上证50股指期货期限套利中，即不论大盘处于何种状态，只要模型出现机会，就可以进行套利操作。

一、数据准备

实证研究采用的是IH1508（期货价格）和上证50指数（现货价格）每1分钟的高频数据，选取的期间为2015年6月23日到2015年8月10日共8 301对数据，现货价格记为xt，上期货价格记为yt，数据均来自于wind资讯。我们分别对IF150合约和上证50指数两个时间序列，基于1分钟高频数据研究序列进行对数化处理，以降低价格序列的异方差性，并将上证50股指期货的对数价格记为Yt，上证50指数的对数价格记为Xt。在每个交易日时间段的选择上，IH1508交易时间是上午9：15—11：30和下午13：00—15：15，而上证50指数的交易时间为上午9：30—11：30（9：00开始集合竞价，半个小时的集合竞价时间，9：30开始2个小时为连续竞价）和下午1：00—3：00。为了便于数据的处理，剔除交易时间不重叠的部分，即剔除9：15—9：30和15：00—15：15时间段内股指期货的价格数据，所以实证分析的时间段为上午9：30—11：30和下午13：00—15：00，样本数据单位为1分钟的高频数据。

二、实证分析

本文实证运用EVIEWS软件可绘制出上证50股指期貨和指数现货两个价格序列走势特征，以及计算出基差的均值、方差、偏度等基本统计特征值。从我国上证50股指期货、现货价格和二者基差1分钟高频数据的价格走势考量，现货和期货价格的整体趋势是下降的，且二者的波动方向大体一致，有较高的相关性。而基差大多分布在（-80，-40）范围内，且基差向下波动的幅度比向上波动的次数和幅度更大，说明在此研究区间正向套利机会有可能偏多。

（一）单位根检验

在对Yt、Xt对数时间序列变量进行实证分析前，需先检验其平稳性。使用Eviews统计软件计算，得到以下对数价格序列的单位根检验，结果显示ADF方法检验P值等于0.225 2，PP方法检验P值为0.253 3，原假设H0不能被拒绝，即上证50现货价格序列存在单位根，该序列是非平稳序列。为了得到Xt序列的单整阶数，我们对该序列的一阶差分进行单位根检验，结果P值均等于0.000 1，则拒绝原假设H0，即该序列一阶差分序列不存在单位根，是平稳序列，说明上证50现货价格序列是一阶单整，记为Xt～I（1），同理可得Yt～I（1）。

（二）最小二乘估计

以Yt作为被解释变量，Xt作为解释变量进行OLS（普通最小二乘法）估计，通过Eviews统计软件计算得到的回归模型为：

Yt=-0.652092+1.080540Xt+Zt（1）

然后对方程1中估计的残差进行单位根检验，若Zt～I（0），则说明Yt和Xt满足协整关系，方程1即是估计的协整方程，从而Yt和Xt的协整关系检验就转化为对残差Zt的单位根检验。从检验结果看，t检验统计量值为-3.582698，小于相应临界值，则说明原假设被拒绝，即残差项不存在单位根，也就是说Zt～I（0）是平稳序列，从而说明Yt和Xt之间存在协整关系，二者相互具有长期均衡关系。

（三）确定滞后阶数

通过R程序中调用软件包tsDyn中的selectSETAR函数运行计算，得出AIC准则下的最佳滞后阶数为14，BIC准则下最佳滞后阶数为5。依据“AIC为主、BIC为辅”的原则，再结合模型显著性进行整体评价，最终确定自回归滞后期为14。

（四）模型的检验

阈值协整模型的检验方法有多种，本文采用chow检验来判断方法。Chow检验法分三个基本步骤：（1）先将资料按照阈值分成三个子样本;（2）提出原假设H0：没有阈值存在和备则假设H1：至少有一阈值存在;（3）若原假设成立则构造F检验统计量：

公式（2）中，SSE表示总样本估计的回归残差平方和，SSE1、SSE2与SSE3分别为三个子样本的回归残差平方和，T为样本量，k为子样本中估计参数的个数，本文实证取k=1。已知，T=830 1，k=1，经计算SSE=2.616 262，SSE1=0.075 023，SSE2=0.174 411，SSE3=0.081 240，得F=286 77.502 9，拒绝原假设，即有阈值存在，证明和之间存在阈值协整关系。

三、閾值和协整向量的估计结果分析

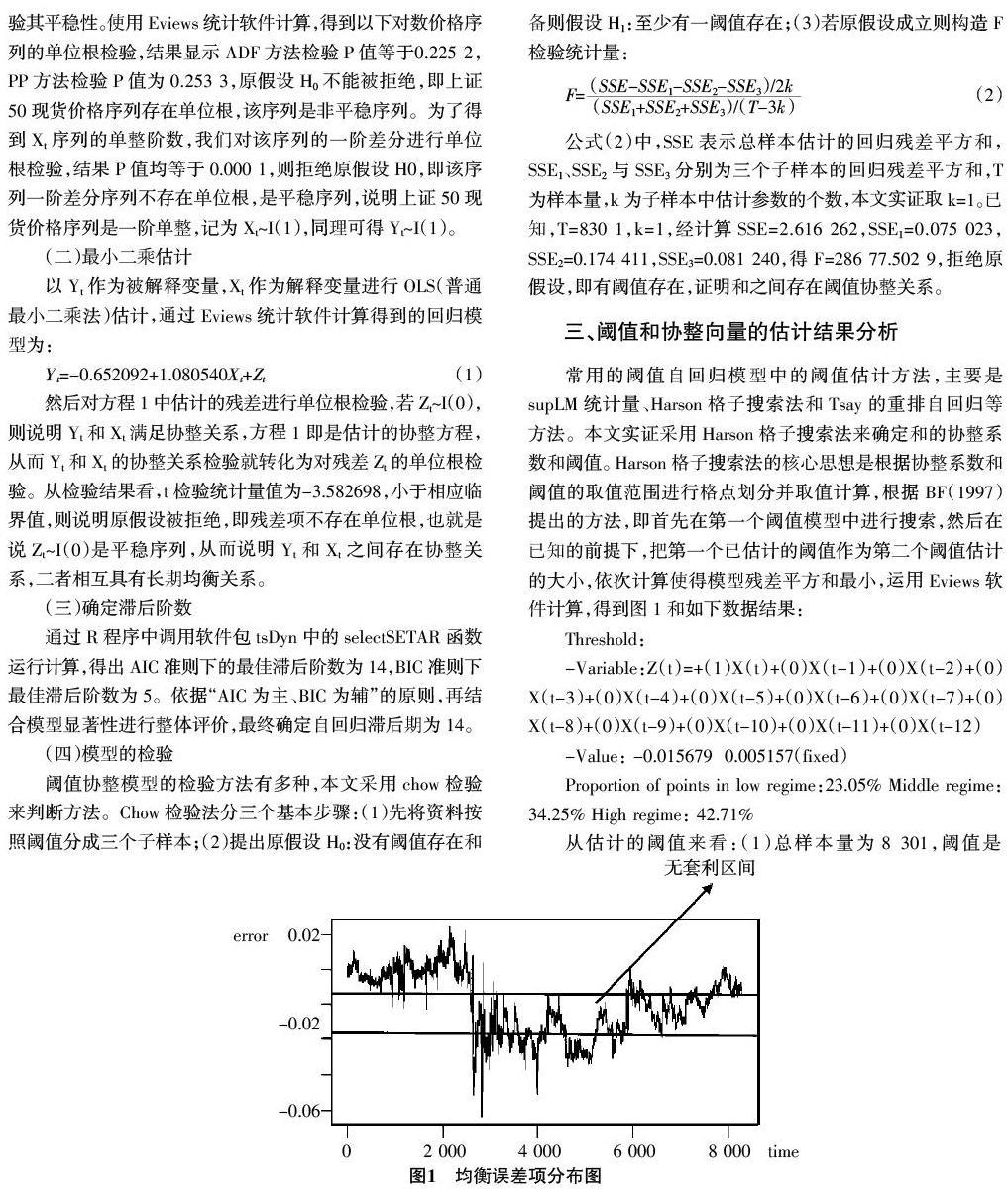
常用的阈值自回归模型中的阈值估计方法，主要是supLM统计量、Harson格子搜索法和Tsay的重排自回归等方法。本文实证采用Harson格子搜索法来确定和的协整系数和阈值。Harson格子搜索法的核心思想是根据协整系数和阈值的取值范围进行格点划分并取值计算，根据BF（1997）提出的方法，即首先在第一个阈值模型中进行搜索，然后在已知的前提下，把第一个已估计的阈值作为第二个阈值估计的大小，依次计算使得模型残差平方和最小，运用Eviews软件计算，得到图1和如下数据结果：

Threshold：

-Variable：Z（t）=+（1）X（t）+（0）X（t-1）+（0）X（t-2）+（0）X（t-3）+（0）X（t-4）+（0）X（t-5）+（0）X（t-6）+（0）X（t-7）+（0）X（t-8）+（0）X（t-9）+（0）X（t-10）+（0）X（t-11）+（0）X（t-12）

-Value： -0.015679  0.005157（fixed）

Proportion of points in low regime：23.05% Middle regime： 34.25% High regime： 42.71%

从估计的阈值来看：（1）总样本量为8 301，阈值是 -0.015 679和0.005 157。上机制、中间机制和下机制样本量分别占总样本量的23.05%、34.25%和42.17%。因此，剔除中间机制，理论套利机会占比总样本量是65.22%。由于23.05%<42.17%，因此负向套利机会大于正向套利机会。（2）两个阈值的绝对值不相等，由于负阀值较小，考虑到我国期货市场规则，沽空现货买入股指期货的套利成本较高，难以大规模套利盈利。（3）两个阈值构成的（-0.015 679，0.005 157）区间是无套利区间，一旦价格偏差低于-0.015 679或高于0.005 157时，即进入可套利交易时机。从估计的自回归系数来看，以1%、10%和5%的显著性水平考量，在中间机制，基差的一阶自回归系数、四阶自回归系数和五阶自回归系数都呈显著性表现，也再次证明（-0.015 679，0.005 157）区间是无套利区间，没有套利机会。

四、结论

本文提出的阈值协整模型相对于论述较多的持有成本理论套利模型，是一种新的研究视角。综合上述实证分析和研究，我们可以看出基于阈值协整模型的期现套利可以应用在我国金融期货市场中。通过模型结果得出期现套利的机会还是比较多的，也从这个侧面间接证明了当前我国的期货市场还是个弱有效市场，比较有利于实施量化套利交易。

参考文献：

[1]  贾雪飞.基于多维协整的统计套利模型研究[D].广州：华南理工大学，2016.

[2]  欧阳红兵，李进.基于协整技术配对交易策略的最优阈值研究[J].投资研究，2015，（11）：79-90.

[3]  戴进.基于协整的股指期货和 ETF 的统计套利[J].中国证券期货，2012，（10）：1-2.

[4]  赵莹，关于中国股指期货的相关问题研究[J].南开大学学报，2012，（6）.

[5]  张连华.基于高频数据的股指期货期现统计套利程序交易[J].计算机应用与软件，2011，（9）：93-95，156.

[6]  Henker，T.and M.Martes，Index Futures Arbitrage before and after the Introduction of Sixteenths on the NYSE[J].Journal of Empirical Finance，2005，（12）.