拱梁组合体系拱桥关键节点有限元分析

(福建船政交通职业学院 汽车运用工程系，福建 福州 350007)

钢管混凝土拱梁组合体系拱桥，外部简支内部超静定，具有受力性能好，施工方便，后期维护工作量小，建筑高度小，结构轻盈美观，造价低等特点[1-3]。

但是，拱座节点结构受力复杂，需承受拱肋轴力与弯矩、系梁预应力、端横梁扭矩的共同作用。作为一种钢和混凝土组合结构，采用杆系模型很难模拟这些关键部位受力情况，需采用实体模型分析应力分布情况，为结构设计和优化提供参考。詹刚毅[4]、张洪金[5]、闫广鹏[6]、魏俊锋[7]分别对拱脚节点的受力性能进行了分析，提出了优化建议。周萌[8]、Ren[9]、Nie[10]、Bai[11]对拱脚节点建模方法提出了参考意见。

本文以某主跨85 m钢管混凝土拱桥为研究对象，采用ANSYS建立局部精细化模型，对拱座进行受力分析。并验证了工程设计的合理性，为同类工程提供参考。

1 工程概述

某大桥主桥上部为下承式钢管混凝土系杆拱，计算跨径85 m，矢高17 m，拱肋轴线为二次抛物线。总体布置如图1所示。

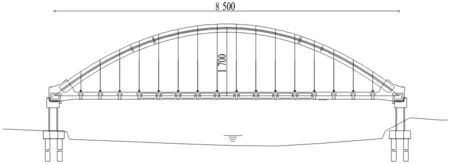
图1 总体布置图(单位：cm)Fig.1 General layout of the whole bridge (unit: cm)

主拱拱肋采用钢管混凝土哑铃型结构，截面宽0.85 m，高2.1 m。钢管直径850 mm，壁厚14 mm，上下钢管中心距1.25 m；腹板厚14 mm，间距0.45 m。拱肋截面构造如图2，其中拱脚段腹腔灌注C50微膨胀混凝土，其余腹腔采用I45a号工字钢对钢板加劲。两拱肋中心距为11.7 m，共设置5道“一字型”风撑。

桥墩采用双柱式墩，桩基采用10根φ120 cm钻孔灌注嵌岩桩。

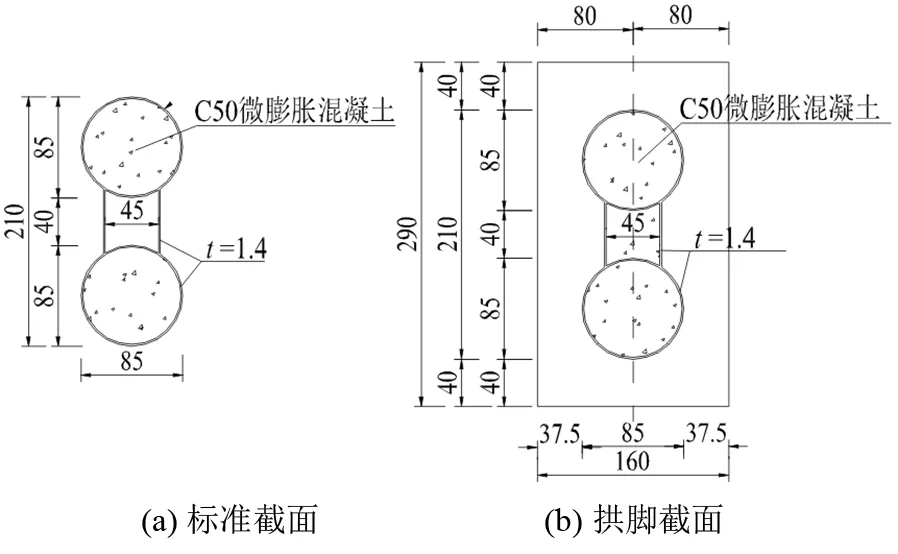
图2 拱肋截面构造图(单位：cm)Fig.2 Structure of arch rib section (unit: cm)

2 结构建模及整体分析

采用MIDAS/Civil有限元软件建立空间杆系模型。其中拱肋、横撑、斜撑、系梁、横梁和桥面板均采用梁单元模拟，桁架单元用来模拟吊杆和系杆。模型如图3所示。

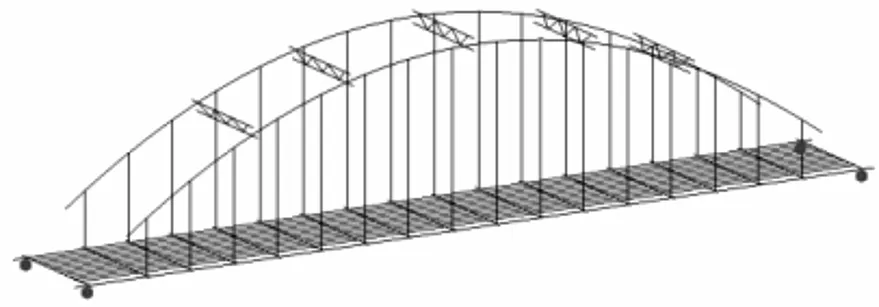
图3 MIDAS/Civil全桥模型Fig.3 Finite element model by MIDAS/Civil

根据《公路桥梁设计通用规范》，取最不利荷载组合：1.0自重+1.0预应力+1.0收缩徐变+1.0汽车荷载(含冲击)+1.0整体升降温+1.0温度梯度，汽车荷载为公路I级。拱肋核心混凝土采用的徐变系数模式按《公路钢筋混凝土及预应力混凝土桥涵设计规范》规定，计算收缩、徐变系数。收缩、徐变的最终时间取成桥后3 650 d。

据当地气象资料，极端最低温度为-7.6 ℃，极端最高温度为39.2 ℃，取两者中间温度15.8 ℃为拱肋浇筑混凝土温度。根据《钢管混凝土拱桥技术规程》第4.2.4条规定合龙温度：

升温温差为39.2-20.3=18.9 ℃，降温温差为20.3+7.6=27.9 ℃。混凝土温度梯度按《公路桥涵设计通用规范》第4.3.10条计算系梁和桥面板升温，日照负温差按正温差的-0.5计算。

3 拱座局部受力分析

3.1 荷载条件

拱座节点局部分析根据设计图纸进行建模，有限元模型包括拱脚伸出2.0 m长的哑铃型拱肋、拱脚实体部分、半跨端横梁(长5.05 m)，如图4。通过分析得到最不利荷载组合下拱脚段截面内力，具体如表1所示，正方向见图4。在拱肋和纵梁各取一个断面用于加载，系杆索力为24 901 kN。按固结方式约束拱脚底部，端横梁限制横桥向位移。

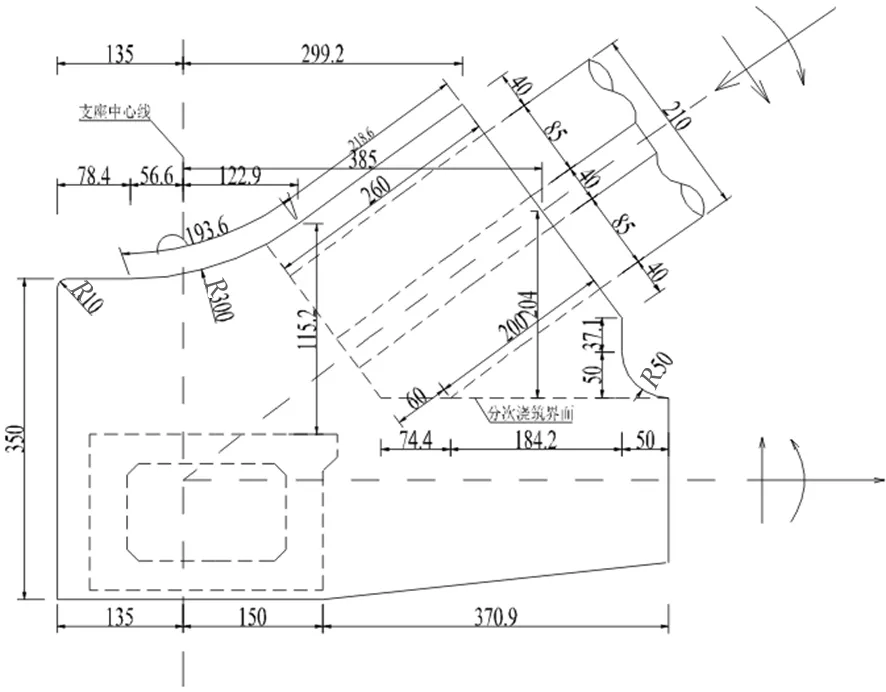
图4 拱座模型的几何尺寸及计算荷载(单位：cm)Fig.4 Geometric dimensions and calculated loads of the arch abutment model(unit: cm)

截面轴力/kN剪力/kN弯矩/(kN·m)拱肋截面15 41641622 422系梁截面11 62270111 622

3.2 有限元模型

采用大型专业程序ANSYS建立拱座节点有限元模型。由于钢管壁厚远小于构件尺寸，比较适合采用板壳单元，因此模型采用四节点壳单元SHELL63进行模拟，弹性模量E=2.06×105MPa，泊松比υ=0.3，钢材密度ρ=7 850 kg/m3。混凝土部分采用实体单元solid95进行分析，钢管内灌注混凝土和拱脚混凝土强度为C50，弹性模量E=3.45×104MPa，泊松比υ=0.17，混凝土密度ρ=2 650 kg/m3。模型按照实际结构尺寸进行建模，根据圣维南原理，主、副拱肋建模长度均为直径的2倍以上。整个有限元模型共65 027个节点，45 504个单元，如图5所示。

图5 有限元计算模型Fig.5 Finite element model

拱肋与拱座绑定，即不允许有相对滑动或分离，可以将此区域看做被连接在一起，类似于共结点。拱脚底部为约束端，按固结考虑，端横梁固定横桥向位移。将集中力转化为均布压力，作用于锚垫板施加面荷载模拟系杆和端横梁预应力锚固处的预应力；在拱肋、纵梁加载面的质心位置建立节点，采用刚臂单元与加载面上其他各点连接，以施加轴力、剪力、弯矩等节点荷载。

3.3 计算结果及分析

3.3.1 结构变形

图6给出了有限元模型计算的变形结果，从图中可看出，在拱脚最大利荷载组合工况下，拱座下挠，整体变形量很小，最大变形出现在哑铃型拱肋加载截面下缘，变形值仅为4.3 mm，表明拱座的结构刚度较大。

图6 整体变形图Fig.6 Whole deformation diagram

3.3.2 应力分析

图7给出了拱座节点模型的主应力迹线图，拱座节点受力以受压为主，设计合理；拱座主应力迹线分布较均匀，表明系杆预应力可均匀分布于受力结构中；矢量方向以纵桥向为主，表明结构以纵向受力为主；系杆预应力的主应力迹线形成从拱肋至系杆预应力锚固区主压应力迹线流，方向指向拱肋端部并与拱肋主应力迹线相接，说明水平方向以推力为主，并且由系杆预应力来平衡。

由于弯矩的影响，拱肋下缘主压应力大于上缘，表现为应力迹线更密集。见图7中的A区域；拱肋内力另一部分表现为竖直分力，传递至支座。从主应力迹线图上可见多个方向向下由拱肋传至支座的应力迹线流。在系杆锚固处、端横梁与节点相交处(B、C区域)，应力集中现象明显，应力迹线密集，压应力较大，同时在压区周围出现拉应力区域，即图7中矩形图框内区域。

图7 混凝土主应力迹线图Fig.7 Principal stress trace of the concrete

图8给出了拱座节点纵、横桥向的应力云图。从图中可见，结构受力以纵桥向受压为主，整体应力值为3～5 MPa，在刚度变化或集中力作用区域，拱肋与拱座节点交界面因刚度突变出现了较大的应力变化，存在不大于1 MPa的主拉应力，小于混凝土抗拉设计强度1.83 MPa，满足要求；拱座节点区域横桥向应力值较小，除了端横梁预应力锚固处压应力在10 MPa左右，其他部位应力绝对值在1 MPa以下，均小于混凝土抗压设计强度22.4 MPa，满足要求。

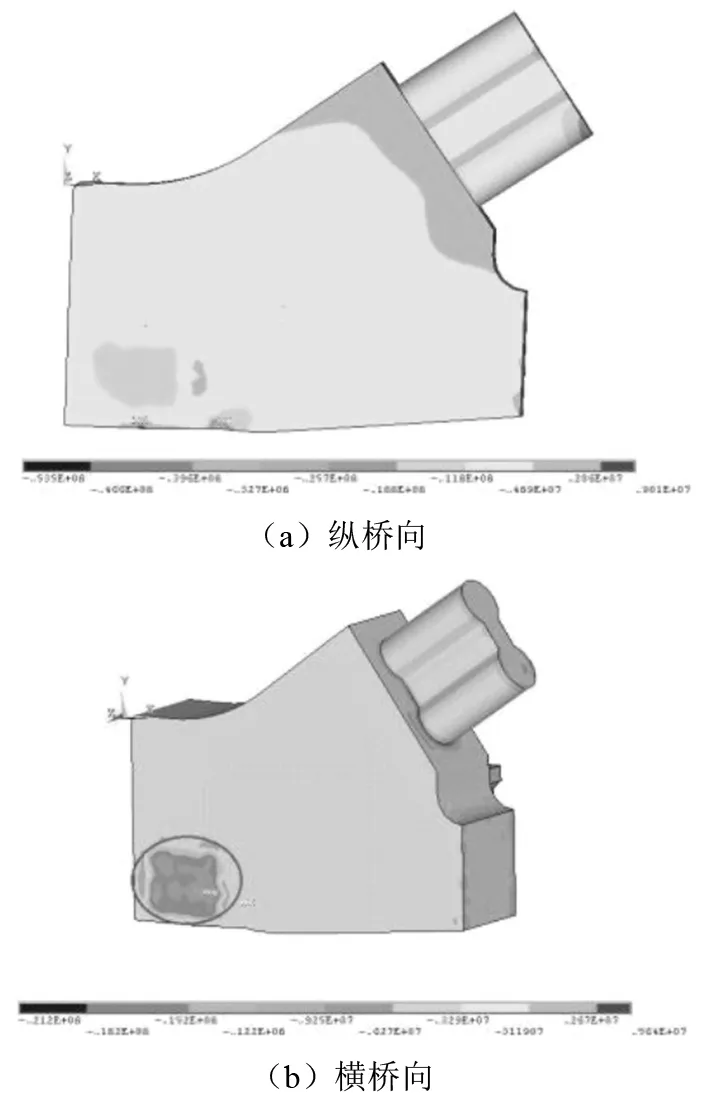
图8 拱座节点应力云图(单位：MPa)Fig.8 Stress nephogram of joints of the arch abutment (unit: MPa)

图9给出了拱座各部位混凝土的主拉应力云图。从图中可以看出，由于拱脚底面固定约束，最大主拉应力出现在约束位置(图9中圆圈处)。拱肋结合面部位、系梁与拱脚结合部位、系梁预应力锚固部位、端横梁预应力锚固部位、端横梁与拱座结合面部位混凝土的主拉应力比较小(基本都小于1 MPa)，小于混凝土抗拉设计强度1.83 MPa，满足要求。

图9 拱座混凝土整体主拉应力云图(单位：MPa)Fig.9 Principal tensile stress nephogram of arch abutment concrete (unit: MPa)

图10、11给出拱座各部位混凝土的主压应力云图。从图中可以看出，除拱肋下弦管下缘应力(因加载端局部受力该截面为加载端局部受力)超过混凝土抗压设计强度22.4 MPa外，其余部分混凝土的主压应力均满足要求。

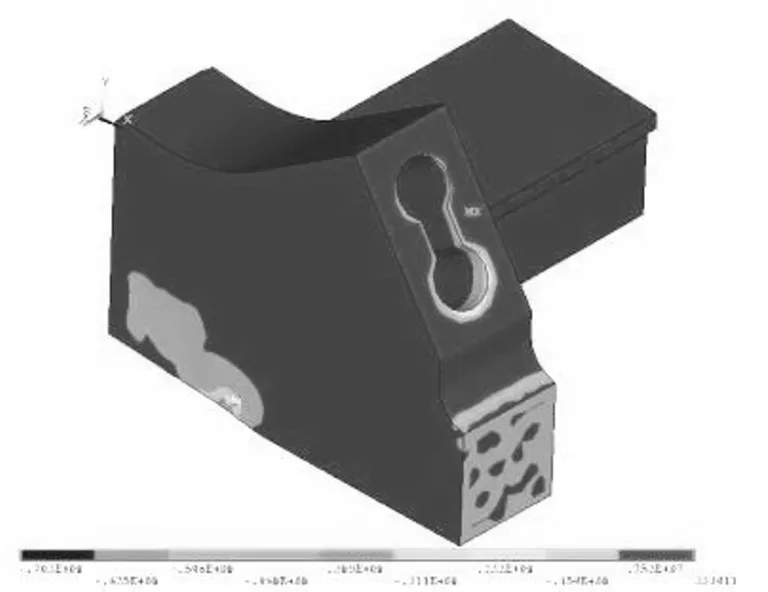
图10 拱座混凝土整体主压应力云图(单位：MPa)Fig.10 Principal compressive stress nephogram of arch abutment concrete (unit: MPa)

图11 钢管内填混凝土主压应力云图(单位：MPa)Fig. 11 Principal compressive stress nephogram of the concrete filled tube (unit: MPa)

图12给出了拱肋弦管与腹板的von-mises应力等效云图，从图中可以看出，最大等效应力出现在拱肋下弦管的下边缘，为94.4 MPa，小于钢材容许应力200 MPa，满足要求。

4 结论

1)拱梁组合体系拱桥拱座的结构刚度比较大，在拱脚最大弯矩工况下，最大变形出现在哑铃型拱肋加载截面下缘，变形值仅为4.3 mm。

2)拱座整体应力分析表明，结构受力以纵桥向受压为主，整体应力值不大，拱肋与拱座节点交界面因刚度突变出现了较大的应力变化，存在不大于1 MPa的主拉应力，满足要求；除了端横梁预应力锚固处压应力在10 MPa左右，其他部位应力绝对值在1 MPa以下，均满足要求。

图12 拱肋von-mises等效应力云图(单位：MPa)Fig.12 Von-mises equivalent stress nephogram of the arch rib (unit: MPa)

3)复杂的空间构造和受力状态使拱座节点容易出现应力集中现象，虽然验算没有超标，但是局部应力高出周围，应在结构中增加加腋、倒角等措施，必要时应增加钢筋用量，进一步优化局部受力。