正方体在立体几何中的模型作用
王建军 郭金红
(1.山西省阳泉市教学研究室 045000;2.山西省阳泉市第二中学校 045000)
基金项目:山西省教育科学“十三五”规划2018年度规划课题《高中数学教学培养学生核心素养的行动研究》(编号GH-18491)(王建军 贾爱寿 田素明 郭金红 梁迎花 李海明等)
正方体是完美的对称图形,是立体几何中的基本模型.正方体中点、线、面之间的位置关系是立体几何的基础,研究正方体中的立体几何问题可以培养学生的空间观念,理解数学的本质,达到快速解题目的.
一、正方体中的平行问题
正方体中平行问题证明的思路具有一般性,是证明直线与平面平行,平面与平面平行的通性通法.
例1如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN,求证:MN∥平面AA1B1B.
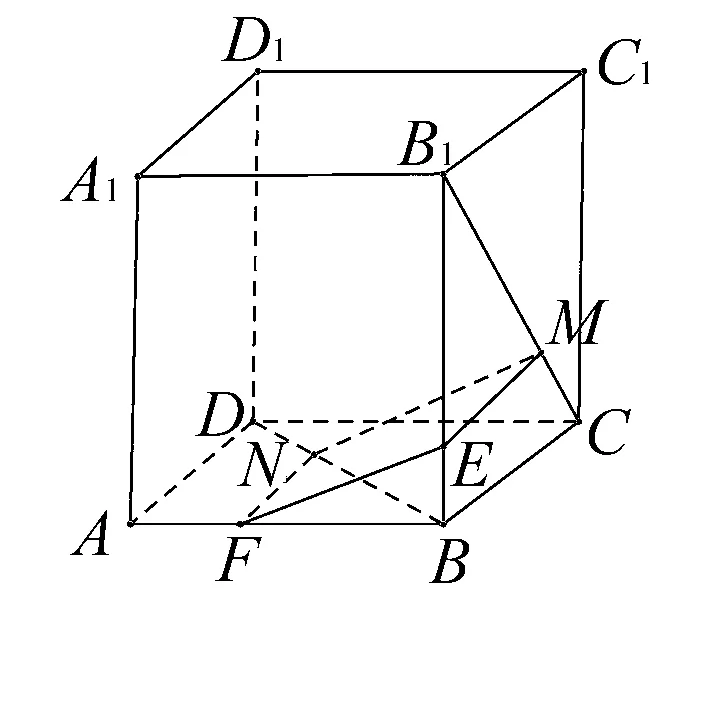
证明如右图,作ME∥BC,交BB1于E;作NF∥AD,交AB于F.连结EF,则EF⊂平面AA1B1B.
∵BD=B1C,DN=CM,∴B1M=BN.

又ME∥NF,∴MEFN为平行四边形.∴MN∥EF.
又MN⊄平面AA1B1B,EF⊂平面AA1B1B,
∴MN∥平面AA1B1B.
二、正方体中的垂直问题
正方体中隐含着线线,线面,面面的垂直关系,利用三种垂直关系来解题是立体几何垂直问题的基础.

例2如图所示,正方体ABCD-A′B′C′D′的棱长为a,M是AD的中点,N是BD′上一点,且D′N∶NB=1∶2,MC与BD交于P.
(1)求证:NP⊥平面ABCD;(2)求平面PNC与平面CC′D′D所成角的正切值.

∴DP∶PB=MD∶BC=1∶2.又已知D′N∶NB=1∶2,由平行线分线段成比例定理得NP∥DD′.又DD′⊥平面ABCD,∴NP⊥平面ABCD.
(2)∵NP∥DD′∥CC′,∴NP、CC′在同一平面内,CC′为平面NPC与平面CC′D′D所成二面角的棱.
又由CC′⊥平面ABCD,得CC′⊥CD,CC′⊥CM,∴∠MCD为该二面角的平面角.

三、正方体中的角问题
正方体中的异面直线所成的角、线面角、二面角的求解过程是解决其他问题的基础.
例3在棱长为4的正方体ABCD-A1B1C1D1中,点P在棱CC1上,且CC1=4CP.求直线AP与平面BCC1B1所成的角的正切值.
解连结BP.∵AB⊥平面BCC1B1,∴AP与平面BCC1B1所成的角就是∠APB.∵CC1=4CP,CC1=4,∴CP=1.


四、正方体中的距离问题
立体几何中的直线到平面的距离、平面到平面的距离最终要转化为点到平面的距离.
例4 正方体ABCD-A1B1C1D1中,E、F分别是AA1,CC1的中点,若正方体棱长为a,求平面EB1D1与平面FBD间的距离.
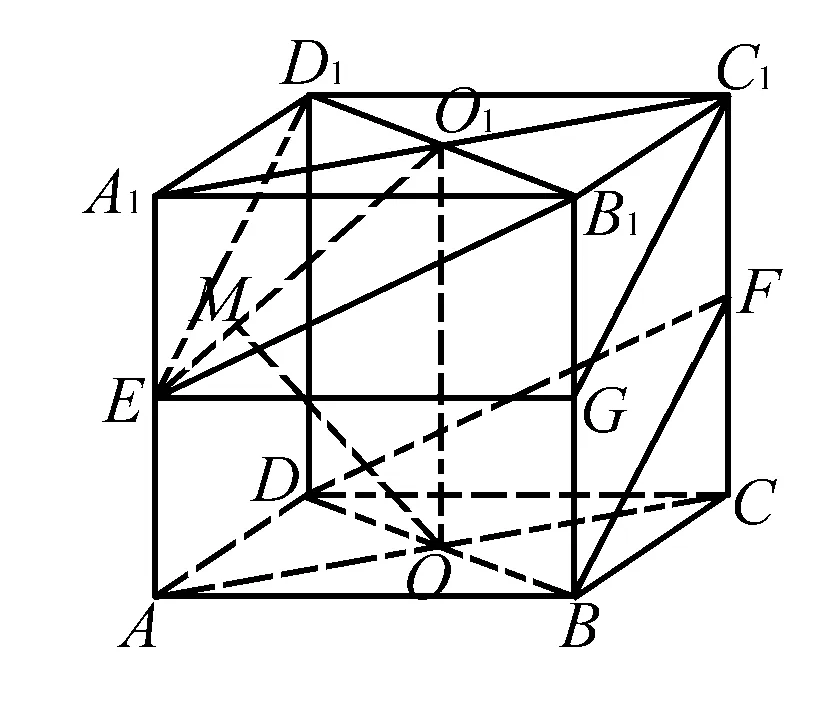
解做BB1的中点G,连接EG,C1G,根据平面几何知识,可得ED1∥GC1,BF∥GC1,∴ED1∥BF, ∵ED1⊄平面FBD,BF⊂平面FBD,∴ED1∥平面FBD.同样,B1D1∥BD, ∵B1D1⊄平面FBD,BD⊂平面FBD,∴B1D1∥平面FBD.
又ED1∩B1D1=D1,∴平面EB1D1∥平面FBD.

连结AC,A1C1,由AC⊥BD,AA1⊥BD,可得BD⊥平面ACC1A1,又BD⊂平面FBD,∴ 平面FBD⊥平面ACC1A1,平面EB1D1⊥平面ACC1A1,连接O1O,O1E,过点O作OM⊥O1E,则OM⊥平面EB1D1,OM即为平面EB1D1与平面FBD


