分离函数法的类型及简单运用
武增明
(云南省玉溪第一中学 653100)

一、把一个函数分离成两个函数的和,求函数的最值(值域)
有些求函数的最值(值域)问题,用常规方法很难求解,甚至几乎解不出来.若想到把一个函数f(x)分离成两个函数g(x)与h(x)的和g(x)+h(x),使两个函数g(x)和h(x)都能判断其单调性,且使两个函数g(x)和h(x)都能在同一处取得最值(极限值),从而问题破解.
例1已知函数f(x)=(2x2-2x-1)ex.
(1)设函数h(x)=exf(x),试讨论函数h(x)的单调性;
(2)设函数T(x)=(x-1)(2xe2x-1)+ex-1-e2x,求函数T(x)的最小值.
解(1)函数h(x)的定义域为(-∞,+∞),h′(x)=4(x2-1)e2x,
当x∈(-∞,-1)时,h′(x)>0,h(x)在(-∞,-1]上为单调增函数;
当x∈(1,+∞)时,h′(x)>0,h(x)在[1,+∞)上为单调增函数;
当x∈(-1,1)时,h′(x)<0,h(x)在[-1,1]上为单调减函数.
于是,函数h(x)在(-∞,-1] ,[1,+∞)上为单调增函数,在[-1,1]上为单调减函数.
(2)函数T(x)=(x-1)(2xe2x-1)+ex-1-e2x=h(x)+ex-1-x+1,
由(1)得,函数h(x)在(-∞,-1] ,[1,+∞)上单增,在[-1,1]上单减,
又x<-1时,h(x)>0,而h(1)=-e2<0,
故函数h(x)的最小值为h(1)=-e2.
令r(x)=ex-1-x+1,则r′(x)=ex-1-1,
当x∈(-∞,1)时,r′(x)<0,r(x)在(-∞,1]上为单调减函数;
当x∈[1,+∞)时,r′(x)>0,r(x)在[1,+∞)上为单调增函数.
所以函数r(x)的最小值为r(1)=1.
故当x=1时,函数T(x)的最小值为1-e2.
评注(1)此题的第(1)问起提示作用,也就是说,如果没有第(1)问,直接求解第(2)问,难度就增加了很多.(2)通过求导来判断函数T(x)的单调性来求其最小值,难度是巨大的,甚至不可能做到.
二、把一个函数分离成两个函数的积,证明函数不等式
有些函数不等式的证明,用常规方法很难奏效,甚至几乎证不出来.若想到把一个函数f(x)分离成两个函数g(x)与h(x)的积g(x)h(x),且使两个函数g(x)和h(x)都能判断其函数值的符号或者单调性,从而可使问题获解.




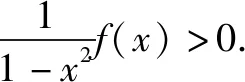
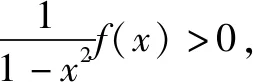
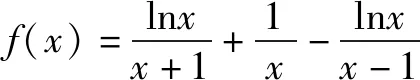
三、把一个函数分离成两个独立的函数,证明函数不等式
有些函数不等式的证明,用常规思维很难证明,甚至几乎行不通.若考虑到把一个函数f(x)分离成两个独立的函数g(x)与h(x),且使两个函数g(x)和h(x)都能判断其单调性,进而分别求出其最值(值域),问题得解.
例3证明:x∈R,a≤1时,xex+a+x2-2x+1>0.
证明要证xex+a+x2-2x+1>0,通过分离函数,即证xex+a>-(x-1)2.
当x>0时,xex+a>0,-(x-1)2≤0,xex+a>-(x-1)2成立.
当x≤0时,f(x)=xex+a的导数f′(x)=(x+1)ex+a,从而f(x)在区间[-1,+∞)上单调递增,在区间(-∞,-1]上单调递减,于是f(x)min=f(-1)=-ea-1.
而g(x)=-(x-1)2(x≤0)的最大值为g(0)=-1.
由于a≤1,有ea-1≤1,且两函数不在同一处取到最值,故x∈R,a≤1时,xex+a>-(x-1)2,即xex+a+x2-2x+1>0.
评注(1)通过求导来求函数F(x)=xex+a+x2-2x+1的单调性,进而求出其最值(值域),是几乎行不通的.(2)要注意“f(x)≥g(x)恒成立”是“f(x)min≥g(x)max”的必要不充分条件.
四、把函数ex和lnx分离开,证明函数不等式
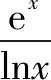

(1)求a,b;
(2)证明:f(x)>1.
分析(1)a=1,b=2(过程略).

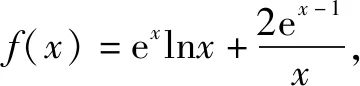
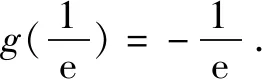

综上,当x>0时,g(x)>h(x),即f(x)>1.

五、分离出
例5(2015年高考全国卷Ⅰ·理12)设函数f(x)=ex(2x-1)-ax+a,其中a<1,若存在唯一的整数x0使得f(x)<0,则a的取值范围是( ).

分析本题若直接求导,就会多次求导后无果;若选择分离参数法,也无法进行下去.我们可以尝试分离出两个常见函数进行求解.
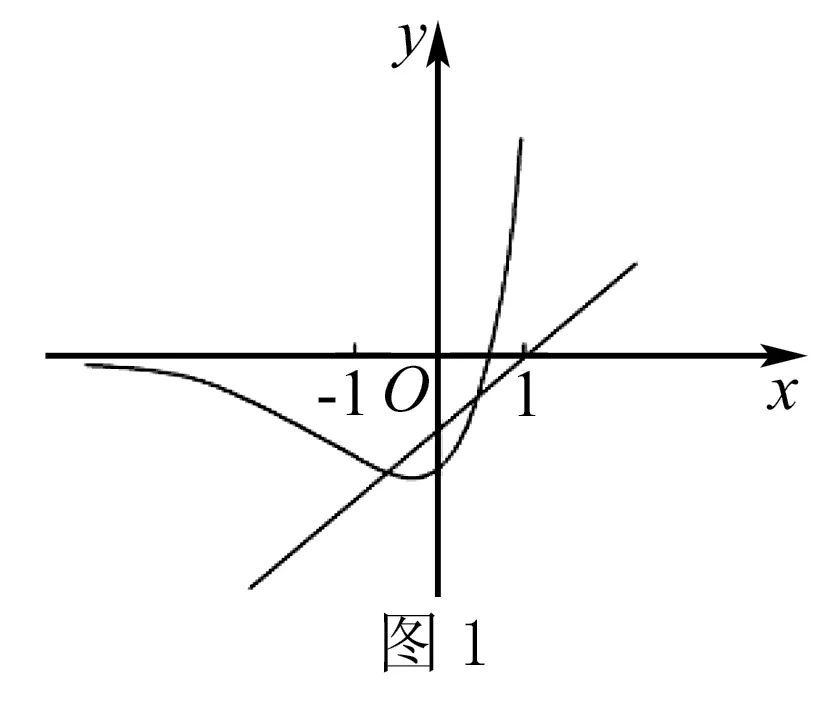
解因为f(x)=ex(2x-1)-ax+a,f(x)<0⟺ex(2x-1) 例6 函数f(x)=lnx-ax2+x有两个零点,则实数a的取值范围是( ). A. (0,1) B. (-∞,1) 分析本题直接求导不好求解,而用分离参数法则比较复杂,小题大做.若将f(x)=lnx-ax2+x=0分离成lnx=ax2-x,利用图象来研究,也很难解释清楚.有没有更好的解法呢? 画出y=g(x)与y=h(x)的图象,如图2所示,可知当a=1时,y=h(x)与y=g(x)相切.当0 从2010年起,高考数学对分离函数法有了明显的关注,导向清晰,而且近几年高考中分离函数法的类型有了新的变化,我们应该加强对此模块的解法研究.分离参数法也是分离函数法,只不过分离参数法中的一个函数是常函数而已.为了让学生更好地理解并应用分离函数法,在教学中,教师应让学生熟知以下函数的图象(如图3).
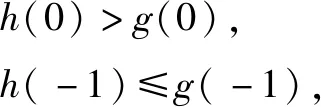

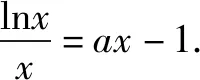

六、反思


