数学中的“转化”之美
温和群
(河北省沧州市第一中学 061000)
一、函数导数的证明问题
函数导数的证明问题是高中数学中的重点难点问题,通常在高考中以压轴题的形式给出,很多学生面对此类问题通常是束手无策.而且此类问题变化多样,证明时入手的角度很多,正是因为如此灵活所以学生掌握起来比较困难.但是我们还是可以从中摸索出解决问题的一些“路径”,最终将问题转化为数学中最基本、最基础的问题来解决.这些转化的方法、处理的策略让我们充分体会到数学之美.
首先,先尝试将不等式整理转化为f(x)≤0或者f(x)≥0的形式,然后构造函数,去研究函数的最小值或者最大值问题.
其次,若构造的函数不好研究,那就尝试将所证明的不等式进行等价变形,变形之后再重复刚才的工作去尝试证明.
第三,可以尝试将要证明的不等式进行变形,转化为f(x)≤g(x)或者f(x)≥g(x)的形式,然后分别研究不等号两边的两个函数的最值,从而证出不等式成立.
第四,如果这几个办法均不奏效,可以尝试将不等式中的某些项进行适当的放缩,转化为比较简单的不等式,而且放缩是遵循一定的章法,这样会使证明成功的几率大大提高.
二、分别举例进行说明
尝试第一种情况:(将不等式两边的式子移至不等号一边构造函数)


f″(x)=sinx-x≤0,
所以f′(x)单调递减.又f′(0)=0,所以当x<0时f′(x)>0,f(x)单调递增;当x>0时,f′(x)<0,f(x)单调递减.
又f(0)=0,所以f(x)≤0,所以原不等式成立.
题后反思:这种处理方式实质是将不等式的证明问题转化为求解函数的最值问题.
尝试第二种情况:(将不等式恒等变形后移至一边构造函数)
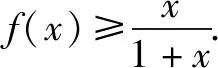

易知:g(x)在(-1,0)上单调递增,在(0,+)上单调递减,所以g(x)max=g(0)=0,所以g(x)≤0
所以1+x≤ex成立,所以原不等式成立.
题后反思:如果直接构造函数,构造的函数很复杂,为后面的研究最值问题带来困难,所以先尝试将要证明的不等式进行恒等变形,转化为比较简单的形式之后再去构造函数,研究最值,显得简洁、睿智.
巩固练习:已知:f(x)=(1+x)e-2x,当x∈[0,1]时,
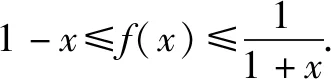
尝试第三种情况:(将不等式的证明转化为f(x)≤k≤g(x)形式的证明问题)



在同一个坐标系中观察两个函数的图象,可以更为清晰地看出两者的关系.

所以原不等式成立.
题后反思:将不等式两边的式子构造为两个函数,分别研究两个函数的性质,发现f(x)max≤f(x0)=k,且g(x)min≥g(x0)=k.将不等式的证明问题转化为求两个函数的最值问题.

∴f′(x)=lnx+1.

又g′(x)=e-x-xe-x=e-x(1-x),可以得出g(x)在x∈(0,1)时单调递增,在x∈(1,+)上单调递减,

在同一个坐标系中观察两个函数的图象,可以更为清晰地看出两者的关系.

所以原不等式成立.
题后反思:将不等式两边的式子构造为两个函数,分别研究两个函数的性质,发现f(x)max≤f(x1)=k,且g(x)min≥g(x2)=k,虽然两个函数的最值不是在同一个x值处取得的,但是最值是相同的,所以仍然可以证得不等式成立.
求证:对任意x>0,g(x)<1+e-2.
尝试第四种情况:将不等式的证明转化为f(x)≤kx+b≤g(x)形式的证明问题
例4(1)求证:(x-1)ex-1>lnx
分析令f(x)=(x-1)ex-1(x>0),g(x)=lnx(x>0).
可以分别证出f(x)>x-1,以及x-1>g(x)两个不等式成立(证明过程略).所以原不等式成立.
这样我们可以在同一个坐标系中作出这四个函数的图象,可以更为清晰地观察这四个函数之间的关系.

题后反思:我们通过分析,不仅证得不等式是成立的,而且可以启发我们以后再证明不等式成立时可以利用(*)式对要证明的不等式进行适当的放缩,使得所要证明的不等式更加简单.
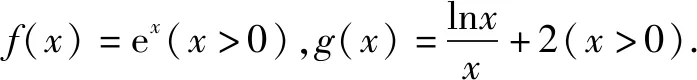
可以分别证出f(x)>x+1,以及x+1>g(x)两个不等式成立(证明过程略).
在同一个坐标系中观察两个函数的图象,可以更为清晰地看出两者的关系.

所以原不等式成立.
题后反思:将一个不等式的证明问题通过等价变形变为去考察“左”“右”两个函数的变化趋势问题,即“分而治之”,利用图象的直观性,可以试图去寻找一条边界线(如切线),这样就可以将不等式的证明问题转化为求两个函数的最值问题,不仅解决了问题,解决问题的思想及图形都给人以美的享受.
不仅如此,利用这些关系进行放缩,大大简化证明问题的难度.
尝试第五种情况:(将不等式中的某些项进行适当的放缩,再进行证明)
例5(1)求证:ex>2x+lnx.
分析考虑将不等式中的ex进行放缩.
因为ex≥x+1,要证原不等式成立,只需要去证x+1>2x+lnx,只需要去证lnx<1-x,令f(x)=lnx-1+x(x<0).
但是经过分析,无法证得f(x)<0,所以放缩失败.
这时考虑另一种放缩:lnx≤x-1,要证原不等式成立,只需要去证x-1
由g′(x)>0,解得0
所以g(x)在x∈(0,ln3)上单调递增;在x∈(ln3,+)上单调递减,所以g(x)max=g(ln3)=3ln3-4=ln27-lne4<0,所以g(x)<0成立,所以原不等式成立.
分析考虑将不等式中的某些项进行放缩.


可以证得f(x)在x∈(0,1)时单调递增,在x∈(1,+)上单调递减,所以f(x)max=f(1)=0.
所以f(x)≤0,所以原不等式成立.
通过这些训练,让同学们去体会:遇到问题不能盲目训练,只是通过加大训练量达到训练目的是很低效的做法,要理清思路,分析和研究问题的特点,抓住问题本质,将问题转化为数学中最基本、最基础的问题来解决.人对美的事物是有追求的,希望我们的学生在研究数学的过程中不仅品尝解题成功带来的喜悦更能体会在解决问题的过程中方法策略的美妙之处.

