驻波声悬浮中对悬浮小物件的操控研究

朱 怡,房 毅

(华东理工大学 理学院,上海 200237)

1866 年，德国科学家Kundt首先发现了谐振管中的声波能够悬浮起灰尘颗粒的实验现象，之后声悬浮逐渐发展为了一项较成熟的技术，由于其能够实现材料的非接触式控制，并对材料的电磁性能没有特殊要求，常常被应用在有机材料的无容器处理，并在医学的“声镊”方向有广阔的发展前景. 实验室中传统的声悬浮演示仪侧重于展示“悬浮”现象，缺少操纵悬浮物的过程[1]. 本文自主搭建声悬浮装置，从单个悬浮物的相对运动和整体运动2个方面，研究驻波声悬浮中对悬浮小物件的操纵实验.

1 声悬浮原理

假定声源的振动方程呈余弦规律变化，则声场空间中的声波的波动方程可写为[2]

y1=Acos (ωt-kz),

(1)

当声波传播至反射面时，将发生反射现象. 声波从波疏介质射向波密介质时的反射过程中，存在半波损失，即在分界面处，反射波与入射波有π的相位突变，反射波的振动方向与入射波的振动相差半个周期. 因此，反射波的波动方程可写为

y2=-Acos (ωt+kz),

(2)

将式(1)和(2)叠加得到在入射波和反射波共同作用下的声场空间中的波动方程，即驻波声场的波动方程为

y=y1+y2=2sin (ωt) sin (kz).

(3)

将式(3)对时间t求导，即可得到媒质质点的速度方程，即

(4)

根据理想流体媒质的3个基本方程中的运动方程可知声场中声压p和质点速度v之间关系[1]，即

v=v0sin (kz)cos (ωt),

(5)

p=-p0cos (kz)sin (ωt),

(6)

式中，v0为媒质质点振动速度的幅值，v0=2Aω；p0为声场中声压幅值，p0=p0cv0.

在声场中空气质点位移较大处为波腹，该点空气质点较疏、声压较小，是声压驻波波节；对空气质点位移较小处的波节，空气质点较密、声压较大，是声压驻波波腹. 声压在刚性平面反射时，在反射面处声压驻波为波腹，图1是声压驻波示意图，线密处表示声压大，线疏处表示声压小.

根据Gor’kov关于声悬浮的理论[5]，作用于半径为R的小球上声辐射时间平均势U为

(7)

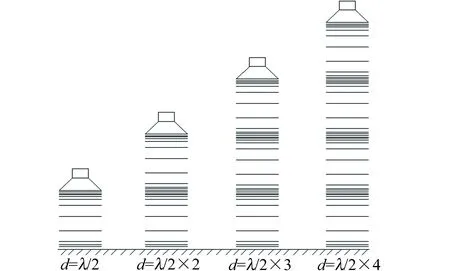
图1 声压驻波示意图

声辐射力为

F=-U.

(8)

物体悬浮在声辐射势的极小值的位置处，在空间形成了势阱. 那么，声辐射力的径向和轴向分量都会表现出回复力的特性，当被悬浮物相对其力平衡位置(稳定悬浮位置)产生微小的偏移时，声辐射力就会使被悬浮物回到原来的平衡位置. 于是，模拟了对应的等效弹簧系统，如图2所示，其中k为弹性系数，则有

图2 等效弹簧系统

(9)

(10)

(11)

由于声辐射力的作用，能使悬浮小球在一定的运动状态下，由声辐射力提供加速度，依然保持悬浮状态，即可以对悬浮小球进行一定的操控.

轴向声悬浮力Fz为

(12)

对于半径为R的悬浮小球，设其密度为ρs，则小球所受到的重力为

(13)

式(12)与式(13)相除可得

(14)

2 实验仪器

驻波声悬浮仪多以单轴式结构为主，图3为其简易示意图. 悬浮装置由超声换能器、变幅杆、发射端以及反射面组成，结构简单，在轴线方向具有较强的悬浮稳定性. 由信号发生器输入超声信号，经过压电陶瓷的转换，由发射端发出超声波，当超声波频率与金属换能器固有频率谐振时，发出的超声信号最强. 当达到发射端与反射端之间的间距H为半波长λ的整数倍时，可以形成驻波.

图3 声悬浮装置示意图

聚焦式声悬浮[6-7]，即将平面反射端改为自制凹面发射端，曲率半径为2.5 cm，凹球面的会聚作用能够提升装置的悬浮性能. 自制聚焦式声悬浮实验装置如图4所示，声悬浮装置和各种悬浮物如图5～6所示.

图4 声悬浮装置实物图

图5 自制聚焦式声悬浮装置

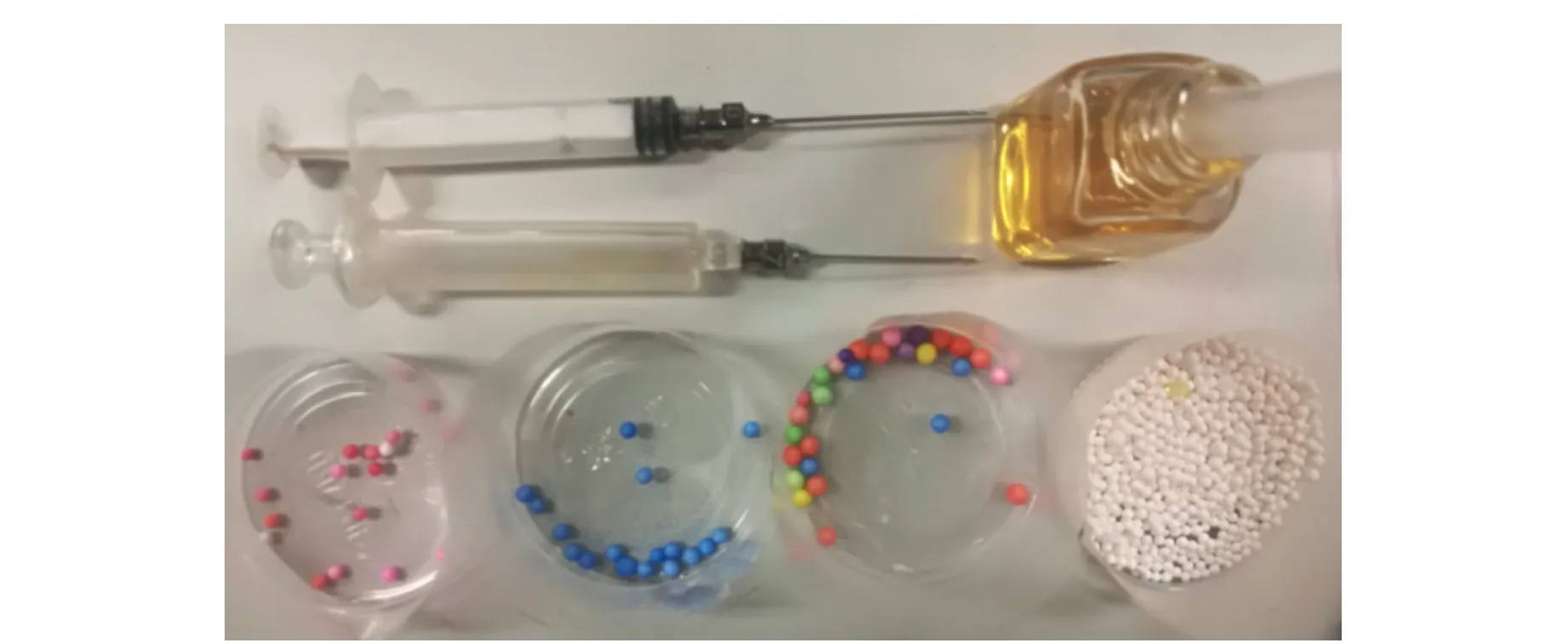
图6 各种悬浮物

3 声悬浮

3.1 验证悬浮条件

采用频率f=37.20 kHz，输入电压U=5 V，室温t=26 ℃，经计算得到声速v=344 m/s. 从零逐渐增大发射端与反射端距离H，当恰好能浮起1～10个小球时，记录其数值. 用Origin软件作出H与n关系如图7所示，得到波长理论值λ=9.247 mm，实验值λ=(9.256±0.011) mm，相对偏差E=0.1%，与理论吻合较好.

图7 H与n关系图

3.2 悬浮小球间隔测量

图8 d与m关系图

3.3 悬浮能力

通过改变超声波频率、输入电压、悬浮物的大小与种类，确定装置的最佳悬浮性能.

1)改变超声波频率

图9 p与f关系图

2)改变输入电压

取f=37.18 kHz，H=4.6 mm，改变输入电压. 同样的方法记录声压值，从图10中得到红线以上的就是悬浮泡沫小球的电压范围为0.5～20.0 V，最佳电压值U>3.5 V.

图10 p与V关系图

3)改变悬浮物的大小

采用最佳的悬浮频率f=37.18 kHz，输入电压U=5 V. 同种材质的泡沫小球，改变小球的半径，测量其最多能悬浮的个数，数据如表1所示，实验照片如图11所示. 由于泡沫是吸声材料，对于声驻波存在一定的影响，且半径越大，对形成稳定的声驻波影响越大.

表1 小球半径与最多能悬浮的个数

(a)1.0 mm (b)1.5 mm (c)2.0 mm图11 不同半径的小球能悬浮的最多个数

4)改变悬浮物种类

对于不同种类的悬浮物，其密度越大，悬浮所需要的声压也越大，如表2所示. 本实验最大能够悬浮起密度为1.9×103kg/m3的氧化铝颗粒.

表2 悬浮物的密度与所需声压

4 仿真模拟

用COMSOL软件模拟驻波声辐射势和粒子轨迹，如图12～13所示，图13中蓝色部分表示声辐射势的极小值，即波节位置，也就是悬浮位置.

图12 模拟声辐射势分布图

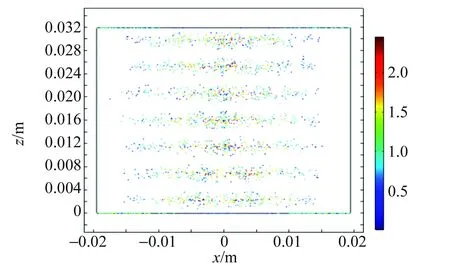
图13 模拟分子轨迹分布图

5 对悬浮物的操作

5.1 单个运动

通过调节超声波的频率和电压实现泡沫小球由静止到自发浮起的变化. 由于势阱的作用，当偏离节点位置释放泡沫小球，在声辐射力的作用下，会将泡沫小球“拉”回节点位置. 最大径向回复距离几乎是整个超声换能面，在2.00 cm左右，轴向回复距离在0.20 cm左右.

通过拍摄慢动作视频，并使用Tracker软件分析小球的运动轨迹，得到小球运动的阻尼曲线，可计算的到x方向和z方向上的回复系数kx=7.34×10-4N/m，kz=16.78×10-4N/m.

5.2 整体运动

将装置放置在转动平台上，改变转速，拍摄视频并用Tracker软件分析，得到整体能达到临界转速为4.36 rad/s，线速度为1.2 m/s.

将超声振子固定在小车并置于倾斜轨道上，使其在轨道上滑动，通过改变轨道倾角来改变小车的加速度. 用光电门测量小车速度，拍摄视频并用Tracker软件分析，得到小球最大加速度为4.39 m/s2，速度为1 m/s，此时轨道倾角为30°.

6 结 论

实验验证了声驻波形成条件，通过改变频率、电压、悬浮物大小和密度，得到装置的最佳悬浮性能：最佳频率值f=37.18 kHz，最佳电压值U>3.5 V，小球的半径越大(不能超过半波长)能悬浮的个数越少，最大能够悬浮起密度为1.9×103kg/m3的氧化铝颗粒. 对于单个悬浮小球的运动，模拟回复系数kx=7.34×10-4N/m，kz=16.78×10-4N/m；保持所有小球悬浮的整体运动，整体临界转速为4.36 rad/s，临界线速度为1.2 m/s；平动的临界加速度为4.39 m/s2，平动的临界速度为1 m/s. 最后用COMSOL软件模拟仿真，进一步分析了小球的悬浮位置的规律性. 本实验装置搭建简单，实验效果明显，利用声悬浮的原理，对悬浮小球进行一定的操纵，具有一定的实际意义.