紫外及深紫外光子晶体微腔特性研究

冯 向，高 娜，b，朱啟芬，黄 凯，康俊勇

(厦门大学 物理系 a.福建省半导体材料及应用重点实验室;b.物理基础教学实验室，福建 厦门 361005)

近年来，光子晶体的研究受到广泛关注[1-3]，光子晶体微腔尤其引起了研究人员的兴趣. 相比于传统的光学谐振腔，光子晶体微腔具有更高的品质因数(Q值)和更小的模式体积，同时若在光子晶体微腔中制造各类“缺陷”，可以精确地调控光子的运动和传播，并可应用于环形谐振腔通道、超快光子晶体微腔激光器和传感器以及滤波器等多种器件[4-7].

1999年，美国加州理工学院O.Painter等首次观测到波长为1.55 μm的光子晶体激光[8]. 2005年，日本京都大学B.S.Song等基于Si材料实现了Q值高达106量级的1.55 μm波长激光出射[9]. 同年，美国加州大学分校Y.S.Choi研究组制备出可见光波段光子晶体激光器[10]. 2006年台湾中央大学L.M.Chang研究组在GaN材料上制作出入射波长短至371 nm的紫外波长光子晶体激光器，但该激光器的Q值较低[11]. 随着微纳米精细加工技术的不断发展[12-14]，制备紫外波段激发波长的小尺寸晶格常量光子晶体微腔已成为可能.

1 原 理

对激发波长位于紫外及深紫外波段的光子晶体微腔特性(例如光子禁带、品质因数等)进行理论模拟，采用平面波展开法(Plane wave expansion method, PWE)[15]和有限时域差分法(Finite difference time domain, FDTD)[16]分析. 首先，将麦克斯韦方程组在坐标系中展开成标量场分量的方程组，然后，将连续的空间和时间离散化，再由数值稳定性条件和计算所考虑的光波长范围确定空间离散步长的大小，并且根据空间离散步长将光子晶体沿坐标轴方向划分若干Yee氏网格单元，得到相应的时间步长，加入边界条件如损耗吸收边界、完全匹配层(PML)等，计算出光子晶体电磁场的分布情况. 其中电磁场满足麦克斯韦方程：

D=εE，

B=μH.

式中，ε为电容率，μ为磁导率，σ和σm分别为介质的电损耗和磁损耗. 该方法下光波能量在微腔中经时间而衰减，通过对时间衰减常量拟合，可进一步根据

获得光子晶体微腔的品质因数Q值. 其中,α为衰减常量，ν为共振频率，α可以通过能量衰减曲线

U(t)=U(0)exp (-αt)

拟合得到. 相较于通常通过获取频率或波长的半高全宽求解Q值的方法，此方法虽然计算速度较慢，但是精确度更高. 在此基础之上，通过自动扫描变量参量，对光子晶体多个微腔结构的填充比等设计参量进行优化.

2 四角晶格纳米微腔的设计与性能预测

2.1 四角晶格纳米孔阵列的光子晶体特性

构造如图1所示的完整四角晶格纳米孔阵列结构，设定AlGaN半导体材料基底的折射率n1=2.5，在其上周期性地形成空气介质(n2=1)纳米孔阵列. 纳米孔洞呈等距间隔的阵列排布，晶格常量a=1 μm，介质孔半径r=0.30a，且选取计算K点路径时，选取相应空间构型二维平面内Γ(四角晶格中心区域)，X(面中心点)和M(垂直棱中心点)3点.

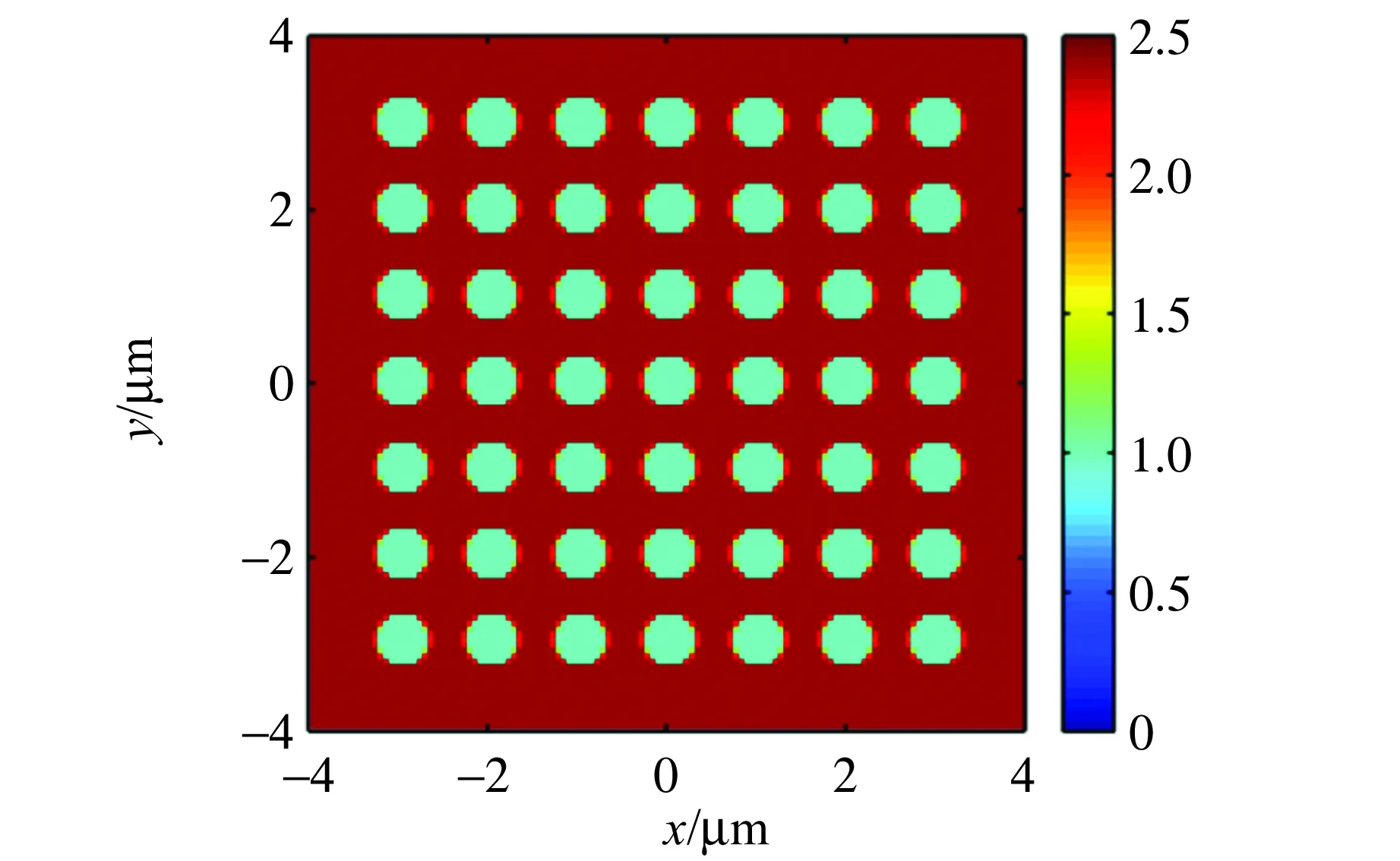
图1 四角晶格模型的折射率分布

采用平面波展开法的计算结果如图2(a)所示，TE模式和TM模式均不存在光子禁带. 在所设结构基底折射率和晶格常量不变的前提下，改变空气介质孔的尺寸. 计算表明，当增大介质孔半径至r=0.42a时，该结构的光子晶体出现TM模式的光子禁带，如图2(b)所示，光子禁带分布在归一化频率0.700 7～0.718 1. 进一步地，逐渐增大介质孔半径至0.44a时，可同时观察到如图2(c)所示的TE模式和TM模式的光子禁带. 然而，由于该结构在2种模式下的光子禁带带宽较窄，并不利于紫外区域光子局域态的形成，有必要进行结构参量的优化.

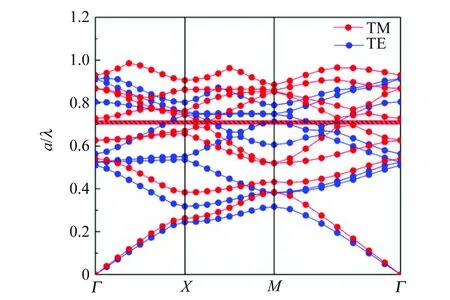
(b)r=0.42a

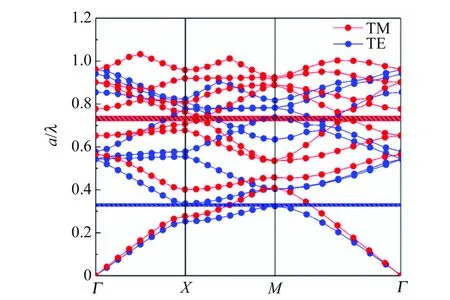
(c)r=0.44a图2 不同介质孔半径的四角晶格 纳米孔阵列的光子能带图

2.2 四角晶格点缺陷光子晶体微腔特性

在上述结构的基础之上，在空气介质孔阵列中央移除1个介质孔单元，以形成点缺陷光子微腔，调控晶格常量a=1 μm，介质孔半径r=0.48a(基底折射率不变). 计算时以FDTD方法的高斯脉冲信号入射，采用PML作为边界条件，获得如图3所示的腔模频谱特性.

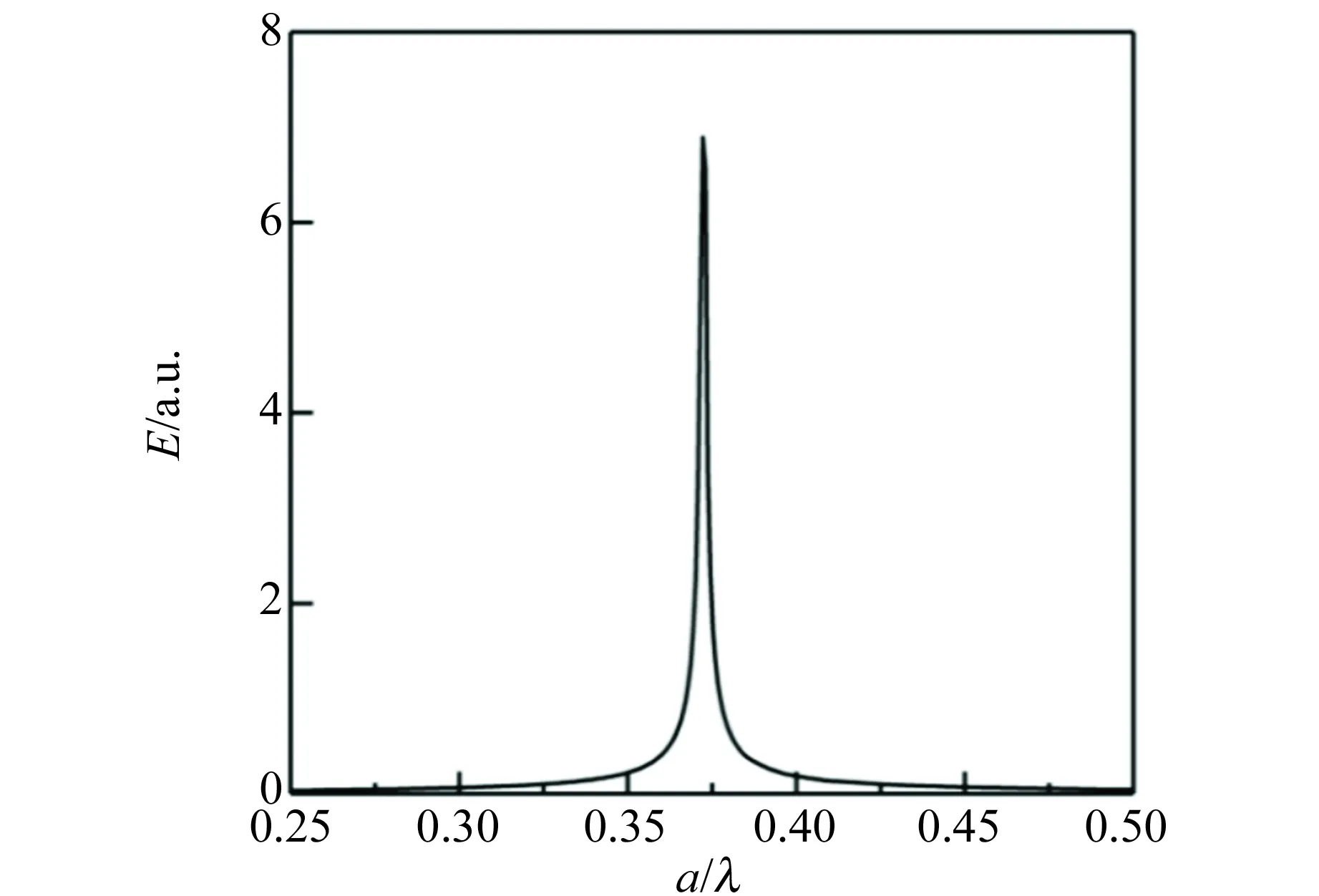
图3 四角晶格点缺陷模型的频谱特性

模拟结果显示，当对应归一化频率为0.372 5的光波入射到谐振腔中时，光波的频率与腔模的频率相吻合，发生相互耦合，使光波被局域在谐振腔内. 进一步地，拟合计算该光子晶体微腔的品质因数Q值为1 914.

从图4的电场分布图可知，尽管入射光波与腔模发生耦合，但二者的耦合共振作用并不强，能量较为分散，导致对光波的局域效果并不理想.

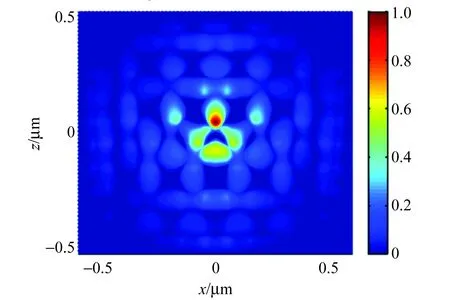
图4 四角晶格点缺陷的电场分布图

为了进一步提高点缺陷光子晶体微腔的品质因子及改善纳米微腔的谐振特性，在不改变基底折射率的情况下，将通过改变光子晶体的结构对称性来降低腔模线宽.

3 六角晶格纳米微腔的设计与性能预测

3.1 六角晶格纳米孔阵列的光子晶体特性

选定结构对称性比较高的六角晶格为单元，在半导体材料基底上构造六角晶格空气介质孔阵，孔半径为0.30a，其中计算K点路径选取空间构型二维平面内Γ(六角晶格中心区域)，M(面中心点)以及K(垂直棱中心点)3点. 模拟结果显示，所设计的光子晶体存在TM模式光子禁带，其归一化频率位于0.297 7～0.361 2范围，如图5所示.

图5 完整的六角晶格光子晶体的能带分布图

相比于四角晶格纳米孔光子晶体出现的光子禁带，六角晶格光子晶体相应光子禁带带隙明显变宽. 也就是说，六角晶格结构更有利于对紫外波段光子能量的局域和限制.

为此，在该结构中引入点缺陷，发现原本较完整的光子禁带分裂为2条宽度相对较窄的光子禁带，如图6所示. 猜测耦合到缺陷模的光子能量会得到显著增强.

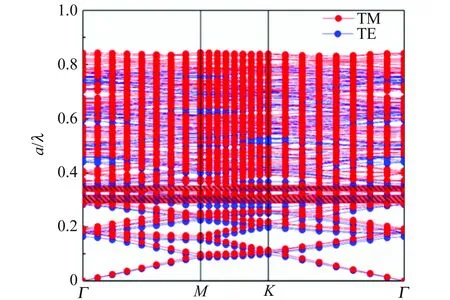
图6 含点缺陷六角晶格光子晶体的能带分布图

3.2 六角晶格点缺陷光子晶体微腔特性及优化

如图7模型所示，对含单个点缺陷的六角晶格光子晶体微腔结构进行模拟.

图7 六角晶格点缺陷模型

以填充因子FF为变量，不难发现，共振频率随着FF的增大而增大，如图8所示，共振波长变化范围为310～240 nm，而且随着频率增大逐渐蓝移.

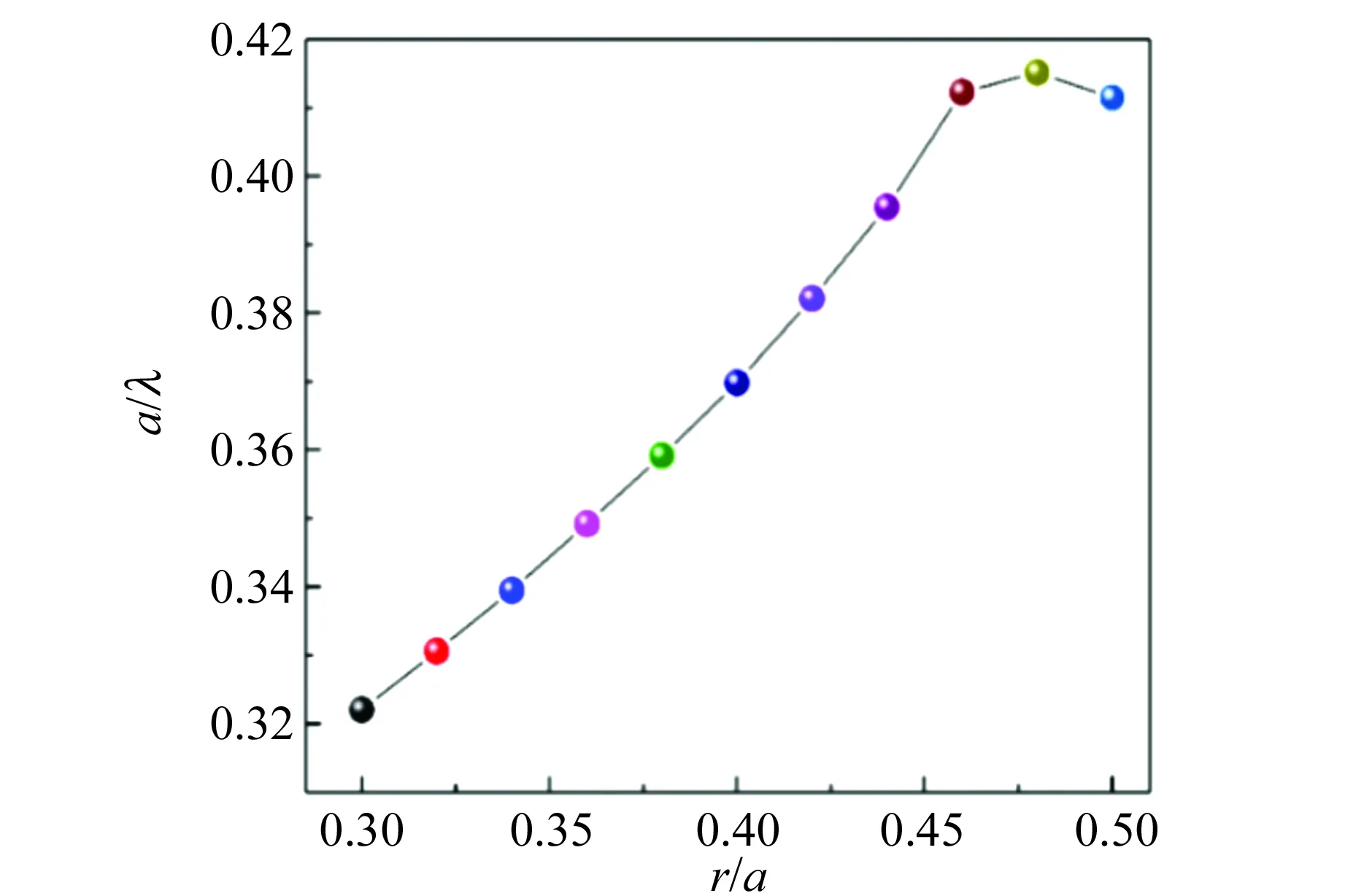
图8 谐振腔共振频率

当FF在0.30～0.50范围内变化时，观察到其品质因数Q值先上升后下降，如图9所示，在r=0.40a附近上升到最高值3 417.

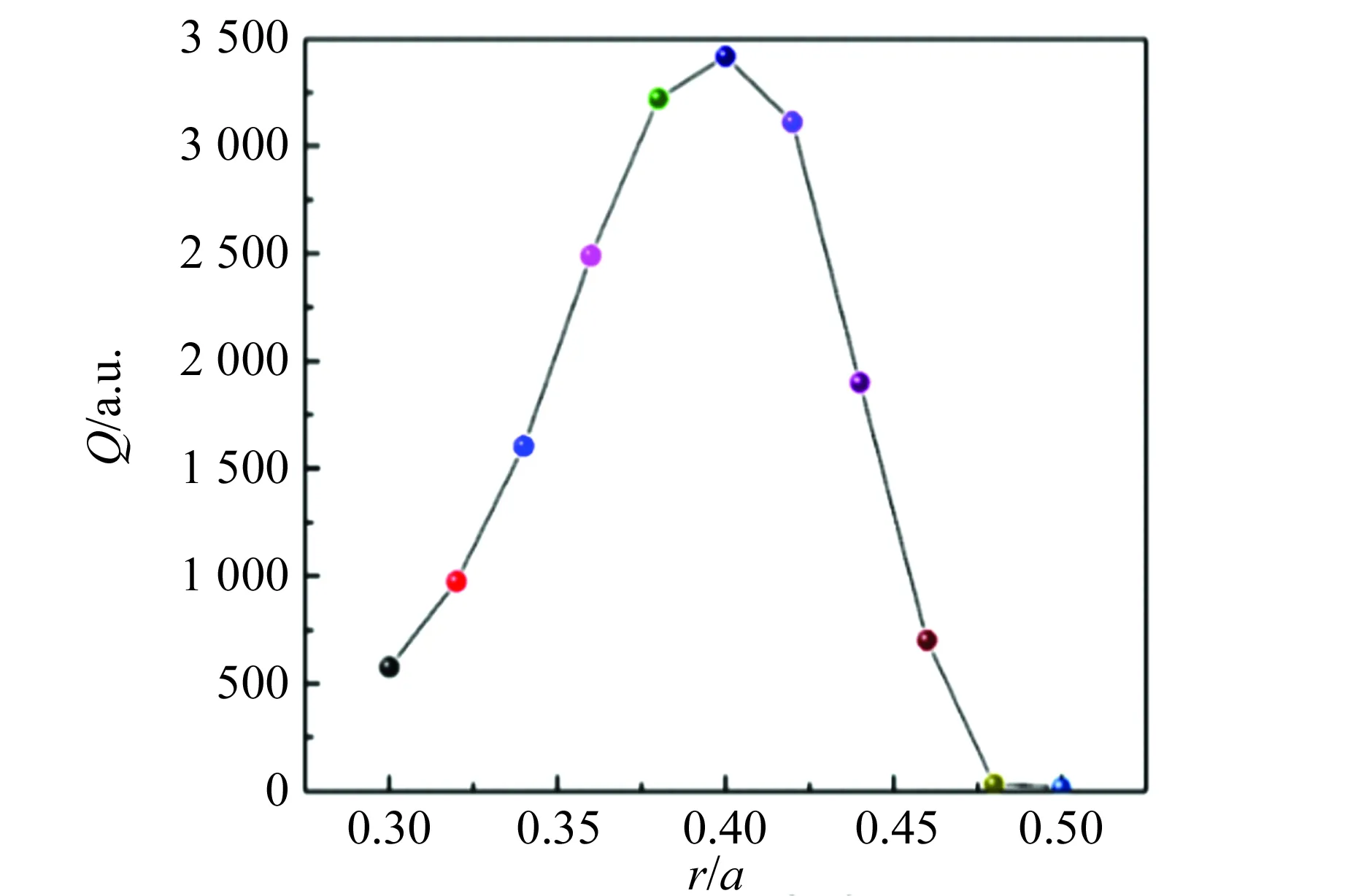
图9 Q值优化曲线

对最高品质因数时的电场进行分析，可知微腔缺陷模与入射光波的耦合恰好局域在中央缺陷处，如图10所示，明显地，缺陷外区域几乎无场强分布，因而微腔缺陷具有显著增强紫外光约束和限制作用.

图10 六角晶格点缺陷模型的电场分布图

考虑到实际样品中存在的缺陷附近孔径会有所变化，因而进一步地，以点缺陷附近6个纳米孔径r2为变量，保持外围r1=0.40a不变，如图11所示，模拟扫描Q值如图12所示.

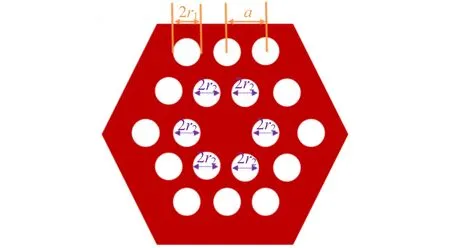
图11 内径优化模型示意图

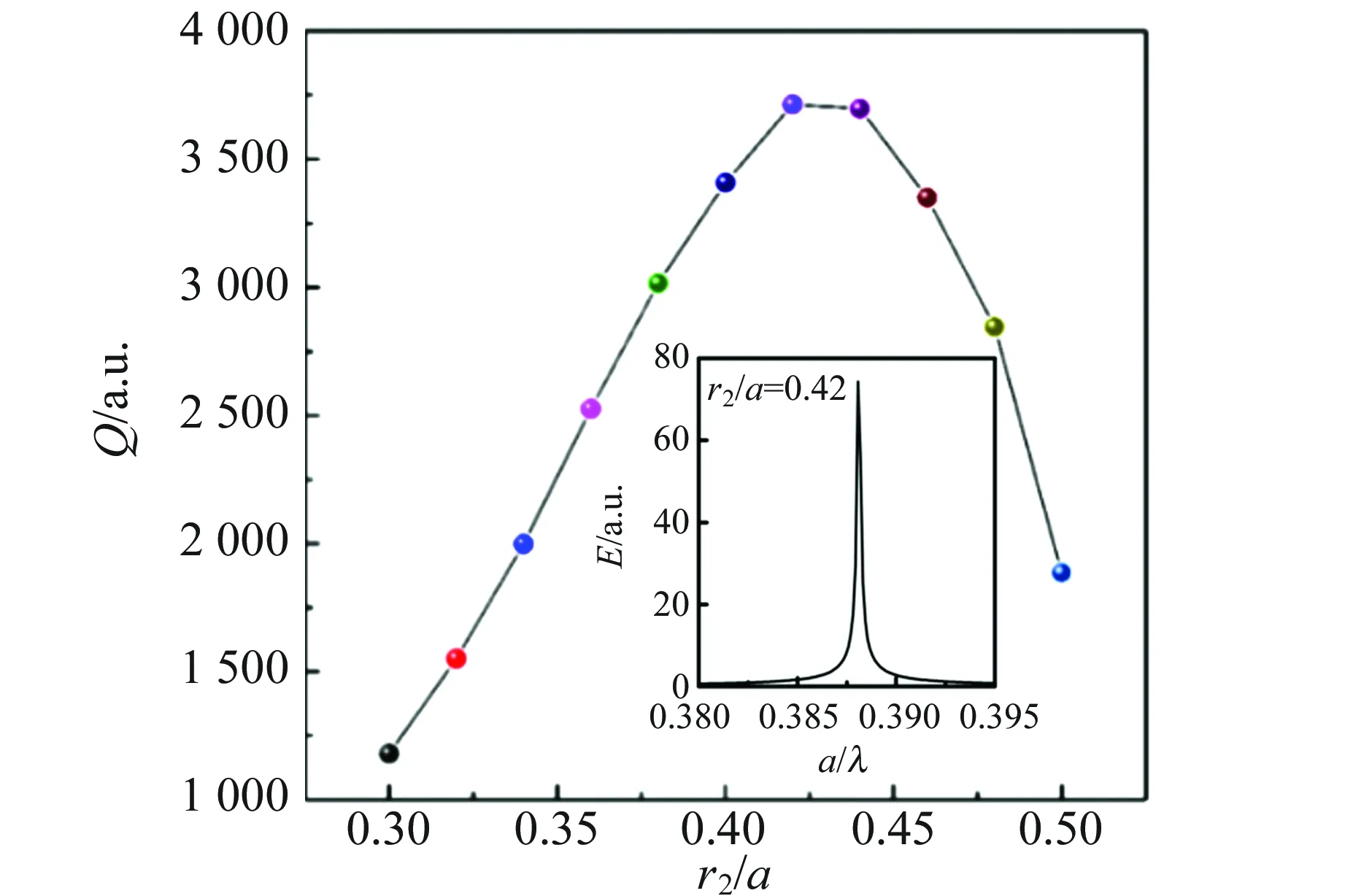
图12 内径优化后Q值变化曲线

当r1=r2=0.40a，与图7中模型一致时，Q值保持3 417不变.当逐渐增大孔径于r2=0.42a处Q值略有提升，此时Q值增大至3 713. 虽然Q值提升幅度并不大，但是相比仅含单个点缺陷的六角晶格光子晶体有所上升. 为此，将对含有多缺陷的六角晶格光子晶体微腔进行结构设计和参量优化.

3.3 六角晶格多缺陷光子晶体微腔特性及优化

明显地，多个点缺陷的光子晶体微腔对光的局域作用更强. 模拟过程中，保持基底折射率不变，以填充因子FF=r/a为变量，扫描范围设定为0.3～0.5. 由于多个点缺陷的腔频谱中存在多个共振峰，因此每次等间隔取点后取品质因数最高的峰，并且获取图13. 从图13中可以看出，当FF=r/a=0.36时，品质因数Q值最高，可以达到6 107.

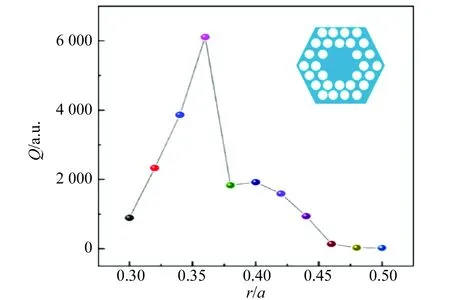
图13 六角晶格多缺陷光子晶体微腔的Q值变化曲线

图14为FF分别为0.36，0.38，0.42，0.44的共振谱线，其中共振峰1和2都来源于缺陷处形成的局域电场，当FF逐渐增大时，二者逐渐向高频方向移动，意味着共振波长向着深紫外波段蓝移.

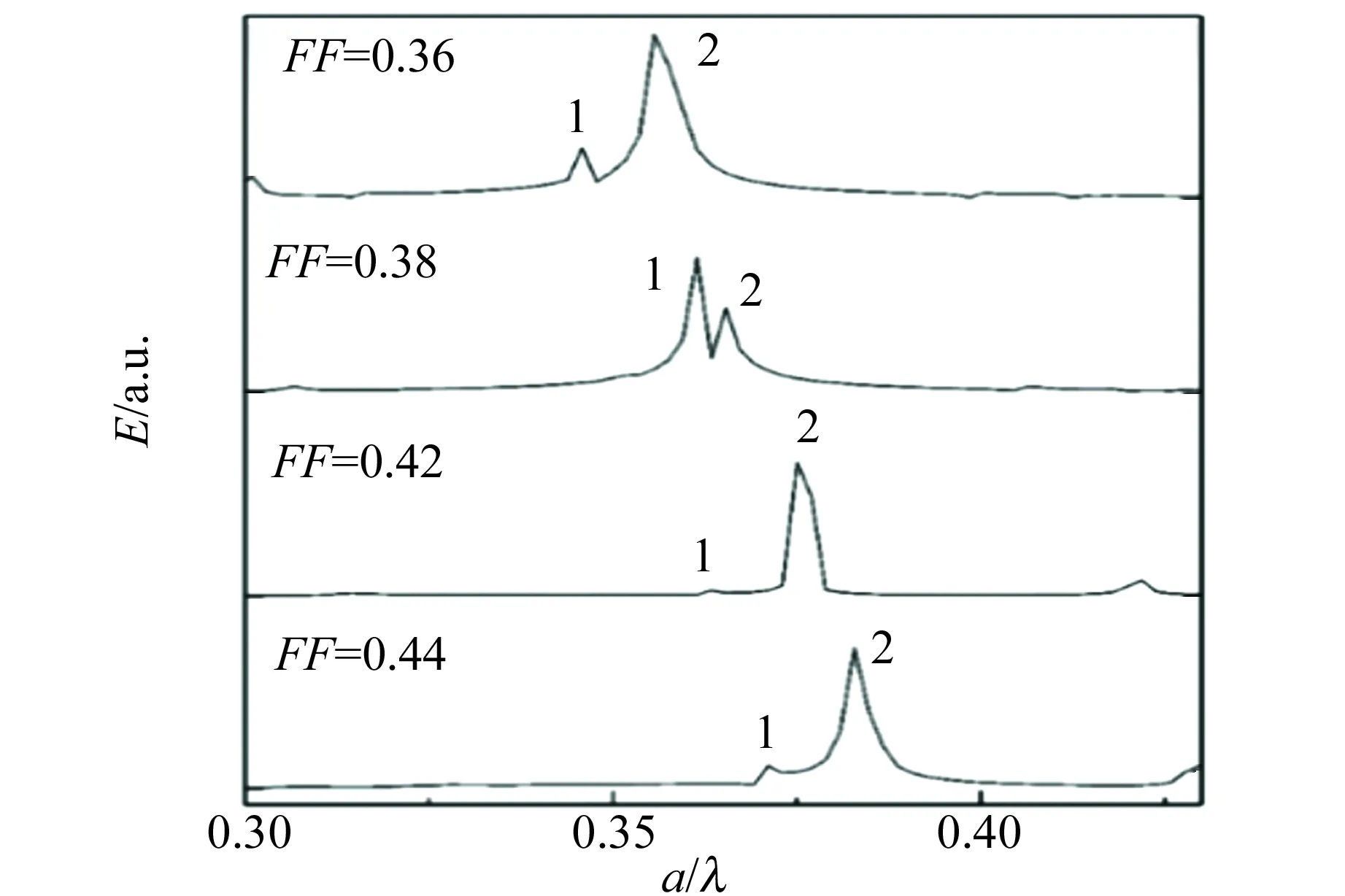
图14 不同填充因子下的谐振腔频谱特性

不难发现，当FF=0.36时，共振峰2的强度明显较高，如图15(a)所示，该共振波长处形成了显著增强的缺陷模局域电场. 当增大FF至0.38时，从图14看共振峰1和峰2的强度差减小，但平均强度较FF=0.36时有所减小，因此其共振强度及品质因数Q值也减小. 进一步增大FF至0.40时，所形成的缺陷模电场分布类似于图15(a)，而且Q值略有提高. 有趣的是，当调控FF为0.44时，此时电场的振荡模式明显发生了变化，但此多模式微腔的Q值并不高. 比较而言，当调控FF为0.36时，所设计的多缺陷光子晶体微腔结构具有最理想的品质因数.

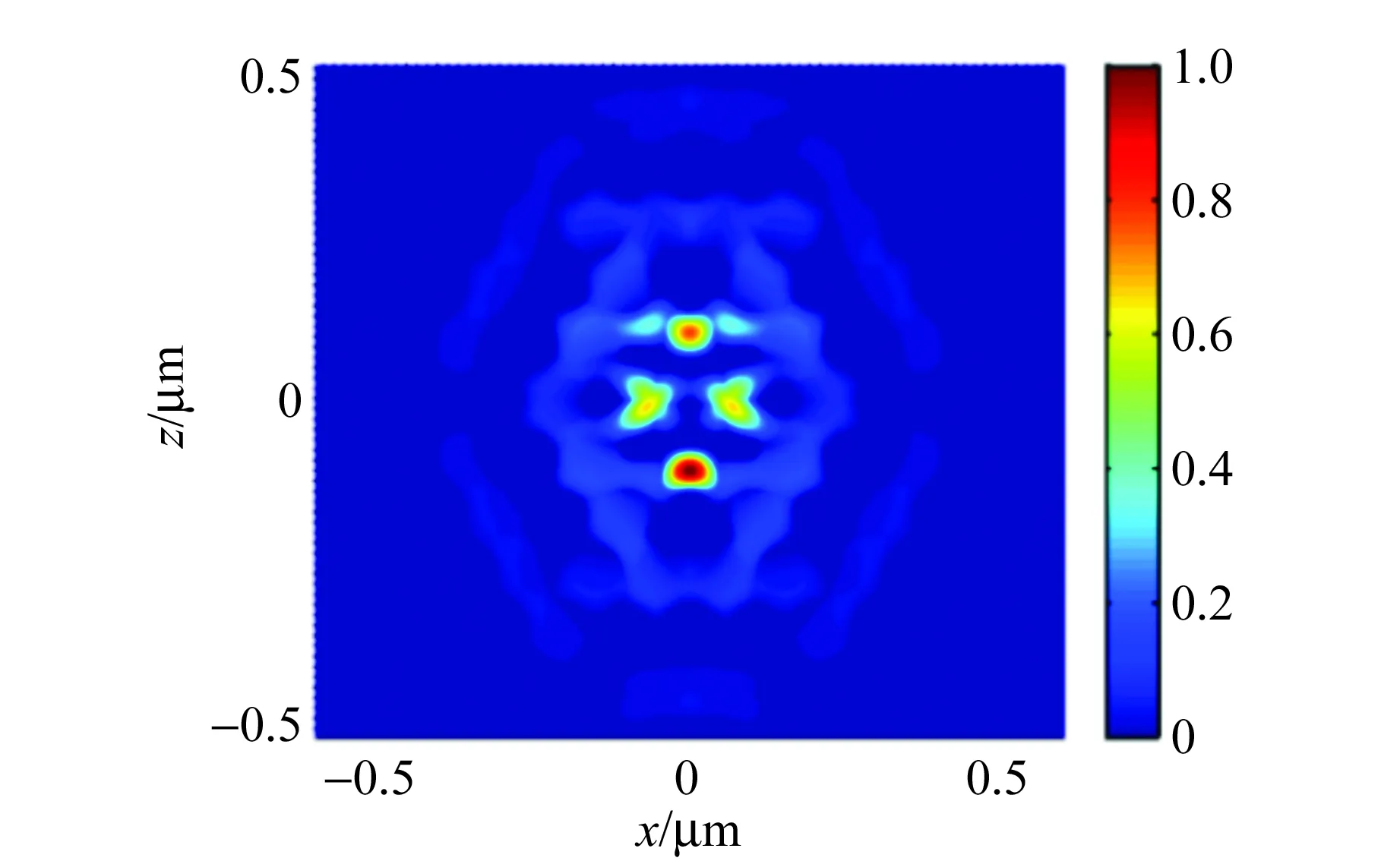
(a)FF=0.30/0.32/0.34/0.36/0.40

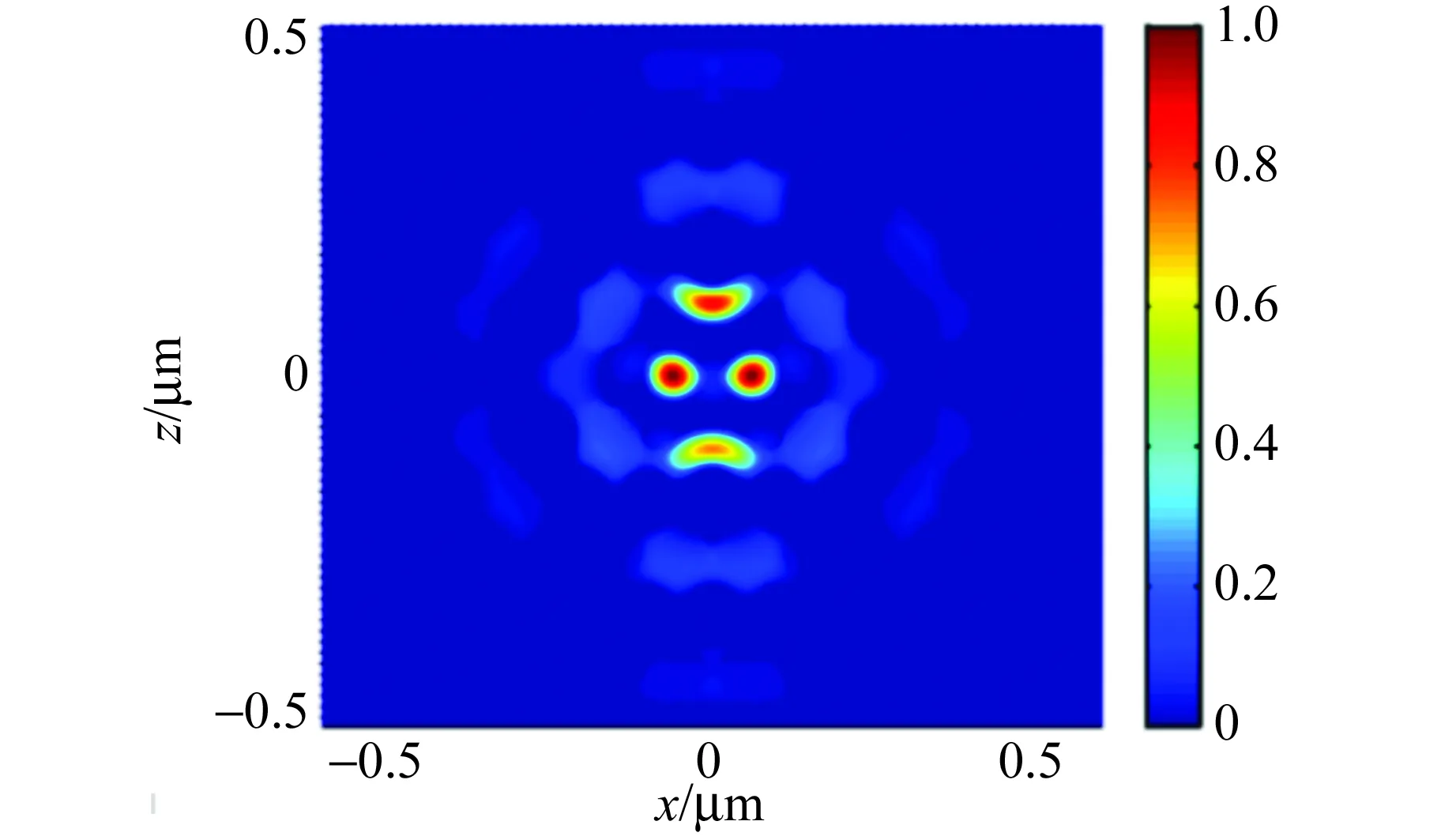
(b)FF=0.38

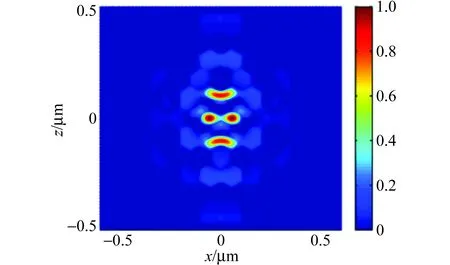
(c)FF=0.42

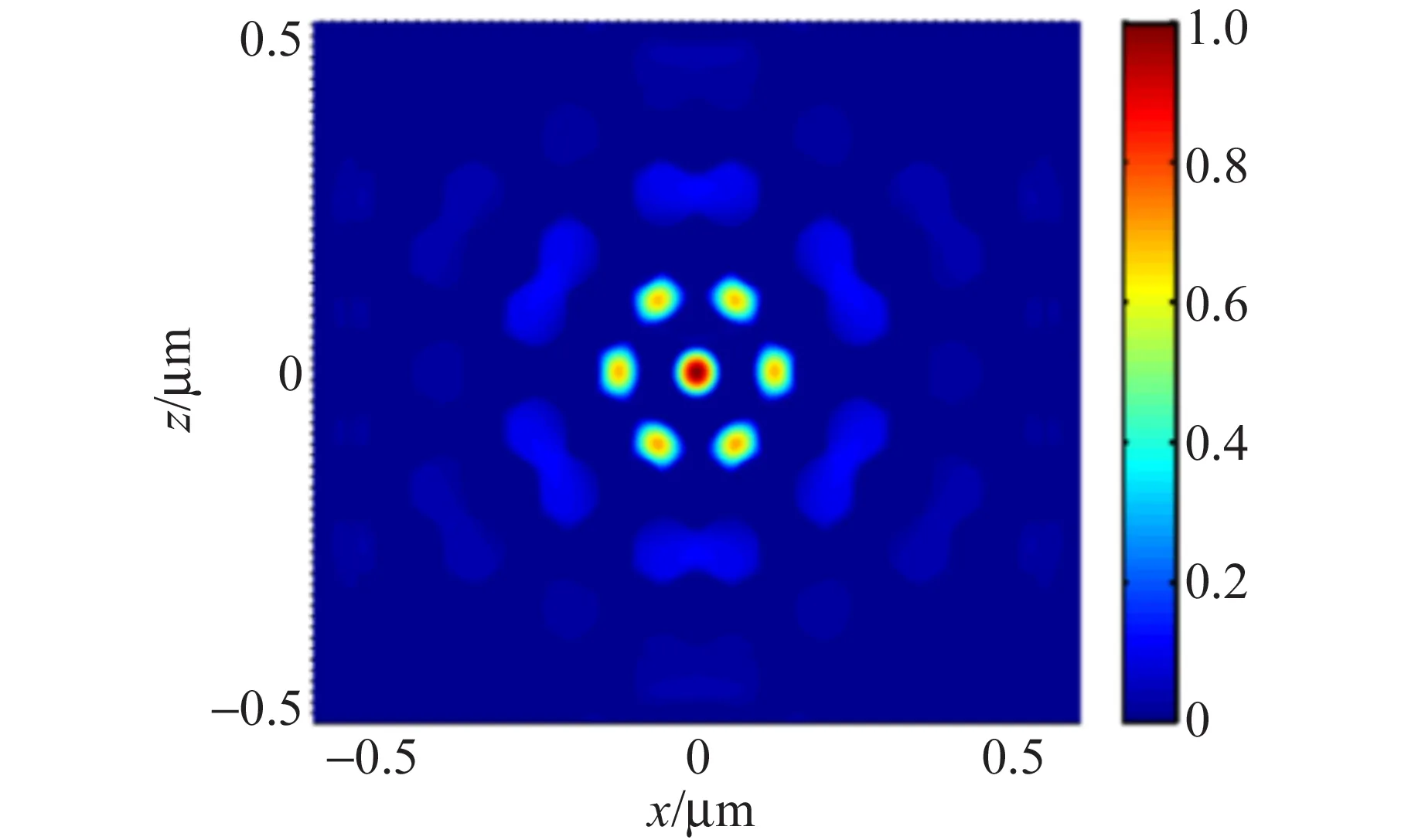
(d)FF=0.44/0.46/0.48/0.50图15 六角晶格多缺陷光子晶体微腔的电场分布

4 结 论

通过平面波展开法结合FDTD法对光子晶体能带以及微腔的品质因数Q值等特性进行仿真计算，并通过改变晶格类型和晶格常量以及缺陷结构优化紫外及深紫外光子晶体微腔的性能. 计算表明，相较于光子禁带较窄的四角晶格光子晶体微腔，在六角晶格结构中引入点缺陷，相当于将可传播模式限制于光子禁带中心，更能增强对紫外光子的局域和限制并获得较高的品质因数. 模拟还发现，随着填充因子的逐渐增大，单个点缺陷微腔的品质因数变化趋势表现为先增大后减小，当填充因子为0.40时达到最高值3 417. 进一步优化点缺陷附近的6个孔内径，发现比单一点缺陷结构的品质因数有所提高. 其中，当填充因子为0.36时，多缺陷的六角晶格光子晶体微腔的品质因数可高达6 107. 因此有望与当前的微纳米精细加工技术结合，设计和制备出紫外及深紫外光子晶体微腔.