基于光学超晶格的新型激光器和新颖光学效应
胡小鹏,张 勇
(南京大学 现代工程与应用科学学院,江苏 南京 210093)
光子和电子都是信息的重要载体. 在半导体材料中,通过对电子能带的设计和剪裁,可以实现电子的调控,这是当代信息技术的基础. 受半导体超晶格概念的启发,南京大学的科研工作者在20世纪80年代初,将微结构引入到介电晶体中,形成了介电体超晶格[1]. 在介电晶体中引入有序结构,可以实现对不同物理常量的有序调控. 对晶体的电容率,或者是折射率进行周期性调制,这是大家熟知的光子晶体,具有光子能带[2-4]. 如果对材料的非线性系数进行调制,则被称为准相位匹配材料. 因为准相位匹配材料在激光的频率转换方面有着广泛而重要的应用,而且其特征尺寸一般在几至几十μm量级,通常又被称为光学超晶格[2-4].
1 光学超晶格基本概念
常用的光学超晶格的基质材料有铌酸锂(LiNbO3,LN)和钽酸锂(LiTaO3,LT)等铁电晶体. 它们具有ABO3的钙钛矿结构,整个晶体可以看成由氧八面体组成,相邻氧八面体有共同的顶点. 在室温下,铌酸锂和钽酸锂都是铁电相,属于3m点群,无对称中心. 在这类铁电晶体中,正负电荷的中心沿着C(z)轴方向分离,因此只存在自发极化反平行的2种铁电畴. 通常把平行于晶体C轴取向的畴称为正畴,反平行的则称为负畴. 将1对正负畴作为基本的构造单元,如果重复排列基本构造单元,则构成了最简单的周期光学超晶格,如图1所示.
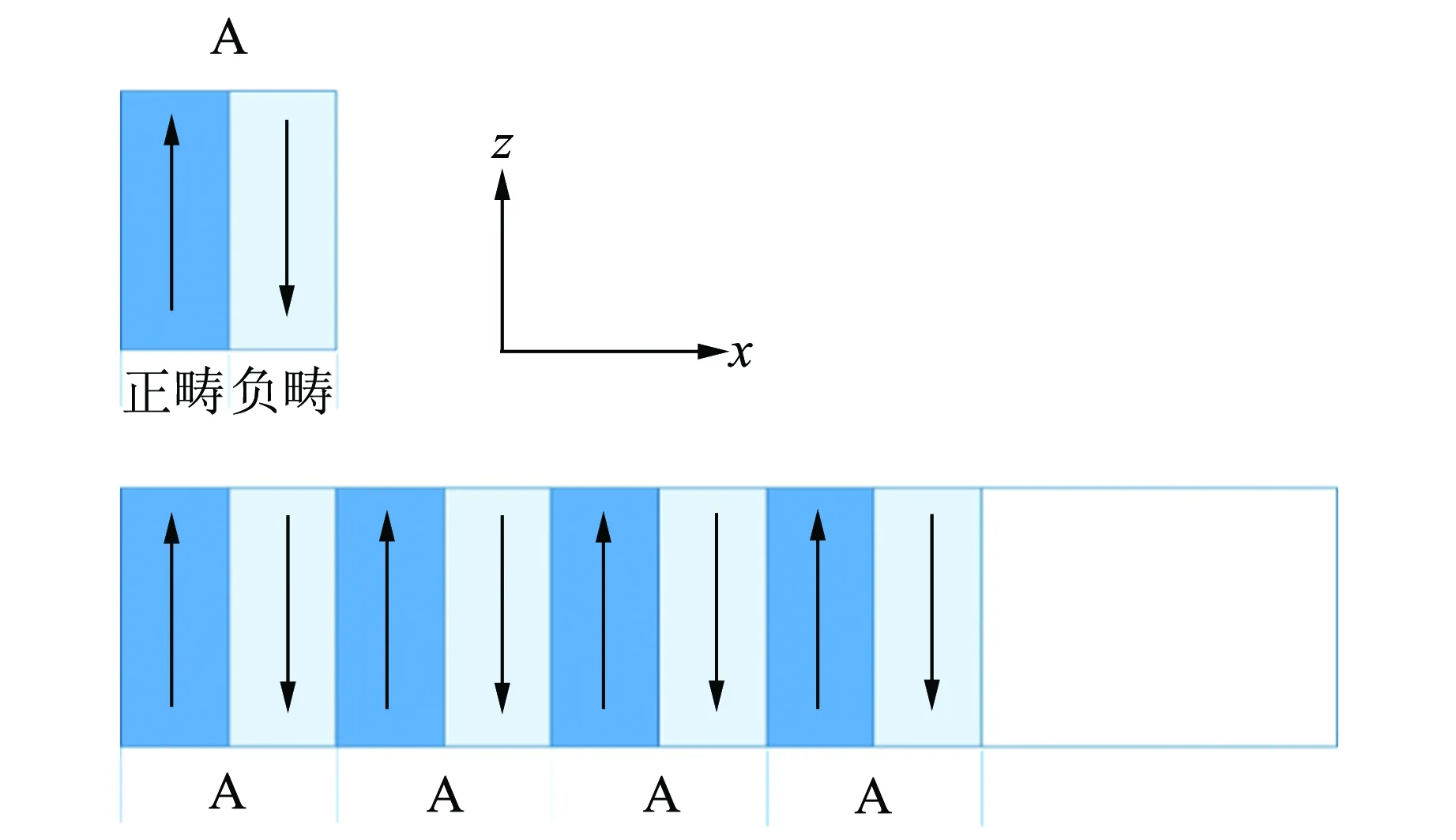
图1 周期结构光学超晶格组成示意图
因为正负畴的自发极化矢量方向相反,相当于2个铁电畴的坐标系统围绕晶体的C轴旋转了180°,因此在这2个铁电畴中,与奇数阶张量相关的物理参量,例如二阶非线性光学系数和电光系数等的符号相反. 也就是说,在正畴中,晶体的最大二阶非线性系数d33取正号,在负畴中d33则取负号. 可以用矩形波函数f(x)来表征超晶格的结构,在正畴中f(x)=+1,在负畴中f(x)=-1. 通过傅里叶展开,光学超晶格中的二阶非线性系数随着位置的变化关系可以写成:
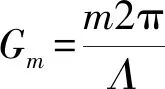
光学超晶格是一种重要的微结构功能材料,在非线性频率转换方面有重要的应用. 对于非线性光学过程,以最简单的倍频过程为例,也就是让频率为ω1=ω的基波光通过二阶非线性过程变为频率为ω2=2ω的倍频光. 要高效地完成这一非线性过程,必须同时满足能量守恒和动量守恒2个条件. 能量守恒条件Δω=ω2-2ω1=0自动满足. 非线性光学过程中的动量守恒又称为相位匹配,对于倍频过程,动量失配
其中,k1和k2分别为基频光和倍频光的波矢,nω和n2ω为对应的折射率,λ为基频光的波长. 由于晶体材料存在色散,倍频过程的动量失配Δk一般不为零. 1961年,Kleinman等人提出了双折射相位匹配(Birefringence phase matching,BPM)[5],让相互作用的光处于不同的偏振态,在某个特定的方向上利用晶体的双折射特性来实现相位匹配. 双折射相位匹配受制于晶体材料的双折射特性,不能让所有波长的光都实现相位匹配;BPM过程使用晶体二阶非线性系数的非对角元,通常数值较小;BPM还存在空间上的走离效应,这就限制了非线性转换的效率. 1962年,诺贝尔奖获得者Bloembergen教授提出了著名的准相位匹配理论(Quasi phase matching, QPM)[6-7],主要通过周期性调制晶体的非线性极化率,在倒空间提供倒格矢Gm来补偿非线性相互作用过程中因为材料色散导致的基频光和倍频光之间的波矢失配,使得Δk=k2-2k1-Gm=0,从而获得高效的非线性频率转换效率. 也可以从实空间来理解准相位匹配. 在正常色散晶体材料中,长波长的基频光的相速度比短波长的倍频光的相速度快,因此产生了2者之间的相位失配,基频光和倍频光之间的能量流动每隔1个相干长度lc=π/Δk就改变1次方向,其振荡周期为2倍的相干长度. 在光学超晶格中,非线性极化率或非线性系数每隔1个相干长度改变符号,即能量流动每隔1个相干长度改变方向,从而保证了能量能从基频光持续地转移至倍频光,实现了高效的倍频转换. 准相位匹配原理如图2所示.
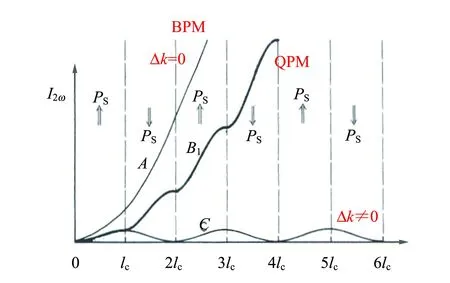
图2 准相位匹配原理示意图
准相位匹配和双折射相位匹配方式相比较,有如下的优点:
1)准相位匹配中相互作用的光处于相同的偏振状态,可以利用晶体的最大二阶非线性系数d33.
2)基频光和谐波光共线发生非线性相互作用,避免了双折射相位匹配中的空间走离问题.
以上2点使得准相位匹配可以获得更加高效的非线性转换效率.
3)准相位匹配不受制于材料的双折射特性,通过超晶格微结构的设计,可以在晶体的透光波段范围内实现任意波长的相位匹配.
目前,周期结构的光学超晶格已被广泛应用激光的倍频、和频、差频和光参量振荡器,实现波段覆盖紫外到中红外的各种高效光源[8].
2 准周期光学超晶格
准相位匹配发展的很长时间内,使用的都是最简单的周期结构. 周期结构只能提供1组倒格矢,高效地完成1个非线性光学过程. 受准晶发现的启示[9],在20世纪80年代后期,南京大学的研究人员将准周期结构引入到光学超晶格的设计中来,提出了多重准相位匹配理论[10]. 一维准周期光学超晶格是由2个或者2个以上的结构单元按照特定的迭代序列拼彻而成. 假设A和B为2个长度不同的结构单元,这2个构造单元均由1对正负畴构成,如图3所示.
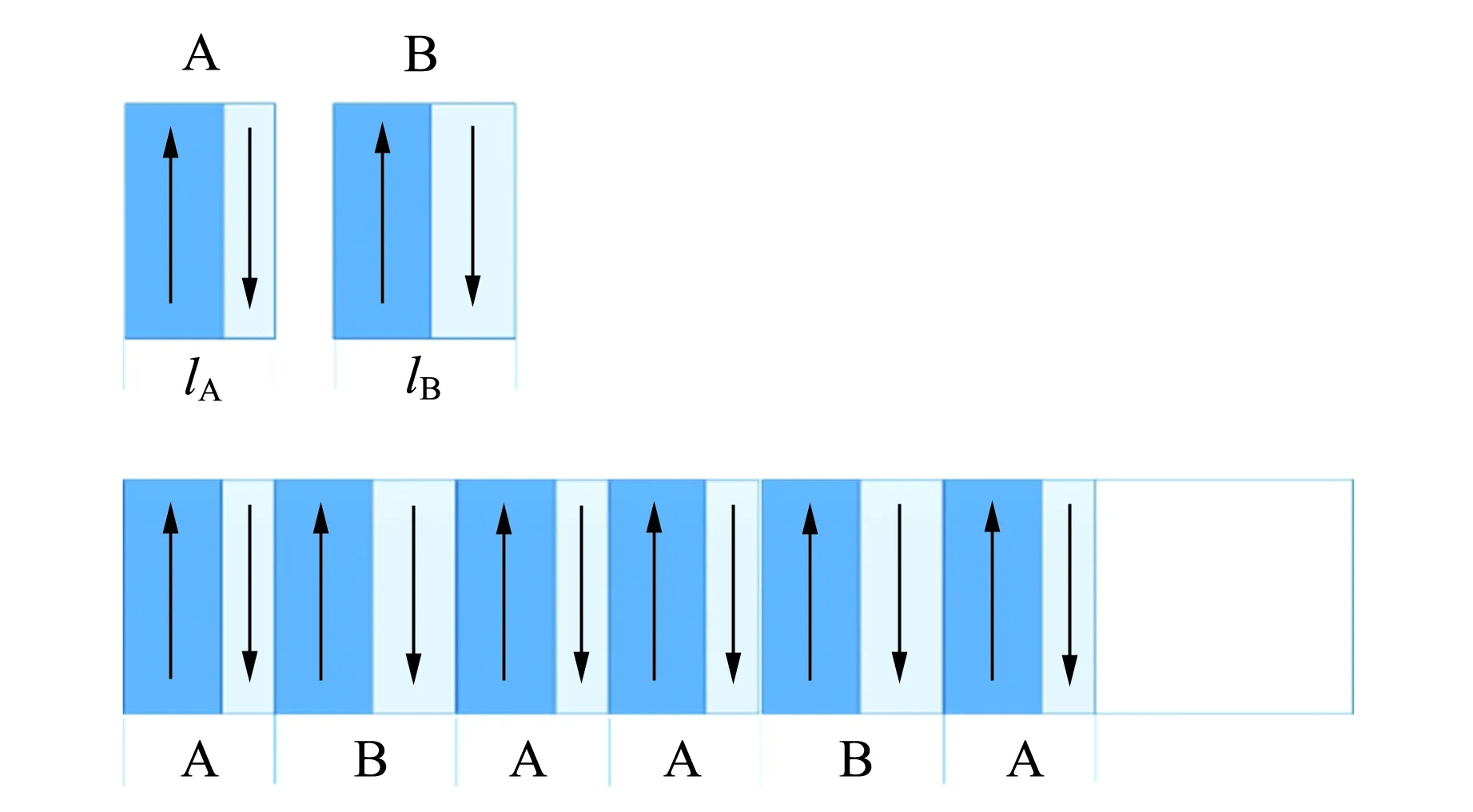
图3 准周期光学超晶格结构示意图
设迭代操作的矩阵为T,并遵循下面的变换规则:TA=AB,TB=A. 令Sn=TnA,则有:
S0=A,
S1=AB,
S2=ABA,
Sn+1=SnSn-1.
这样构造出来的结构是一维的Fibonacci序列,其提供的倒格矢可以写为
基于多重准相位匹配原理的准周期光学超晶格的重要应用是实现高效的激光三倍频,获得短波长激光光源. 要实现三倍频,通常的做法是使用2块非线性晶体. 第1块晶体中完成基频光的倍频过程ω+ω→2ω,第2块晶体中完成基频光和倍频光的和频过程从而获得三倍频ω+2ω→3ω. 这2个非线性光学过程是分开进行的. 如果使用准周期光学超晶格作为非线性频率转换晶体,其可以提供2组独立的倒格矢,从而可以在1个结构中同时完成这2个非线性过程,而且这2个过程是同时发生的,称为耦合的光参量过程. 利用准周期Fibonacci序列的光学超晶格,南京大学的课题组在1997年成功制备出准周期钽酸锂光学超晶格,使用其提供的2个倒格矢G1.1和G2.3,分别补偿了倍频及和频过程的波矢失配,实现了耦合的直接三倍频过程[11],如图4所示.
准周期光学超晶格中的耦合三倍频实验的基波光源是1台脉冲宽度8 ns,重复频率10 Hz的
光参量振荡器,工作波长选取为1.570 μm. 在8 mm长的准周期钽酸锂光学超晶格中,获得了直接的三倍频绿光输出,见图5. 当输入基波光的功率为26 mW时,输出三倍频功率为6 mW,从1.570 μm近红外光到0.523 μm绿光的三倍频转换效率高达23%.
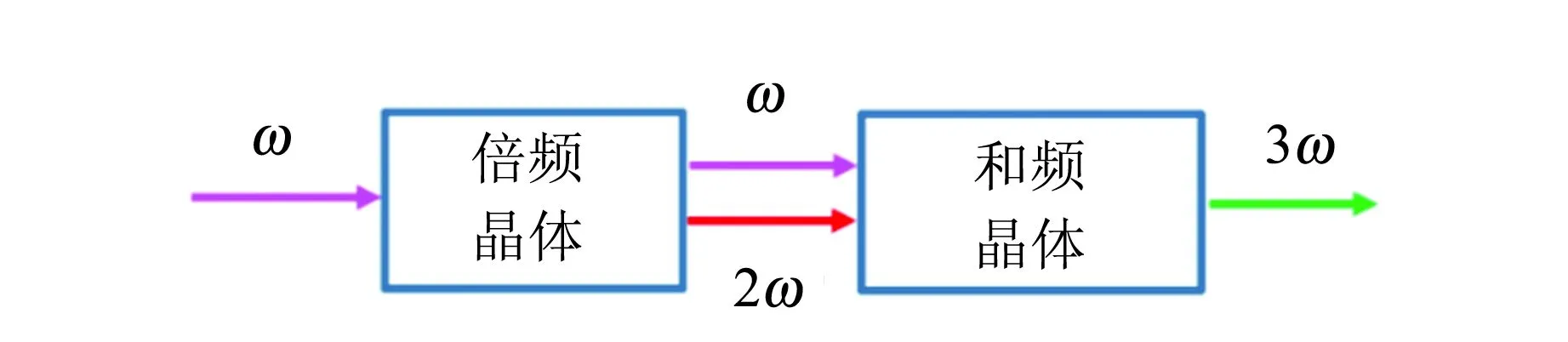
(a)2块非线性晶体产生三倍频
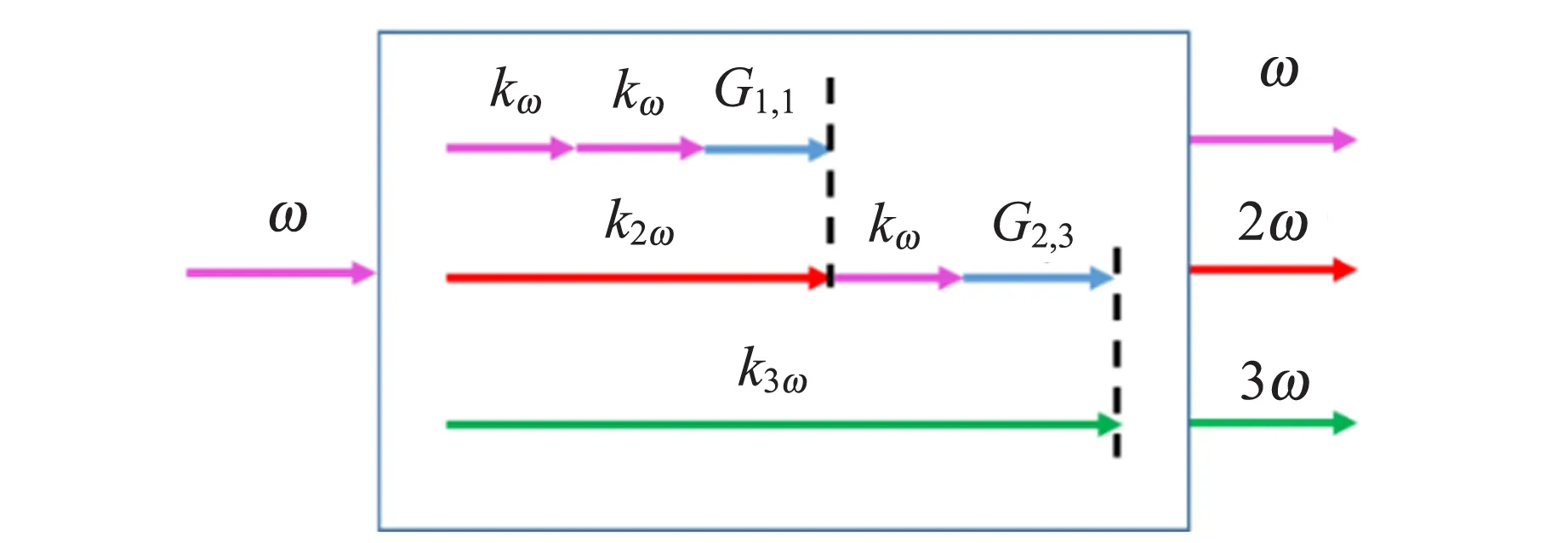
(b)准周期超晶格中耦合三倍频图4非线性晶体中产生三倍频的两种方案

图5 准周期光学超晶格中直接三倍频产生的绿光
3 红绿蓝三基色激光器
在此基础上,南京大学的研究组进一步发展了基于多重准相位匹配原理的多波长激光器,其中最具有代表性的是光学超晶格红绿蓝三基色激光器[12-14]. 产生红绿蓝三色激光光源,通常的方案是使用3台近红外波段的激光器,工作波长一般在1.3 μm,1.06 μm和0.9 μm附近,通过3块倍频晶体分别产生红光、绿光和蓝光[15-16]. 能否使用1台激光器和1块非线性晶体来实现更加紧凑高效的三色激光光源,一直是人们努力的目标. 南京大学的研究组提出了基于激光二极管泵浦双波长激光器和多重准相位匹配光学超晶格的方案. 该方案使用的激光光源是激光二极管泵浦的Nd∶YAG双波长激光器,激光器的工作波长对应于Nd3+的2条较强的发射谱线1 319 nm和1 064 nm,见图6. 1 319 nm谱线倍频可以获得660 nm的红光;1 319 nm近红外光和660 nm红光和频可以产生440 nm的蓝光;1 064 nm近红外光倍频则可以获得532 nm的绿光. 非线性晶体是1块准周期结构级联周期结构的钽酸锂光学超晶格. 准周期结构提供的G1,1倒格矢用于补偿1 319 nm倍频的波矢失配产生660 nm红光;G3,4倒格矢用于补偿和频过程的波矢失配产生440 nm蓝光;第二段周期结构的一阶倒格矢用来补偿1 064 nm倍频过程的波矢失配,产生532 nm绿光.
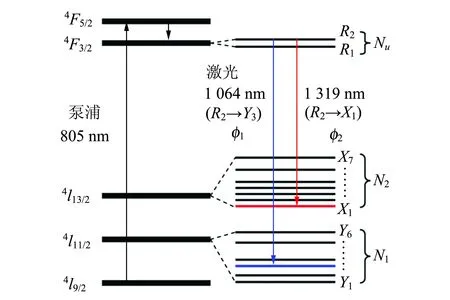
图6 Nd∶YAG激光增益晶体的能级图
对于Nd∶YAG激光器,因为1 319 nm和1 064 nm 2条发射谱线拥有共同的上能级,因此处于双波长工作状态时,2条输出谱线会存在竞争,导致输出功率不稳定. 在红绿蓝三基色激光器的基波光源方面,使用了间歇振荡双波长激光技术[17]. 如图7所示,设计Y型的谐振腔,2支谐振腔共享1块激光增益晶体Nd∶YAG,在每支腔内分别放置了1 319 nm和1 064 nm的声光调Q开关,这2个声光Q开关的开关时间通过电路来设置延迟,让它们在不同的时间段开启,见图8. 通过间歇振荡的双波长激光技术,一方面克服了2支谱线输出功率竞争的问题,另一方面通过调节2个声光Q开关的延迟时间,还可以调节2支波长的输出功率比值.
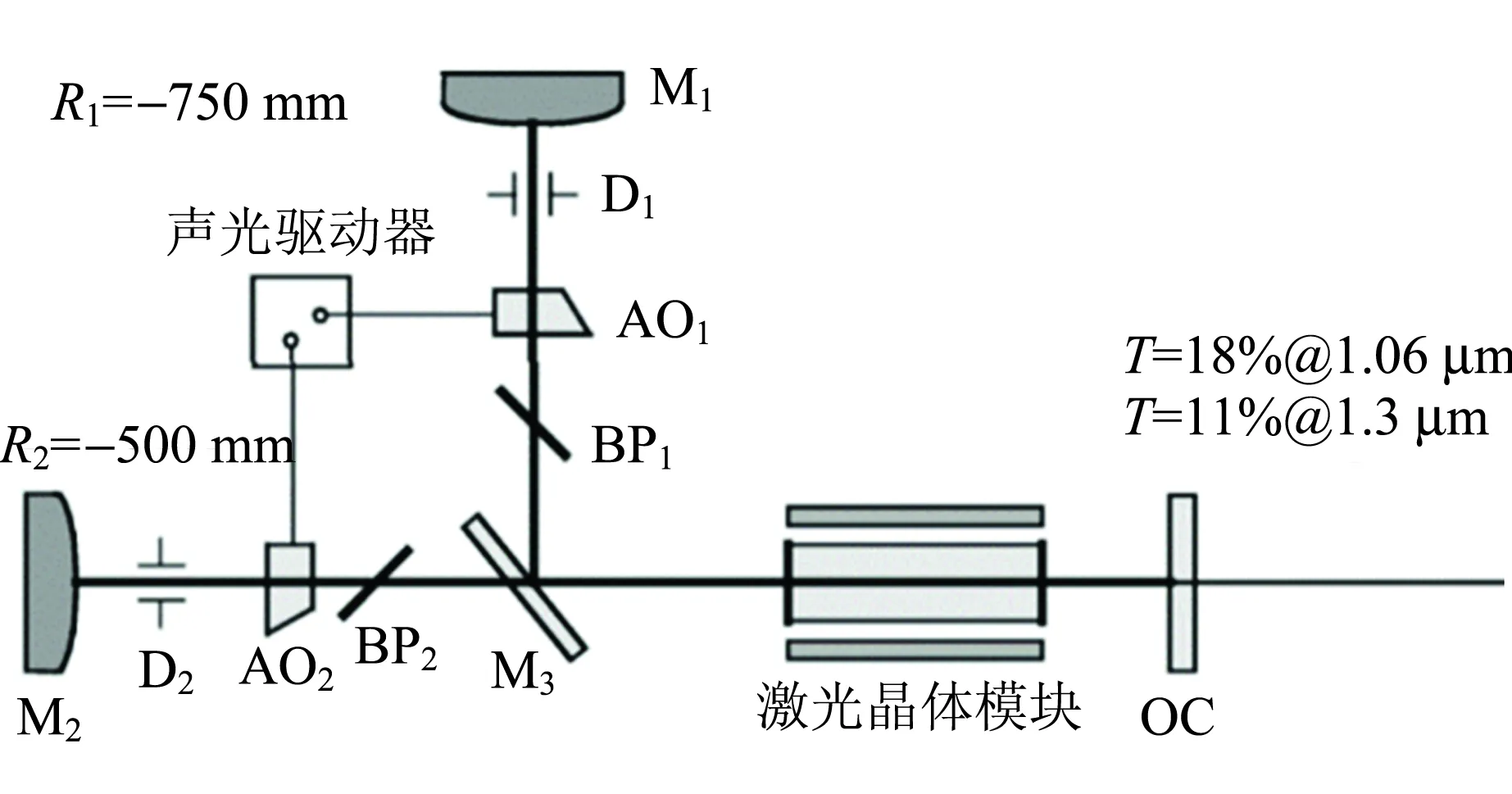
图7 间歇振荡双波长激光器示意图
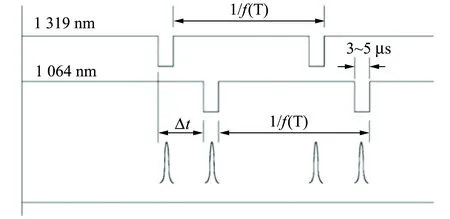
图8 2个声光Q开关的时延关系图
使用1 319 nm和1 064 nm间歇振荡双波长激光器作为基波光源,级联结构的光学超晶格作为非线性晶体,可以实现使用1台激光器和1块非线性晶体,红绿蓝三色激光的同时输出(图9). 因为晶体材料的色散与温度相关,因此调节超晶格晶体的温度,可以改变3种颜色激光的输出功率比例,如图10所示. 当调节2个声光Q开关的开关延迟时间使得入射的1 319 nm和1 064 nm的基波光功率分别为3.9 W和1.2 W,调节晶体的温度为129.3 ℃时,可以获得780 mW的红光、146 mW的绿光和84 mW的蓝光输出,功率比例为9.3∶1.7∶1. 3种颜色的光混合在一起,接近色度图上的冷白光点,色温为5 000 K. 准白光的输出总功率为1.01 W,从基波光到准白光的转换效率约为20%.

图9 光学超晶格三基色/准白光激光器输出激光

图10 红绿蓝三色激光的输出功率随着晶体温度的变化关系
4 非线性Talbot效应
光学超晶格除了应用于激光频率转换构建新型的光源外,还可以演示诸多光与物质相互作用的新颖光学效应. 例如在二维光学超晶格中实现准相位匹配增强的弹性散射[18],利用这种新效应可以测得弹性散射在铁电晶体中的分布,为晶体质量和微结构的表征提供了一种有效的方法;演示了粒子物理中切伦科夫辐射的光学类比非线性切伦科夫辐射效应[19-22]、非线性布拉格衍射[23]、非线性拉曼内斯衍射[24]和空间光束的非线性产生[25-27]等. 近来,南京大学的课题组还实现了基于铌酸锂的首个量子光学芯片[28-29],将纠缠光子源、电光调制器、光子干涉仪等功能单元成功集成在1块基于光学超晶格的铌酸锂光子芯片上,实现了纠缠光子产生和调控的一体化设计,完成了纠缠光子对聚束态和分离态的快速切换. 这一工作是全固态量子芯片研究方面的重要进展, 对铌酸锂量子逻辑门和量子模拟芯片研究有力推动.
下面介绍传统线性Talbot效应在非线性光学领域的拓展,即光学超晶格中的非线性Talbot效应.
1836年,Henry Fox Talbot用1束白光源照射光栅,在光栅后面的一定距离处观察到了光栅自身的像. 人们把这种现象定义为Talbot效应,又叫做无透镜成像[30]. Talbot本质是空间相干平面波的干涉衍射效应. 在傅里叶光学中,周期性的物体可以表示为
式中,d是空间周期,cn是n阶谐波的振幅. 根据菲涅尔-基尔霍夫衍射理论,衍射光场的振幅E(X)为
其中,S(xs)是光源的振幅,X,x和xs分别是笛卡尔坐标系下的观察平面、物平面和光源平面的坐标,z1是光源和物之间的距离,z2是物和观察平面之间的距离.
当使用平面单色光照射一维线性光栅时,衍射光场的振幅可以表示为
在某个特定的传播距离上,所有的衍射级次同相从而相长干涉:
zT=2d2/λ.
其中,d是光栅周期,λ为入射光的波长,zT所谓的Talbot距离. Talbot距离与周期性物体的周期的平方成正比,与波长成反比. 图11给出的是一维Talbot自成像的光强分布图.
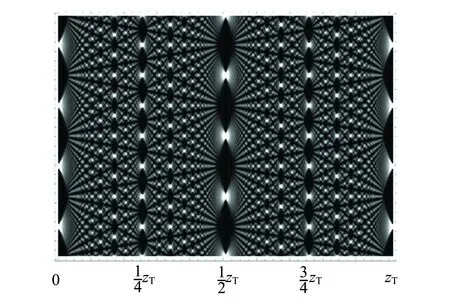
图11 一维光栅在单色平面光照射下的Talbot自成像光强分布图
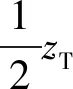
非线性Talbot效应是对传统Talbot效应在概念上的拓展. 在非线性Talbot效应中,利用周期极化光学超晶格中产生二次谐波产生的自成像效应[31-36]. 在光学超晶格晶体中二阶非线性光学系数χ(2)的符号是周期性分布的,即正畴是+χ(2),负畴是-χ(2),但是正畴和负畴的折射率相同,也就是说整超晶格样品的折射率分布是均匀的. 线性光栅反映的是折射率自成像,而二次谐波Talbot效应反映的是二阶非线性系数χ(2)的自成像.
研究非线性Talbot效应的实验光路示意图如图12所示.
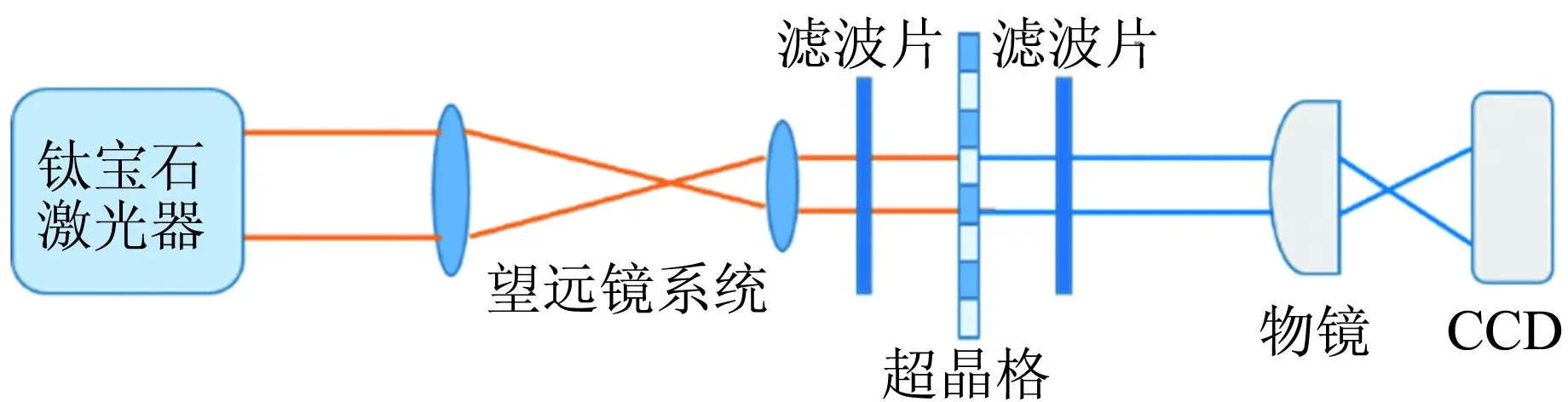
图12 研究非线性Talbot效应的实验光路示意图
光源是1台脉冲宽度75 fs、重复频率80 MHz的钛宝石飞秒激光器,工作波长为800 nm. 激光器出射的光束经望远镜系统整形后,照射至光学超晶格样品上. 在该实验体系中,可以近似认为入射到样品表面的光波是平面光. 在样品的前后两侧各放置滤光片,以避免杂散光对实验的干扰. 放大倍率100、数值孔径0.7的物镜置于高精度的三维调节架上,放在第2个滤光片后. 沿着光路的光轴方向,改变物镜距超晶格样品的距离可以观察到倍频光在不同位置上的成像情况. 物镜后面放置CCD用以接收和记录实验结果.
首先,在实验中研究了一维非线性 Talbot效应,所使用的的样品是一维周期极化的钽酸锂光学超晶格,周期为8.0 μm,占空比约为50%,样品的SEM图如图13所示. 当入射基波光为平面光时,一维周期极化光学超晶格的Talbot距离是zT=4Λ2/λp,其中Λ是超晶格样品的极化周期,λp是基波光的波长. 和线性的情况相比较,非线性Talbot距离中的系数“4”是线性情形的2倍,究其原因,是因为非线性Talbot效应是由非线性过程产生的倍频光产生的,而不是由入射的基波光产生的. 基波光的波长是倍频光的2倍,所以造成了系数的2倍关系. 图14分别给出了第1个和第3个Talbot平面上的倍频光干涉图像. 在第1个Talbot平面上,可以明显地看到周期性的谐波干涉条纹,其中亮条纹对应的是铁电畴区域,而暗条纹对应的是正负畴的畴界. 第3个Talbot平面的成像质量明显要比第1个Talbot距离的差,其原因在于,二次谐波的高阶信息随着传播距离加长,损失得越来越多,带来自成像的效果变差. 在光学超晶格的制备工艺中,总会存在制作误差,图13中红色部分标注的是线条窄一点的铁电畴,在后续的自成像中这根窄线条的铁电畴没显示出来. 这是因为在Talbot效应中,只有周期性的结构才能自成像,局部的小缺陷不能自成像,因此没有在整数阶的Talbot平面上被观察到.

图13 一维周期极化光学超晶格畴结构的SEM图

(a)第1个Talbot平面上

(b)第3个Talbot平面上图14 Talbot平面上的信频自成像图案
通过上述的实验现象,可以进一步加深对非线性Talbot效应物理图像的认识:非线性Talbot成像不同于传统的线性Talbot自成像,是非线性过程产生的倍频光的干涉衍射在光学超晶格晶体的出射面上产生的周期性的光强图像. 非线性Talbot效应实际上可以等效为2个级联的光学过程:第一个过程是发生在周期极化光学超晶格中的倍频过程. 因为晶体中周期性畴结构的存在,所以在超晶格晶体的后表面出现了相同周期的倍频光的光强分布,这种周期性的光强图作为非线性自成像中的周期性物体. 第二个过程是产生的倍频光在自由空间的传播过程,周期性的倍频光在自由空间的干涉衍射形成倍频的Talbot效应,这与线性的Talbot效应类似.
5 结束语
从1962年Bloembergen提出准相位匹配原理,已经经过了1个甲子. 相关领域包括了材料的制备和表征、基础理论的发展、激光技术方面的应用以及其中光与物质相互作用所展示的各种新颖光学效应. 限于篇幅,本文仅仅介绍了南京大学的研究组在发展基本理论、研制新型激光器以及发现新颖光学效应等方面的工作,在微结构的设计方面,在传统周期结构的基础上引入准周期的结构,将准相位匹配理论推广到多重准相位匹配理论,研制了高效、集成化的多波长激光器. 最近,研究组进一步发展了局域准相位匹配理论,在频率转换的同时调控谐波的波前相位,实现聚焦、分束,特殊光束产生等多功能集成. 在超晶格中,也发现了很多新颖的光学效应,例如本文中提到的非线性Talbot效应. 目前已经在南京大学物理实验中心转换为本科生物理实验项目的非线性切伦科夫辐射,是在实验室用光学的方法模拟粒子物理的相关实验[37-38]. 光学超晶格中其他新颖的光学效应,诸如非线性布拉格衍射和非线性拉曼内斯衍射等,也可以从教科书中找到线性的对照. 希望光学超晶格相关研究中蕴含的思维方式能够对大学物理实验教学的开展有所启示.

