Closed-Form Solutions to the Crack and/or Rigid Line Inclusion in 1D Orthorhombic Quasicrystals

WANG Wenshuai(汪文帅),YUAN Hongting(袁宏婷)

( School of Mathematics and Statistics,Ningxia University,Yinchuan 750021,China)

Abstract: The problem of the one-dimensional(1D) orthorhombic quasicrystals with a crack and/or rigid line inclusion of antiplane mode is investigated through introducing the generalized complex variable method.For 1D orthorhombic quasicrystals,considering of the periodic (x 1,x 2)-plane of atomic structures with the quasiperiodic directionx 3-axis along which there exists a phason displacement,and the macroscopical crack and/or rigid line inclusion,which is placed on the periodic (x 1,x 2)-plane,we focus on finding out the influence of phason displacement on the related physical quantities.By the generalized complex variable method,these two models are reduced to the Riemann–Hilbert problems,and the closed-form solutions of the phonon and phason fields for antiplane mode are obtained.The explicit solutions of stress intensity factors for phonon field and phason field are obtained respectively,which are very useful in the fields of fracture mechanics and engineering.The results show that the phonon and phason stress intensity factors of crack as well as the factors of rigid line inclusion are not related to the coupling of phonon and phason fields.These imply that,for antiplane mode,there is no influence of phason displacement on both the phonon stress intensity factor (usual stress intensity factor) of crack and the phonon stress field intensity factor of rigid line inclusion.The obtained analytical solutions will provide necessary reference for material design and numerical solutions.

Key words: Orthorhombic quasicrystal;Crack;Rigid line inclusion;Generalized complex function; Stress intensity factor

1.Introduction

Shechtman was awarded the Nobel Prize of Chemistry 2011 due to the discovery of quasicrystals in 1982,which has aroused great interest in the fields of structure and material again[1].As we all know,the field of linear elasticity theory of quasicrystals has been investigated for many years[2−3]and the mathematical elasticity theory of quasicrystals has been developed by FAN and his coworkers[4−5].As a material,quasicrystal is deformable under external loads,thermal loads and certain internal effects,which makes it very sensitive to defects such as cracks.So,finding solutions of dislocations and cracks in quasicrystals is the core of the static and dynamic elasticity theory[6],and the study of defect problem of quasicrystalline materials is meaningful both in theoretical and practical applications.We noticed that there were many high-precision numerical methods in solving defect problems in quasicrystals[7−9].In this paper,we do not investigate the numerical methods but limit ourselves to analytical solutions.As for analytical solutions,some investigators developed various methods to obtain the analytical solutions for defect problems of quasicrystals[6,10],such as Fourier transform method[11],perturbation method[12],complex variable method[13],boundary integral equation method[7],and the method of Green’s functions[14].

Recently,generalized Hooke’s law of quasicrystals has been derived systematically,which provides a fundamental theory based on the notion of a continuum model to describe the elastic behavior of quasicrystals[4].Therefore,some methods like complex variable method,based on the generalized Hooke’s law,get a new development opportunity.It is well known that the complex variable method,initially developed by Muskhelishvili,is an effective method for solving various elasticity and defect problems[15].It is also developed to solve defect problems of quasicrystals.For 1D hexagonal quasicrystals,many efforts have been made in the fields of the mechanic involving elasticity and defects by the complex variable method[16−18].For instance,the collinear periodic cracks and/or rigid line inclusion of antiplane mode in 1D hexagonal quasicrystals have been studied[19].Considering that the surfaces of the cracks and holes are in limited permeable boundary conditions,the antiplane problem of an elliptical hole with two asymmetrical cracks in 1D hexagonal quasicrystals with piezoelectric effect is investigated by adopting the technique of conformal mapping and the Stroh-type formulism[13].

As the structure of 1D orthorhombic quasicrystals is more complex than that of 1D hexagonal quasicrystals,it leads to the elasticity and defect problems in 1D orthorhombic quasicrystals having greater difficulties to solve directly with classical elastic method.Note that the elasticity and defect problems for 1D hexagonal quasicrystals have been extensively researched[16−18],but only a few results are on the issue of 1D orthorhombic quasicrystals with defects.By introducing generalized conformal transformation and using complex variable function method,the problem about 1D orthorhombic quasicrystals with an elliptical hole is investigated[20].Under limited conditions,the problem of an elliptical hole degenerates into the problem of a Griffith crack,and the implicit analytical solutions in stress field and the stress field intensity factors are obtained corresponding to the crack problem.By employing a new displacement potential function and using a half-inverse method,YU et al.[21]developed the results obtained in literature[20]through eliminating the dependence on the characteristic root.As an application,the closed-form solutions are obtained for wedge problems or halfplane problems of 1D orthorhombic piezoelectric quasicrystals by introducing four potential functions[2].LI et al.[3]investigated the problem of a functionally graded multilayered 1D orthorhombic quasicrystals plate with simply supported edge conditions.GAO et al.[22]gave the analytical solutions for problems of 1D orthorhombic quasicrystal with semi-infinite crack.In this work,we focus on the analytical solutions of crack and/or rigid line inclusion problems for 1D orthorhombic quasicrystals by generalized complex variable method.Assuming the(x1,x2)-plane of atomic structures is periodical,and the quasiperiodic direction isx3-axis along which there exists a phason displacement,and the macroscopical crack or rigid line inclusion is placed on the periodic (x1,x2)-plane,we work on finding out the influence of phason displacement on the related physical quantities.These two models are reduced to the Riemann-Hilbert problem of generalized complex functions to obtain the closed-form solutions for antiplane mode[23].And exact solutions are obtained by means of generalized complex variable method.The stress intensity factors for phonon field and phason field are obtained respectively,which are very useful in practice.

2.Basic Mathematical Description

For 1D orthorhombic quasicrystals,there is a periodic(x1,x2)-plane of atomic structures with the quasiperiodic directionx3-axis along which there exists a phason displacement.There is a crack or rigid line inclusion in the periodic (x1,x2)-plane,and its location is specified by interval[−a,a]onx1-axis.The infinite plane of 1D orthorhombic quasicrystals is subjected to external antiplane stresses of the phonon and phason fields asat infinity(see Fig.1).The fracture analysis of the problem can be expressed through the superposition of two problem solutions.The first solution refers to the elastic problem of infinite plane for 1D orthorhombic quasicrystals under an external antiplane stresses of the phonon and phason fields asat infinity,without crack or rigid line inclusion.The second problem describes the stress distribution of the crack or rigid line inclusion in an infinite plane for 1D orthorhombic quasicrystals,and the external loads are limited to the crack or rigid line inclusion surface traction.These external loads are equal in magnitude and opposite in sign to the obtained stresses in the imaginary crack line or rigid line inclusion as described by the first problem.It is obvious that the solutions to the second problem contain singularities.

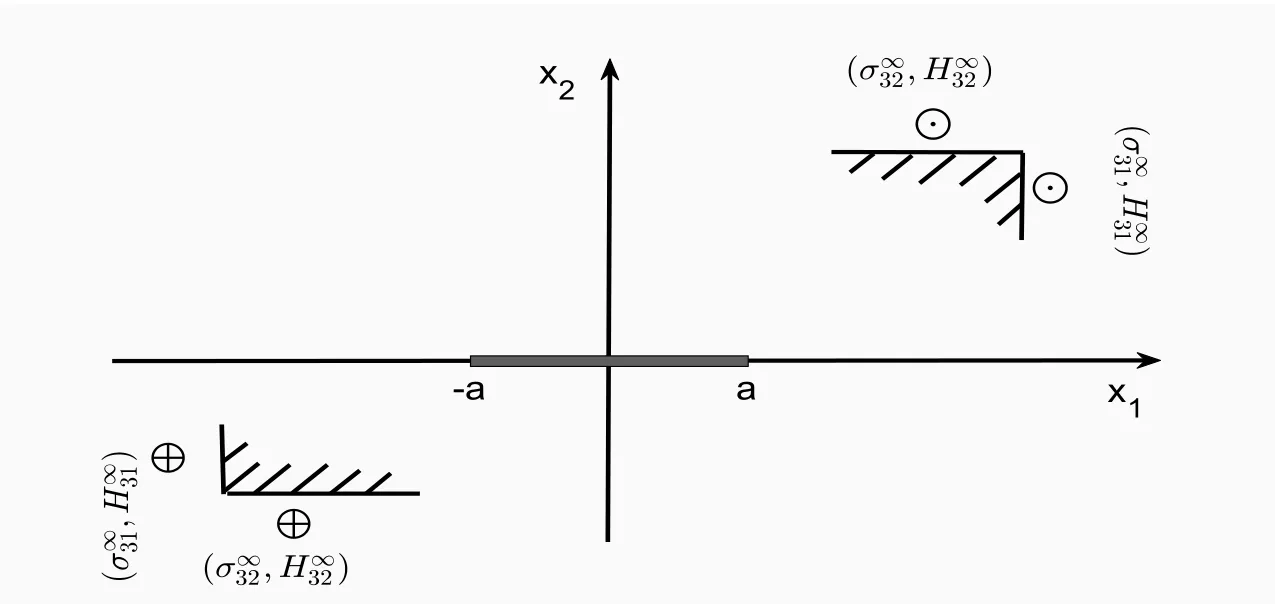
Fig.1 The crack and/or rigid line inclusion on physical plane

With the help of phonon and phason strains

wherei,jare the repeated indices denoting summation,εij,uiare the strain and displacement of the phonon field,respectively,wijare the strain of the phason field,and a comma in the subscripts stands for partial differentiation.Then the constitutive equations of 1D orthorhombic quasicrystals can be written as follows[24]

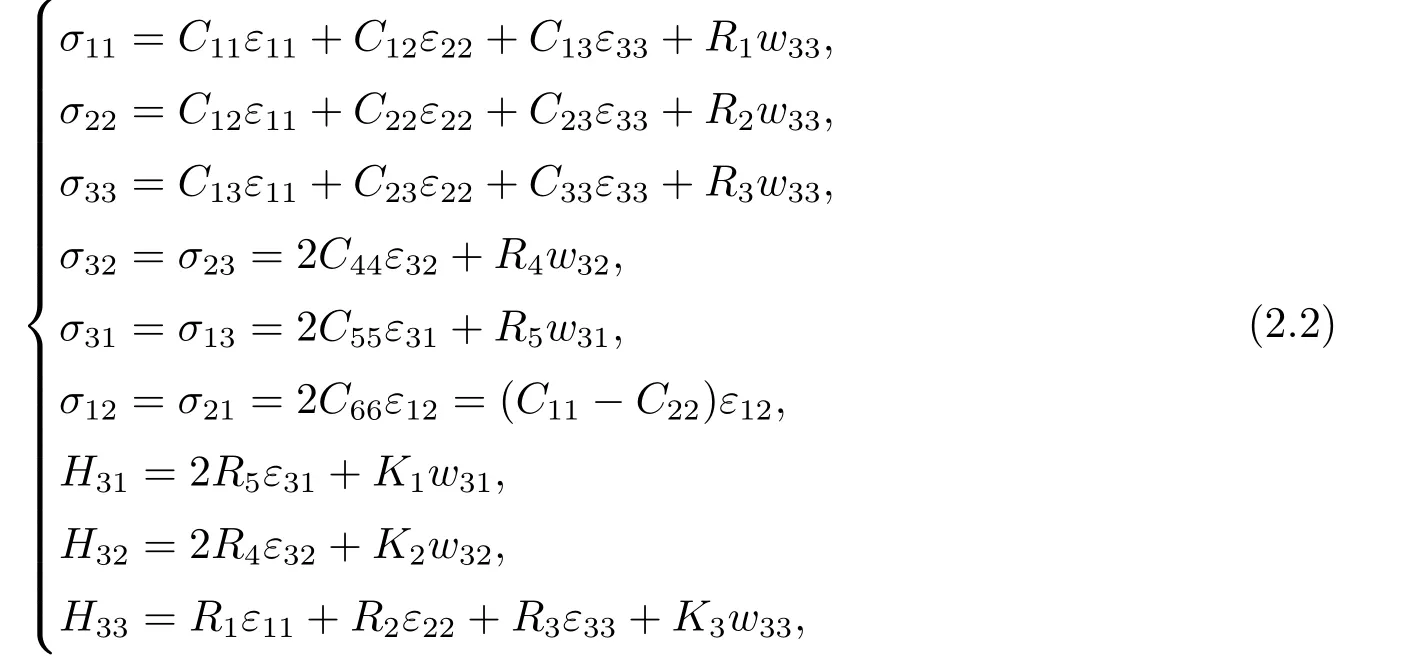
whereσijare the phonon stresses,which are the same as those in usual crystals,Hijare new and named as the phason stresses with which the movement of atoms through barriers can come true when the quasilattices rearrange,CijandKiare the elastic constants of phonon field and phason field,respectively,andRiare phonon-phason coupling constants.Under antiplane mode,assuming thatu1=u2=0,u3=u3(x1,x2),w3=w3(x1,x2) in the constitutive equation (2.2),we have

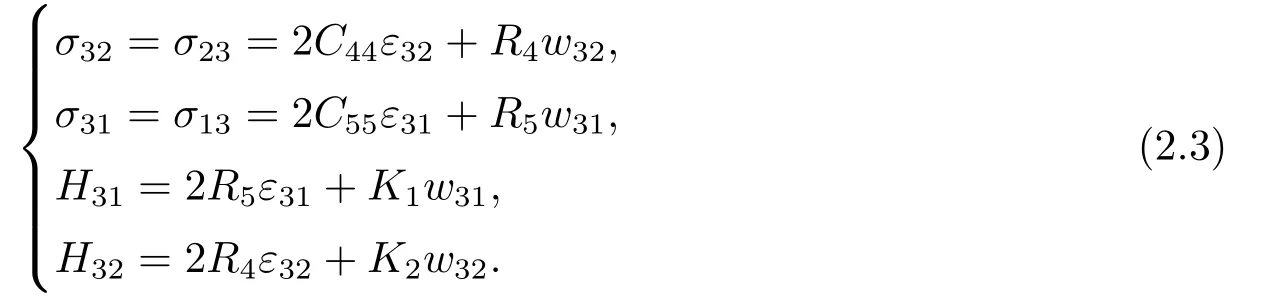
Under the static condition,the phonon and phason stresses should satisfy the following generalized equilibrium equation

Substituting Eqs.(2.1) and (2.3) into Eq.(2.4) yields the coupled governing equation of 1D orthorhombic quasicrystals

A potential functionU(x1,x2),which is introduced to solve the coupled governing equation (2.5),has a correlation with the phonon strainsu3and the phason strainsw3

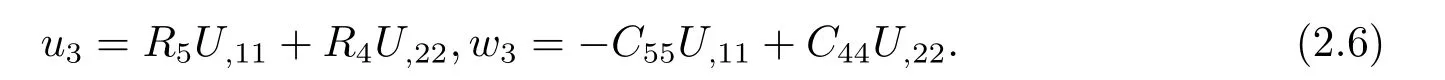
It is readily found that the first formula of Eq.(2.5) is fulfilled from Eq.(2.6).Then,substituting Eq.(2.6)into the second formula of Eq.(2.5),one can obtain the following relation

where

The characteristic equation of Eq.(2.7) is

and the characteristic roots of Eq.(2.7) are

The multiple harmonic functionU(x1,x2) may be represented as the real part of generalized complex functionsU1(z1) ofz1=x1+µ1x2andU2(z2) ofz2=x1+µ2x2,

Then,the phonon displacement and stresses as well as the phason displacement and stresses can be expressed by these generalized complex functionsU1(z1) andU2(z2) readily

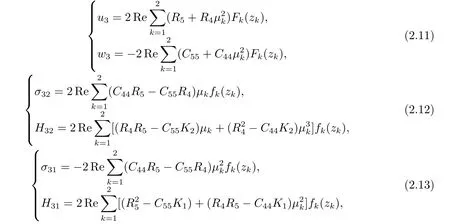
3.The Problem of Crack

Here,the fundamental solution of crack is considered when a pair of equivalent antiplane shear traction of the phonon and phason fields,σ0(x1) andH0(x1),act on the crack surface.Then,the corresponding boundary conditions on the crack surface are imposed

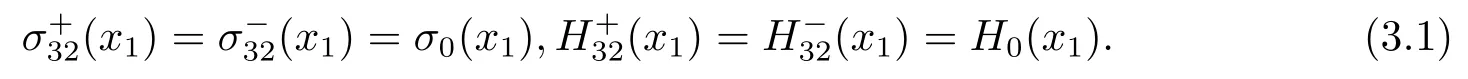
On the junction surface,the stress-continuity conditions are satisfied

So,the stresses are continuous alongx1.Considering Eq.(2.12),one can obtain the following relations

Based on that

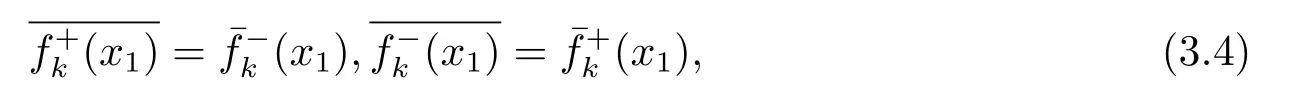
Eq.(3.3) is changed into

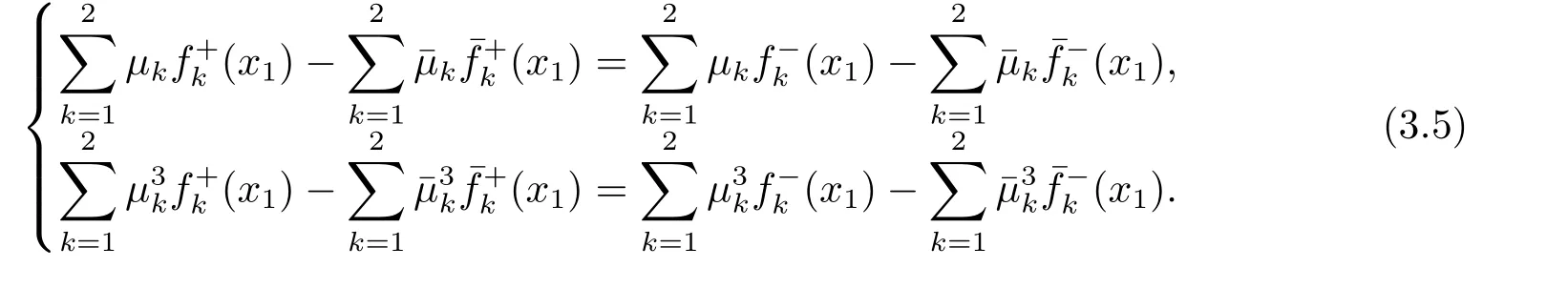
Noting that the left formulas of the above equation are the boundary value of the generalized complex functions whenx2>0,and the right formulas are that whenx2<0,hence,the generalized complex functions are analytic in the whole plane.Furthermore,the complex functions are constants.There is no stress hypothesis at infinity,so the constants are zeros.For this reason,we can achieve the following relations

Considering Eqs.(3.4) (3.6) and (2.12),we have

From Eq.(3.1),we get

Here Eq.(3.8) is changed into new forms for easy calculation

From Eq.(3.9),we obtain

where

Eq.(3.10)is a group of Riemann-Hilbert problems for two generalized complex functions.Referring to the theory of Riemann-Hilbert problems,we obtain the general solutions

where

A special case considered here is that the infinite plane of 1D orthorhombic quasicrystals is subjected to antiplane stresses of the phonon and phason fields asat infinity.Then,the equivalent loading on the crack surface for this special case is

Some marks are introduced as

Then,in this special case,we have

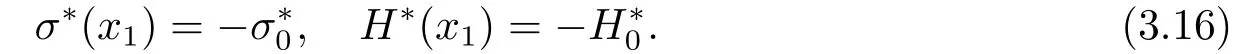
Furthermore,we get

Considering that

we have

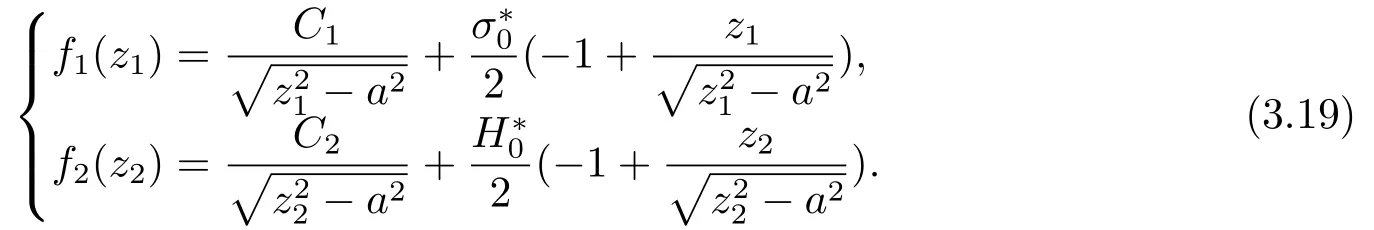
Single value condition of generalized displacement demands that the displacement should be returned to the initial value after going around the crack for one circle.So,we have

Hence,Eq.(3.19) is simplified as

Then,the phonon stresses as well as the phason stresses can be expressed as

Using Eq.(3.15),one can find that

Further,the stress formulas (3.22) are deduced by using Eq.(3.23)

Obviously,for the crack surface,are the pure imaginary,

whereβ(x1) is a real number function forzk=x1∈(−a,a).

So,the stress formulas along the crack surface can be expressed as follows

Further,the stress formulas along the crack surface are deduced through Eq.(3.23)

It is readily found that the stress formulas Eq.(3.14)are fulfilled along the crack surface.

Furthermore,the gradual fields around the right crack-tip are analyzed.The discussion is limited in the local coordinate system(r,θ)aroundx1=a.Whenzk→a+,one can obtain thatzk−a=r(cosθ+µksinθ),zk+a=2a,so the gradual form (3.10) can be expressed as follows

Moreover,the vector stress intensity factor[20]of the crack can be defined as

whereKσandKHdenote the stress intensity factors of phonon field and phason field,respectively.

From Eq.(3.28),one can compute the stress intensity factors as follows

One can get the stress intensity factors as follows from Eqs.(3.23) and (3.30)

4.The Problem of Rigid Line Inclusion

Here,the fundamental solution of rigid line inclusion is considered when a pair of equivalent antiplane shear traction of the phonon and phason fields,σ0(x1) andH0(x1),act on the surface of rigid line inclusion.Then,the corresponding boundary conditions on the surface of rigid line inclusion are imposed

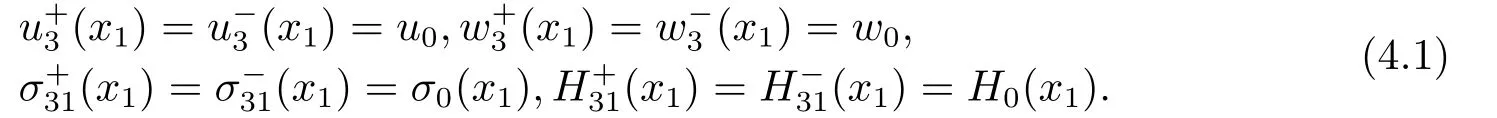
The displacement-continuity conditions are satisfied

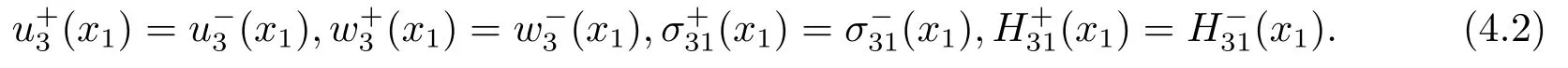
From Eq.(4.1),we have

So,Eq.(4.3) are fulfilled alongx1.

Based on that

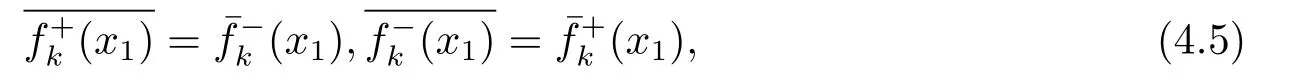
the above equation is changed into

As the left formulas of the above equation are the boundary value of the generalized complex functions whenx2>0,and the right formulas are that whenx2<0,the generalized complex functions are analytic in the whole plane,furthermore,the complex functions are the constants.There is no displacement hypothesis at infinity,so all the constants are zero.For this reason,we can achieve the following equations

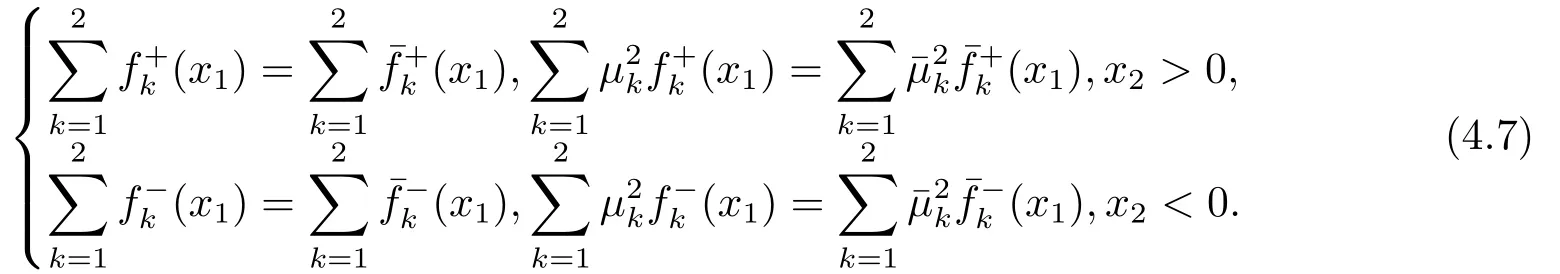
Considering Eqs.(2.13),(4.5) and (4.7),we have

From Eq.(4.1),we have

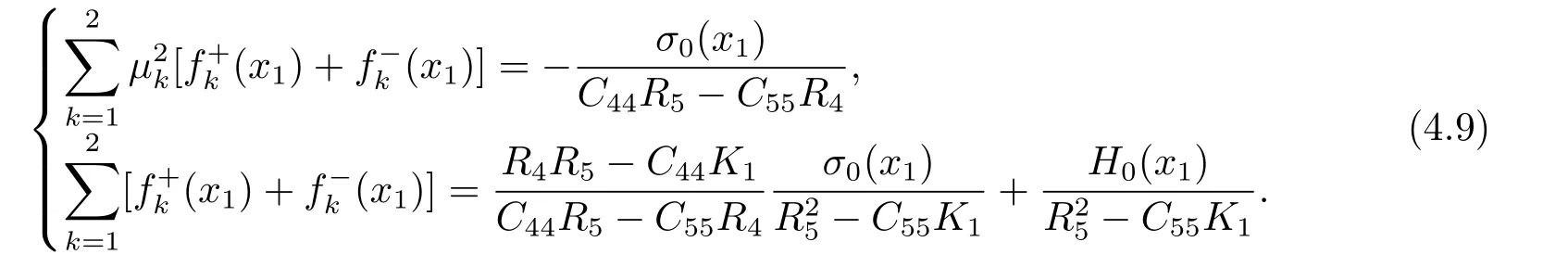
Eq.(4.9) can be changed into new forms for easy calculation

From Eq.(4.10),we obtain

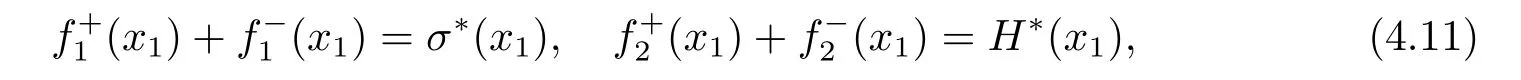
where

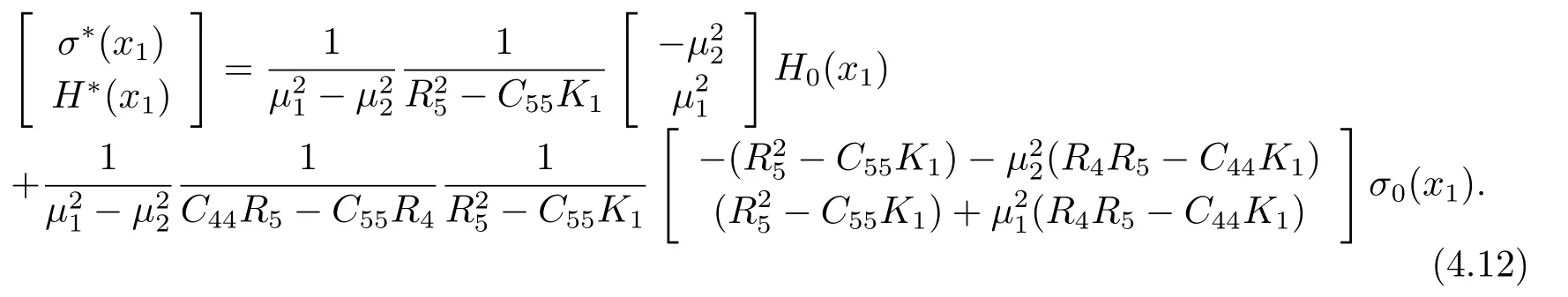
Eq.(4.11)is a group of Riemann-Hilbert problems for two generalized complex functions.Referring to the theory of Riemann-Hilbert problems,we obtain the general solutions

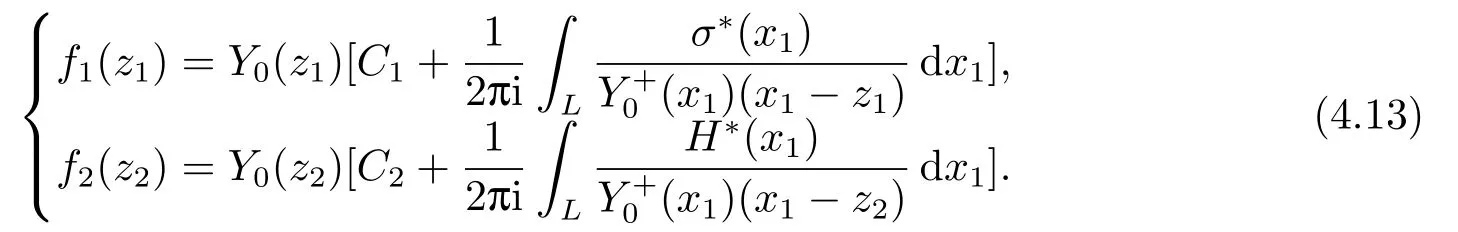
A special case considered here is that the infinite plane of 1D orthorhombic quasicrystals is subjected to antiplane stresses of the phonon and phason fields asat infinity.Then,the equivalent loading on the inclusion surface for this special case is

Some marks are introduced as

Then,in this special case,we have

And,we obtain

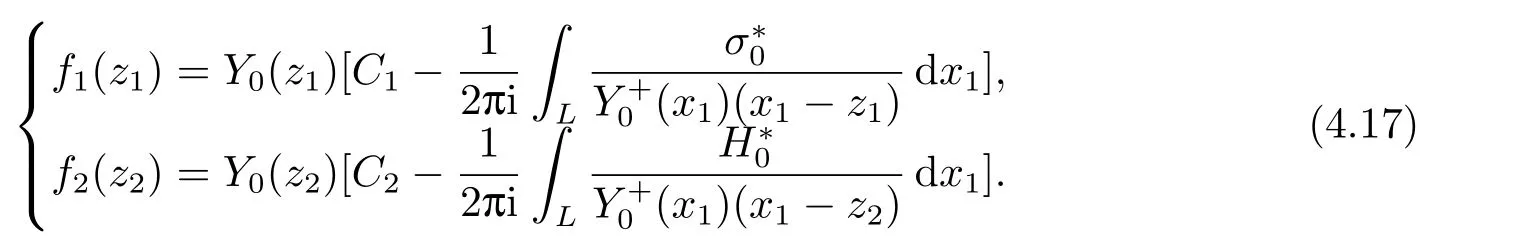
Considering Eq.(3.18),we get

Single value condition of generalized displacement demands that the displacement should be returned to the initial value after going around the crack for one circle.So,we haveC1=C2=0.Then,Eq.(4.18) is simplified as

Then,the phonon stresses as well as the phason stresses can be expressed

Using Eq.(4.15),one can find that

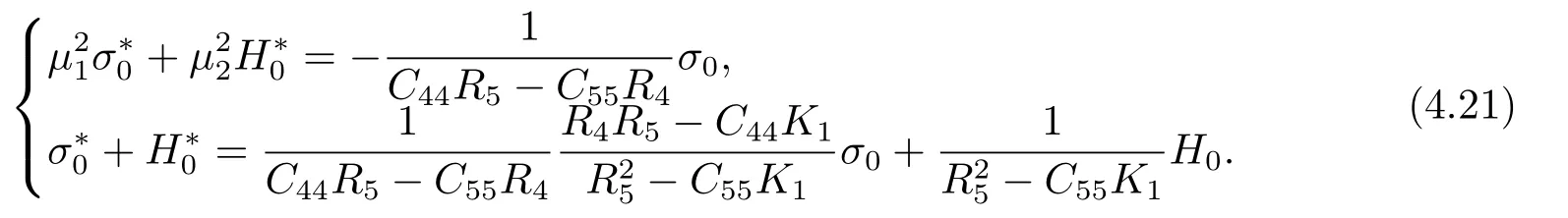
Further,the stress formulas (4.20) are deduced by using Eq.(4.21)

Obviously,for the inclusion surface,are the pure imaginary,

whereβ(x1) is a real number function forzk=x1∈(−a,a).

So,the stress formulas along the crack surface can be expressed as follows

Further,the stress formulas along the crack surface are deduced by using Eq.(4.21)

It is readily found that the stress formulas (4.1) along the inclusion surface are fulfilled.

Furthermore,gradual fields around the right tip of the inclusion are analyzed.The discussion is limited to the local coordinate system (r,θ) aroundx1=a.Whenzk→a+,one can obtain thatzk−a=r(cosθ+µksinθ),zk+a=2a,so the gradual form (4.22) can be expressed as follows

The traditional concept of stress intensity factors of crack can be extended to the problem of rigid line inclusion,and they are called as the stress field intensity factors being defined as follows.

From Eq.(4.26),one can compute stress intensity factors as follows.

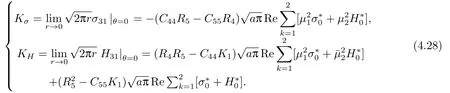
We can list the stress intensity factors as follows from Eqs.(4.21) and (4.28),

Note that GUO and his co-workers[20]have given the stress intensity factor asKIII=when the quasicrystal is subjected to the shear forcePalong the quasiperiodic direction at infinity,which is derived through solving the problem of an elliptical hole and degenerating into the problem of a Griffith crack by employing a new displacement potential function and using complex variable function method or a half-inverse method.Clearly,as in the analogous classical isotropic elastic situation[25],all the field components have been shown to exhibit acrack-tip behavior,and the present results agree with the solutions given in [20] (when their remote loadingsPare replaced byσ0andH0,respectively).So,it shows that our method is effective.

5.Conclusion

The macroscopical crack or rigid line inclusion which is placed on the periodic (x1,x2)-plane is studied for finding out the influence of phason displacement on the related physical quantities.These two models are reduced to the Riemann–Hilbert problem of generalized complex functions to obtain the closed-form solutions for antiplane mode.As a consequence,the explicit solutions of stress intensity factors are derived analytically.From the stress intensity factors with the analytical form for antiplane mode,one can find that the phonon and phason stress intensity factors of crack as well as the phonon and phason stress field intensity factors of rigid line inclusion are not related to the coupling of phonon and phason fields.These mean that there is no influence of phason displacement on both the phonon stress intensity factor of crack and the phonon stress field intensity factor of rigid line inclusion.