集值均衡与Browder变分包含问题解的存在性

张从军,鞠贵垠,王月虎

(1.南京财经大学应用数学学院,江苏 南京210046;2.南京财经大学管理科学与工程学院,江苏 南京210046)

1.引言

设C为Hausdorff拓扑向量空间中的非空子集,Y为Banach空间,P ⊂Y为锥.集值映射ϕ:C×C⇒Y,集值均衡问题如下：

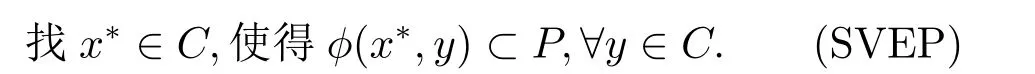
我们也可考虑弱集值均衡问题如下：

一般均衡问题为：

φ:C×C −→R为二元映射.

变分不等式问题、最优化问题、数学规划、互补问题及不动点问题等都可转化为均衡问题进行统一研究.在对均衡问题的研究中,有些会涉及映射的半连续性(如[1-3]) 在这方面,文[4]对映射的定义域加上强制性条件情况下,去掉半连续性的假设,得到了解的存在性结果.文[5]中引进了自段密集的概念,对集值均衡问题进行了推广,文[6] 中去掉集合的凸性,讨论集值均衡问题.

受以上工作的启发,本文进一步讨论集值均衡问题和变分包含问题.利用集值映射的上、下半连续性,凹凸性及Ky Fan引理,结合锥和自段密集的概念,研究了集值均衡问题解的存在性,推广了文[7]的相关结论.并将集值均衡问题解的存在性结果运用到变分包含问题之中.

2.预备知识

本文中,设X为局部凸的拓扑向量空间,Y为Banach空间.

定义2.1[1]设F:X⇒Y集值映射,F的图为

定义2.2设F:X⇒Y集值映射,对任意集合B ⊂Y,称

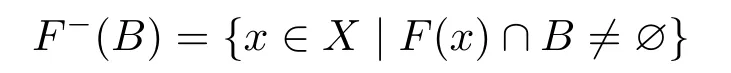
为B关于F的下原象.

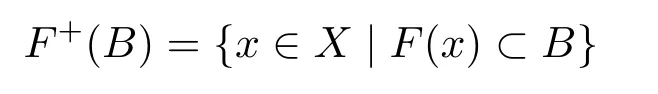
为B关于F的上原象.

定义2.3设Y为实的Banach空间,P是Y中的非空闭凸集,称P是Y中一个锥,如果满足：

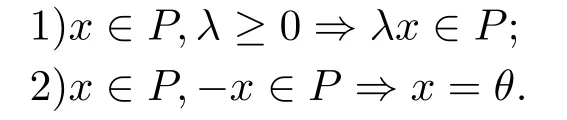
以下我们引进强锥的概念.

定义2.4设P为Y中一个锥,若对任意有限集{z1,z2,···,zn},ziP且我们有

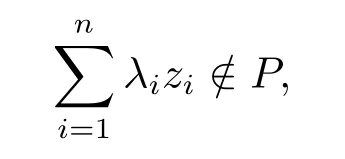
则称P是强锥.

例2.1令Y=R2,P={(x,y)|x ≥0},易验证P为一个强锥.

定义2.5设X为Hausdorff拓扑向量空间,D ⊂X,集值映射F:D⇒Y,

1)称F在D上为凸的：对任意的有限集

2)称F在D上为凹的：对任意的有限集使得

定义2.6凸集V ⊂X,U ⊂V,U为V中的自段密集,满足下列条件：

1)V ⊂cl(U);

2)∀x,y ∈U,[x,y]⊂cl([x,y]∩U).

注2.1[x,y]={λx+(1−λ)y|λ ∈[0,1]}.

引理2.1[7]设集值映射F:X⇒Y,S为X的子集,下列条件等价：

1)F在X上为下半连续;

2)对任意的开集V ⊂Y,有

3)对任意的闭集B ⊂Y,有

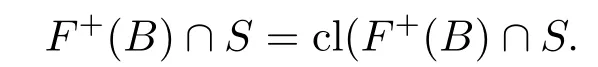
特别地,F在S上为下半连续,则对任意的开集V ⊂Y,F−(V)∩S为S中开集；对任意的闭集B ⊂Y,F+(B)∩S为S中闭集.

注2.2cl(S),int(S)分别表示S的闭包、内部.

引理2.2[7]设集值映射F:X⇒Y,S为X的子集,下列条件等价：

1)F在X上为上半连续;

2)对任意的开集V ⊂Y,有

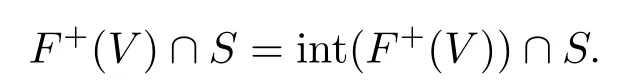
3)对任意的闭集B ⊂Y,有

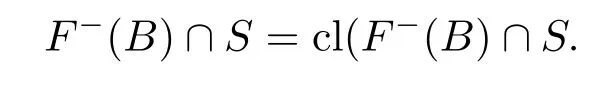
引理2.3[7]设X为局部凸的Hausdorff拓扑向量空间,凸集V ⊂X,U ⊂V为自段密集,则对任意的有限集{x1,···xn}⊂U,有cl(conv{x1,x2,···,xn}∩U=conv{x1,x2,···,xn}.

引理2.4[8]若集值映射F:N⇒X满足下列条件：

1)F为KKM映射;

2)F(x)为闭集,对任意x ∈N;

3)存在x0∈N,使得F(x0)为紧集.则有

3.集值均衡问题解的存在性

定理3.1设X为局部凸Hausdorff拓扑向量空间,C ⊂X为非空闭凸集,D ⊂C为自段密集.Y为Banach空间,P ⊂Y为强锥,集值映射ϕ:C×C⇒Y,满足下列条件：

1)∀x ∈D,ϕ(x,x)⊂P;

2)(x,y) 为凸的在D上;

3)(x,y)为下半连续在CD;

4) 存在紧集K ⊂C,y0∈D使得

5)(x,y) 为下半连续在K上.

则集值均衡问题(SVEP)有解.

证设集值映射ϕ+:C⇒C,其中ϕ+(y)={x ∈C|ϕ(x,y)⊂P},∀y ∈C.则x0∈C为集值均衡问题(SVEP)的解当且仅当由条件1)ϕ+(y)∅,∀y ∈D.令集值映射cl(ϕ+) :D⇒C,其中cl(ϕ+)(y)=cl(ϕ+(y))=cl({x ∈C|ϕ(x,y)⊂P}),∀y ∈D.显然cl(ϕ+(y))为闭集,由条件4)可得∀y ∈D,cl(ϕ+(y0))为K中的紧集.

下面证明cl(ϕ+):D⇒C为KKM映射.

对任意有限集{y1,y2,···,yn} ⊂D,设利用条件1)与条件2)则有

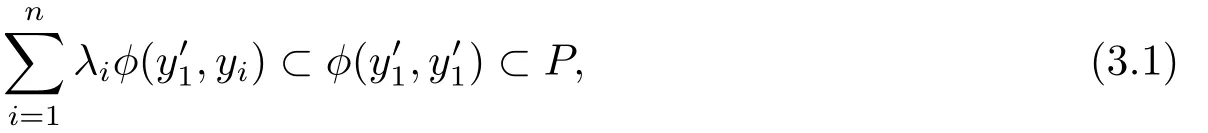
则必存在i0∈{1,2,· · ·,n},使得ϕ(y′1,yi0)⊂P.反证法,若对∀i,ϕ(y′1,yi)则存在zi∈ϕ(y′1,yi) 且ziP.由(1.1)式,有与P为强锥矛盾.所以∃i0使得ϕ(y′1,yi0)⊂P有

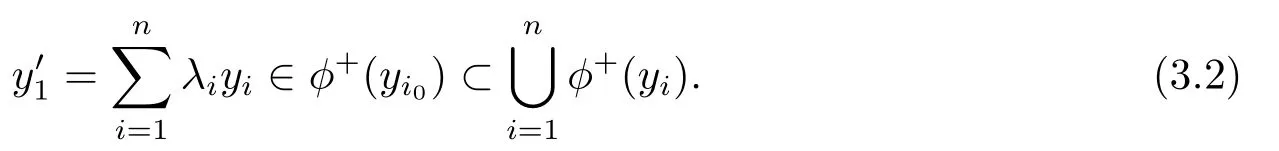
若y′1,即y′1∈CD,则有

由引理2.3,有

所以集值映射cl(ϕ+)为KKM映射.

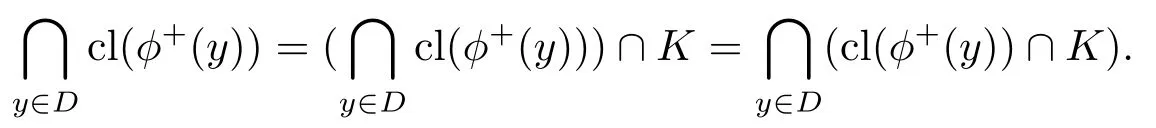
由条件5)cl(ϕ+(y))∩K,因为y0∈D,ϕ+(Y0)⊂K,所以从而有因此存在x0∈C,使得

下面我们推广到C上.令y ∈C D,D ⊂ϕ+(x0,P)={y′∈C|ϕ(x0,y′)⊂P}.D在C上稠密,y ∈C ⊂cl(D)⊂cl(ϕ+(x0,P)),有

由条件3)可得到y ∈cl(ϕ+(x0,P))∩(CD)=ϕ+(x0,P)∩(CD),因此

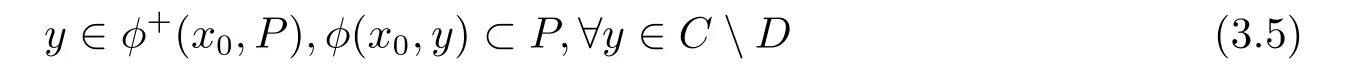
结合(3.4)与(3.5),所以∃x0∈C,使得ϕ(x0,y)⊂P,∀y ∈C.

注3.1在定理3.1中,令Y=R,P=R+即是文[7]中定理3.1(见下面推论3.1),因此我们这里把实数情形的结论推广到锥的形式.

推论3.1设X为局部凸Hausdorff拓扑向量空间,C ⊂X为非空闭凸集,D ⊂C为自段密集.集值映射ϕ:C×C⇒R,满足下列条件：

1)∀x ∈D,ϕ(x,x)⊂R+;

2)(x,y) 在D上为凸的;

3)(x,y) 在CD为下半连续;

4)存在紧集K ⊂C,y0∈D,使得

5)(x,y) 在K上半连续.则存在x∗∈C,使得ϕ(x∗,y)⊂R+,∀y ∈C.

下面讨论弱集值均衡问题解的存在性.

定理3.2设X为局部凸Hausdorff拓扑向量空间,C ⊂X为非空闭凸集,D ⊂C为自段密集.Y为Banach空间,P ⊂Y为强锥.集值映射ϕ:C×C⇒Y,满足下列条件：

1)∀x ∈D,ϕ(x,x)∩P∅;

2)(x,y) 在D上为凹的;

3)(x,y) 在CD上半连续;

4)存在紧集K ⊂C,y0∈D,使得ϕ(x,y0)⊂(−P {θ}),∀x ∈CK;

5)(x,y) 在K上半连续.

则弱集值均衡问题(SVEP(W))有解.

证设集值映射ϕ−:C⇒C,其中ϕ−(y)={x ∈C|ϕ(x,y)∅},∀y ∈C.则x0∈C为弱集值均衡问题(SVEP(W))的解当且仅当

令集值映射cl(ϕ−) :D⇒C,其中cl(ϕ−)(y)=cl(ϕ−(y)),∀y ∈D.由条件(1),ϕ−(y)∅,∀y ∈D,显然cl(ϕ−)(y)为闭集,由条件4)可得cl(ϕ−)(y0) 为K中的紧集.

下证明cl(ϕ−):D⇒C为KKM映射.

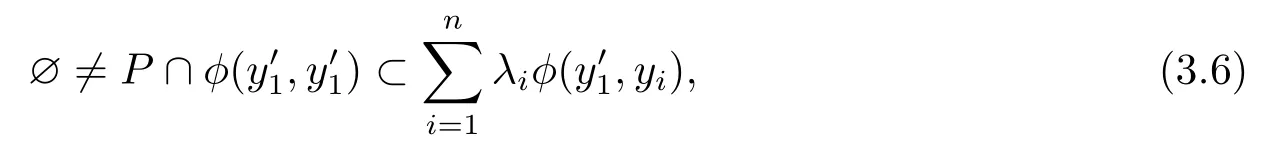
则必存在i0∈{1,2,···,n},使得ϕ(y′1,yi0)∅.利用反证法,若∀i,ϕ(y′1,yi)∩P=∅.∀zi∈ϕ(y′1,yi)且ziP.由P为强锥.对任意zi,与(3.6)式矛盾.因此存在∃i0,使得ϕ(y′1,yi0)∅.由对任意的有限集所以

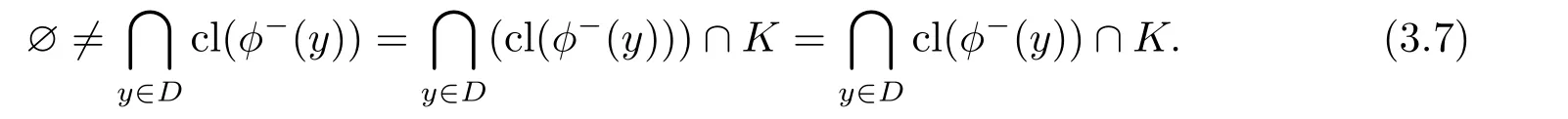
由条件5),ϕ−(y)∩K=cl(ϕ−(y))∩k,y0∈D,ϕ−(y0)⊂K,所以有

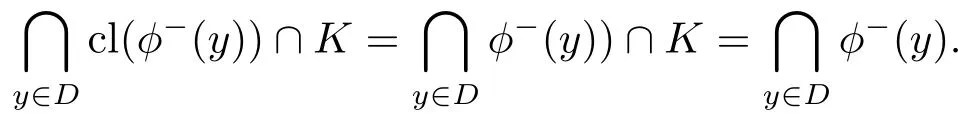
下面我们推广到C上.∀y ∈CD,设所以D ⊂ϕ−(x0,P).因为D在C上稠密,我们有

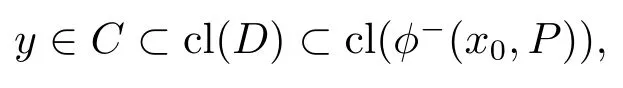
因此y ∈cl(ϕ−(x0,P))∩(CD).根据条件3),

所以y ∈ϕ−(x0,P),即ϕ(x0,y)∅,∀y ∈CD结合(2.3)式,可得到ϕ(x0,y)∅,∀y ∈C.

注3.2令Y=R,P=R+,即可得到文[7]中定理3.2,也就是我们这里的推论3.2.

推论3.2设X为局部凸Hausdorff拓扑向量空间,C ⊂X为非空闭凸集,D ⊂C为自段密集.集值映射ϕ:C×C⇒R,满足下列条件：

1)∀x ∈D,ϕ(x,x)∩R+∅;

2)(x,y) 在D上为凹的;

3)(x,y)在CD上半连续;

4) 存在紧集K ⊂C,y0∈D,使得ϕ(x,y0)⊂R∗−,∀x ∈CK;

5)(x,y)在K为上半连续.则存在x∗∈C,使得ϕ(x∗,y)∩R+∅,∀y ∈C.

4.应用

本节,我们给出Browder变分包含解的存在性及应用.变分包含问题作为变分不等式的推广,已经在文[9-11]中研究,下面将文献中的结果进行了相应的推广.

X为赋范线性空间,X∗为X的对偶空间,Y为Banach空间,A ⊂X∗,我们定义⟨A,x⟩={⟨x∗,x⟩|x∗∈A},B(X,Y)表示X到Y全体有界线性泛函,B∗(X,Y)为B(X,Y)上的所有线性泛函.

定理4.1设X为赋范线性空间,C ⊂X为非空闭凸集,Y为Banach为空间,P ⊂Y为强锥.集值映射F:C⇒B(X,Y),满足下列条件：

1) 存在紧集K ⊂C,y0∈C,使得

2)F在K上半连续;

3)F在K上为弱紧集;

4)∀φ ∈B∗(X,Y),存在f ∈Y ∗,x ∈X,使得φ(T)=f(T(X)),∀T ∈B(X,Y).则存在x0∈K,使得⟨

证易验证满足定理3.2条件1),3),4).下证明满足定理3.2条件2).设有限集{y1,···,yn}⊂C,且我们有

有x的任意性,所以因此,

下证明满足定理3.2条件5).固定y ∈D,V为Y中开集,令先证明存在δ >0,使得

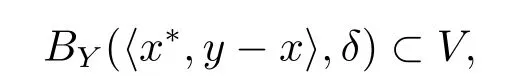
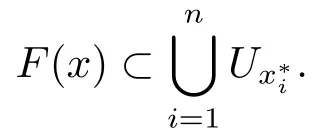
取δ=min1≤i≤nεx∗i,若则存在i=1,· · ·,n.所以再令

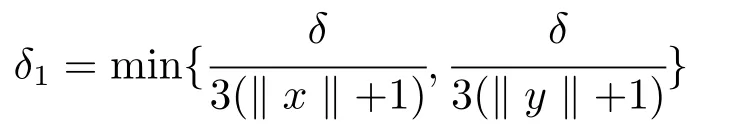
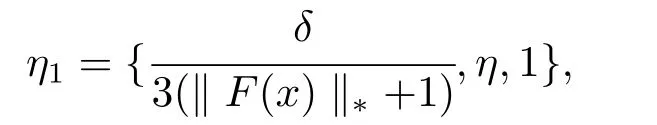
其中∥F(x)∥∗=max{∥x∗∥∗|x∗∈F(x)},设U=BX(x,η1)∩C.下证明∀z ∈U,ϕ(z,y)⊂V.我们设z ∈U,z∗∈F(z),∃x∗0∈F(x),使得z∗∈F(z)⊂BB(X,Y)(x∗0,δ1).则有

注4.1我们考虑特殊情形,令Y=R,P=[0,+∝),得到下面的推论4.1.

推论4.1设X为赋范线性空间,C ⊂X为非空闭凸集,X∗为X的对偶空间.集值映射F:C⇒X∗满足:

2)F在K上半连续;

3)F在K上为f∗紧值的.

则存在x0∈K,使得