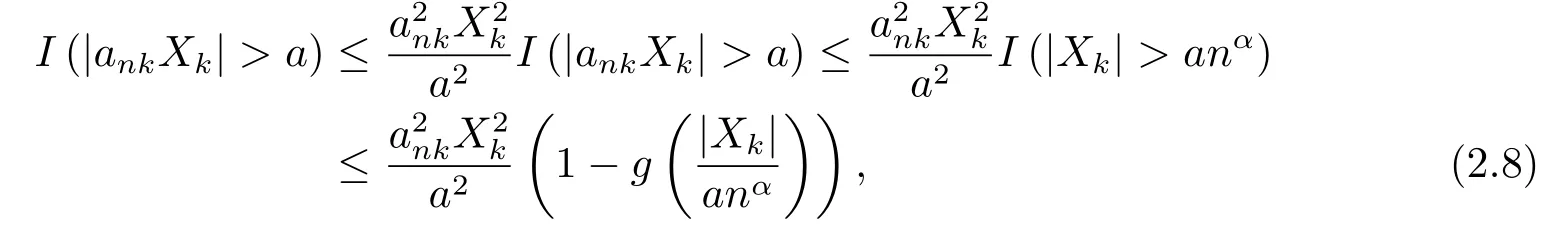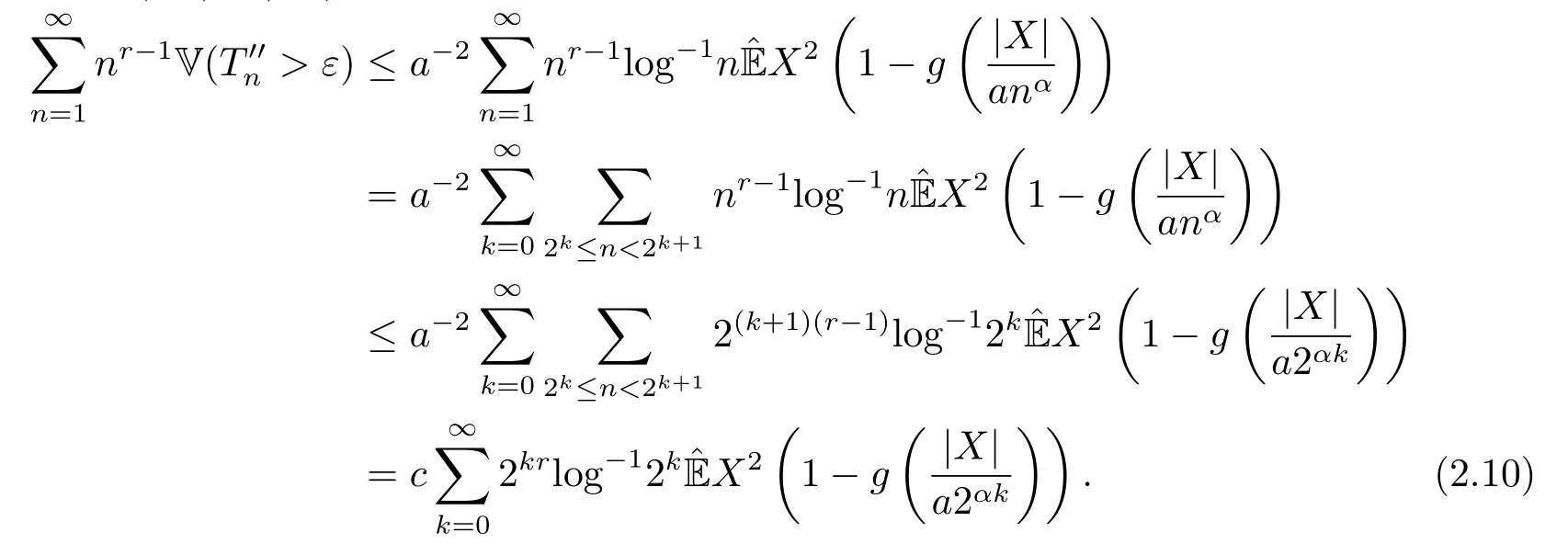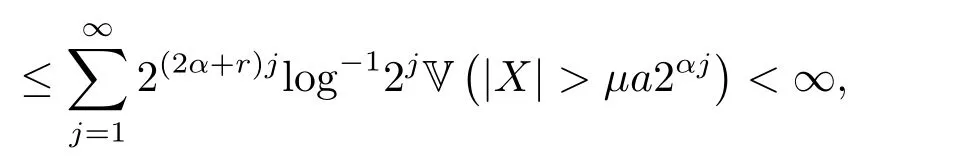次线性期望空间下END列加权和的完全收敛性

马晓晨,吴群英

(桂林理工大学理学院,广西 桂林541004)

1.引言及引理

极限理论是概率论和统计学中的重要研究课题,它们被广泛运用到金融领域和其他领域中.经典极限理论只在模型确定的情况下成立.然而,这样的模型确定性假设在实践中许多应用领域是不成立的,因为不确定性现象无法用确定性模型解释.因此,彭实戈院士[1]引入了次线性期望空间理论,并给出了次线性期望理论的完整公理体系.由于次线性期望为次线性概率问题提供了一个灵活的框架,所以次线性期望下的极限理论近年来受到越来越多学者的关注和研究.目前,已经取得了一系列有用的结果.如PENG[2]证明了次线性期望空间下的中心极限定理; ZHANG[3−5]得到了次线性期望下广义ND的Kolmogorov强大数定律、矩不等式、重对数率以及独立和ND情况下的Rosenthal’s不等式; WU和JIANG[6]得到了次线性期望空间下的强大数律与Chover’s型重对数律,HU[7]证明了次线性期望空间下一般矩条件的强大数律,ZHONG和WU[8]研究了次线性期望下的END列加权和的完全收敛和完全积分收敛等.完全收敛性的概念最早是由HSU和ROBBINS[9]引入的,并证明了如果随机变量的方差是有限的,则独立同分布随机变量的算术平均序列收敛到期望值.目前,完全收敛性在概率空间下已经有了很深入的研究,如WU[10−11]分别给出了ND序列和ND阵列随机变量完全收敛性的证明; 孟兵和吴群英[12]证明了ND阵列加权乘积和的完全收敛性等等.一般来说,将传统概率空间的极限理论推广到次线性期望空间的情形是可取的,在理论上和应用上都有重要意义.目前在次线性期望空间下随机变量序列的完全收敛性的相关论文还很少,本文在现有的理论基础上,进一步将文[13]中定理2.1从概率空间中NOD列加权和的完全收敛性推广到了次线性期望空间下END列加权和的完全收敛性,并且在更优的条件下得到了比文[14]更强的结果.

我们引用彭实戈院士[1−2]提出的次线性期望空间的框架,假设(Ω,F)是给定的可测空间,H是定义在(Ω,F) 上由实函数构成的线性空间,对任意X1,X2,··· ,Xn∈H,φ ∈Cl,Lip(Rn),都有φ(X1,X2,··· ,Xn)∈H,其中Cl,Lip(Rn)表示在线性空间的局部Lipschitz函数,即对任意φ ∈Cl,Lip(Rn),存在常数c>0,m ∈N取决于φ,都有

也称H是由随机变量所构成的空间,并记X ∈H.

定义1.1[4]称:H →为次线性期望,如果对任意X,Y ∈H,都有以下性质:

1) 单调性: 如果X ≥Y,那么

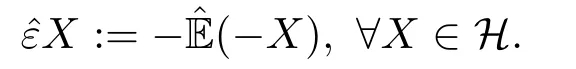
定义1.2[4]令G ⊂F,一个函数V:G →[0,1]称为容度,如果

1)V(∅)=0,V(Ω)=1;

2) 对任意A ⊂B,A,B ∈G,则有V(A)≤V(B).

如果对所有的A,B ∈G,都有V(A ∪B)≤V(A)+V(B),则称V具有次可加性; 如果对任意An∈F,有则称V具有可数次可加性.

在次线性空间(Ω,H,),定义上容度和下容度(V,V),即对任意A ⊂F,

其中,Ac为A的补集.由定义可知,V具有次可加性,且对任意f ≤I(A)≤g,f,g ∈H,有

定义1.3[4]Choquet积分为

可以用V代替V得到相应的积分.

定义1.4[4](同分布) 假设X1,X2是定义在次线性期望空间(Ω1,H1,)和(Ω2,H2,)上的随机变量,如果(φ(X1))=(φ(X1)),∀φ ∈Cl,Lip(R),则称其为同分布的,记为X1

d=X2.如果对则称{Xn;n ≥1}是同分布的序列.

定义1.5[3](END序列) 在次线性空间(Ω,H,ˆE)下,如果存在常数K ≥1,使得下面式子成立

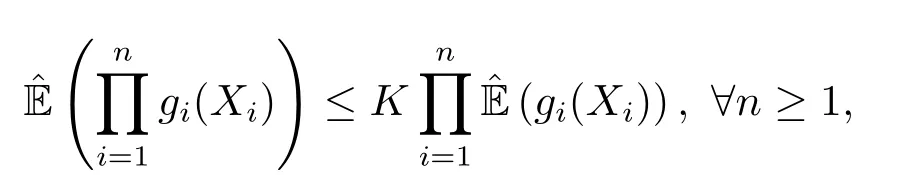
其中,非负函数gi∈Cl,Lip(Rn),i=1,2,···,是非降(或非增)的,则称随机变量序列{Xn;n ≥1}为END序列.

显然,由END随机变量序列的定义,我们可以得出,如果{Xn;n ≥1}是END随机变量序列,以及f1(x),f2(x),··· ,∈Cl,Lip(Rn)是非降（或非增）的函数,那么{f(Xn);n ≥1}也是一个END随机变量序列.

在本文中,符号c始终代表一个正的任意常数,在不同的地方取不同的值;an∼bn表示limn→∞an/bn=1;I(·)表示示性函数.

为证本文的结论，我们需要以下3 个引理.

引理1.6(Markov不等式)∀X ∈H,有

证对于∀x>0,p>0,因为

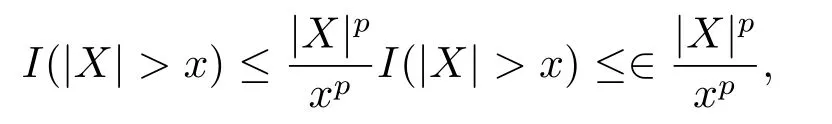
引理1.7[14]设X是次线性空间(Ω,H,)下的随机变量,满足X ≤1,则

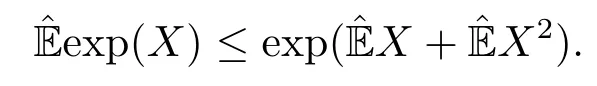
引理1.8假设X ∈H,r >0,α>0,则对于任意c>0,有

证令对任意c>0,记c1=c2+r/αln2(2α+r),Z−1(x)是Z(x)的反函数,根据Choquet 积分的定义,我们有

因此,

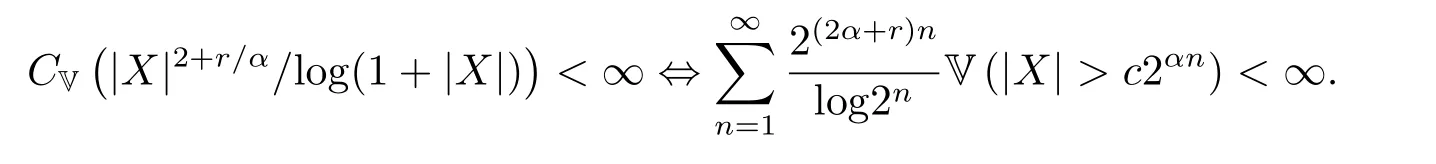
2.主要结果及其证明

定理2.1假设{X,Xn;n ≥1}是次线性期望空间(Ω,H,)下的同分布END随机变量序列,具有可数次可加性,{ank;k ≥1,n ≥1}是正常数阵列,满足supk≥1ank≤cn−α.如果r >0,α>0,且

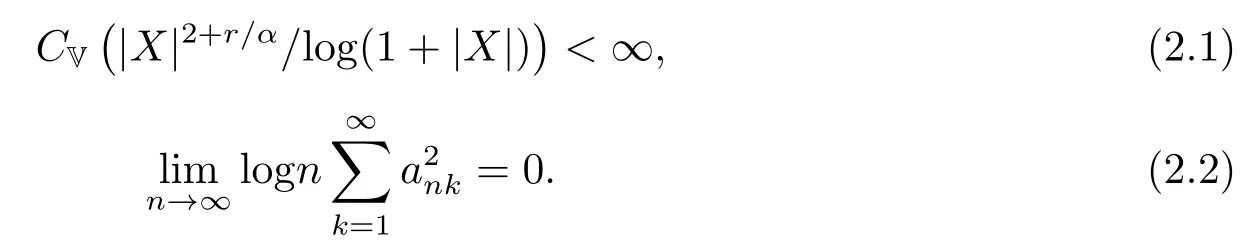
则

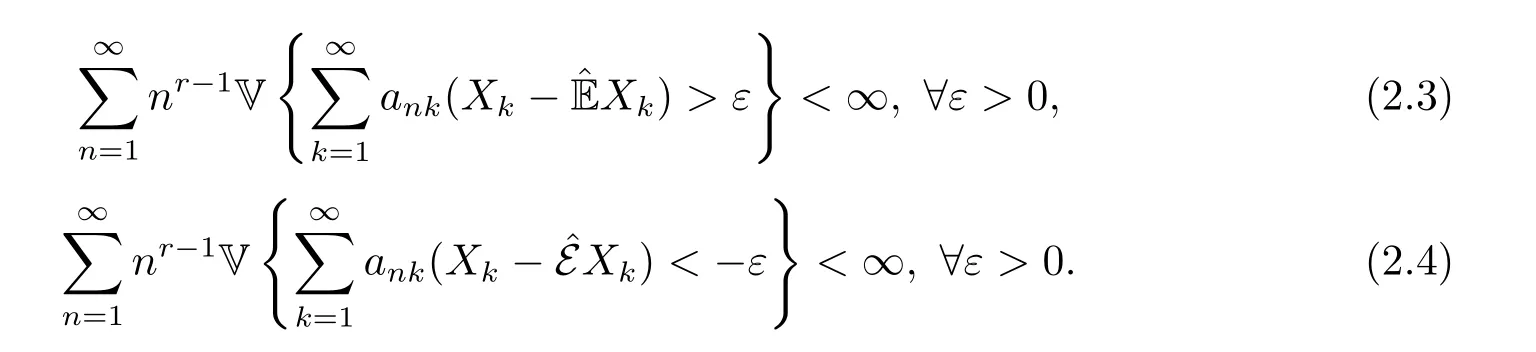
注定理2.1是将文[13]中定理2.1从概率空间推广到了次线性期望空间.

证不失一般性,我们可以假设Xn=0,根据(2.1)式以及上期望具有可数次可加性,有所以可假设对于任意k ≥1,n ≥1都成立.令

由于{X,Xn;n ≥1}是一个END序列,为了确保截尾随机变量也是END序列,则需要使截尾后的序列属于Cl,Lip并且为非增(非减)的.给定任意ε >0,取ρ >0,正整数N.因为n−ρ→0,n →∞,所以对于任意给定的ε,N,存在正整数N0使得当n ≥N0时,有n−ρ<ε/N.因为本文结论证明的是完全收敛性,又由于完全收敛性与前面有限项是无关的,所以可以不妨假设当n ≥1时,n−ρ<ε/N.记

由定义1.5 知,{ankX′nk,k ≥1}是END序列,进而知{exp(unankX′nk),k ≥1}也是END序列,其中,un=min(ε/2cn,nρ),记并且有

因unankX′nk≤1,由引理1.7知,又因为因此有及由引理1.6有

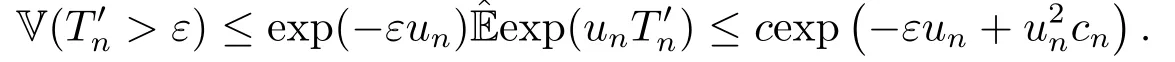
如果ε/2cn>nρ,则由un的定义有V(T′n>ε)≤cexp(−εnρ/2),

如果ε/2cn≤nρ,则有V(T′n>ε)≤cexp(−ε2/4cn).

对于∀r >0,ε >0,ρ >0,由limn→∞nr+1/exp(εnρ/2)=0,可知nr/exp(εnρ/2)=o(1/n),当n充分大时,有nr/exp(εnρ/2)≤1/n,则有

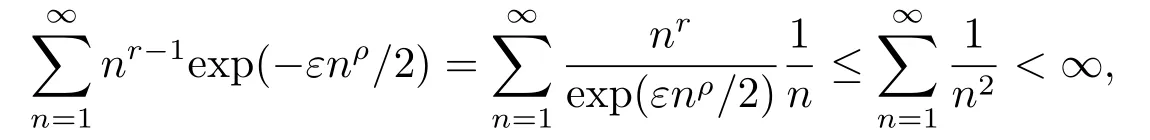
由(2.2)式知cn=o(1/logn),所以,对δ=ε2/4(r+1)>0,当n充分大时,有cn≤δ/logn,即1/cn≥logn/δ,则有

于是有

假设函数g(x)∈Cl,Lip(R),是一个偶函数,并且在(0,∞)上是单调下降的,使得∀x ∈R,0≤g(x)≤1; 且当|x|≤µ(0<µ<1),g(x)=1; 当|x|>1,g(x)=0.则有

记a=ε/N,对任意n ≥1,k ≥1,根据ank

则根据同分布序列,由(2.7)和(2.8)有

于是,由(2.2)和(2.9)式可得,

再取函数gj(x)使gj(x)∈Cl,Lip(R),且对任意x有0≤gj(x)≤1,其中j ≥1,且当a2αj≤|x|

则有

由的定义,如果如果n−ρ< ankXk≤ε/N,则因此为使至少存在N个下标使取2

因此,取0<ρ<α(p −2)/P,N >r/α(p −2)−ρp,我们有

结合(2.6),(2.12)和(2.13)式便证明完式子(2.3).显然,{−X,−Xn;n ≥1}也满足定理2.1中的条件,用{−X,−Xn;n ≥1}替换(2.3)中的{X,Xn;n ≥1}有

这便得到了式子(2.5),即完成了定理2.1的证明.