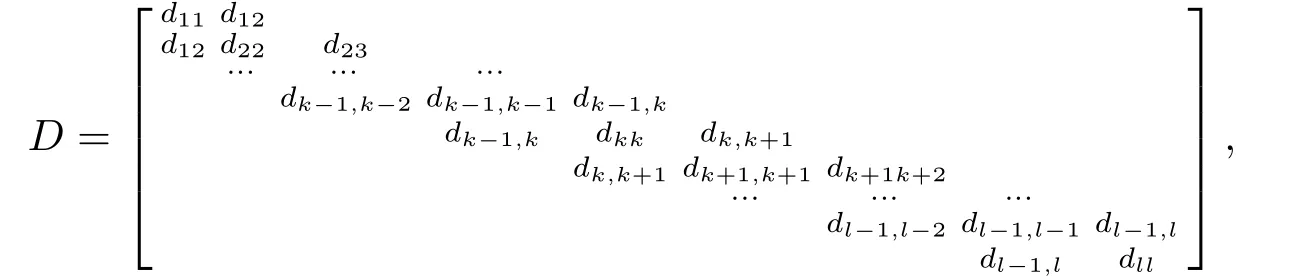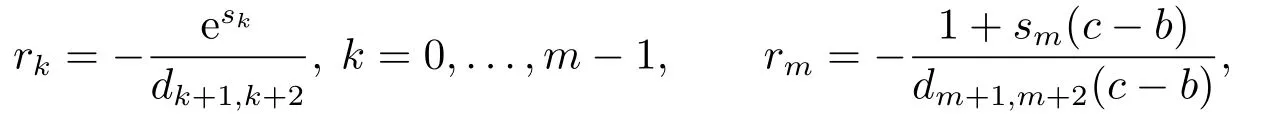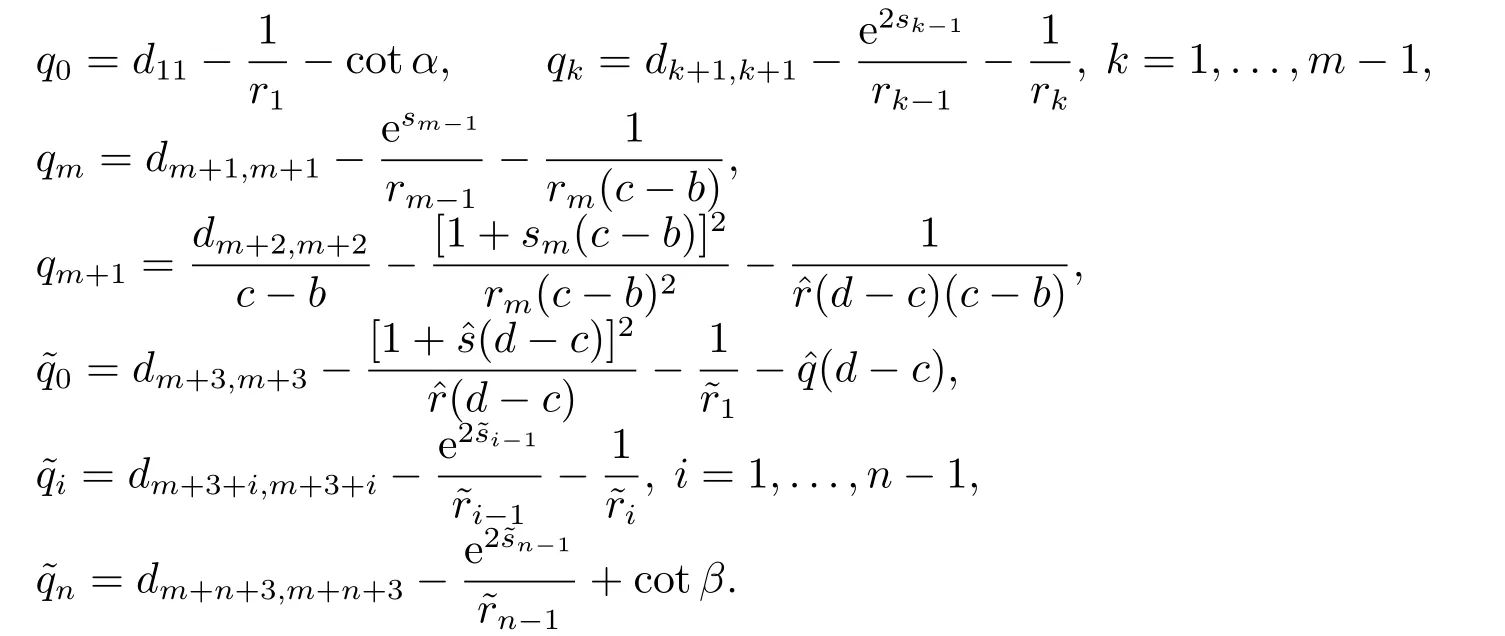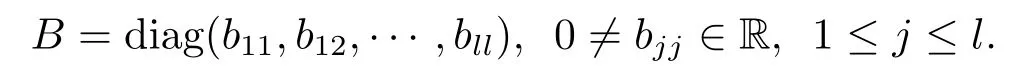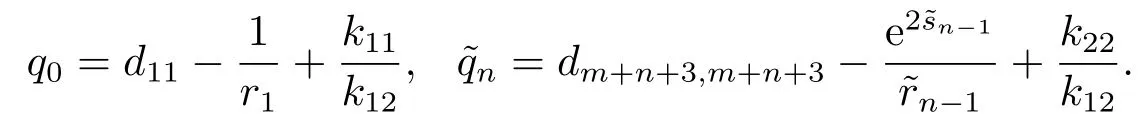时标上具有分布势函数的Sturm-Liouville问题的矩阵表示
刘娜娜,敖继军
( 内蒙古工业大学理学院,内蒙古 呼和浩特010051)
1.引言
近年来,关于Sturm-Liouville(S-L)问题的特征值问题已经成为数学物理等领域研究的热门课题,并取得了许多成果[1].早在1964年,Atkinson提出了二阶S-L问题在某些条件下存在有限谱的论断[2].2001年KONG,WU和Zettl运用构造的方法证实了Atkinson论断的合理性[3].由此学者们对有限谱问题展开了一系列研究.2009年KONG,Volkmer,Zettl分别在分离型和实耦合型自共轭边界条件下研究了具有有限谱的S-L问题的矩阵表示[4].2011年,AO,SUN,ZHANG讨论了带有转移条件的S-L问题的有限谱[5].2017年,敖继军,薄芳珍给出了带谱参数边界条件的四阶边值问题的矩阵表示的结论[6].
为了找到一种能够将离散和连续两者结合起来,将微分方程和差分方程结合起来的理论框架,1988年,德国数学家Stefan Hilger在他的博士论文中首次提出了时标的概念.所谓时标(测度链)就是指实数集R的任一非空闭子集,它可以把连续理论和离散理论融合在一起研究.如今,时标理论已经基本完善,许多学者对时标上的S-L问题从多个方面进行了一系列研究[7−12].1999年,Agarwal等在文[7]中讨论了p=1时二阶S-L问题在分离型边界条件下特征值的存在性以及特征值广义零点的个数.随后KONG将他们的结论推广到了分离型边界条件下一般的S-L问题上,并讨论了特征值的依赖性[8].2010年,XIE 等在文[9]中运用不动点原理研究了时标上高阶微分方程边值问题正解的存在性.2013年,赵娜在文[10]中考虑了二阶S-L问题的有限谱,分别讨论了分离型和耦合型S-L问题的有限个特征值,给出了其特征值不等式,并将结论推广到较一般的时标上.2016年,Tuna[11]研究了时标上二阶耗散S-L问题的完备性.
从目前的研究现状可以看出,学者们在S-L问题的有限谱,S-L问题的矩阵表示,具有分布势函数的S-L问题,时标上S-L问题的特征值等问题方面已经取得了很多理论成果.文[12]将以上问题进行了推广,讨论了时标上具有分布势函数且边界条件带有谱参数的S-L问题的有限谱.但是对于时标上具有分布势函数的S-L问题的矩阵表示还尚未见有结论.本文利用文[10]的方法,也是通过分割时标T得到了时标上具有分布势函数的二阶S-L问题的矩阵表示.
本文考虑时标上具有分布势函数的S-L问题与矩阵特征值问题

之间的等价关系,其中D和B是n ×n复值矩阵,B是对角矩阵.讨论以下具有分布势函数的S-L方程[12]:
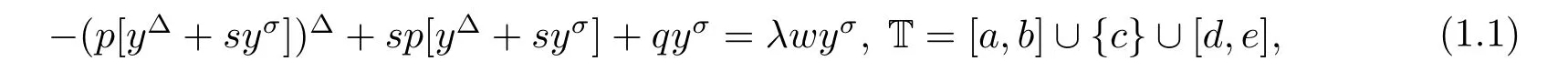
其中−∞ 考虑边界条件 且2×4矩阵(A|B)是满秩的, 本文将自共轭边界条件(1.3)分为两种类型来讨论: 分离型和实耦合型.分离型边界条件为: 实耦合型边界条件为: 因y[1]=p[y∆+syσ],则方程(1.1)可表示为: 令z=y[1],则方程(1.6)等价于 从而讨论方程(1.1)的矩阵表示问题可转化为讨论方程(1.7)的矩阵表示问题. 这部分内容将给出本文的主要结论,首先给出两个定义. 定义2.1[13]时标上具有分布势函数的S-L方程(1.1)称为是Atkinson类型的,如果对于任意的正整数m,n ∈N+,存在对时标T的分割: 使得 以及 定义2.2[4]时标上Atkinson类型的S-L问题称为是与矩阵特征值问题等价的,如果它们具有相同的特征值. 接下来再对一些符号进行说明,令 对方程(1.7)的解y,z,由条件可知: y在[a2k,a2k+1),k=0,1,...,m上为常数, 现假设 并令 引理2.1[13]对方程(1.7)的任何一组解y,z有 相反,对于系统(2.7)-(2.13)的任何一组解yk,k=0,1,...,m,zk,k=0,...,m+1和,i=0,1,...,n,,i=0,...,n+1,以及存在方程组(1.7)的唯一解y(t)和z(t)满足(2.5)和(2.6). 下面说明时标上具有分布势函数的S-L问题在边界条件(1.3)下的矩阵表示,首先讨论分离型边界条件(1.4)的情形. 定理2.1若α ∈[0,π),β ∈(0,π],定义(m+n+3)×(m+n+3)三对角矩阵 及对角矩阵 则时标上具有分布势函数的S-L问题(1.1),(1.4)与矩阵特征值问题 推论2.1(i)若α,β ∈(0,π),定义(m+n+3)×(m+n+3)三对角矩阵 及对角矩阵 则时标上具有分布势函数的S-L问题(1.1),(1.4)与矩阵特征值问题 (ii) 若α=0,β ∈(0,π),对于矩阵Rαβ,Qαβ,Wαβ也有类似结论.只是在(2.15),(2.16)中当α=0时,sinα=0,y0=0,所以矩阵Rαβ,Qαβ,Wαβ的第一行,第一列在(2.14)中消失,变为m+n+2阶矩阵,由于sin0,因此在各矩阵最后一行中除以sinβ即可.此时恰有m+n+2个特征值. (iii)若α ∈(0,π),β=π,则sinβ=0,=0,所以矩阵Rαβ,Qαβ,Wαβ的最后一行,最后一列在(2.14)中消失,变为m+n+2阶矩阵,由于sin0,因此在各矩阵第一行中同除以sinα即可.此时恰有m+n+2个特征值. (iv)若α=0,β=π,此时sinα=sinβ=0,且y0==0,所以矩阵Rαβ,Qαβ,Wαβ的第一行,第一列,最后一行,最后一列在(2.14)中消失,变为m+n+1阶矩阵,此时恰有m+n+1个特征值. 以下再来讨论实耦合型边界条件(1.5)的情形.我们分k12=0和k120两种情形给出定理. 定理2.2当k12=0时,定义(m+n+2)×(m+n+2)矩阵 及对角矩阵 则时标上具有分布势函数的S-L问题(1.1),(1.5)与矩阵特征值问题 定理2.3当(1.5)中k120时,定义(m+n+3)×(m+n+3)矩阵 及对角矩阵 则时标上具有分布势函数的S-L问题(1.1),(1.5)与矩阵特征值问题 若系数满足条件(1.2),(2.2)和(2.3),以下结果说明了具有分布势函数的S-L问题(1.1),(1.3)与以分段常值函数为系数的S-L问题等价. 定理2.4[13]设qk,wk,k=0,1,...,m,,,i=0,1,...,n及rk,sk,k=0,1,...,m −1,,,i=0,1,...,n−1由(2.2),(2.3)给出.定义时标T上的分段常值函数如下: 当sk=0,=0时; 且满足边界条件(1.3),则具有分布势函数的S-L问题(1.1),(1.3)与以分段常值函数为系数的方程和边界条件(1.3)构成的S-L问题具有相同的特征值. 这部分内容将给出本文主要定理的证明过程,在证明过程当中用到的有关时标的定义可参见文[10]. 定理2.1的证明由边界条件(1.4)可知 首先容易得出问题(2.7)-(2.13),(3.1)的解与以下问题的解是一一对应的: 事实上,若假设yk,k=0,1,2,...,m和zk,k=0,1,2,...,m+1是系统(2.7)-(2.9),(3.1)的解.则(3.2)-(3.4)可由(2.7)-(2.9)得出.同理,(3.6)-(3.8)可由(2.11)-(2.13)通过假设,i=0,1,2,...,n和,i=0,1,2,...,n+1为系统(2.11)-(2.13)的一组解而得到.(3.5)可由(2.10)通过假设,为问题(2.10)的解而得到.其中 另一方面,若设yk,k=0,1,2,...,m是系统(3.2)-(3.4)的一组解,则z0和zm+1可分别由(3.1),(3.2)和(3.4)定义得出,由(2.7)可定义zk,k=1,2,...,m,然后利用(3.2)-(3.4)进行逐步推导即可得(2.8),(2.9),同理可得(2.11)-(2.13).因此由引理2.1,方程(1.7)的任何解,从而也是方程(1.1)的解,被系统(3.1)-(3.8)的解唯一决定.故由(3.1)-(3.8)可得两类问题之间的等价性. 定理2.2的证明当k12=0时,边界条件(1.5)可以写为 其中k11k22=1,即可得到方程组(2.7)-(2.13)与边界条件(3.9)所构成的问题的解与问题(3.2)-(3.8)的解是等价的,其中方程(3.2)与(3.8)变为以下两式: 由(2.7)-(2.9),(3.9)可得: 又因为k11k22=1,所以(3.12)可写作(3.10).剩下的证明过程类似定理2.1的证明过程. 定理2.3的证明当时,边界条件(1.5)可以写为 其中k11k22−k12k21=1,即定理2.2的证明过程当中(3.10),(3.11)式变为 剩下的证明过程类似定理2.2的证明,这里就不再重复了. 该部分内容讨论矩阵特征值问题 的具有分布势函数的S-L问题表示,其中,对称矩阵D=(dij)是l×l实三对角矩阵或“几乎”三对角矩阵,且满足di,i+10,i=1,2,...,l −1,对角矩阵B=(bjj)满足bjj0.由定理2.4可知这种表示并不唯一.接下来利用S-L问题(2.25),(1.3)及其等价类来描述矩阵问题(4.1)的S-L问题表示,这里仅以分离型边界条件为例,对于实耦合型边界条件情形可用同样方法得出. 定理4.1设D是l×l对称三对角矩阵 其中l>3,2≤k ≤l −2,dij∈R,1≤i,j ≤l,且dj,j+10,j=1,...,l −1,并设 1)α,β ∈(0,π),且sk,k=0,...,m −1,,i=0,...,n −1 是固定的; 2)α=0,β ∈(0,π),r1,q0,w0与sk,k=0,...,m −1,,i=0,...,n −1是固定的; 3)α ∈(0,π),β=π,与sk,k=0,...,m −1,,i=0,...,n −1是固定的; 4)α=0,β=π,r1,q0,w0,与sk,k=0,...,m −1,˜si,i=0,...,n −1是固定的. 在以上任一种情形下,矩阵问题(4.1)的所有S-L问题表示均可以由S-L问题(2.25),(1.4)及其等价类按照对参数的任何可能的选取形式给出. 证考虑α,β ∈(0,π)的情形.令m=k −1,n=l −k −2,T=[a,b]∪{c}∪[d,e],−∞ 且 然后,再利用(2.20)-(2.24)在时标T=[a,b]∪{c}∪[d,e]上定义满足(2.2)-(2.4)的分段常值函数显然(4.1)和问题(2.15)具有相同的形式.故由推论2.1可知问题(4.1)和具有分布势函数的S-L问题(1.1),(1.4)是等价的.其它情形证明过程类似. 定理4.2设D是l×l对称矩阵 其中l>3,2≤k ≤l −2,dij∈R,1≤i,j ≤l,且dj,j+10,j=1,...,l −1,d1l0,并设 1)k120,且sk,k=0,...,m −1,,i=0,...,n −1是固定的; 2)k12=0,且q0,w0,sk,k=0,...,m −1,,i=0,...,n −1是固定的. 在以上任一种情形下,矩阵问题(4.1)的所有S-L问题表示均可以由S-L问题(2.25),(1.5)及其等价类按照对参数的任何可能的选取形式给出. 证考虑k120的情况,将(4.1)乘以(k11d1l)−1,可得矩阵D满足令m=k −1,n=l −k −2,T=[a,b]∪{c}∪[d,e],−∞< a < b < c < d < e < ∞,根据(2.1)的一个分割,可类似定理4.1的方法进行证明,与之不同的是 对于k12=0的情形,也可用同样的方法得到结论. 注4.1文[13]探究了连续区间J=(a,b)上具有分布势函数的S-L问题的矩阵表示,而本文是在时标T=[a,b]∪{c}∪[d,e]上讨论了具有分布势函数的S-L问题的矩阵表示,可将连续系统与离散系统有效地结合起来.其中的难点在于要找到离散点和连续区间的端点-也就是c点与两个连续区间[a,b],[d,e]中b点和d点之间的连接矩阵及迭代公式,这也是与连续区间上同类问题之间的主要区别之处.在证明过程中,解决问题的关键是要通过两个连接矩阵,找到离散点c点与b点,d点之间的连接方程.当时标取为区间时,本文结论将退化为连续区间上具有分布势函数的S-L 问题,即文[13]中结论,进一步如果s=0,则本文结论又可退化为经典的S-L问题的矩阵表示问题,即文[4]的结论.

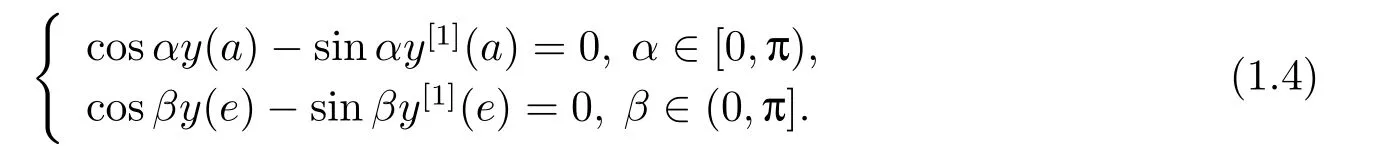
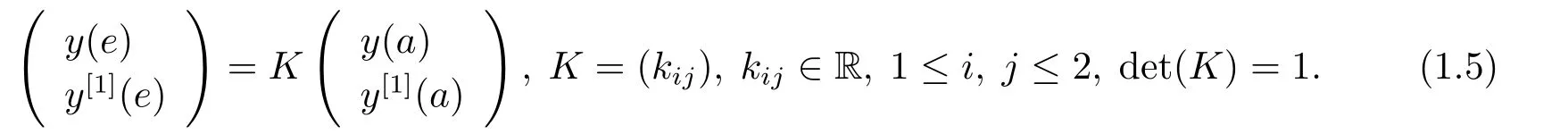

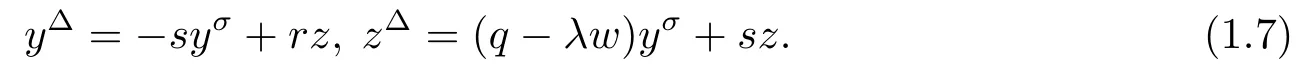
2.主要结论
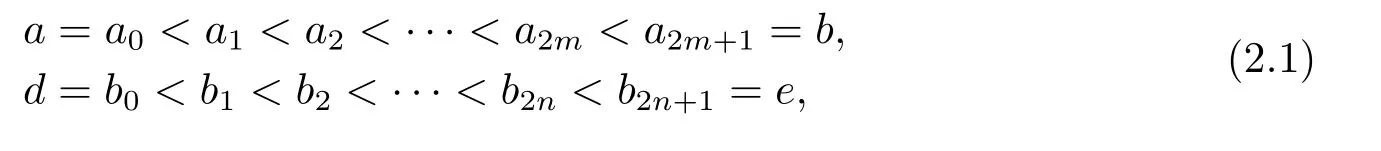


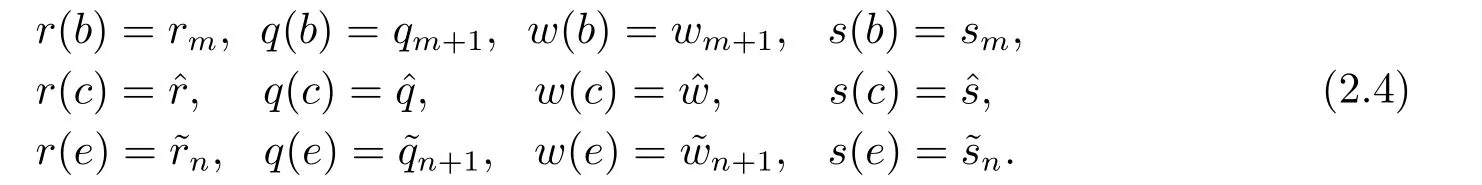
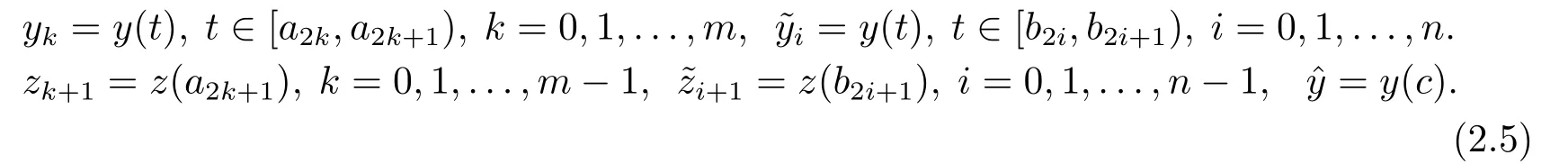
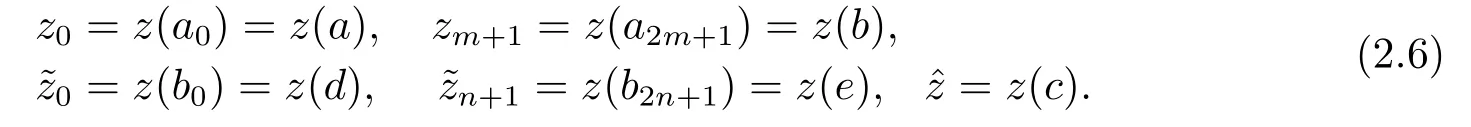
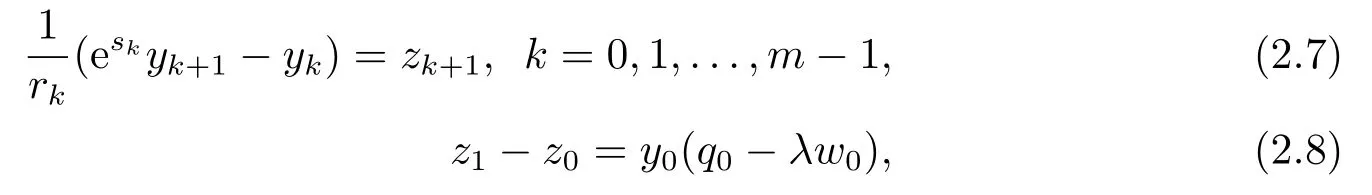

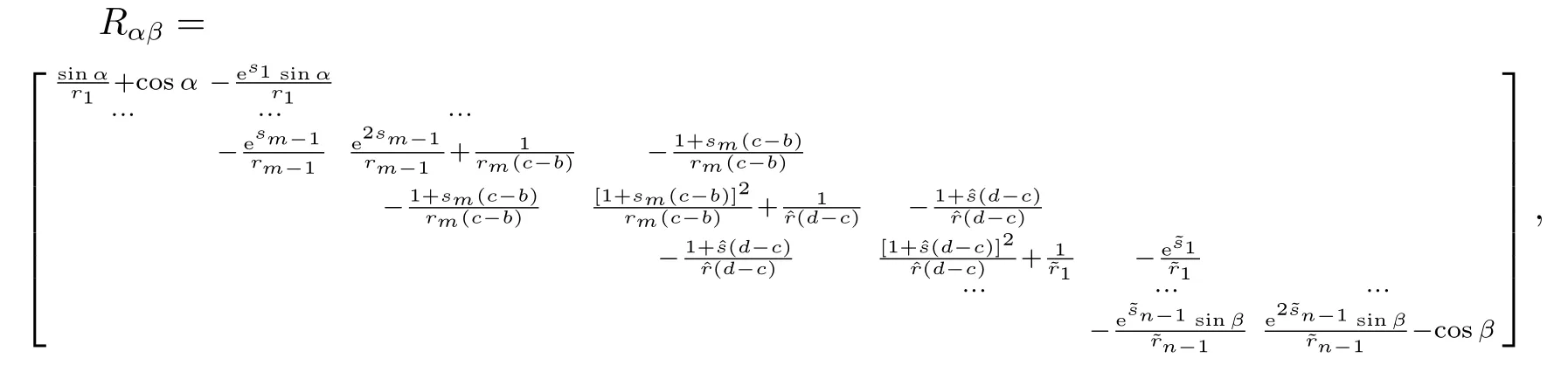


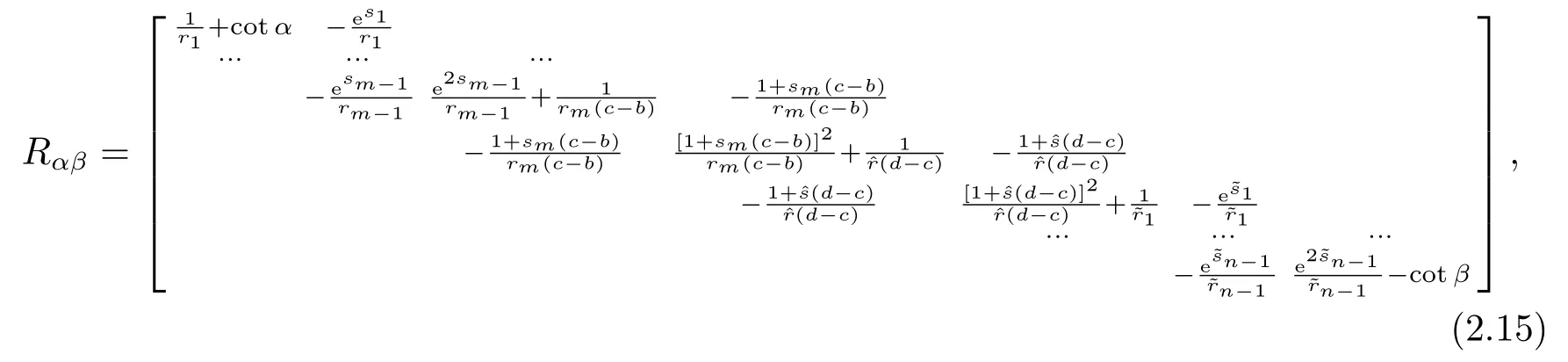
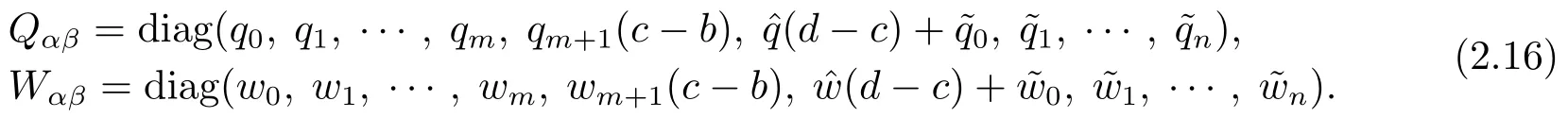

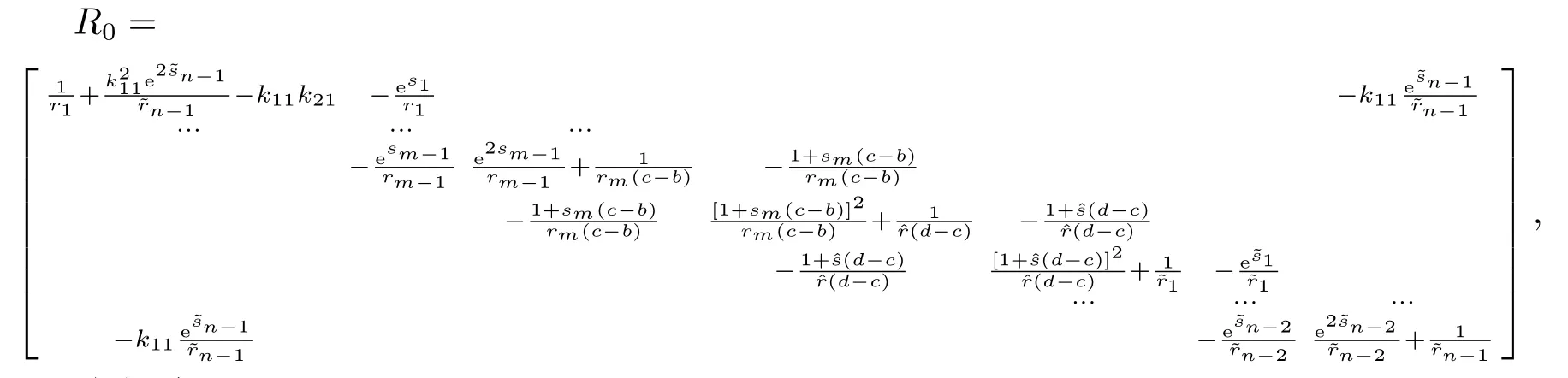
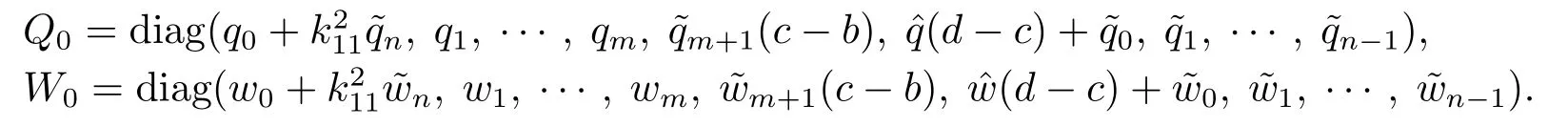

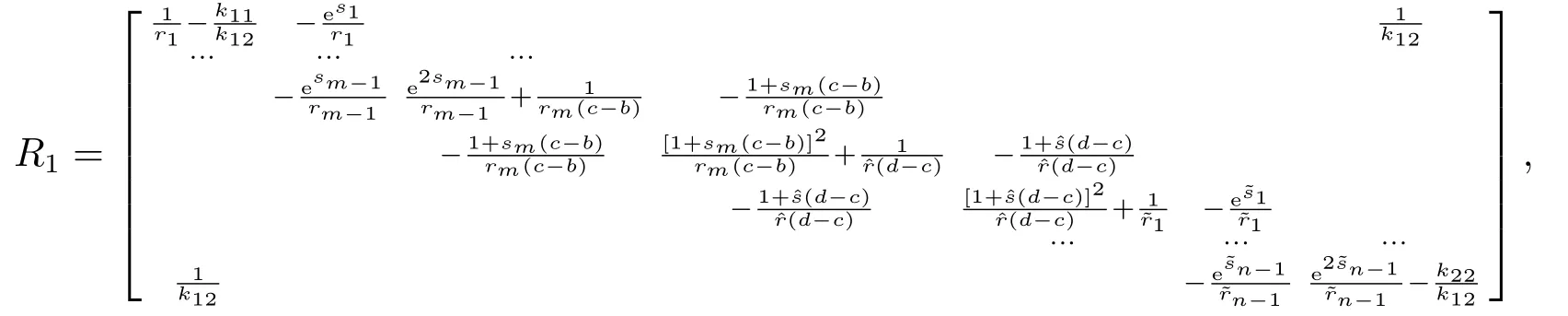
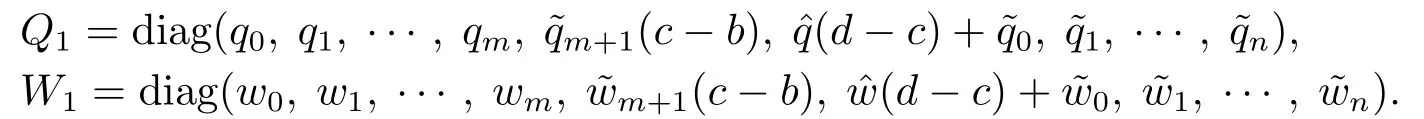


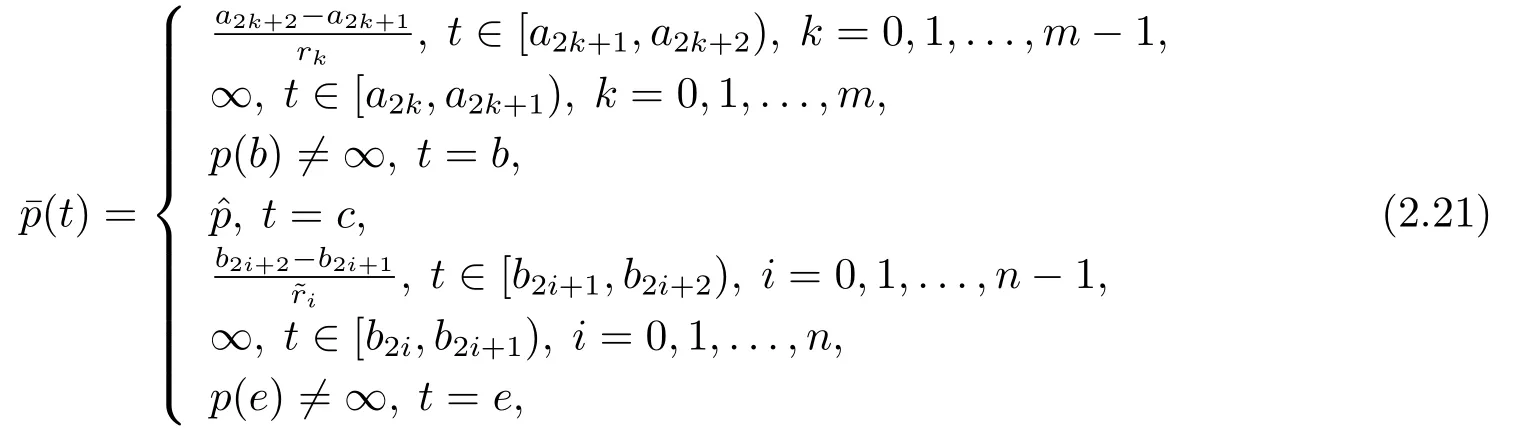
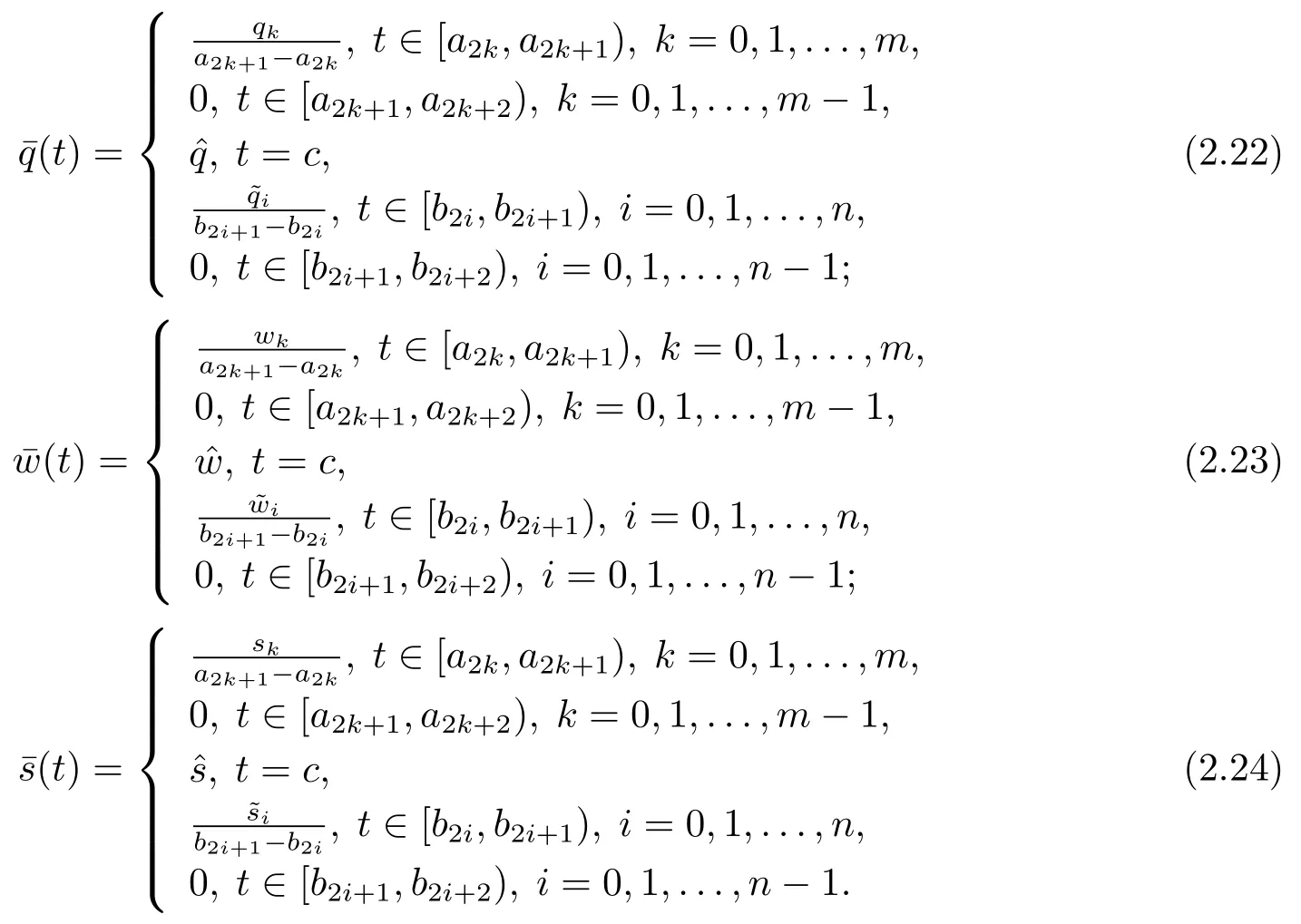

3.证明


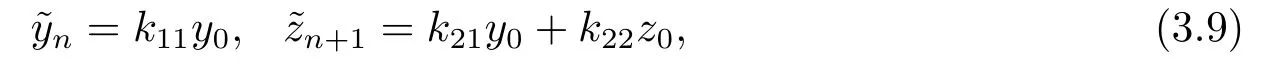


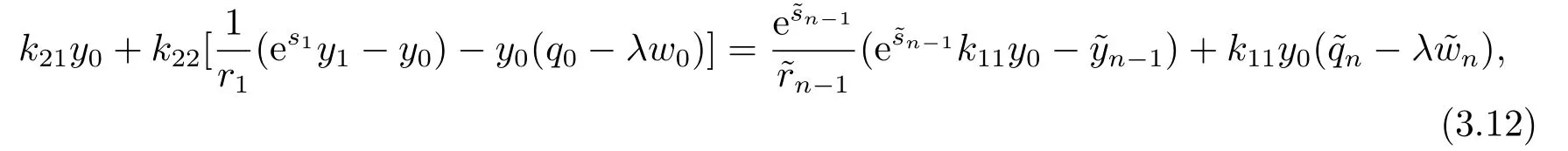

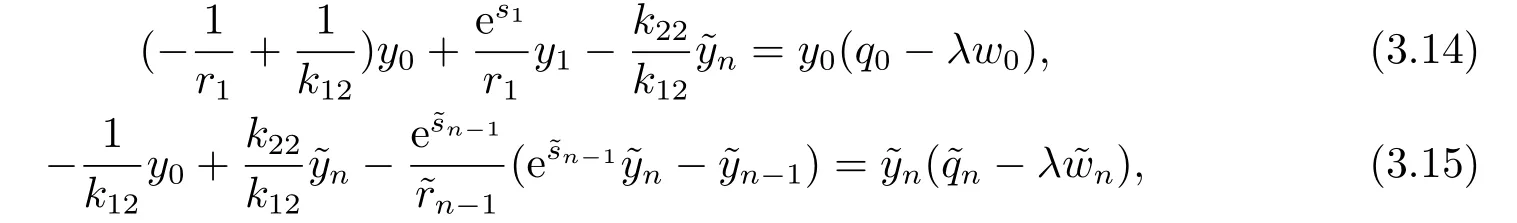
4.矩阵特征值问题的具有分布势函数的S-L问题表示