Time-Consistent Investment and Reinsurance Problems for Mean-Variance Insurers with Default Risk Under Variance Premium Principle

LI Bing(李冰),GENG Caixia(耿彩霞)

( School of Science,Hebei University of Technology,Tianjin 300401,China )

Abstract: In this paper,we consider an optimal investment-reinsurance strategy problem under mean-variance criterion for an insurer,who can trade in a risk-free asset,a stock whose price process is described by Heston model and a defaultable bond.The insurer can purchase proportional reinsurance or acquire new insurance business.In particular,we assume that the premium of insurance and reinsurance are calculated through the variance premium principle.Applying game theoretic perspective,we solve the extended Hamilton-Jacobi-Bellman (HJB) equations and derive optimal time-consistent investmentreinsurance strategies for the pre-default case and the post-default case,respectively.Finally,numerical simulations are provided to analyze the impact of model parameters on the optimal reinsurance and investment strategies.

Key words: Time-consistent strategy; Mean-variance criterion; Defaultable bond;Extended HJB equation

1.Introduction

Investment and reinsurance are two important parts of the financial market.The study of investment-reinsurance is favored by many scholars.Therefore,these problems for an insurer has been extensively studied in the literature.For example,Browne[1]studied the optimal investment problem for an insurer with the diffusion risk model to maximize the utility of terminal wealth and minimize the probability of ruin.YANG and ZHANG[2]added jump diffusion on the basis of Browne[1].XU et al.[3],LIANG et al.[4]and GUAN et al.[5]investigated optimal investment and reinsurance strategies in different situations.Furthermore,BI and GUO[6]studied an optimal investment problem for an insurer in a jump diffusion financial market under the mean-variance criterion and HUANG et al.[7]studied the optimal control problem for an insurer with constrained control variables.

To the best of our knowledge,many literatures are based on expected value premium principle.This principle is embodied in two risks with the same mean,and the same premium will be charged.But everyone agrees that the underlying danger may appear strongly different.Thus,one could therefore opt for the variance premium principle.SUN et al.[8]investigated the robust optimal investment and reinsurance of an insurer under variance premium principle.In this paper,both the insurance and reinsurance premium payments are calculated by using the variance premium principle which is more suitable for our case.

Although optimal investment-reinsurance problem has been extensively studied,most previous works assumed that the insurers are allowed to invest in one risk-free asset and one stock.The default risk is rarely considered in the modeling framework.Bielecki and Jang[9]investigated the optimal investment for an investor who can invest in a risk-free asset,a stock and a defaultable bond.Capponi and Figueroa-L´opez[10]studied a portfolio optimization problem with a defaultable bond in a regime-switching market.BO et al.[11]considered optimal investment-consumption strategy when the object function is HARA utility function in a defaultable market.ZHAO et al.[12]studied the optimal time-consistent investmentreinsurance strategy for mean-variance insurers with a defaultable security in a jump-diffusion risk model.

In most of the literature mentioned above,the price processes of risky assets are assumed to follow geometric Brownian motion,which implies that the volatilities of the risky assets’prices are constant or deterministic.Stochastic volatility is an important feature in the asset model and many empirical evidences tend to support that the volatilities of the risky assets’ prices are stochastic.WANG et al.[13]studied investment strategies for an insurer and a reinsurer under the CEV model.SUN and GUO[14]studied optimal mean-variance investment and reinsurance problem for an insurer with stochastic volatility.GU et al.[15]and A and LI[16]studied the reinsurance and investment under stochastic volatility model.

In recent years,optimal reinsurance and investment problems under the mean-variance criterion have drawn much attention.We know that dynamic mean-variance optimization problem is a time-inconsistent problem and it can not be solved by Bellman optimality principle.One approach is to study the corresponding precommitment problem,while the other is to formulate the problem in a game theoretic framework.CHEN and Yam[17]investigated an optimal investment-reinsurance problem for insurers in the market with regime-switching under the mean-variance criterion.SHEN and ZENG[18]investigated an optimal investmentreinsurance mean-variance problem for mean-variance insurers with square-root factor process.ZENG and LI[19]and ZENG et al.[20]derived the time-consistent investment and reinsurance strategies for mean-variance insurers.ZENG et al.[21]derived the robust equilibrium investment and reinsurance strategies for mean-variance insurers.

In this paper,we consider the optimal investment-reinsurance problem for mean-variance insurer in a defaultable market.The insurer’s surplus process is described by a general jump process and both the insurance and reinsurance premium are assumed to be calculated via the variance premium principle.The insurer is allowed to invest in a risk-free asset,a stock and a defaultable bond.We formulate the problem in a game theoretic framework to deal with time inconsistency.By using stochastic control theory,we solve the extented HJB equations and derive optimal investment and reinsurance strategies for the pre-default case and the post-default case,respectively.

The outline of this paper is as follows.In Section 2,we describe the model dynamics of the surplus process and the financial market.In Section 3,we propose optimal control problem under mean-variance criterion.In Section 4,we derive the closed-form expressions of the optimal investment-reinsurance strategy and the value function for the pre-default case and the post-default case,respectively.In Section 5,we present some numerical illustrations and sensitivity analysis for our results.Section 6 concludes the paper.

2.The Model

We consider a complete probability space (Ω,F,P).Let F :={Ft}t≥0be the rightcontinuous,P-complete filtration generated by two standard Brownian motions{W1(t)}and{W2(t)}.Denote H:={Ht}t≥0as the filtration of a default process{H(t)}.G:={Gt}t≥0is the enlarged filtration of F and H,i.e.,Gt:=Ft∨Ht.LetPbe the real world probability measure.We assume that there exists a risk neutral measureQequivalent to measureP.All stochastic processes introduced below are assumed to be well defined and adapted processes in this space.

We suppose that the risk process of the insurer is described by the Cramr-Lundberg(C-L) model,i.e.,

wherecis the premium rate,represents the aggregate claims up to timet,{N(t),t ≥0}is a homogeneous Poisson process with intensityλ,and{Yi,i ≥1}is a sequence of positive independent and identically distributed random variables with common distributionF(y)and finite first and second momentsµ1andµ2respectively.Assume that the premium ratecis calculated according to the variance principle,that is,whereη >0 is the relative safety loading of the insurer,E[·] denotes the expectation and Var[·] denotes the variance.

As an effective tool of reduce risk,we allow the insurer to purchase proportional reinsurance or acquire new business with the retention levelq(t)∈[0,∞) at timet.That is,for a claimYioccurring at timet,the insurer paysq(t)Yi,and the reinsurer or new businessmen pays the outstanding amount (1−q(t))Yi.For this reinsurance or new business,the premium has to be paid at the rate ofwhereθ ≥ηrepresents the relative safety loading of the reinsurer or new businessmen.

Then the surplus process of the insurer is

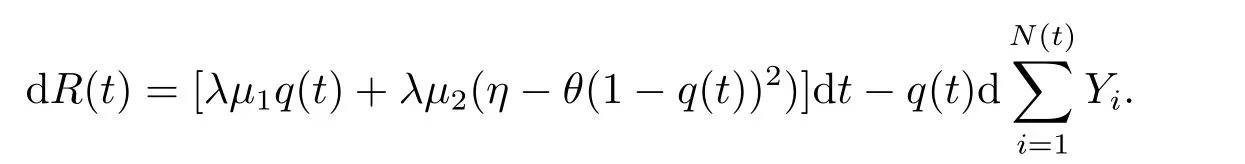
We assume that there are three assets available for an insurer in the financial market:one risk-free asset,one stock and one defaultable bond.The price process of the risk-free asset is modeled by

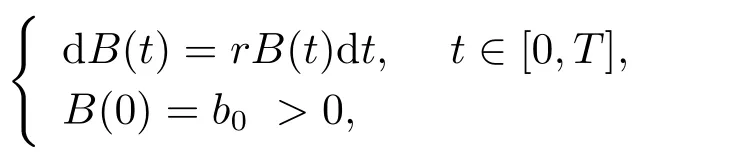
wherer >0 is the interest rate of the risk-free asset.The price process of the stock is given by the Heston model

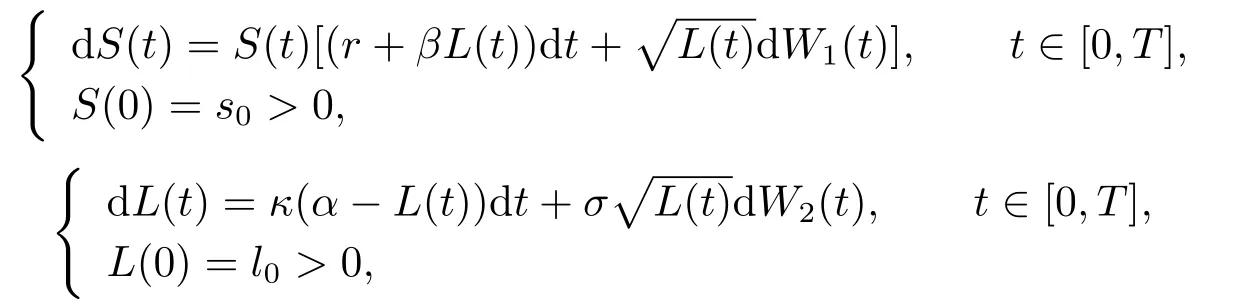
whereβ,κ,αandσare positive constants,κis the mean reversion rate,αis the long-run mean,andσis the volatility of the volatility.{W1(t)}and{W2(t)}are two one-dimensional standard Brownian motions with Cov(W1(t),W2(t))=ρt,whereρ ∈[−1,1].Moreover,we assume that 2κα ≥σ2is required to ensure that zero is not accessible orL(t)is almost surely nonnegative.

Letτbe a nonnegative random variable and the first jump time of a Poisson process defined on (Ω,F,P),representing the default time.For eacht ≥0,the default process{H(t)}is defined byH(t):=I{τ≤t}.Furthermore,we assume that the default process{H(t)}has a constant intensityhP>0.Then the process{MP(t)}is given by the following equation

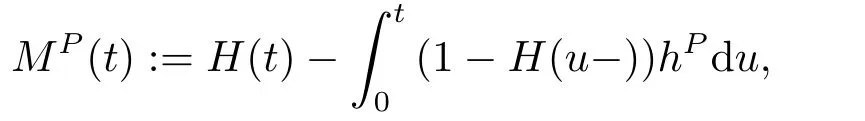
which is a (G,P)-martingale.

Letζ ∈(0,1) denote the loss rate and 1/∆≥1 denote the default risk premium.The dynamics of the defautable bond price underPfollows from

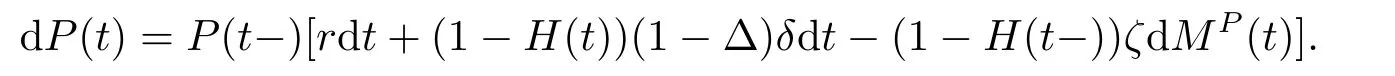
The dynamics of the defautable bond price is derived in Appendix.

LetXπ(t)denote the insurer’s wealth at timet,andπ1(t)andπ2(t)be the dollar amounts invested in the stock and the defaultable bond,respectively.A trading strategy is denoted byπ=(q(t),π1(t),π2(t))t∈[0,T].Under strategyπ,the investor’s wealth process{Xπ(t)}t∈[0,T]follows from

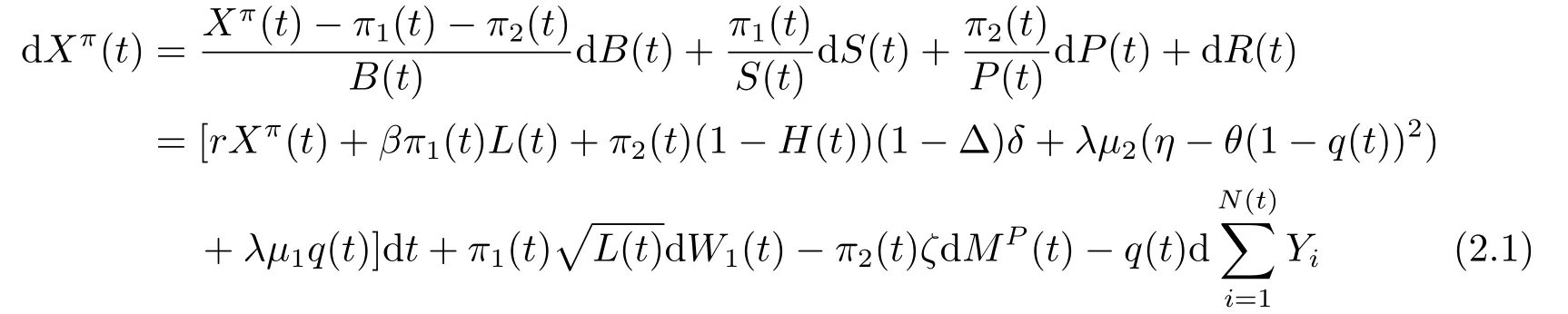
withXπ(0)=x0,(1−H(t−))dMP(t)=dMP(t) and under the convention that 0/0=0.This convention is needed to deal with the post-default case,i.e.,τ ≤t,so thatP(t)=0 and we fixπ2(t)=0 afterwards.

Definition 2.1A trading strategyπ=(q(u),π1(u),π2(u))u∈[t,T]is said to be admissible if it satisfies

1) (q(u),π1(u),π2(u)) isFu-predictable;

2)q(u)≥0,for anyu ∈[t,T];

3) (π,Xπ) is the unique strong solution to the stochastic differential equation (2.1).

For any initial condition (t,x,l,z)∈[0,T]×R×R+×{0,1},letΠ(t,x,l,z) denote the set of all admissible strategies.Herezdenotes the initial default state withz=0 andz=1 corresponding to the pre-default case (τ >t) and the post-default case (τ ≤t),respectively.

3.Problem Formulation and Verification Theorem

In this section,we will formulate the problem within a game theoretic framework,which is developed by Bjrk and Murgoci[22].We consider an optimization problem for the insurer purchasing reinsurance or acquiring new business and investing in the risk-free asset,the stock and the defaultable bond under the mean-variance criterion.At any timet ∈[0,T],the insurer aims to maximize the expectation and minimize the variance.i.e.,

In what follows,we provide the definition of the equilibrium strategy and the equilibrium value function for the problem (3.1).

Definition 3.1For any fixed initial state (t,x,l,z)∈[0,T]×R×R+×{0,1},consider an admissible strategyπ∗(t,x,l,z).Choose four fixed numbersandϵ ∈R+and define the following strategy:

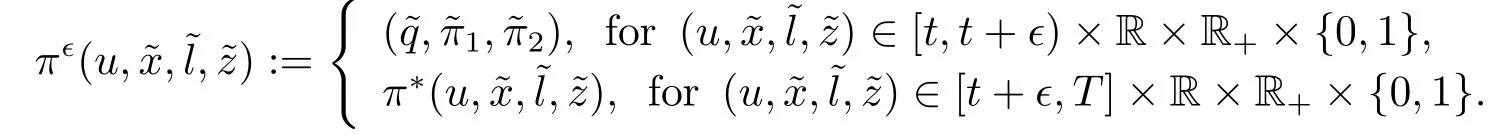
If

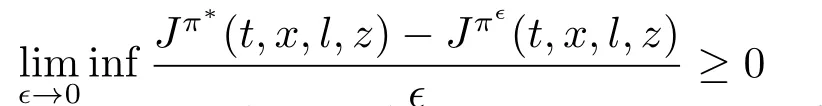
Based on the definition above,equilibrium strategy is time-consistent.Therefore,the aim of the insurer is to find an equilibrium strategy and the corresponding equilibrium value function of the optimization problem (3.1).

LetC1,2,2([0,T]×R×R+) denote the space ofϕ(t,x,l) and its derivativesϕt(t,x,l),ϕx(t,x,l),ϕxx(t,x,l),ϕl(t,x,l) andϕll(t,x,l) are continuous on [0,T]×R×R+.For anyϕ(t,x,l,0),ϕ(t,x,l,1)∈C1,2,2([0,T]×R×R+) andπ ∈Π,define the infinitesimal generator Then we have the following verification theorem.

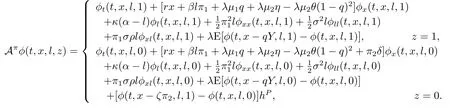
Theorem 3.1For the post-default case (z=1) and pre-default case (z=0),if there exist two real-valued functionsV(t,x,l,z),g(t,x,l,z)∈C1,2,2([0,T]×R×R+×{0,1})satisfying the following extended HJB system of equations:∀(t,x,l,z)∈[0,T]×R×R+×{0,1},

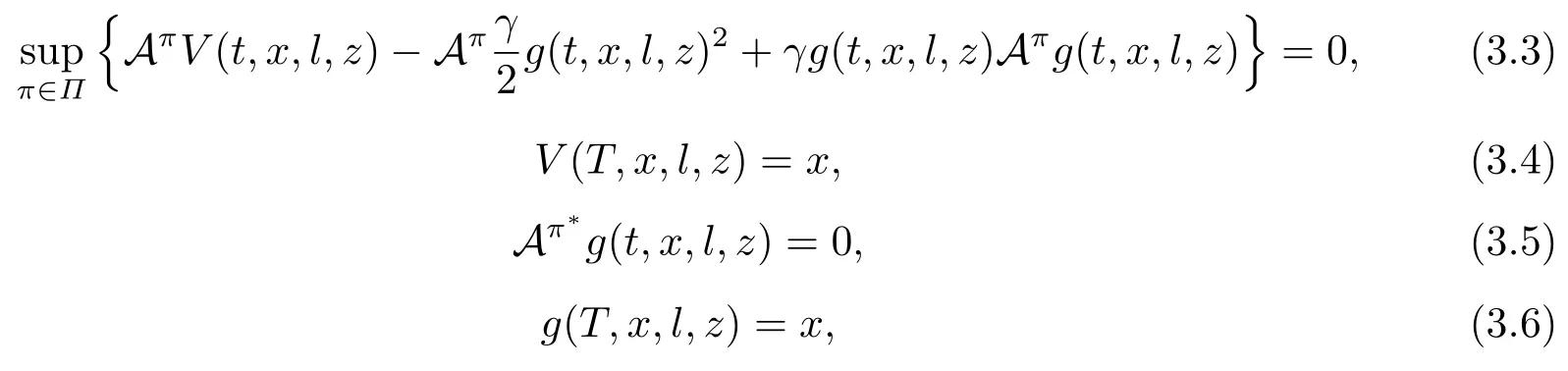
and

thenW(t,x,l,z)=V(t,x,l,z),Et,x,l,z[Xπ∗(T)]=g(t,x,l,z) andπ∗is the optimal timeconsistent strategy.

The proof of this theorem is similar to the one of Theorem 4.1 in [22],and we omit it here.

4.Optimal Investment and Reinsurance Strategy

In this section,we derive the optimal strategies and the corresponding value functions in the post-default case (z=1) and the pre-default case (z=0),respectively.

ⅠPost-default case:z=1

In the post-default case,we haveP(t)=0,τ ≤t ≤T.Thusπ2(t)=0 forτ ≤t ≤T.Letz=1 in (3.3).The HJB equation turns into a relatively form,which is the following partial differential equation

with the boundary conditions (3.4) and (3.6).Let

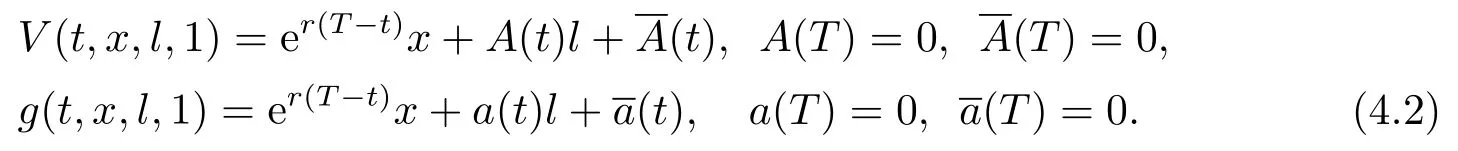
Substituting (4.2) into (4.1),we obtain

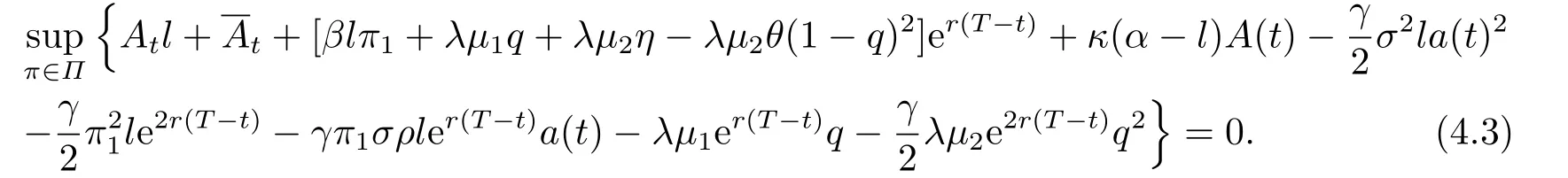
Differentiating (4.3) w.r.t.π1andqgives

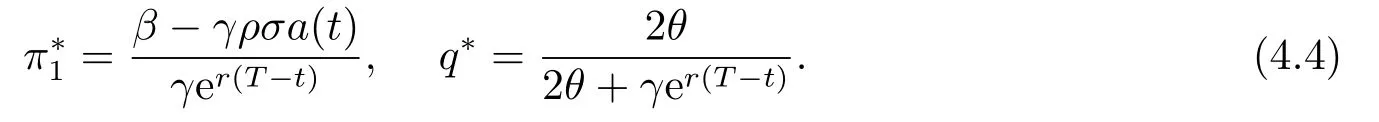
Substituting (4.4) into (4.3) and (3.5) yields

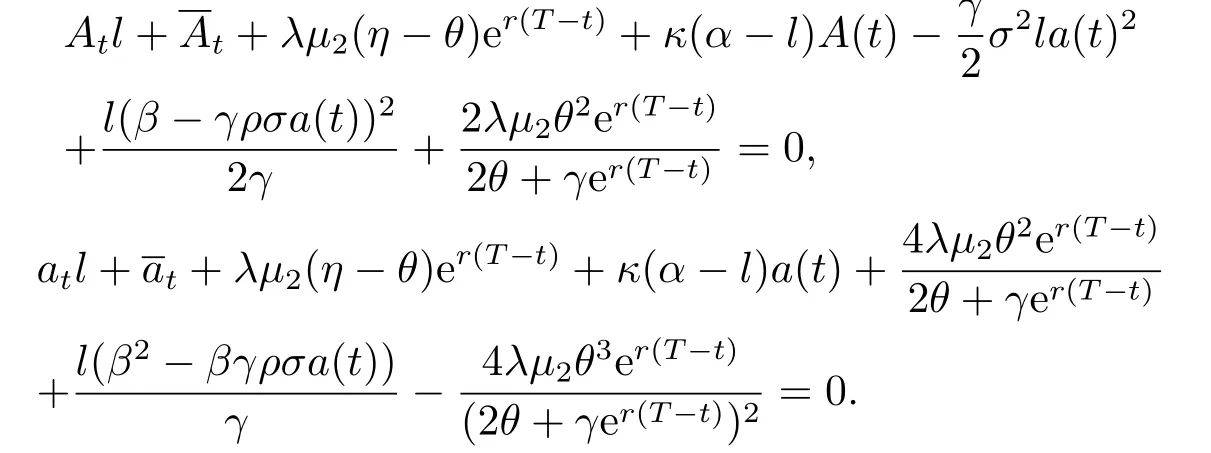
By separation of variances,we obtain four differential equations.Considering the boundary conditions,we derive

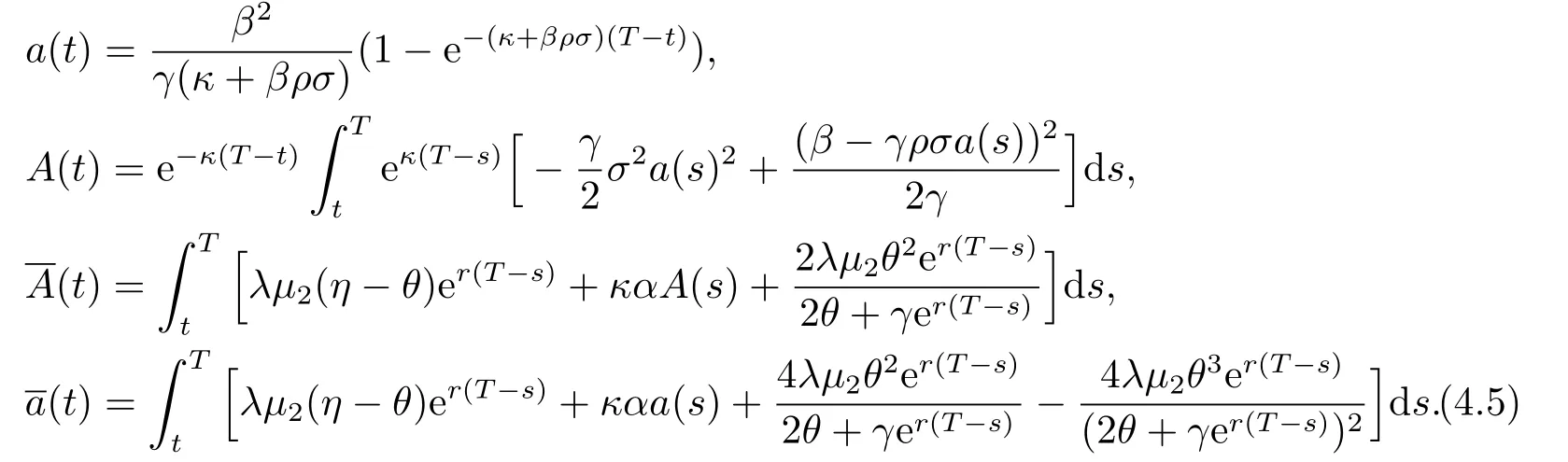
ⅡPre-default case:z=0

In the pre-default case,there exist the price process of the defaultable bond.Letz=0 in(3.3).The HJB equation turns into a relatively form which is the following partial differential equation

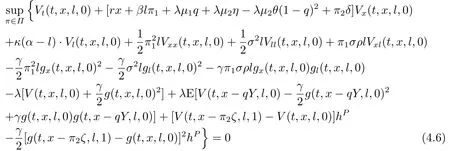
with the boundary conditions (3.4) and (3.6).Similar to the post-default case,let

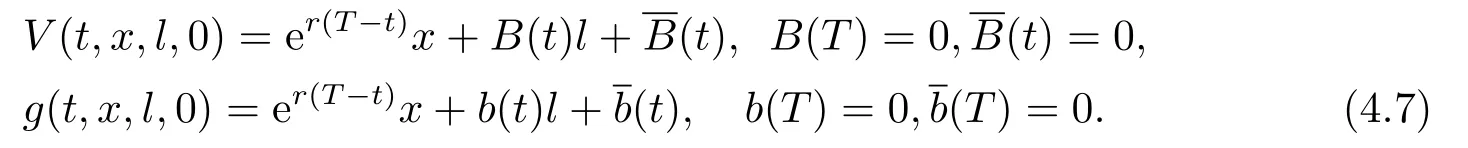
Substituting (4.7) into (4.6),we yield the following first-order condition for the maximum point (q∗,π∗1,π∗2)

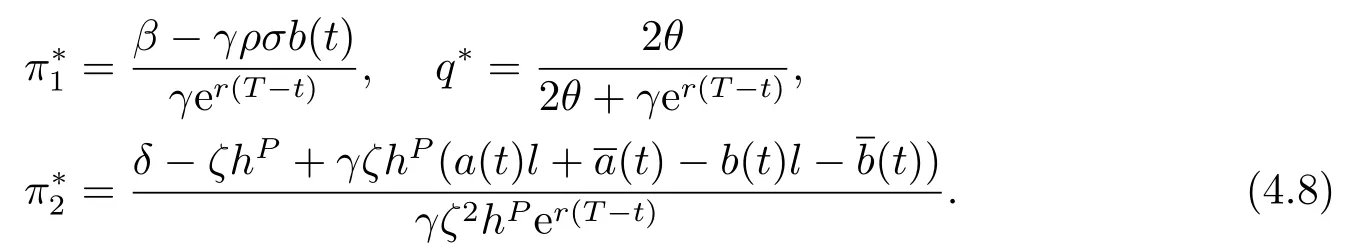
Introducing equations (4.7) and (4.8) into the equations (4.6) and (3.5) yields

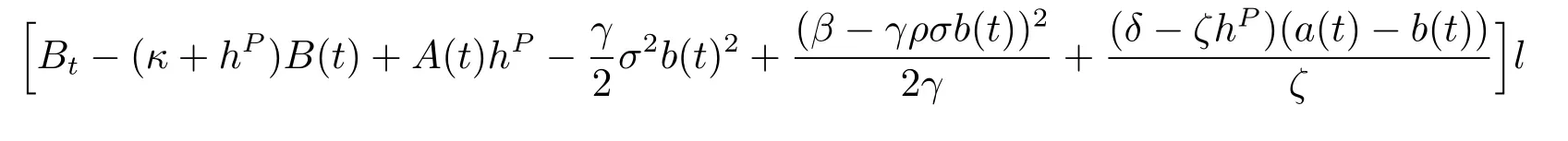
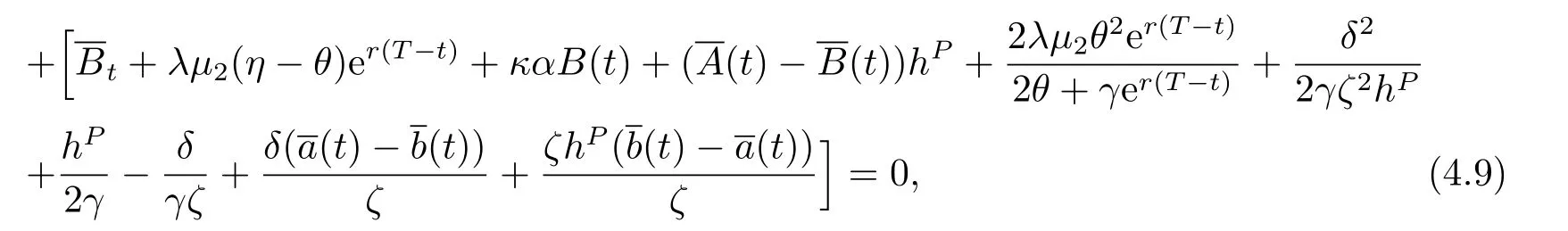
and

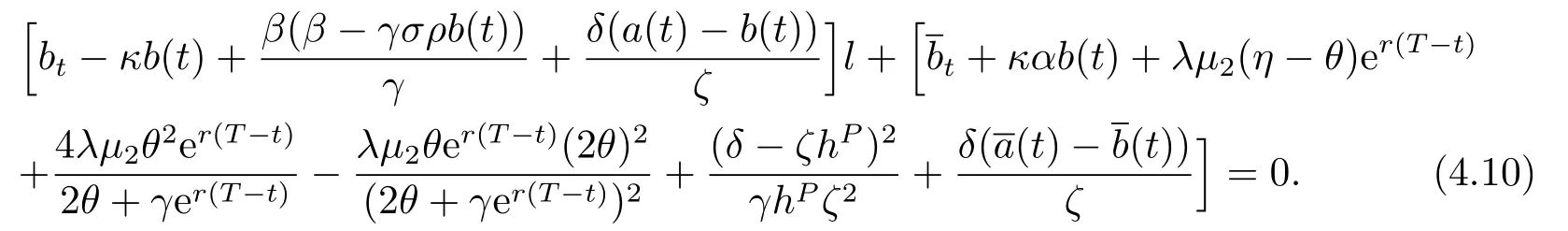
By separation of variances,we obtain four differential equations.Considering the boundary conditions,we derive

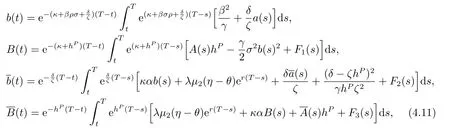
where

Theorem 4.1For the mean-variance problem(3.1),the optimal investment-reinsurance strategy is given by

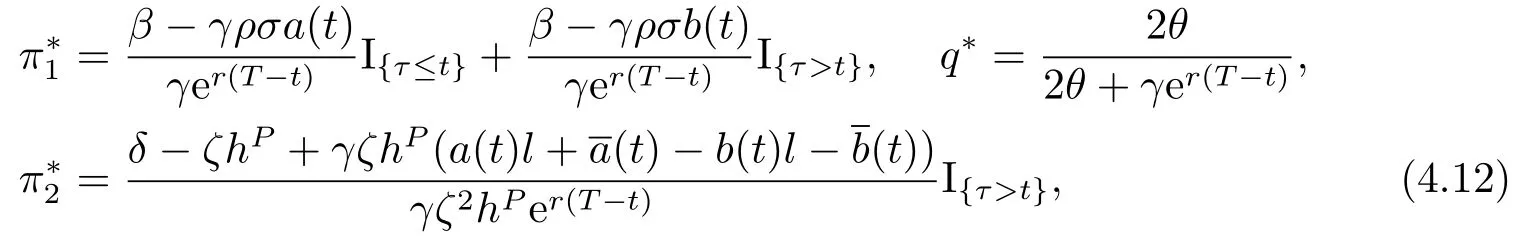
and the value functions are given by

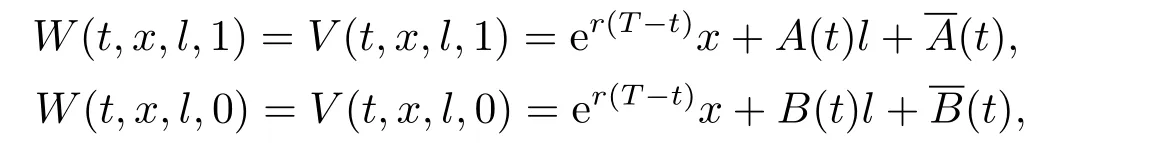
for the post-default and pre-default cases,respectively,whereA(t)A(t)B(t) andB(t) are given by (4.5) and (4.11).

5.Numerical Illustration and Sensitivity Analysis

In this section,we provide some numerical examples to illustrate the effects of model parameters on the optimal reinsurance-investment strategy.For convenience,in the following analysis,unless otherwise stated,the basic parameters are listed as follows:θ=0.4,η=0.2,β=0.3,κ=0.3,α=0.2,ρ=0.5,λ=1,µ1=0.3,µ2=0.5,r=0.04,γ=1,σ=0.2,T=10,t=0,x=1,δ=0.02,ρ=0.5,ζ=0.2 andhP=0.005.We give the detailed analysis for the optimal investment-reinsurance strategyπ∗1(t),π∗2(t) andq∗(t).

Fig.1 and Fig.2 show that the optimal reinsurance strategyq∗(t)increases with respect to timet,namely,as time elapses,the insurer should keep more insurance business by purchasing less reinsurance or acquire more new business.In addition,Fig.1 illustrates that when the safety loading of the reinsurerθincreases,the insurer will purchase less reinsurance or acquire more new business.Fig.2 illustrates that the optimal reinsurance strategy decreases w.r.t.the absolute risk aversion parameterγ,the insurer will purchase more reinsurance or acquire less new business.

Fig.1 The first subfigure

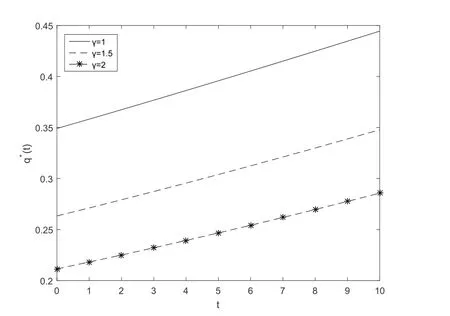
Fig.2 The second subfigure

Fig.3 and Fig.4 show that the optimal investment strategyπ∗1(t)increases with respect to timetfor the post-default case.Fig.3 illustrates that the optimal investment strategyπ∗1(t)decreases when the absolute risk aversion parameterγincreases.In other words,the largerγis,the more risk averse the insurer is.Fig.4 illustrates that the optimal investment strategyπ∗1(t) decreases when correlation coefficientρincreases.

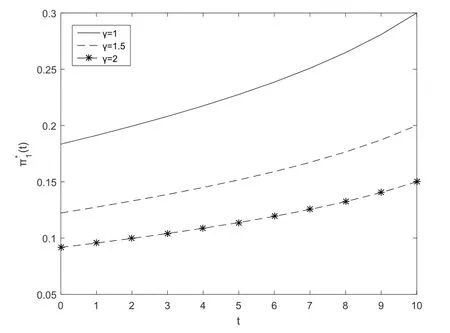
Fig.3 The first subfigure

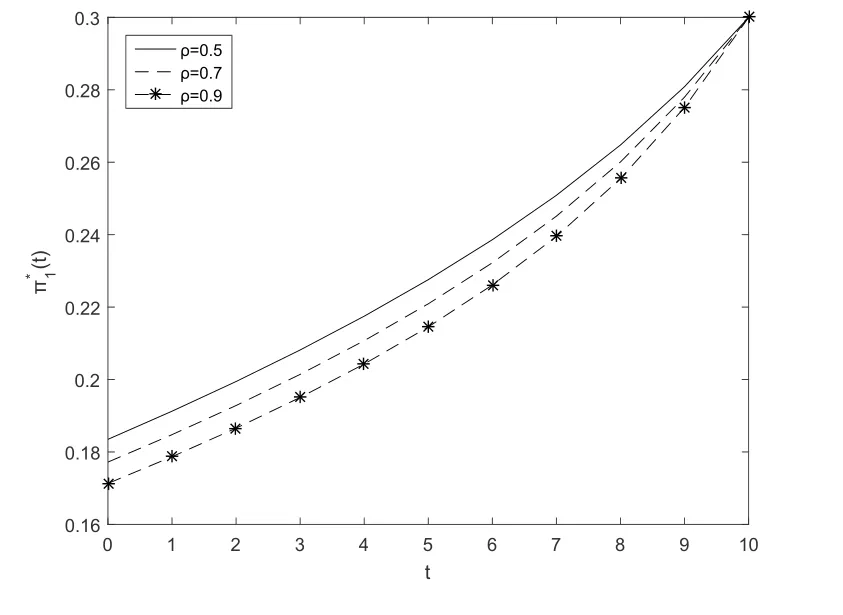
Fig.4 The second subfigure

Fig.5 and Fig.6 show that the optimal investment strategyπ∗1(t) decreases with respect totfor the pre-default case.Fig.5 illustrates that the optimal investment strategyπ∗1(t)decreases whenδincreases.Fig.6 illustrates that the optimal investment strategyπ∗1(t) decreases whenγincreases,which means that the insurer is averse to risk.Fig.7 and Fig.8 show that the optimal investment strategyπ∗2(t) decreases with respect toγ.Fig.7 illustrates that the optimal investment strategyπ∗2(t) decreases whenγincreases.Fig.8 illustrates that the optimal investment strategyπ∗2(t) increases whenδincreases.

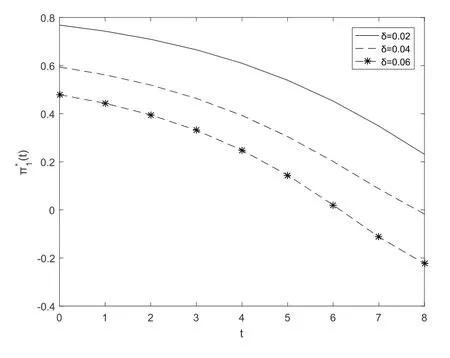
Fig.5 The first subfigure

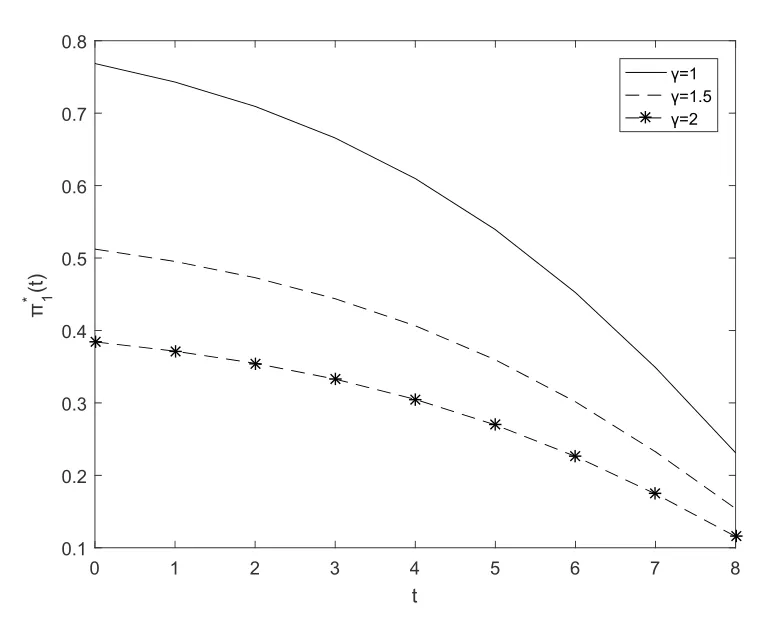
Fig.6 The second subfigure

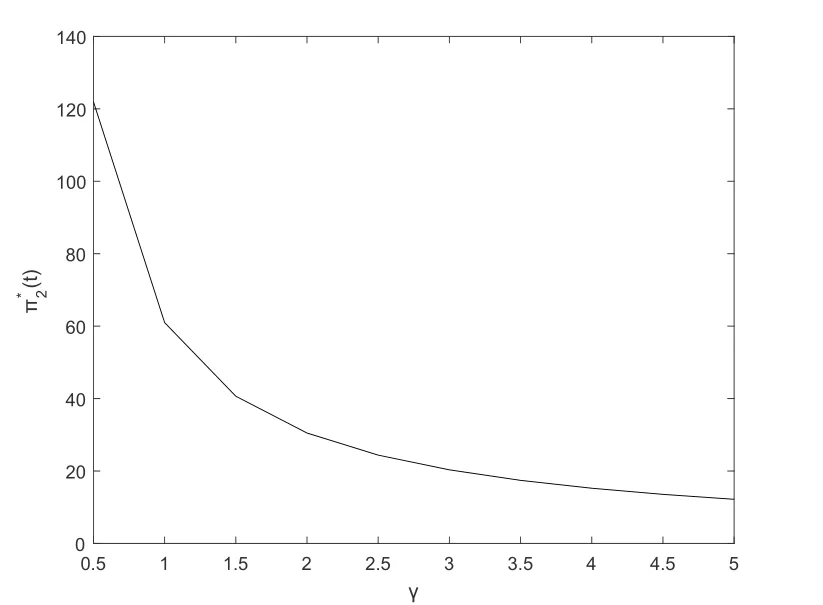
Fig.7 The first subfigure

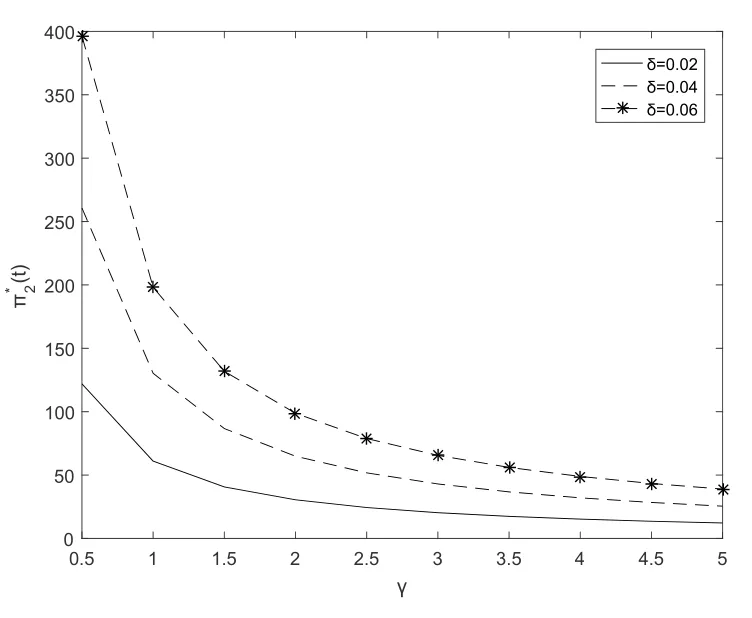
Fig.8 The second subfigure

6.Conclusion

In this paper,we investigate the optimal time-consistent investment-reinsurance problem for mean-variance insurer in a defaultable market.The insurer’s surplus process is described by a general jump process and both the insurance and reinsurance premium are assumed to be calculated via the variance premium principle.The insurer is allowed to invest in a risk-free asset,a stock and a defaultable bond.By using stochastic control theory,we solve the extented HJB equations and derive optimal investment and reinsurance strategies for the pre-default case and the post-default case,respectively.Finally,we also give a numerical example and some figures to illustrate our results.We find that: 1) the default event has no effect on the optimal reinsurance strategy; 2) the default event has an impact on the optimal dollar amount invested in the stock due to the stock price follows Heston model.In future research,we can consider more complicated models,such as the mean-variance criterion with state-dependent risk aversion or the stochastic default intensity.These problems may be more complicated calculation.

Appendix

In this appendix we derive the price for a defaultable bond.LetQbe the risk-neutral probability measure.Denote 1/∆≥1 as the default risk premium,1−ζas the default recovery rate,ζ ∈(0,1) as the loss rate,andhQ=hP/∆as the default intensity under the risk-neutral measureQ.

The pre-default value of the bond at timetis given by

Differentiating (7.1) with respect totyields

By some standard calculus

We now define the price process for a defaultable bond underQas follows

Recall thatH(t)=I{τ≤t},and note that dH(t)=(1−H(t))dH(t),V(t)dH(t)=V(τ)dH(t)and er(t−τ)dH(t)=dH(t).Applying Itˆo’s formula to (7.4),we obtain

Moreover,the price of{P(t)}t≥0under the physical probability measurePis