一类具有内部存储的非均匀恒化器模型的共存解
李星星,聂华
( 陕西师范大学数学与信息科学学院,陕西 西安710119)
1.引言
恒化器是用于微生物连续培养的一种实验装置,经典的恒化器模型假设微生物对养料的吸收率与自身生长率成比例,这种模型被称为常数产量模型(见文[1]).Ketchum[2]实验观测发现当外部养料耗尽后,细菌仍可继续生长和分裂一段时间,直到内部储备耗尽.这表明物种的生长不仅与外部营养有关,还依赖于体内储存的营养.为描述该现象,Droop[3]提出了带有内部存储的浮游植物生长模型,这种模型被称为可变产量模型或Droop模型.Grover[4]研究了多物种竞争单资源的Droop模型,通过数据模拟分析不同参数对物种竞争结果的影响.Lange和Oyarzun[5]研究了均匀搅拌的单物种Droop模型解的全局渐近稳定性.Smith和Waltman[6]建立了如下具有内部存储的两物种竞争的均匀恒化器模型:

其中S(t),u(t)和v(t)分别代表营养物的浓度以及物种u和v在t时刻的密度.Q1(t),Q2(t)分别代表t时刻物种u和v体内每个细胞所储存的营养物浓度.S(0)>0是营养物的输入浓度,D表示恒化器的稀释率.对于i=1,2,µi(Qi)是物种生长率,依赖于细胞配额Qi;fi(S,Qi)为营养的吸收率,依赖于营养的浓度S和细胞配额Qi.Qmin,i表示细胞配额的临界值,若低于此数值物种将停止生长.
文[6]借助于单调动力系统理论建立了系统(1.1)的竞争排斥原理.Hsu等[7]研究了具有内部存储的多物种竞争的均匀恒化器模型,结果表明均匀搅拌情形下,多物种竞争的Droop模型仍有竞争排斥原理成立.为解释实验和现实生态系统中的共存现象,Hsu等[8−9]引入扩散,建立了具有扩散的两物种竞争的Droop模型.他们令U=Q1u,V=Q2v,则U,V分别表示两物种储存的总营养.因此具有扩散的两物种竞争的Droop模型(即具有内部存储的非均匀恒化器模型)为:

其中d和γ分别为扩散系数和产出率.初始函数u0(x),U0(x),v0(x),V0(x)满足关于模型更详细的生物背景及建模机理见文[3–5,8].
文[8-9]采用单调动力系统理论及系统平衡解关于扩散系数的单调性,建立了单物种模型存活与消亡的临界扩散系数,其研究结果表明存在临界的扩散系数d0使得当0< d < d0时,单物种存活; 当d ≥d0时,单物种消亡.因此对于两物种竞争的模型(1.2),存在正数d0,1和d0,2,使得当0 其中Qc,1≥Qmin,1,Qc,2≥Qmin,2,满足µ1(Qc,1)=µ2(Qc,2)=η0,η0是如下问题的主特征值: 文[8]采用单调动力系统理论研究了系统(1.2)的共存解,结果表明当时,两竞争物种可以共存.文[9]进一步利用系统(1.2)的单调性及半平凡解的稳定性分析,拓展了文[8]的结果,即当时,系统(1.2)也存在共存解.总结文[8-9]结果可得如下定理: 定理1.1[8−9]当0 HSU,LAM和WANG[10]考虑了一类带有内部存储的单物种消耗无机碳的反应扩散模型,证明临界存活/消亡扩散系数可由一类非线性特征值问题的主特征值刻画.受该工作的启发,本文主要借助锥上的不动点指标理论和非线性特征值问题研究系统(1.2)正平衡解的存在性.研究的主要困难来源于系统(1.2)中比率项分别在(u,U)=(0,0)和(v,V)=(0,0)的奇性.因此通常的线性化方法、分歧理论以及拓扑不动点指标理论等均不适用.特别地,在使用锥上的拓扑不动点指标理论研究模型正平衡解的存在性时,通常选取Banach空间自然的正锥,而且非线性算子不动点指标的计算一般借助于相应的线性化算子的谱分析来给出(见[11]).然而本模型在(u,U)=(0,0)和(v,V)=(0,0)的奇性,使得通常借助于线性算子谱分析来计算非线性算子不动点指标的方法也不适用.本文为克服比率项分别在(u,U)=(0,0)和(v,V)=(0,0)的奇性,首先建立了模型正平衡解更细致的先验估计,从而能在正锥的内部选取一个特殊的锥来研究模型正平衡解的存在性.然后利用该特殊锥上的不动点指标理论,直接借助于非线性特征值问题的主特征值计算非线性算子在平凡解、半平凡解处的不动点指标,从而建立模型正平衡解的存在性. 为此,根据文[3]的具体实例,对反应函数µi(Qi)和fi(S,Qi)(i=1,2)作如下假设: (H1)µi(Qi)在[Qmin,i,∞)上连续可微,且µi(Qmin,i)=0.当Qi≥Qmin,i时,µ′i(Qi)>0. (ii) 存在QBi∈(Qmin,i,+∞] 使得在[0,∞)×[Qmin,i,QBi) 上有且当S=0或者Qi≥QBi时fi(S,Qi)=0 (若QBi=∞,则fi(S,Qi)=0当且仅当S=0). 本文主要研究(1.2)正平衡解存在性,因此只需考虑(1.3)对应的平衡态问题 由于我们仅关注模型(1.4)的非负解,因此可对反应函数fi(S,Qi)和µi(Qi)(i=1,2)作如下延拓: 易得Fi(S,Qi)在R×R上Lipschitz连续以及(Qi)在R上Lipschitz连续.为方便,仍分别记Fi(S,Qi),(Qi)为fi(S,Qi),µi(Qi). 记Q∗i=inf{Qi>0:fi(z(x),Qi)−µi(Qi)Qi≤0,x ∈[0,1]},i=1,2,E=C0([0,1],R2+)以及 则E,W1,W2为C0([0,1],R2)的完全锥,且E是实的正规锥.定义(u1,v1)≫E(u2,v2)当且仅当(u1,v1)−(u2,v2)∈intE. 考虑非线性特征值问题 由文[10]的引理5.1可知(2.1)存在主特征值,记为λ0i,相应的正特征函数(ϕi,φi)∈Wi,且(ϕi,φi)≫E(0,0).根据[10]的引理7.1可得如下结果: 引理2.1[10]对任意的d>0,令λ0i:=λ0i(d)(i=1,2)是特征值问题(2.1)的主特征值,则存在d0,i>0,有如下结果成立: (i) 若0 (ii) 若d=d0,i,则λ0i(d)=0; (iii) 若d>d0,i,则λ0i(d)<0. 注2.1由临界扩散系数d0,1,d0,2的唯一性知,此处的临界扩散系数d0,1,d0,2与文[9]中得的临界扩散系数相同. 考虑单物种模型 引理2.2[10]若d ≥d0,1,则(u,U)=(0,0)是(2.2)的唯一非负解; 若0 注2.2对另一个具有内部存储的单物种模型 类似可得若0 下面给出(1.4)正解的先验估计. 引理2.3设(u,U,v,V)是系统(1.4)的非负解,且则 (i)u>0,U >0,v >0,V >0; (ii)U+V (iii)Qmin,1u 证(i)和(ii)证明可参考文[12]的引理2,由文[8]的引理3.3可证U > uQmin,1,V > vQmin,2,故省略.这里只给出U < Q∗1u和V < Q∗2v的证明.记显然,对于i=1,2,µi(Ai),fi(z(x)−U −V,Ai)可写成如下形式: 对于每个Qi≥Qmin,i, 根据Q∗i的定义可知fi(z(x),Q∗i)−µi(Q∗i)Q∗i≤0,i=1,2.由(i)得z −U −V < z,从而fi(z(x)−U −V,Q∗i)−µi(Q∗i)Q∗i<0,i=1,2. 令H1(x)=U(x)−Q∗1u(x),H2(x)=V(x)−Q∗2v(x),则Hi(x)满足 及如下不等式: 由极值原理可得Hi(x)<0(x ∈[0,1]),即U 本节讨论系统(1.2)正平衡解的存在性,即(1.4)正解的存在性.为此引入以下空间: 其中∥·∥为最大模范数, 定义F:Ω →X为 ξi(x;Qi)和ϑi(x;Qi)分别由(2.4)和(2.5)给出.显然F:Ω →X是紧的. 下面证明F:Ω →W.对任意(u,U,v,V)∈Ω,令则满足 由(3.1)及最大值原理,易知0000.因此只需证明为此令由(u,U,v,V)∈Ω可得G1=U −Qmin,1u ≥0.由于 则H1满足以及如下不等式: 由极值原理易得(x)≥0(x ∈[0,1]),即同理可证因此故F:Ω →W.于是,方程(1.4)有非负解等价于F在Ω内有不动点. F的所有平凡和半平凡非负不动点包括(0,0,0,0),(u∗,U∗,0,0)和(0,0,v∗,V ∗).为了使用度理论,我们需要计算F在这些非负不动点的指标. 引理3.1当λ ≥1时,F(u,U,v,V)=λ(u,U,v,V)在W中没有满足∥u∥+∥U∥+∥v∥+∥V ∥=R0的解. 证设(u,U,v,V)∈W满足F(u,U,v,V)=λ(u,U,v,V)且∥u∥+∥U∥+∥v∥+∥V ∥=R0, 则可得以下方程: 令y=z(x)−U −V,则y满足 首先证明y(1)≥0.若y(1)<0,由边界条件知yx(1)>0.存在a ∈[0,1),使得对任意的x ∈(a,1],y(x)<0,其中a=0或y(a)=0.由方程(3.2)得对任意的x ∈[a,1],yxx≤0,故yx(x)≥yx(1)>0,即y(x)在[a,1]上单调递增.由yx(0)=−S(0)<0可得0,故y(a)=0,这与y(x)在[a,1]上单调递增矛盾.因此y(1)≥0.下证b ∈[0,1),y(b)≥0,否则存在b ∈[0,1)使得y(b)<0.由连续性可得,存在δ1≥0,δ2>0,使得对任意的x ∈(b −δ1,b+δ2)⊂(0,1),y(x)<0,其中y(b+δ2)=0,b −δ1=0或y(b −δ1)=0.同样可得对任意的x ∈(b −δ1,b+δ2),yxx≤0.故yx(x)≥yx(b+δ2).根据y(b+δ2)=0易得y(x)在[b−δ1,b+δ2]上是单调不减的.由yx(0)=−S(0)<0可知b −δ10,故y(b −δ1)=0.因此可得y(x)≡0(x ∈(b −δ1,b+δ2)),与y(b)<0矛盾.综上所述y ≥0(x ∈[0,1]),即U+V ≤z(x). 由(u,U,v,V)∈W可得U ≥uQmin,1,V ≥vQmin,2.因此∥u∥+∥U∥+∥v∥+∥V ∥≤故F(u,U,v,V)=λ(u,U,v,V)在W中没有满足∥u∥+∥U∥+∥v∥+∥V ∥=R0的解. 引理3.2index(F,˙Ω,W)=1,其中˙Ω表示的是Ω相对于W的内部. 证根据引理3.1和文[13]的引理12.1(i)可证. 引理3.3设0 证对任意给定的ϵ0>0足够小,选取0< δ < δ0≪1使得记Sδ+={(u,U,v,V)∈W:∥u∥+∥U∥+∥v∥+∥V ∥=γδS(0)}.易见从而∥u∥≤δz,∥U∥≤δz,∥v∥≤δz,∥V ∥≤δz.令ψ=2+γ −γx2,则ψ >0(x ∈[0,1])且满足ψxx<0,ψx(0)=ψx(1)+γψ(1)=0.因此(ψ,Qmin,1ψ,ψ,Qmin,2ψ)∈W.下证对任意的λ ≥0,方程上无解.假设方程存在解(u,U,v,V),则(u,U,v,V)满足 由引理2.1知当0< d 令O+(u∗,U∗,0,0)和O+(0,0,v∗,V ∗)分别表示(u∗,U∗,0,0)和(0,0,v∗,V ∗)在W中的邻域.下面计算F在O+(u∗,U∗,0,0)和O+(0,0,v∗,V ∗)上的指标.为此引入特征值问题 由文[10]知(3.3)和(3.4)存在主特征值,分别记为Λ01和Λ02,其对应的主特征函数(η1,θ1)∈W1,(η2,θ2)∈W2,且满足(η1,θ1)≫E(0,0),(η2,θ2)≫E(0,0). 引理3.4设0 (i)当Λ02<0时,index(F,O+(u∗,U∗,0,0),W)=1;当Λ02>0时,index(F,O+(u∗,U∗,0,0),W)=0; (ii)当Λ01<0时,index(F,O+(0,0,v∗,V ∗),W)=1;当Λ01>0时,index(F,O+(0,0,v∗,V ∗),W)=0. 证由于(i)和(ii)的证明完全类似,这里仅给出(i)的证明.定义 则算子方程F(t)(u,U,v,V)=(u,U,v,V)等价于若(u,U,v,V)是F(t)在∂O+(u∗,U∗,0,0)上的不动点,则u>0,U >0,v ≥0,V ≥0.由最大值原理得v >0,V >0,否则(u,U,v,V)=(u∗,U∗,0,0),与(u,U,v,V)∈∂O+(u∗,U∗,0,0)矛盾. 下证对任意的t ∈[0,1],F(t)在∂O+(u∗,U∗,0,0)上没有不动点.假设(u,U,v,V)∈∂O+(u∗,U∗,0,0)是F(t)的不动点,则u>0,U >0,v >0,V >0.当t=0时,方程如下: 由引理2.2可得,当0< d 根据(3.4)易知,若Λ020,(3.7)只有零解,即(u,U,v,V)=(u∗,U∗,0,0).与(u,U,v,V)∈∂O+(u∗,U∗,0,0)矛盾.当t >0时,由(3.5)可得(u,U,tv,tV)>(0,0,0,0)是F在内的正不动点,这与假设矛盾.因此对任意的t ∈[0,1],F(t)在∂O+(u∗,U∗,0,0)上没有不动点.根据拓扑度理论的同伦不变性可得 类似可证(u∗,U∗,0,0)是F(0)在O+(u∗,U∗,0,0)上唯一的不动点.因此 对于τ ∈[0,1],定义 那么T(τ)(u,U,v,V)=(u,U,v,V)满足 类似可证T(τ)在∂O+(u∗,U∗,0,0)上没有不动点,且易得T(0)=F(0),T(1)=T1×T2,其中 根据拓扑度理论的同伦不变性和乘积定理[15]可得 下证index(T1,(u∗,U∗),W1)=1.令∥u∥+∥U∥≤δ},∂Pδ={(u,U)∈W1:∥u∥+∥U∥=δ}.当λ ≥1时,设(u,U)满足方程T1(u,U)=λ(u,U),则 类似引理3.1可证U ≤ z(x).由(u,U)∈ W1易知,故∥u∥+∥U∥< δ,即当λ ≥1时,T1(u,U)=λ(u,U)在∂Pδ上没有解.因此,根据文[13]的引理12.1(i)得index(T1,Pδ,W1)=1.取0< δ0≤min[0,1]{u∗,U∗},对任意的λ ≥0,令ρ=2+γ −γx2,设方程(u,U)−T1(u,U)=λ(ρ,Qmin,1ρ)在∂Pδ0上存在解(u,U),则 因此(u,U)是(2.2)的上解.由单调方法和(u∗,U∗)的唯一性,可得u ≥u∗,U ≥U∗,这与∥u∥+∥U∥=δ0矛盾.因此,index(T1,Pδ0,W1)=0.又因为(u,U)=(u∗,U∗)是T1在PδPδ0上唯一的不动点,有 下面计算index(T2,(0,0),W2).当Λ02<0时,对任意的λ ≥1,设(v,V)∈∂O+(0,0)且满足方程T2(v,V)=λ(v,V),则 由λ ≥1可得(v,V)满足微分不等式 根据(3.8)易得(v,V)是如下抛物问题的下解: 根据(v,V)∈∂O+(0,0)可知存在M1>0,使得(v(x),V(x))≤M1(η2,θ2).易证为(3.9)的上解.由比较原理可得 又因为Λ02<0,所以由(3.10)得(v,V)=(0,0).即当λ ≥1时,方程T2(v,V)=λ(v,V)在∂O+(0,0)上无解.因此由文[13]的引理12.1(i)可得,index(T2,(0,0),W2)=1.若Λ02>0,令ζ=2+γ −γx2,设(v,V)满足方程(v,V)−T2(v,V)=λ(ζ,Qmin,2ζ),则 由(3.11)可得(v,V)为(3.9)的上解.同理,存在ϵ>0,使得ϵ(η2,θ2)≤(v(x),V(x)).易证ϵeΛ02t(η2,θ2)为(3.9)的下解.根据比较原理可得 又因为Λ02>0,令t →∞,则(3.12)必与(v,V)∈∂O+(0,0)矛盾.即当λ ≥0时,方程(v,V)−T2(v,V)=λ(ζ,Qmin,2ζ)在∂O+(0,0)上无解.因此,根据文[13]的引理12.1(ii)可得当Λ02>0时,index(T2,(0,0),W2)=0. 综上所述, 定理3.1设0 证(反证法) 假设F在没有正不动点,则它在内仅有平凡的不动点(0,0,0,0)与半平凡的不动点(u∗,U∗,0,0),(0,0,v∗,V ∗),从而 然而由引理3.2-3.4计算(3.13)可得矛盾表达式 故F在至少存在一个正的不动点,即系统(1.2)至少存在一个正平衡解. 本文主要通过锥上的不动点理论研究系统(1.2)正平衡解的存在性.主要结果定理3.1表明系统(1.2)正平衡解的存在性与一类非线性特征值问题的主特征值符号有关.定理3.1与定理1.1均假设0< d 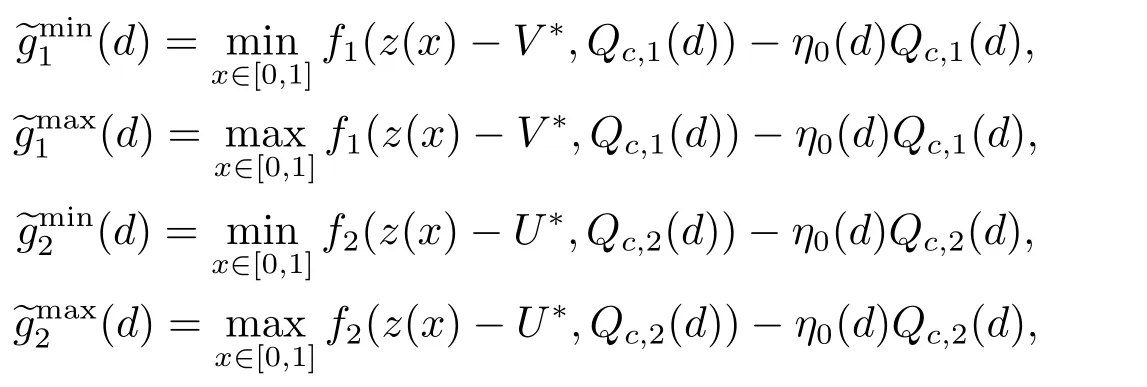



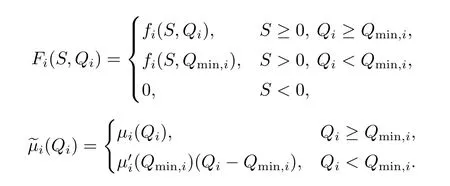
2.准备知识


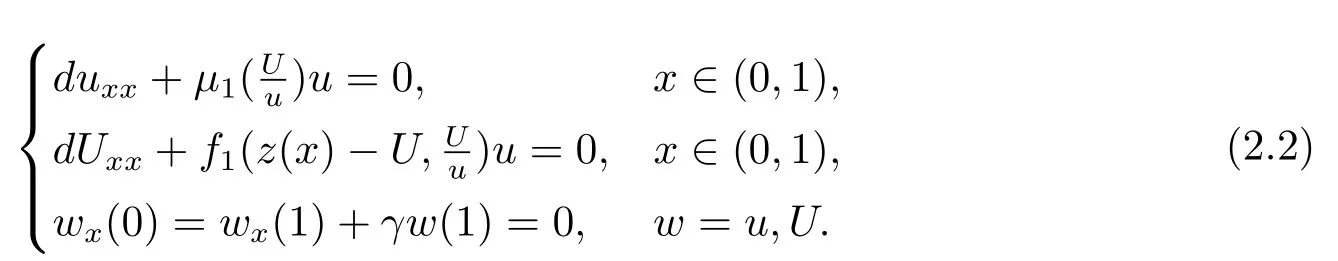



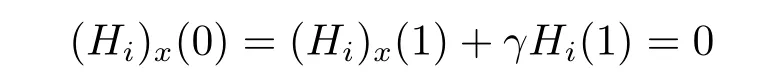
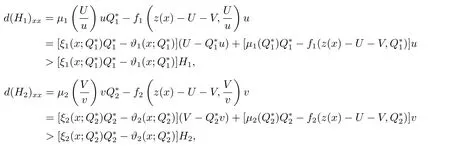
3.正平衡解存在性

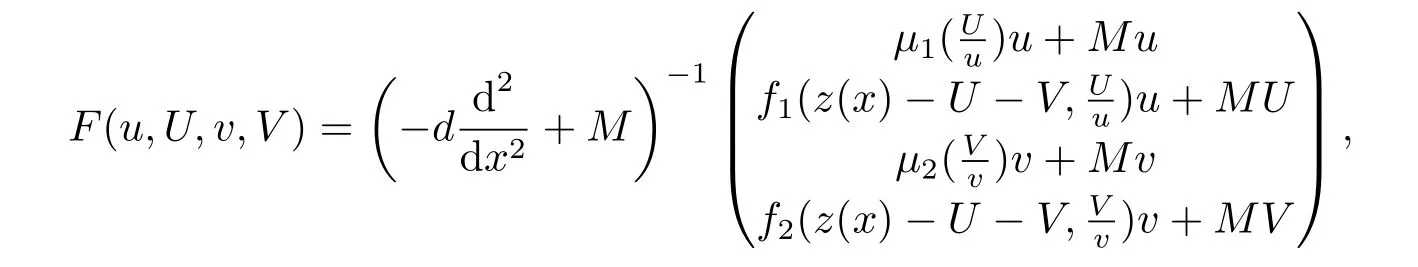
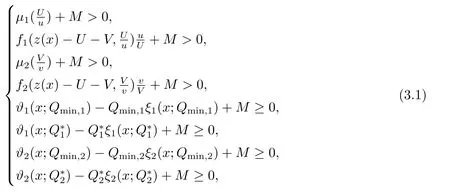

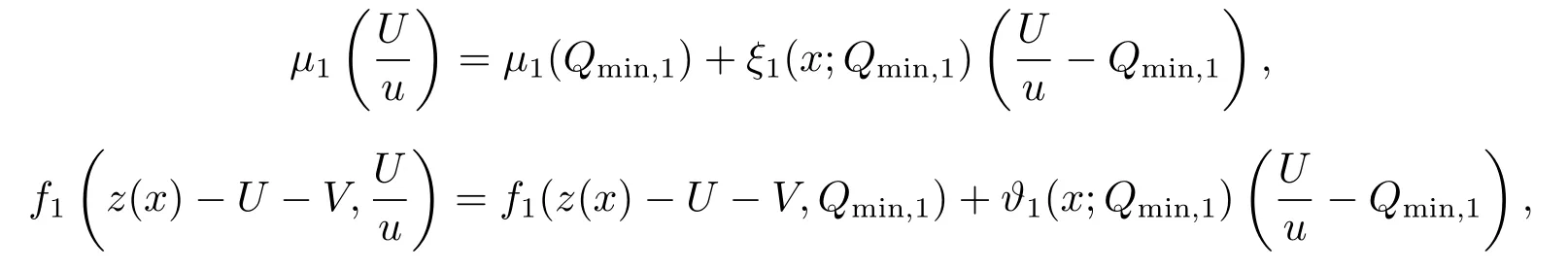
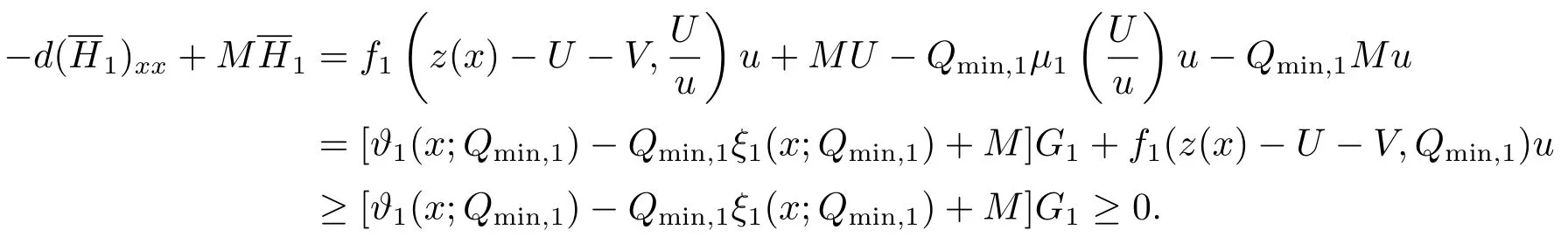






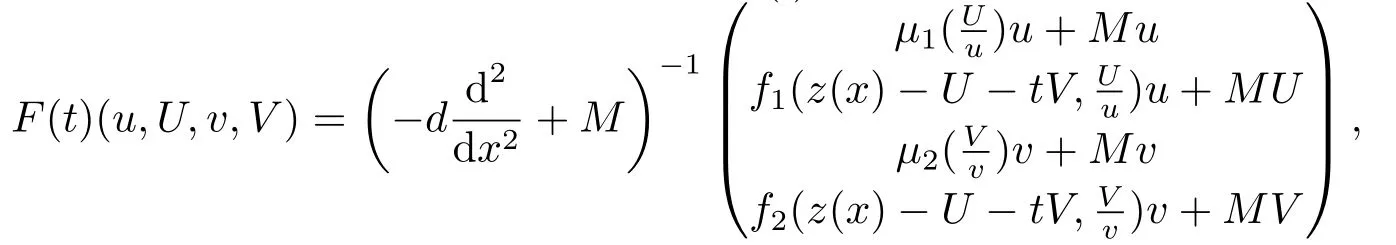

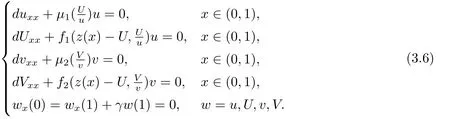

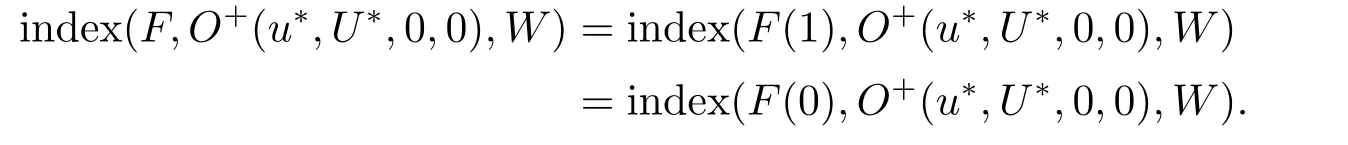






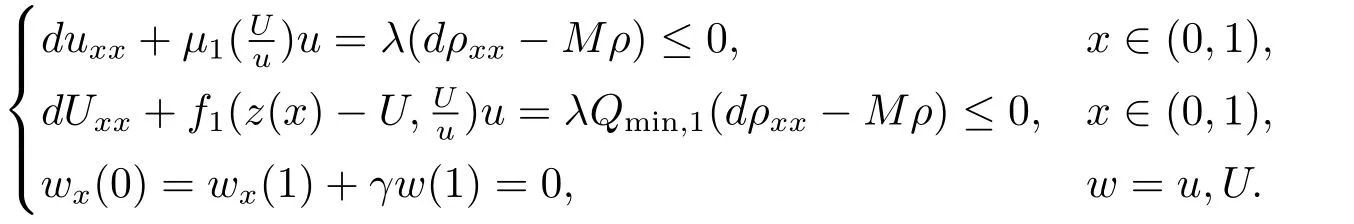

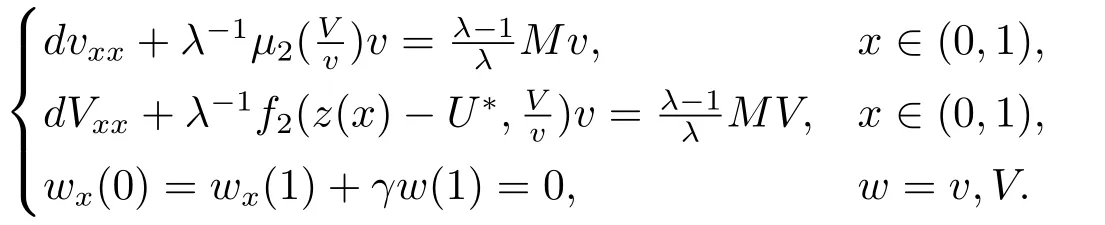






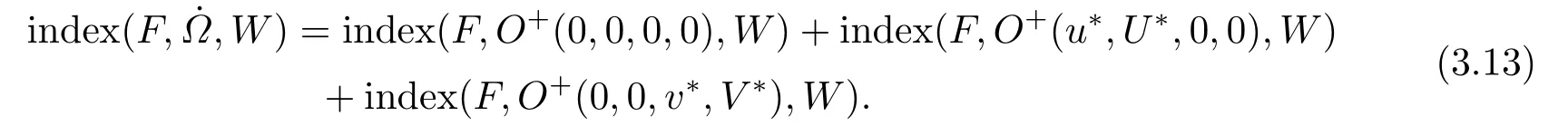

4.总结

