一道平面向量数量积的探究

☉江西师范大学附属中学 胡祝齐

平面向量的数量积的定值或最值问题是平面向量问题中的重点与难点之一，也是新课标大纲在“知识点交汇处”命题的充分体现的一大阵地.此类问题往往设置巧妙，形式活泼多样，条件中知识交汇点众多，题目难度往往比较大，同时解决问题的思维方式多变，破解方法也多种多样，一直是历年高考、竞赛命题中的基本考点和热点之一.

一、问题呈现

【问题】如图1所示，在△PAB中，PA=2，PB=1，在△PAB所在的平面内，以AB为边向三角形外作正方形ABCD，则的取值范围是______.

本题以平面几何为问题背景，借助三角形中的条件以及正方形的构造，进而求解相应的平面向量的数量积的取值范围问题.充分交汇平面几何、平面向量、解三角形、解析几何、三角函数等相关知识，是一道极具特色的问题.

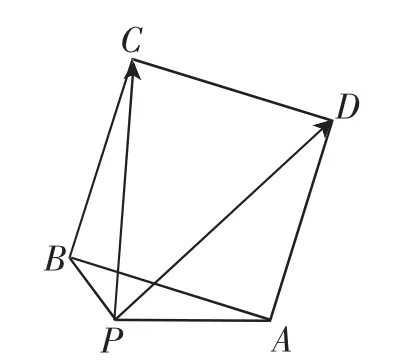
图1

二、多解思维

设出正方形ABCD的边长a，以及∠APB=θ（θ∈（0，π）），通过解三角形中的正弦定理与余弦定理来转化，进而建立相应的关系式，借助平面向量的线性关系来转化对应的平面向量的数量积，再转化为关于θ的三角关系式，通过三角函数的图像与性质来确定相应的最值即可.

解法1：设正方形ABCD的边长为a，设∠APB=θ（θ∈（0，π））.

由余弦定理可得a2=4+1-2×2×1×cosθ=5-4cosθ.

以A为坐标原点，AP所在的直线为x轴建立平面直角坐标系xAy，把对应的平面向量利用坐标加以表示，从而相应的数量积也可用坐标表示出来，再通过三角换元，借助三角函数的图像与性质来确定最值；或通过点与圆的位置关系，借助数形结合来确定最值.

解法2：如图2所示，以A为坐标原点，AP所在的直线为x轴建立平面直角坐标系xAy，则A（0，0），P（-2，0），设B（x，y），则D（y，-x）.

根据正方形ABCD中的对角线AC与BD的中点重合的性质，可得C（x+y，-x+y）.

由于PB=1，则有（x+2）2+y2=1（y＞0）.

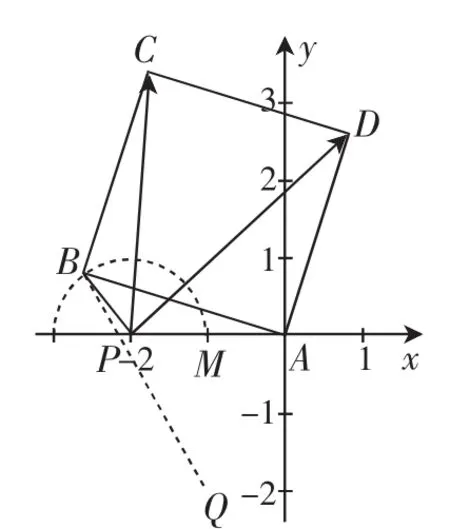
图2

点B满足半圆：（x+2）2+y2=1（y＞0）.

结合图形可知BQ2的最大值为（PQ+r）2=，BQ2的最小值为QM2=22=4（此时点M（-1，0），而y＞0，则最小值取不到）.

所以BQ2-1∈（的取值范围是

三、变式探究

探究1：保留原问题的条件，改变原来构造正方形为构造等腰直角三角形，同时把求解平面向量的数量积问题转化为求解线段的长度问题，得以变式创新.

【变式1】如图3所示，在△PAB 中 ，PA=2，PB=1，在△PAB所在的平面内，以A为直角顶点向三角形外作等腰直角△ABD，则PD的取值范围是______.

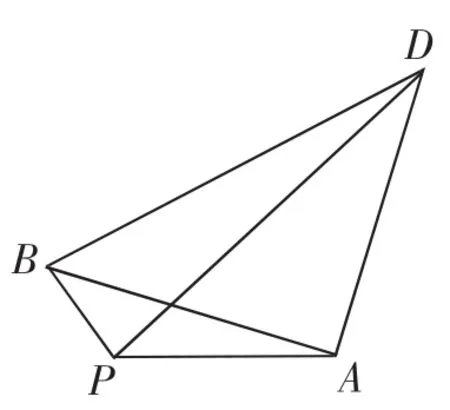
图3

解析：本题的破解方法比较多，借助以上问题的破解方法来处理如下：

如图4所示，以A为坐标原点，AP所在的直线为x轴建立平面直角坐标系xAy，则A（0，0），P（-2，0），设B（x，y），则D（y，-x）.

由于PB=1，则有（x+2）2+y2=1（y＞0）.

那么PD2=（y+2）2+x2=BQ2，其中定点Q（0，-2）.

图4

而点B满足半圆：（x+2）2+y2=1（y＞0）.

结合图形可知BQ2的最大值为（PQ+r）2=，BQ2的最小值为QM2=12+22=5（此时点M（-1，0），而y＞0，则最小值取不到）.

所以BQ2即PD的取值范围是

探究2：保留原问题的条件，改变原来构造正方形为构造等腰直角三角形，同时引入线段的中线，同样求解平面向量的数量积的取值范围问题，得以变式创新.

【变式2】如图5所示，在△PAB中，PA=2，PB=1，C为线段AB的中点，在△PAB所在的平面内，以A为直角顶点向三角形外作等腰直角△ABD，则的取值范围是______.

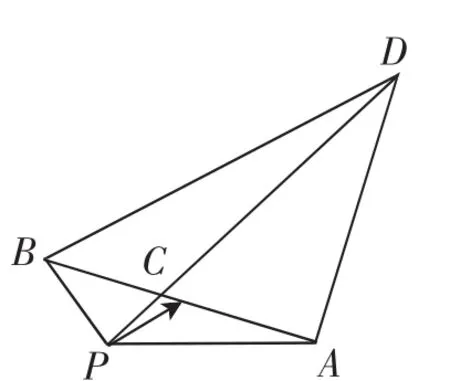
图5

解析：如图6所示，以A为坐标原点，AP所在的直线为x轴建立平面直角坐标系xAy，则A（0，0），P（-2，0），设B（x，y），则

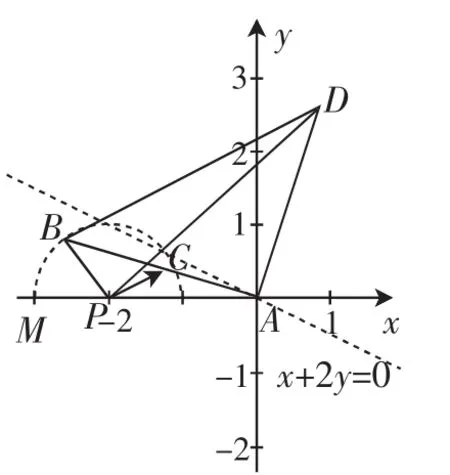
图6

由于PB=1，则有（x+2）2+y2=1（y＞0）.

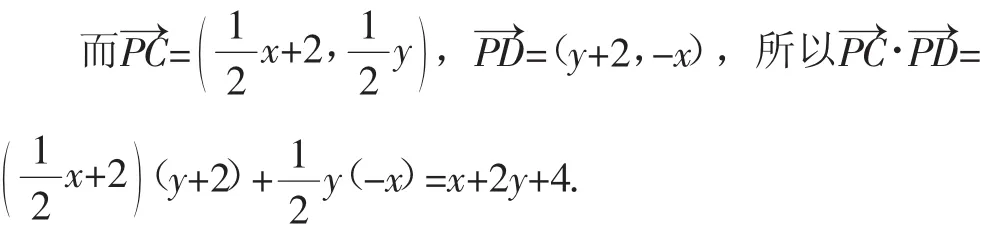
设z=x+2y，作出直线x+2y=0.

由数形结合可知，当直线z=x+2y满足与点B所在的半圆：（x+2）2+y2=1（y＞0）相切时负值舍去）；

当直线z=x+2y过点M（-3，0）时，z取得最小值-3+2×0=-3，而y＞0，则最小值取不到.

四、规律总结

涉及平面几何与平面向量的交汇与综合问题，可以借助解三角形法来处理，也可以利用坐标法，通过建立平面直角坐标系，借助解析几何来分析与处理.特别是用坐标法来处理平面向量问题时，巧妙地把几何问题转化为代数问题，通过代数运算及解析几何本身所具有的特点来处理，从而加强对相关内容的有效综合与合理转化，进而加以正确地理解与掌握相关的知识与破解的方法，这样有助于数学解题能力与应用能力的提高，真正提升数学能力，拓展数学素养.