基于数学抽象的培养与提升

☉江苏省张家港市沙洲中学 施利文

一、问题的提出

在《普通高中数学课程标准（2017年版）》一文中，对于“课程基本理念”这一部分第一次创新性地提出：“高中数学课程以学生发展为本，落实立德树人根本任务，培育科学精神和创新意识，提升数学学科核心素养”.高中阶段，结合数学学科的特点，归纳总结出了六大核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.

其中，对于数学抽象这一重要的核心素养，其是指舍去事物的一切物理属性，进而得到数学研究对象的素养.数学抽象是数学学科的基本思想，也是一种特殊素养，是贯穿于整个数学教学与学习的一条隐形思维链条.那么如何在数学教学、数学学习及数学解题的过程中进行有效、合理、科学地培养与提升学生的数学抽象呢？

二、问题的解决

1.从概念入手进行数学抽象

数学概念是对具体的数学问题进行抽象与概括，从实际问题中区分、抽象、归纳、总结出研究对象的本质特征，通过合理抽象、科学概括、合理归纳，从而得以认识和理解所研究的数学对象与数学问题，最后再结合相关的数学知识与数学方法来进行分析与处理.

例1（2019届江苏省常州市武进区高三第一学期期中考试·14）若正实数x，y满足x2-xy+y2=9，且|x2-y2|＜9，则xy的取值范围为______.

分析：根据条件引入参数，利用双变量换元法进行处理，把取值范围问题转化为对应的不等式问题，通过求解相应的二次不等式来求解对应的代数式的取值范围，即可确定xy的取值范围.

解：设x-y=m，xy=n＞0.

由x2-xy+y2=9，整理有（x-y）2+xy=9，可得m2+n=9，从而n=9-m2≤9.

又|x2-y2|2=（x+y）2（x-y）2=［（x-y）2+4xy］（x-y）2=（m2+4n）m2＜81，

所以将m2=9-n代入，整理有（9+3n）（9-n）＜81，解得n＜0（舍去）或n＞6.

综上所述，n∈（6，9］，即xy∈（6，9］.

故填答案：（6，9］.

点评：涉及代数式相关值的求解或取值范围问题，经常通过引入参数来处理与转化.结合题目条件，通过数学抽象，借助参数的引入并赋值，再利用参数的运算，通过待定系数法的应用，借助二次不等式的求解来达到确定相应的代数式的取值范围的目的.在函数与方程的有效转化与综合的过程中，巧妙地渗透着数学抽象思维及其应用.

2.从公式入手进行数学抽象

数学公式是从数学过程中抽象并归纳出来的，利用数量关系、参数关系、逻辑关系及其他相应关系总结与归纳出来的.因此利用数学公式中所包含的数学抽象来破解相应的数学问题，也是数学抽象的反馈与应用.

例2（2018·全国Ⅱ理·15）已知sinα+cosβ=1，cosα+sinβ=0，则sin（α+β）=______.

分析：借助条件给出两个相应的三角函数的关系式，利用三角函数公式，通过具体的特殊角加以特殊化处理，先入为主，进而在特殊角的情况下确定相应的三角函数值的取值.

解：根据填空题的特征，其答案具有一般性——定值，那么可以借助三角函数公式，取特殊角来处理：α=150°，β=60°.

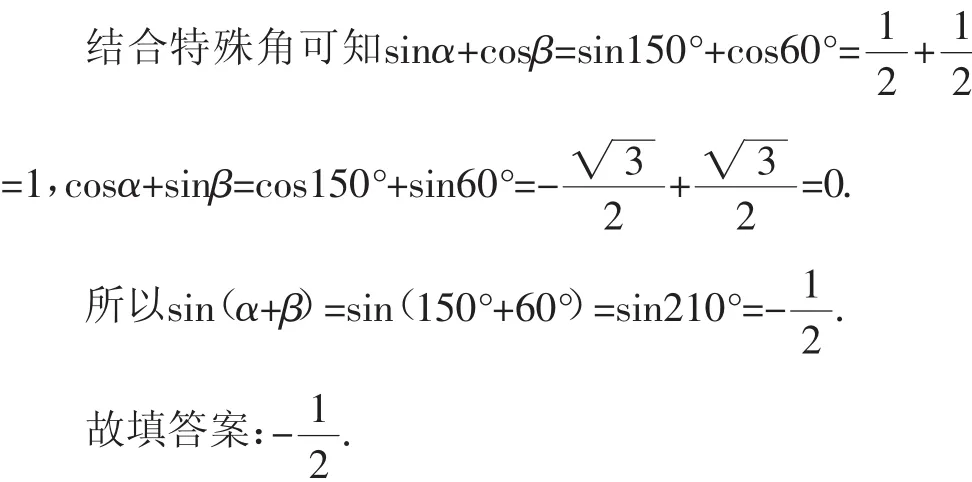
点评：借助三角函数公式，以特殊代表一般，进而达到求解的目的.在处理一些选择题或填空题时，经常借助数学公式加以数学抽象，先入为主，巧妙地构造满足公式的特殊值来进行转化与处理，达到以特殊代表一般的目的.从而巧妙地省去中间的三角恒等变换，简化运算，提升效益.

3.从图形入手进行数学抽象

从数学图形中反映并抽象出数学概念、数学数量、数学参数等之间的关系，以及变化规律、基本性质等.借助数学图形，可以从中抽象出一般性的规律与结构，进而为破解数学问题指明方向与提供条件.

例3孔明锁，也叫鲁班锁，是广泛流传于中国民间的智力玩具，起源于古代汉族建筑中首创的榫卯结构.图1是六柱孔明锁，由6根相同的开槽（即榫卯结构）的正四棱柱组合而成.图2中的边长为1的正方形网络中粗线画出的是该六柱孔明锁的正视图，则该六柱孔明锁的表面积为______.

图1

图2

分析：借助数学文化的阐述，对于复杂图形的表面积问题，可以借助于三视图中的投影图形加以数学抽象并进行归纳总结，利用投影面积的计算来达到目的.

解：由六柱孔明锁的正视图可知，投影面积为10×4+2×3×2=52.

而六柱孔明锁的所有表面共由6个投影面组成，所以该六柱孔明锁的表面积为52×6=312.

故填答案：312.

点评：借助对数学图形的分析、归纳并加以抽象，明确给出六柱孔明锁的所有表面是由6个投影面所组成的，且每一个投影面都与正视图中的投影面相吻合，因此通过数学抽象总结归纳出规律进行破解.

4.从方法入手进行数学抽象

数学方法是借助于数学知识来归纳并总结出具有可操作性、可拓展性的破解问题的基本思维方式，是数学抽象的具体体现方式之一，也是数学抽象的具体体现、高度概括、方法类比、准确表达及思维应用等系统性的体现.可以通过数学抽象出来的数学方法来有效地解决问题，提升能力.

例4 （2019届江苏省盐城市高三期中考试·12）已知函数f（x）=（x+m）-（m+1）x在R上单调递增，则实数m的取值集合为______.

分析：涉及函数的单调性问题，往往从导数方法入手，利用导数的求解，结合不等式恒成立加以数学抽象，进而达到破解参数的取值范围的目的.

解：由题可知f′（x）=（x+1+m）ex-x-（m+1）=（x+1+m）·（ex-1）≥0在R上恒成立.

当x≤0时，ex-1≤0，则必须x+1+m≤0恒成立，解得m≤-1；

当x＞0时，ex-1＞0，则必须x+1+m≥0恒成立，解得m≥-1.

综上可得m=-1.

故填答案：{-1}.

点评：不同的数学知识具有比较常规的数学方法，而有关函数的单调性问题，一般采用导数法来破解.借助数学抽象所归纳出来的数学方法来进行破解，是解决数学问题的首选，也是常规解题规律的首选.

三、感悟与反思

其实，数学核心素养并非是另起炉灶的“新搞法”、“新噱头”，而是解决数学问题所必须具备的核心知识、基本技能技巧，以及与之相关的数学运算能力、逻辑推理能力、抽象与想象能力，还有遇见问题时的思维方式和解决问题时的基本模式.

数学抽象是通过对高中数学课程的教学与学习，逐步抽象出相应的数学概念、公式、命题、图形、方法和体系等，养成思考问题的一般性习惯，并进一步归纳总结，进而把握数学问题的本质属性，达到抽象概括、化繁为简的目的，从而有效地借助数学抽象的核心素养与思维方式来思考、分析与解决问题.