谈数学核心素养在高考命题中的体现

☉江苏省苏州实验中学 朱仁林

一、问题提出

教育部考试中心在2018年与2019年的高考数学考试大纲中，着重明确了高考“考什么”与“怎么考”，其中“考什么”主要包括：必备知识、关键能力、学科素养、核心价值.

教育部发布了《普通高中课程方案和各科课程标准》，此次课程标准在原有的基础上进一步完善，并作了较大幅度的修订，且首次正式凝练并科学地提出了“学科核心素养”的说法与具体要求.

对学科核心素养的考查，在2018年的高考中已经得到初步尝试.那么在今后的高考中，学科核心素养的考查仍然是高考的重要内容与方向之一.那么，高考数学学科的核心素养是什么？它们在高考试题中怎样呈现并考查的呢？对复习备考有哪些要求？这是我们关注的重点内容.

二、数学核心素养怎么考

数学核心素养包括数学抽象、逻辑推理、直观想象、数学建模、数学运算、数据分析.主要表现在用数学的眼光去观察世界，用数学的思维去分析世界，用数学的语言去表达现实世界.

1.数学抽象

数学抽象素养，其实就是通过具体的实例概括出一般性的结论.数学抽象的过程就是在综合的问题情境中学会抽象出相应的数学问题，并在所抽象出来的数学结论的基础上，进一步归纳形成新的命题.

例1（2018·全国卷Ⅱ）已知f（x）是定义域为（-∞，+∞）的奇函数，满足f（1-x）=f（1+x）.若f（1）=2，则f（1）+f（2）+f（3）+…+f（50）=（）.

A.-50 B.0 C.2 D.50

命题立意：本题主要考查函数的奇偶性和周期性，旨在考查学生探究数学本质的能力.

解析：因为f（x）是定义域为（-∞，+∞）的奇函数，且f（1-x）=f（1+x），所以f（1+x）=-f（x-1）.所以f（3+x）=-f（x+1）=f（x-1）.所以T=4.

因此f（1）+f（2）+f（3）+…+f（50）=12［f（1）+f（2）+f（3）+f（4）］+f（1）+f（2），由f（1）=2，得f（-1）=-2，f（3）=-2.又因为f（x）为奇函数，所以f（0）=0.所以f（2）=f（4）=0.所以f（1）+f（2）+f（3）+f（4）=0，从而f（1）+f（2）+f（3）+…+f（50）=f（1）=2.故选C.

2.逻辑推理

逻辑推理素养，其实就是提出问题和论证命题的过程.逻辑推理的过程就是科学地选择合适的论证方法与推理途径并予以论述与证明，并在此基础上能用准确、严谨、简单的数学语言表述并论证相应的过程.

图1

命题立意：本题主要考查双曲线的几何性质、直线与直线的位置关系，以及学生的数形结合思想、化归与转化思想，推理论述能力与运算求解能力，考查的核心素养是逻辑推理和数学运算.

解析：因为双曲线的渐近线方程为y=所以∠MON=60°，不妨设过点F的直线与直线交于点M.由△OMN为直角三角形，不妨设∠OMN=90°，则∠MFO=60°.又直线MN过点F（2，0），所以直线MN的方程为

3.直观想象

直观想象素养，其实就是通过对平面图形或空间图形的观察与想象，以及图形与数量之间关系规律的分析，利用数学想象对复杂的数学问题进行有效的直观表达.直观想象就是运用图形与空间的想象来分析与处理问题，感悟事物的本质属性，形成解决问题的思路与方法.

例3 （2018·河南新乡一模）如图2，网格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，其中俯视图中的两段圆弧均为半圆，该几何体的体积为（ ）.

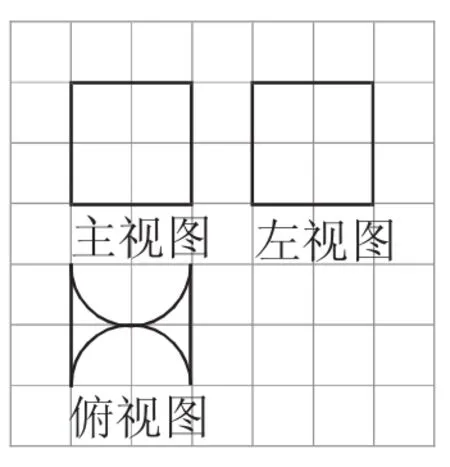
图2

命题立意：本题主要考查三视图、空间几何体的位置关系及空间几何体的体积问题，考查数形结合思想、空间想象能力及运算求解能力，考查的数学核心素养是直观想象.

解析：由三视图可知，该几何体是由正方体挖去两个半圆柱后形成的.如图3所示，所以该几何体的体积为2×2×2-π×12×2=8-2π.故选C.

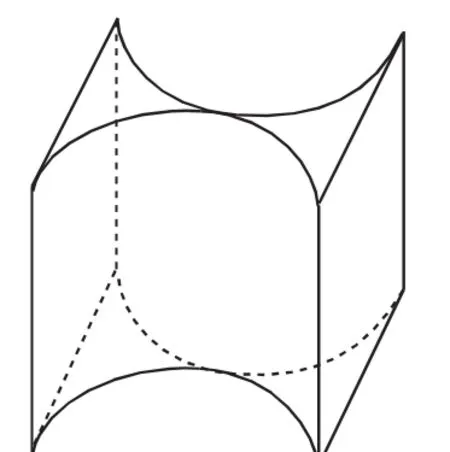
图3

4.数学建模

数学建模素养，其实就是通过对实际应用问题的处理，运用数学语言，清晰、准确且有效地表达数学建模的过程和结果.

例4（2018·河北名校联考）在正整数数列中，由1开始依次按如下规则，将某些数染成红色.先染1；再染两个偶数2，4；再染4后面最邻近的3个连续奇数5，7，9；再染9后面的最邻近的4个连续偶数10，12，14，16；再染此后最邻近的5个连续奇数17，19，21，23，25.按此规则一直染下去，得到一红色子数列1，2，4，5，7，9，10，12，14，16，17，…，则在这个红色子数列中，由1开始的第2018个数是（ ）.

A.3971 B.3972 C.3973 D.3974

命题立意：本题以“红色子数列”为背景，巧妙地将数字游戏与数学中的数列结合在一起，综合考查考生的化归与转化思想、阅读理解能力、运算求解能力，以及分析问题、解决问题和处理问题的能力，考查的核心素养是数学建模.

解析：由题意可知，第1组有1个数，第2组有2个数，…，根据等差数列的前n项和公式，可知前n组共有个数.

三、复习备考

1.要重视数学基本概念的复习

从数学概念的定义层面出发，由表及里，去伪存真，正确掌握数学基本概念的本质属性，这是提升数学素养的最基本的必要条件，也是提升数学素养的基石.因此在概念复习中要避免模式化，避免机械套用有关结论.

2.要重视数学基本定理、公式的来龙去脉

我们知道，学生当中普遍存在数学基本定理、公式“重应用轻推导”的现象，往往只重视数学基本定理、公式的应用，而忽视数学基本定理、公式的由来、推导过程以及定理的证明等.但事实上，重视数学基本定理、公式的由来、推导过程，以及定理的证明等，不仅有利于理解与掌握数学基本定理、公式，以及理解公式之间的相互关系，还可以进一步挖掘数学基本定理、公式中所蕴含的数学思想和基本技能，从而成为我们解决有关数学问题的“模板”，特别是解决一些创新型问题的敲门砖.

3.要重视数学基本技能的应用

数学基本技能是数学基础知识的重要组成部分之一，在相应的数学建模、数学运算及数据分析等数学核心素养中都有它的影子，也是数学问题中比较常见的考查方式之一.数学基本技能是历年高考数学考查的重点之一，因此对数学基本技能的复习，要引起高度重视，可以从掌握入手点、了解隐藏点与熟悉易错点等角度切入来进行有效复习.

4.要重视中国古代数学文化

近几年的高考试题增加了对中国传统文化的考查，常见的方式是将中国古代文化作为试题的背景材料，融合相应的数学知识来设置创新型问题，既可以有效地考查学生对知识的理解与掌握情况，还可以充分体现出中国传统文化对人类发展和社会进步所做出的贡献.同时，此类题目往往难度不大，立意新颖，富有创新性，特别是巧妙地利用我国或世界的优秀传统文化设计试题，不仅使学生对我国或世界的传统文化有所了解，同时也考查了学生各方面的能力，很好地渗透了数学核心素养.