分块稀疏自适应滤波算法研究

鲁振姣，郭 莹

（沈阳工业大学信息科学与工程学院,沈阳110870）

1 引 言

自适应滤波算法研究已经成为当今信号与信息处理领域的热点，算法直接影响滤波效果的好坏[1]。如文献[2]所提出的仿射投影算法（Affine Projection Algorithm,APA）及其改进算法是一类重要的自适应滤波算法，该类算法在输入信号相关性较高的情况下仍具有良好的收敛性能。但是许多系统的脉冲响应是稀疏的，即它们的脉冲响应绝大部分为零或者是很小的值，一小部分的脉冲响应具有显著幅度。文献[3]的成比例仿射投影算法（Proportionnate APA,PAPA,）就是针对稀疏系统提出的，其原理是每个系数通过采用滤波器抽头权重成比例的独步来加快收敛速度，即滤波器抽头权重系数越大，步长越大，抽头系数越小，步长越小。成比例算法有效的利用了未知系统的稀疏特性，使算法的收敛速度显著提高。

但是，在很多实际应用系统中，例如网络回声消除和卫星连接通信回声消除，它们的脉冲响应是成块出现的，其余值为零值或者很小的数，即它们的系统稀疏特性是呈现为成块的形式。分块稀疏是最常见也是最简单的的一种稀疏结构，分块稀疏意味着稀疏信号中的非零元不再是出现在任意位置，而是成块出现。因此有必要将块稀疏性这个问题考虑到传统的自适应滤波算法中，使用具有块稀疏脉冲响应的自适应滤波器对此类稀疏系统进行建模，根据不同情况提出相应的块稀疏自适应滤波算法。

然而PAPA 算法没有考虑未知系统的块稀疏特性，针对分块稀疏的系统信道，收敛速度并没有显著提升。所以针对这一特性，文献[4]提出的块稀疏自适应滤波算法，进一步加快了收敛速度。该算法的原理是：在计算对应的步长因子时，用混合l2,1范数约束代替传统的l1范数约束。这样的约束有效地利用了未知系统的块分布特性，将自适应滤波权重比例系数分块处理，对于成块出现的脉冲响应分配大的系数，其余的分配小的系数，使算法速度显著提升。

为验证并对比以上算法的性能，将理论分析与仿真相结合进行研究，结果表明块稀疏自适应滤波算法有较好的收敛性能。

2 算法分析

2.1 APA算法

以系统辨识[5]为例来分析各类自适应滤波算法的性能。图1 为自适应滤波器系统辨识原理图。

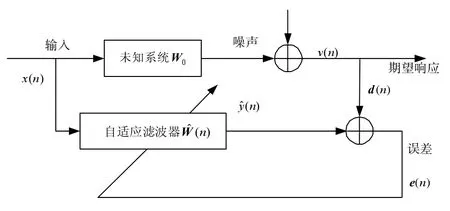
图1 自适应滤波器系统辨识原理图

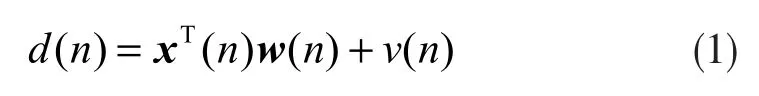
设先验输出误差向量为：

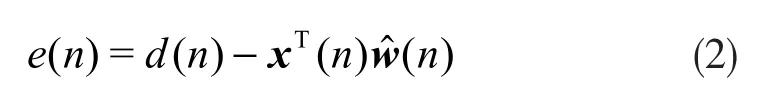
APA 算法利用增加输入信号矩阵的维度对数据进行重用，以改善收敛性能，这里的维度称为投影阶数M ，所以APA 算法的输入为：

由于有数据重用，那么输出向量y(n)可以表示如下：

得到的期望响应d(n)可用如下线性模型表示：

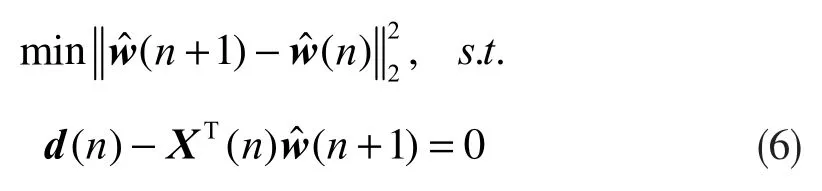
利用拉格朗日乘子方法，可将带约束条件最优化问题转化为无约束最优化问题，即：

令式(8)的导数值为零，得：

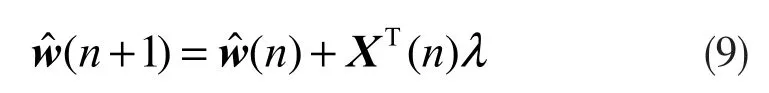
将式(9)代入式(6)中的约束条件，得：

将式(10)代入式(9)中可得APA 算法的权系数向量更新公式，并引入步长因子μ，可得：

为了防止自相关X(n)XT(n)太小，算法中还可以引入一个非常小的正整数，令APA 算法的权系数向量更新公式变为如下形式：

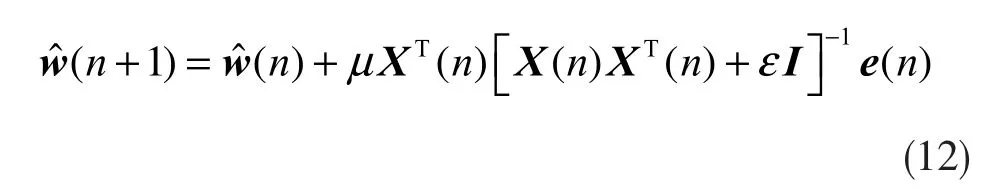
其中，ε 是正则化因子，I 为 M×M 的单位矩阵，εI是为避免对不满秩方阵求逆而添加的一个对角矩阵。

2.2 PAPA算法

PAPA 算法的滤波器系数更新公式可由如下约束最优化问题获得：

使得系数更新后的误差向量等于零，则有：

利用拉格朗日乘子法，得到PAPA 的系数向量更新方程：

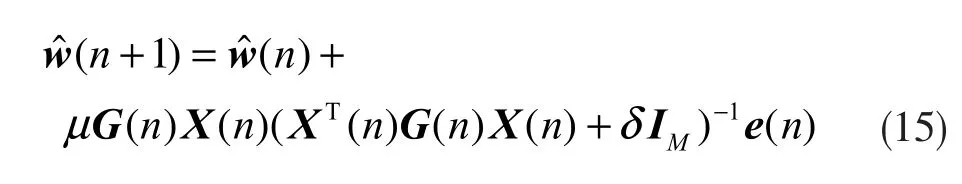
其中，μ 是步长参数，δ 是正则化参数，IM是 M×M 单位矩阵，并且有：

其中，q 是一个很小的正数，它用来在初始阶段所有滤波器系数都为0 时启动更新，并且防止所有参数都为0 时算法冻结。ρ 用于当某个系数过小时防止该系数不更新。

PAPA 虽具有快速初始收敛速度，但其后期收敛速度缓慢。此外，如果脉冲响应稀疏性不够高，其收敛速度会大大降低。针对这些问题，基于μ 规则的PAPA（μ-law PAPA,MPAPA）算法[5]被提出。

2.3 MPAPA算法

MPAPA 算法是通过定量分析自适应滤波器系数的收敛过程，来得到最优的比例步长计算方法。MPAPA 的比例步长参数计算方法注重大、小系数之间的平衡，使大、小系数同时收敛于最优值，克服了PAPA 过分强调大系数收敛的缺点。因此，MPAPA从根本上解决PAPA 后期收敛速度缓慢的问题。MPAPA 算法的比例步长矩阵G(n)可用如下一组公式进行描述：

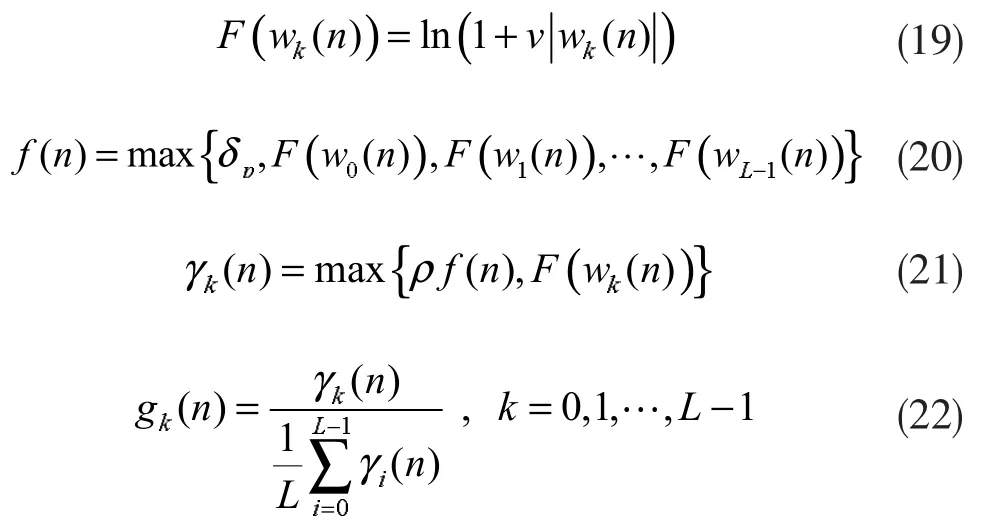
2.4 BS-PAPA算法

然而，MPAPA 并没有考虑块稀疏特性。由块稀疏 PNLMS（BS-PNLMS）算法推动，文献[4]提出了一系列新的块稀疏PAPA（BS-PAPA）算法，进一步提高了其在块稀疏脉冲系统下的识别性能。

BS-PAPA 将l2,1范数引入到成本函数中，从而使优化问题转变为：

进而使得系数更新后的误差向量等于零：

根据文献[6]、[7]，可知：

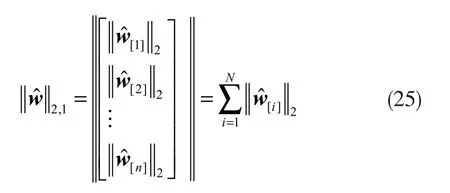
利用拉格朗日乘子法，可以得到的BS-PAPA的系数向量更新方程：

其中：

当 P ＝ 1 时，BS-PAPA 算法等同于 PAPA 算法;当 P＝L 时，BS-PAPA 算法等同于 APA 算法。

3 仿真实验

3.1 仿真条件

仿真中输入的有色信号均由零均值高斯白噪声通过一阶AR 系统产生，这里假设自适应滤波器的长度和未知系统的长度相等，均为120。

实验中各个算法的投影阶数M ＝4，BS-PAPA算法中的块数P＝4，且算法的比较都在公平原则下进行。每个仿真均是30 次实验的平均结果，且迭代次数为20000 次。信道由图2所示，使用两种块稀疏信道，其中图2(a)为单簇块稀疏信道，图2(b)为双簇块稀疏信道。

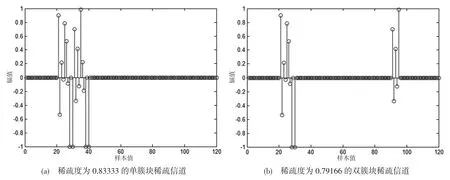
图2 仿真实验选用的信道

3.2 性能指标及参数设置

实验是使算法在等效步长的条件下，以归一化均方偏差（Normalized MSD,NMSD）的收敛曲线来评价算法的收敛性能，即利用NMSD 来度量自适应滤波器与目标系统的逼近程度。

仿真参数是在等效步长[8]的条件下设定的，具体如表1所示。

表1 实验中的参数设置

3.3 仿真结果与分析

将需要仿真的算法应用到系统辨识系统中，仿真实验采用MATLAB 进行，步骤如下：

1）在单簇块稀疏信道中比较各算法性能

各算法在单簇块稀疏信道中的仿真对比结果由图3所示。可见，PAPA 算法在稀疏信道中收敛速度明显优于APA 算法；MPAPA 算法比PAPA 算法收敛速度加强；BS-PAPA 算法由于是在块稀疏信道中，收敛速度明显优于PAPA 算法和MPAPA 算法。

2）比较各类算法在双信道中的跟踪性能

图4所示为 APA 算法、PAPA 算法、MPAPA 算法和BS-PAPA 算法分别在单簇块稀疏信道与双簇块稀疏信道下的跟踪性能比较图。当迭代次数n≤20000 时，所使用的信道是稀疏度为0.83333 的单簇块稀疏信道（对应图2(a)）；当迭代次数n ≥20000时，所使用的信道是稀疏度为0.79166 的双簇块稀疏信道（对应图2(b)）。由图4 中可以看出，BS-PAPA算法在信道突变时仍具有稳定的跟踪性能，相比其他算法更为优越。

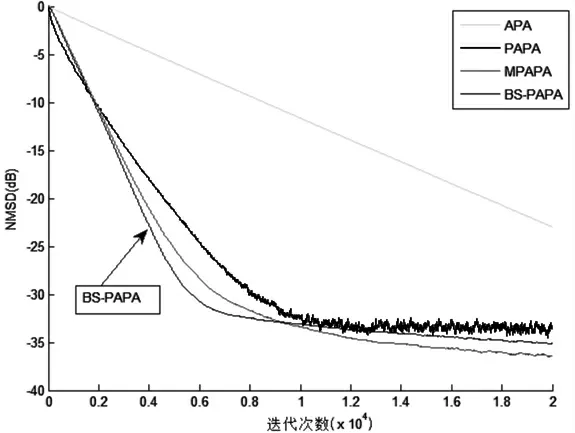
图3 各算法在单簇块稀疏信道中的性能比较

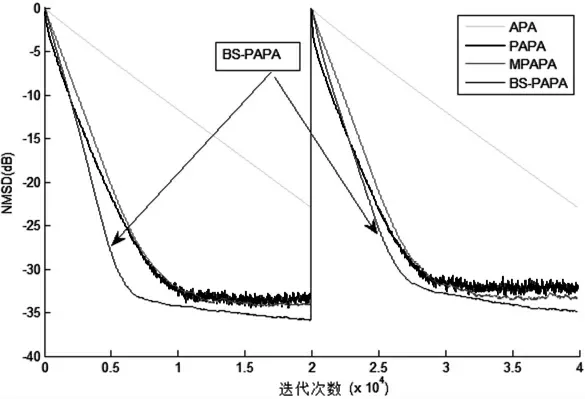
图4 各算法在不同信道下的跟踪性能比较

3) BS-PAPA 算法不同块数与PAPA 算法比较

图5 为 PAPA 算法、P=3 的 BS-PAPA 算法、P=4 的 BS-PAPA 算法和 P=10 的 BS-PAPA 算法分别在单簇块稀疏信道与双簇块稀疏信道下的跟踪性能比较图。当迭代次数n≤10000 时，所使用的信道是稀疏度为0.83333 的单簇块稀疏信道（对应图2(a)），当迭代次数 n ≥10000 时，所使用的信道是稀疏度为0.79166 的双簇块稀疏信道（对应图2(b)）。

图5 BS-PAPA 算法不同块数与PAPA 算法比较

由图5 可以看出，BS-PAPA 算法在块稀疏信道中收敛速度明显优于PAPA 算法，且不同的块数影响BS-PAPA 算法的收敛速度。对于此次仿真，块数P=4 时，收敛速度最快。

4 结束语

分块稀疏自适应滤波算法利用了块稀疏信道这一特质，加快了算法的收敛特性。与传统的稀疏自适应滤波算法相比有较快的收敛性和跟踪性能。通过计算机仿真实验也表明块稀疏算法在分块稀疏信道中具有更佳的收敛速度。