新型光学检测靶标静态指向误差修正

张绍军， 薛向尧， 高云国， 王光

(1.中国科学院 长春光学精密机械与物理研究所， 吉林 长春 130033； 2.中国科学院大学， 北京 100049)

0 引言

光学检测靶标是一款特种检测设备，用于室内检测光电跟踪测量设备的技术性能，因此在光电跟踪测量设备研制过程中，光学检测靶标起着重要作用[1]。

当前，专用于室内检测光电跟踪测量设备性能的检测设备主要有固定式检测架、一维动态旋转靶标和二维旋转靶标。固定式检测架为静设备，主要功能是检测被检设备的静态测角精度且具有较高的检测精度；一维动态旋转靶标能够生成运动目标，可对被检设备进行跟踪精度和动态测角精度的检测，单自由度运动具有较高的动态检测精度，但模拟目标运动轨迹单一；二维旋转靶标与一维动态靶标的检测功能相同，具有两个运动自由度，可模拟天顶半球面上的多条轨迹[2-3]，但未查阅到与其相关的测试报道，检测精度未知。

为了满足大型车载光电跟踪测量设备的跟踪精度检测，课题组研制了一款三自由度多功能光学检测靶标，后文统称其为检测靶标。就机构方面而言，检测靶标与上述几种靶标存在不同，检测工作开始前，需要保证检测靶标在全工作域内平行光管主光轴线始终能够进入被检测设备的视场角内，即检测靶标必须具有一定的指向精度，否则会影响检测结果的准确性，严重时生成的目标像点不能够导入被检测设备视场内，无法被光电传感器接受，导致设备检测失效，因此空间静态指向精度是检测靶标设计的主要指标之一。为满足视场为10′以上被检设备传感器的使用要求，检测靶标的空间静态指向精度设计指标为±5′.

本文首先介绍了检测靶标的机构，简要分析了引起指向误差的多项主要误差源，利用齐次坐标变换法建立了机构的方位角指向误差和俯仰角指向误差模型，并将这两种指向误差合成机构总的指向误差；其次利用Leica全站仪在工作域内标定出方位角和俯仰角误差试验数据，由数据样本拟合出误差模型中各待定系数；最后采用该模型修正检测靶标机构指向误差，提高系统的静态指向精度。

1 机构简介与误差源分析

1.1 机构简介

如图1所示，检测靶标机构由支撑架、方位轴系、水平直线运动系统、俯仰轴系和目标生成器(即卡塞格林式平行光管)组成。方位轴系在水平面内可进行方位角为[-360°,360°]内旋转运动；水平直线运动系统和俯仰轴系按照一定的运动函数关系式，带动平行光管在俯仰角为30°～60°内旋转运动。当对方位轴和俯仰轴设置不同组合运动参数时，平行光管就能够生成轨迹多样的模拟目标。

1.2 误差源分析

1.2.1 指向误差定义

指向误差定义为平行光管主光轴线实际指向与理想指向的空间夹角。如图2所示，设理想出射光线指向矢量Pi与实际出射光线指向矢量Pa之差为指向误差矢量ΔP，两矢量间的夹角为指向误差θ. 以上各量均为小量，得出(1)式：

(1)

式中：ΔPx、ΔPy分别为指向误差矢量ΔP在x轴方向与y轴方向矢量分量；θA≈ΔPx为方位角误差，A为方位角；θE≈ΔPy为俯仰角误差，E为俯仰角。

1.2.2 误差源

如图3所示，在各构件上建立坐标系并在静态参考坐标系O0x0y0z0下研究指向误差，各误差源的详细分析及坐标系建立过程详见文献[4]。图3中：l0表示滑板沿导轨运动的最大行程；x表示滑板在导轨上由最远端开始移动的位移；A表方位轴转到的方位角；E表示俯仰轴转到的俯仰角；O1x1y1z1表示支撑横梁参考坐标系；O1ax1ay1az1a表示支撑横梁连体坐标系；O2x2y2z2表示方位轴参考坐标系；O2ax2ay2az2a表示方位轴连体坐标系；O3x3y3z3表示导轨连体坐标系；O3ax3ay3az3a表示滑板连体坐标系；O4x4y4z4表示俯仰轴参考坐标系；O4ax4ay4az4a表示俯仰轴连体坐标系；O5x5y5z5表示平行光管连体坐标系；5P表示与x5轴同向的单位矢量。

平行光管的主光轴静态指向误差主要取决于链式机构中各环节误差，其中主要包括以下几个环节误差：

1) 支撑横梁变形误差和调平误差；

2) 方位轴系安装垂直度误差、方位轴回转倾角误差和方位轴电控系统定位误差[5-8]；

3) 大跨距悬臂梁挠曲变形误差；

4) 滑板与导轨运动副间的运动误差[9]；

5) 俯仰轴系安装垂直度误差、俯仰轴回转倾角误差和俯仰轴电控系统定位误差；

6) 平行光管安装误差。

除了以上6种主要误差源外，也存在其他线性误差，这类线性误差对指向误差没有影响。将上述误差分为静态误差与运动误差，静态误差与安装连接过程的精度有关；运动误差取决于运动过程的控制精确度，且是运动控制参数A、E的函数。经误差源分析，共找出23项误差列于表1.

表1 机构误差参数

2 指向误差模型建立

根据第1节的误差源分析，基于齐次坐标变换原理，平行光管连体坐标系O5x5y5z5到参考坐标系O0x0y0z0的总变换矩阵为(2)式:

(2)

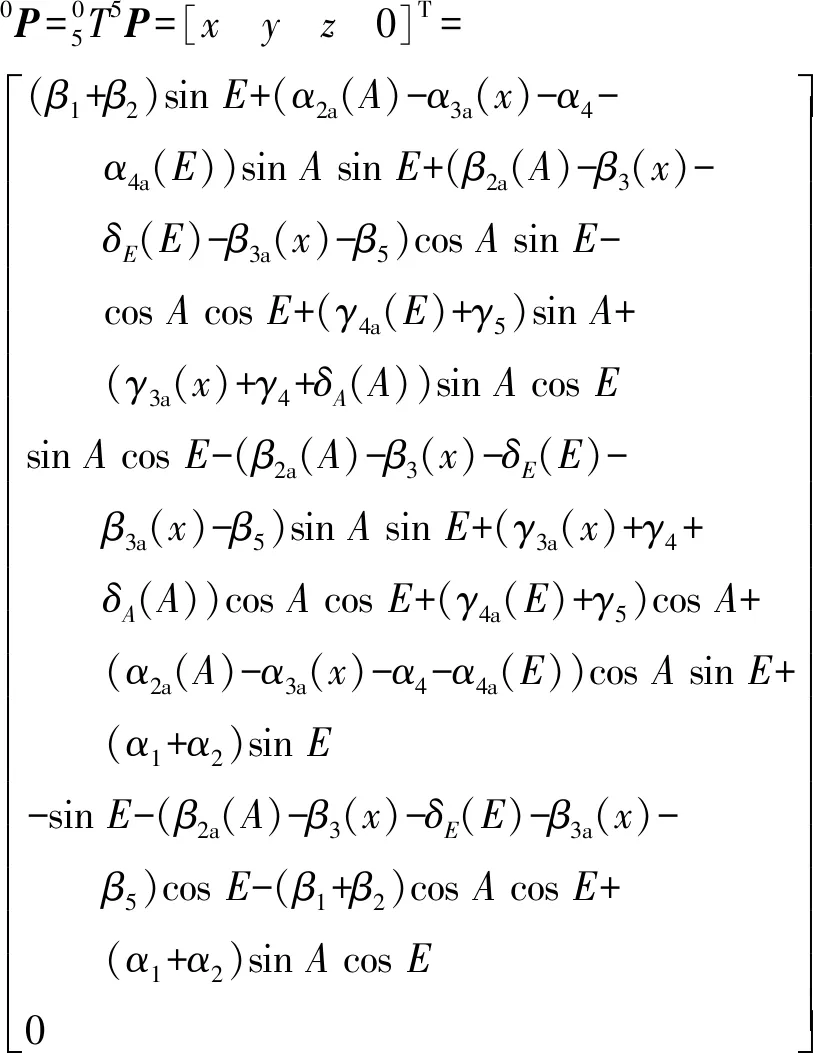
(3)

由图3可知，直角坐标系转换成指向角的计算公式为

(4)

式中：ΔA、ΔE分别表示方位角误差和俯仰角误差。

将(3)式代入(4)式，化简后得到(5)式:

(5)

由(5)式可知，方位角与俯仰角误差主要由安装倾斜角误差、轴系垂直度误差、运动回转角误差，控制定位角误差等角性误差引起，与直线位移误差无关，因此只需对角性误差进行修正即可[10-11]。

3 试验分析

3.1 指向误差标定

利用瑞士徕卡公司生产的Leica-NovaTS50、测角精度为0.5″高精度全站仪作为标定设备，其是相关行业内公认的测角标定设备。如图4所示，通过全站仪机体底部螺纹连接端口将其固定在支撑三脚架上，支撑三脚架通过螺杆可以进行高低调节。

试验步骤如下：

1) 设定检测靶标处于零位姿。在检测靶标工控机上设定平行光管俯仰角为30°、高度差H为920 mm(检测靶标俯仰轴线距全站仪方位轴线在竖直方向上的距离)、方位角为0°.

2) 全站仪位姿对标。理论上，需要保证全站仪方位轴与检测靶标方位轴同轴、全站仪望远镜视轴与平行光管主光轴同轴。全站仪方位轴与俯仰轴轴线位置都标记在机体外壳上，检测靶标方位轴下端与平行光管次镜基座分别安装辅助激光器，检测靶标方位轴线和平行光管主光轴线分别与相应激光器出射光线同轴，因此激光器发出的激光可以作为检测靶标方位轴线与平行光管主光轴线的指示光。借助指示光调节三脚支撑架空间位置及其螺杆升降，在允许误差范围内，可以较容易地保证全站仪三轴交点落到检测靶标方位轴与平行光管主光轴线的交点上。

3) 全站仪调平。步骤2完成后，开机观察显示面板上的电子水准仪，对全站仪水平度进行粗调与微调，直至水平度显示接近0°，此时可认为全站仪处于水平状态。

4) 标定第1个点。调节全站仪望远镜和目镜焦距，使视场中出现清晰明亮的平行光管分划板星点像；精调全站仪方位与俯仰定位旋钮，使明亮星点像落在望远镜分划板十字丝中心。由于检测靶标不做方位方向指北检测，第1个点处方位值可看作起始值，此时记录方位角A与俯仰角E，作为第1个标定值。

5) 标定其余点。方位角在0°～345°，步长15°；俯仰角30°～60°，步长2°，工作域内共24×16=384个标定点。重复步骤4，依次标定。由于标定数据较多，表2仅列出了A=0°～345°、E=44°时24个点处的标定数值。

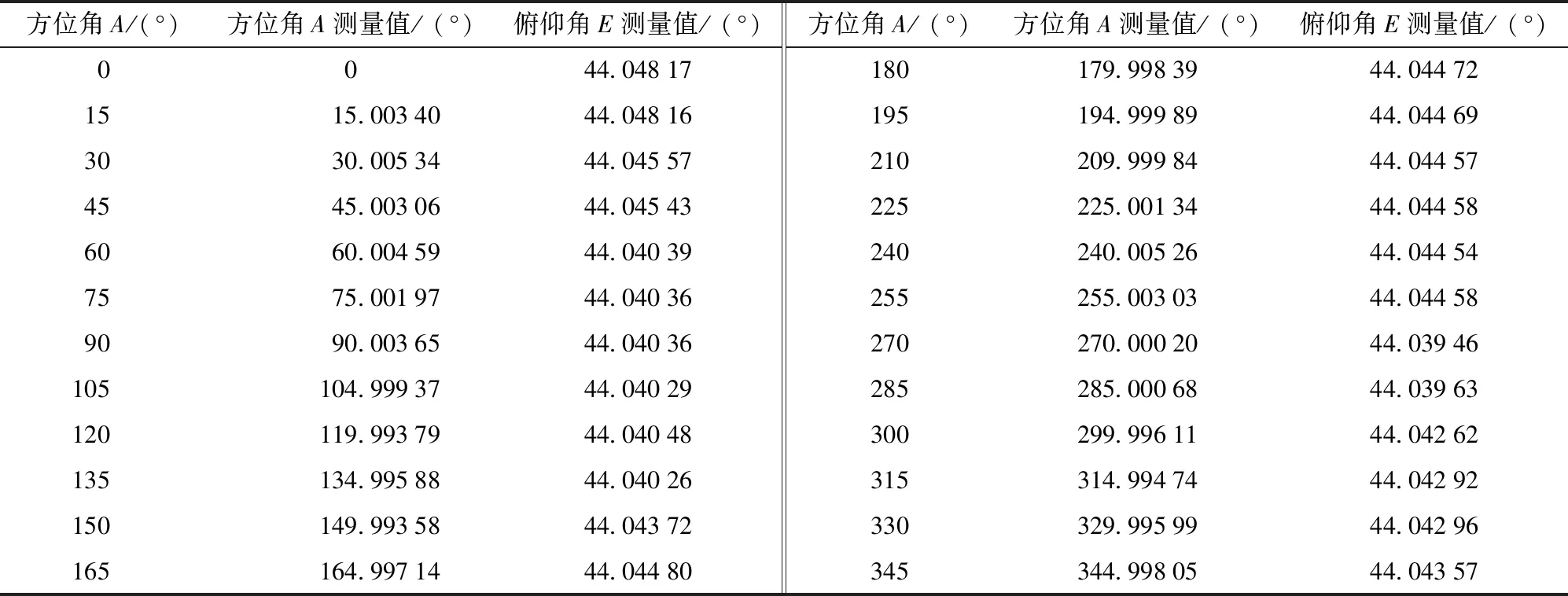
表2 方位角、俯仰角标定值

3.2 误差模型参数辨识

以工控机上设定值作为真值，以全站仪测量值减去设定值所得差值作为指向误差，如图5(a)、图5(c)所示。下面对误差模型参数进行辨识[12-15]。

将方位角误差模型((5)式中的第1个公式)表示为矩阵形式(6)式：

(6)

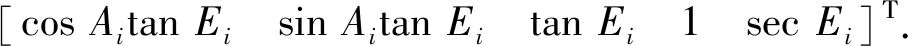
利用最小二乘法曲面拟合(6)式，解出辨识向量xAi，即求解:

(7)

(8)

由图5(c)可知，俯仰角误差是关于A和E的二元函数，俯仰角误差模型式((5)式中的第2个公式)为一元函数，因此在不失模型意义前提下，将俯仰角误差模型式中关于俯仰角E的成分项分离、凑项后(位移x也为E的函数，篇幅有限文中未解释x和E的关系)，俯仰角误差模型式改写为二元函数(9)式：

(9)

将(9)式表示为矩阵形式：

(10)

同理，利用最小二乘法的曲面拟合公式(10)式，可以解出辨识向量xAi和xEi：

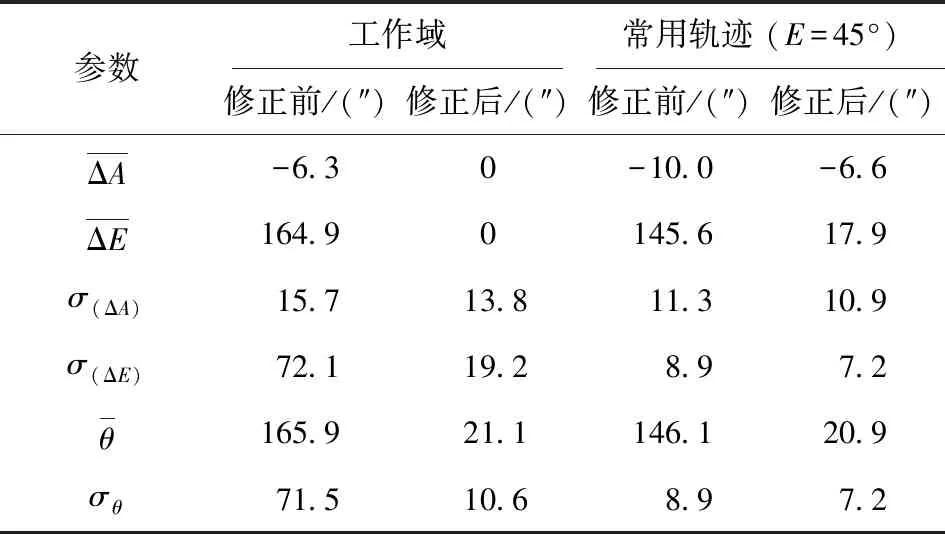
表3 修正前后检测靶标指向精度

3.3 修正效果验证

用误差模型对常用轨迹E=45°、A=(0°，15°，30°，…，345°)处指向误差进行修正，用于验证修正模型的有效性。该轨迹上检测靶标指向误差修正前后结果如图7所示，结果的统计参数列于3.2节如表3所示。

4 结论

本文找出了与检测靶标指向误差相关的23项主要角性误差源与直线位移误差源，根据误差源作用机理和齐次坐标变换原理构建了检测靶标机构的静态空间指向误差模型；在全工作域内384个点处标定了方位误差与俯仰误差，最终由这两个方向误差合成指向误差。虽然标定出的指向误差可以满足设计指标要求，但指向误差富余度较小，为此根据指向误差模型和标定数据，利用曲面拟合方法建立了指向误差修正模型，并对其进行了修正。主要得出以下结论：

1) 由方位角误差与俯仰角误差数学模型可知，引起指向误差的原因是角性误差源，与直线位移误差无关。

2) 由标定的数据样本分析可知，标定出指向误差最大值约为275″，满足设计指标±5′要求；检测靶标在方位方向的指向精度远高于俯仰方向指向精度，即检测靶标机构在装配过程中对引起俯仰误差的各项误差源控制不太理想。

3) 经指向误差修正模型修正后，检测靶标机构在标定点和特定轨道处的总指向误差均值分别为21.1″和20.9″、均方根分别为10.6″和7.2″，与修正前误差数据相比，静态指向误差精度得到了较大提升。

4) 由修正后的残差数量级和规律性可知，修正模型能够剔除检测靶标机构的主要系统误差，但仍含有小量系统误差和随机误差，主要原因是辨识模型参数时将各函数误差当作常量处理，若需要进一步提高精度则可以选择谐波函数消差法[16-18]。