基于声干涉特征匹配的水中目标运动分析研究
徐国军, 张林, 韩梅, 范培勤
(1.海军潜艇学院 二系, 山东 青岛 266199; 2.青岛海洋科学与技术试点国家实验室, 山东 青岛 266237)
0 引言
水中运动目标被动定位一直是水声工作者的重点研究内容。以简正波理论表达海洋波导特别是浅海波导声场时,不同号简正波相互干涉,使低频声场具有稳定的干涉结构,将这种干涉特性引入水中运动目标的被动定位,已成为近20年来水声学的热点研究方向。
浅海声强谱在距离- 频率平面上会呈现明暗相间的干涉条纹。条纹斜率、目标距离及频率的关系可用波导不变量β来表征[1]。β最早由俄罗斯学者Chuprov提出,之后关于β的计算方法[2-4]及其在声学定位方向的应用研究不断发展[5-12]。如文献[5]利用双水平线列阵获取的目标辐射噪声谱干涉结构,建立了一种水中目标距离估计方法;文献[6]利用垂直线列阵,通过声场干涉条纹构造了一种基于虚拟引导声源的水中目标定位方法。文献[9]基于波导不变理论,建立了一种基于扩展卡尔曼滤波的动目标距离连续估计方法。上述算法主要基于固定位置的线列阵或单水听器获取的目标噪声时间- 频率(对应于距离- 频率)谱图,通过谱图条纹结构构建相关算法实现目标距离估计。但在实际工程应用中,特别是对于水下机动观测平台,利用声场干涉结构实现水中目标的运动分析研究还未见报道,更多的见于纯方位目标运动分析(TMA)及其改进方法[13-15],该类算法普遍存在解算时间较长、平台机动要求高等特点。
文献[16-17]基于运动目标的距离时变特性,提出了距离特征量,构建了基于时间- 频率谱图干涉条纹的距离特征量提取方法,通过距离特征量实时反映目标距离的变化情况。文献[17-19]针对舰船目标辐射噪声时间- 频率谱图建立了适用于低信噪比、不连续条纹下的目标距离特征量提取方法;文献[20]利用方位信息、通过构造距离特征量和目标方位的关系模型,给出了一种估计浅海距离特征量的补充方法,理论上分析了水中运动目标方位信息与距离特征量之间的联系。上述有关距离特征量的理论分析建立了目标距离的变化与声场干涉条纹之间的联系,为距离特征量的进一步应用提供了理论支撑。
为改善机动观测平台的水中目标运动分析问题,本文在前述距离特征量研究基础上,联合两方位- 两距离目标运动分析,基于循环匹配寻优处理,建立一种距离特征量匹配分析的目标运动要素估计方法。首先从理论上分析浅海声场干涉条纹现象的成因,介绍干涉条纹信息建立距离特征量估计方法;然后建立以目标初距、瞬距为循环因子,融合两方位- 两距离目标运动参数的计算方法,获取关于距离特征量的匹配代价因子,将每次循环过程中计算的代价因子,分别在对应目标距离、目标航向和目标速度估计结果图中可视化显示,从而实现目标运动要素估计;进一步,对基于距离特征量信息的目标运动分析展开可观测性分析。最后利用仿真和海试数据对算法进行验证。
1 波导不变性及距离特征量
1.1 浅海声场波导不变性
根据浅海声场简正波表达式,频谱为A(ω)、深度为zs的点源发出角频率为ω的声信号,当接收器深度为zr、距声源水平距离为r时,用简正波表示的声压为
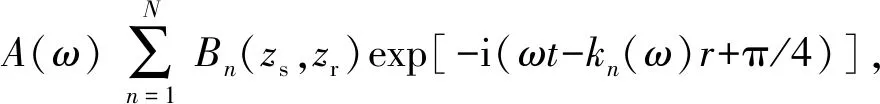
(1)
式中:n为简正波序号,由于截止频率的存在,N与ω的取值有关,ω=2πf,f为声信号频率;Bn(zs,zr)=(2π/[kn(ω)r])1/2Ψn(zs)Ψn(zr),kn(ω)为水平波数,Ψn(z)为第n号简正波的垂向分布函数;t为声信号传播时间;i为虚数单位。
结合(1)式,有声强为
(2)
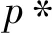
(2)式等号右端相加的两项中,第1项是非相干项、第2项是相干项,相干项由两号简正波两两干涉相互叠加而成,如果每两号简正波干涉形成的条纹斜率互不相同,则多号简正波形成的干涉平面必然杂乱无章。然而通常在浅海波导传播的声场中,任意两号简正波形成的干涉条纹往往具有相同的斜率,如图1中的干涉条纹。Chuprov[1]根据条纹的斜率定义了波导不变量β:
(3)
对于距离- 频率谱图平面上的干涉条纹,可认为其声强处处相等,满足条纹上不同点的声强变化dI=0,即:
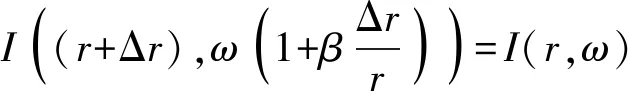
因此可知距离- 频率谱图中(r,ω)处的声强与(r+Δr,ω+ωβΔr/r)处的声强大小一致,其中Δr为距离变化量;或者距离- 频率谱图中角频率ω2处r距离上的声强与角频率ω1处r(ω1/ω2)1/β距离上的声强大小一致。
根据文献[12]对声场简正波的分类,如果声场强度主要由海面反射- 海底反射简正波贡献,则声场干涉条纹对应的波导不变量近似为1. 因此对于典型浅海环境,此时波导不变量可近似为1[8],若某一确定条纹上的两点为(r1,f1)、(r2,f2),则有如下等式成立:

(4)
式中:r1、r2表示目标距离;f1、f2表示目标辐射信号频率。
如图1所示为声强时间- 频率谱图。由图1可见,各亮条纹近似有相同的强度谱。
1.2 距离特征量
文献[16-20]提出了距离特征量,并依托声场干涉结构推导了距离特征量计算方法。所谓距离特征量是指在目标声源与接收器相对运动过程中,t0时刻目标声源与接收器之间的距离与t时刻目标距离的比值,它描述了目标初距与瞬时距离的比值R,反映了目标距离的变化率。如果t0时刻目标距离为D0、t1时刻目标距离为D1,则t0时刻相对t1时刻的距离特征量为
(5)
利用文献[16]提出的基于距离- 频率谱图的多频段距离特征量提取方法,可实时获取目标距离特征量,构造简化距离- 频率谱如图2所示。图2中:横向为距离r、纵向为频率f,图中距离范围为(r1,r2),频率范围为(f1,f2). 以条纹AB为例,其两端分别延长至O(0,0)点和C点,假定B(r3,f3)为该条纹上能量最强的点,F为B点在距离r1方向的投影,D为C点在距离r1方向的投影,H、G分别为A、D点在距离0方向的投影;角度φ为条纹AB与AD的夹角。
结合三角关系,利用(4)式所示距离- 频率关系,可推导距离r1相对距离r2的距离特征量为
(6)
式中:df为时频图中频率轴各采样点的间距;MDC为时频谱图距离范围即DC段对应的采样点数;MBF为线段BF的采样点数;f3=f1+MEF×df,MEF为时频图中最强点相对起始频率在频率轴上的点数,即线段EF对应的点数。
综上所述可知,在实际的目标运动分析过程中,可利用实时获取的目标辐射噪声时间- 频率谱图干涉条纹,实现各时刻距离特征量的实时获取。
2 距离特征量匹配的目标运动要素估计
2.1 两方位- 两距离的目标运动分析方法
以真北线为y轴建立直角坐标系,如图3所示。在t1时刻观测平台位于P1点,目标位于T1点,测得方位F1、距离D1;经时间间隔t12,即在t2时刻观测平台位于P2点,目标位于T2点,测得方位F2、距离D2;Ht为目标航向角;两次测量时间间隔内观测平台横向位移量为x12、纵向位移量为y12,则
(7)
式中:vt为目标速度。
为了便于解算,将三角函数方程变为线性方程,为此设目标速度的横向分量vtx=vtsinHt,目标速度的纵向分量vty=vtcosHt. 则有
(8)
(9)
由此可知,目标速度vt=[(vtx)2+(vty)2]1/2,目标航向Ht=sign(vtx)arcos(vty/vt).
在已知Ht、vt和D1的基础上,即可按(10)式求出任意时刻的目标距离Di:

(10)
式中:t1i为第i时刻相对初始时刻的时间差。设中间变量A=D1sinF1+vtxt1i-x1i,B=D1cosF1+vtyt1i-y1i,则目标方位Fi为
(11)
距离特征量Ri为
(12)
2.2 距离特征量匹配代价因子
依据2.1节的方法计算各时刻距离特征量值,结合匹配思想构建距离特征量匹配代价因子,实现目标运动要素估计。具体构建步骤如下:
步骤1根据目标可能的距离范围[Dmin,Dmax],设定目标初距D0和目标瞬距Da的距离区间,确定距离区间最小步长间隔Δd.
步骤2构造初距D0j、当前时刻瞬距Dak两层循环(j,k),j=1,…,J;k=1,…,K,J、K分别为选取的目标初距区间和目标瞬距区间采样数。
步骤3利用已知的初始时刻目标方位F0、当前时刻目标方位Fi、声呐平台运动参数(航向、航速或各时刻位置信息),选定的目标初距D0j、计算时刻目标瞬距Dak,结合前文两方位-两距离目标参数计算方法,估计各时刻目标瞬距信息{ati}.
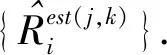
步骤5利用实测目标辐射噪声获取其时间-频率谱图,根据前文所述距离特征量计算方法,得到各时刻距离特征量{Ri,i=0,…,N}.
步骤6构造代价因子:
(13)
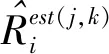
2.3 可测性分析
分析距离特征量匹配模型实现过程不难发现,该模型的本质是利用时间- 频率谱图呈现出的干涉条纹信息、目标方位信息、平台与目标位置几何关系信息,基于匹配思想实现目标运动参数估计。模型可观测性可等效于目标方位Fi、Ri两观测量已知条件下目标运动分析过程的可观测性问题。
假定目标做匀速直线运动,目标与观测平台的相对位置关系如图4所示,初始时刻观测平台位于坐标原点。目标初始位置T0、速度vt、航向Ht,相对观测平台初始方位F0、初始距离D0;ti时刻目标运动到Ti(xti,yti)点,观测平台运动到Pi(xpi,ypi)点,目标瞬时距离Di、相对观测平台方位为Fi、方位变化量βi=Fi-F0.
当取目标初距D0、目标x轴方向速度vtx为状态量时,运动方程形式如下:
(14)
ati+bηi=xpi,
(15)
则可得观测方程组为
(16)
利用最小二乘方法,构造如下观测方程组:
(17)
式中:N为观测次数。显然,模型可观测条件为观测矩阵G的逆矩阵存在,即矩阵G的行列式不等于0. 有矩阵G的行列式为
(18)
式中:h为观测时刻。将变量ηi=-sinβi/Ri代入(18)式,进一步得到观测矩阵行列式:
tith(vtxti-xpi)(vtxth-xph).
(19)
分析(19)式,可得到如下不可观测条件:
1) 当观测平台静止,即xpi=xph=…=0时,观测矩阵行列式|G|=0,系统不可观测;
2) 当目标与观测平台在同一直线运动时,βi=0,即(18)式中ηi=0,行列式|G|=0,系统不可观测;
3) 当观测平台与目标均保持匀速直线运动时,系统不可观测,此结论可证明如下:
令观测平台以速度vp匀速直线运动,此时x轴方向速度分量为vpx,有
xpi=ti×vpx,
(20)
此时观测矩阵行列式为
tith(vtxti-xpi)(vtxth-xph)=
tith(vtx-vpx)(vtx-vpx)tith=0,
(21)
即观测矩阵行列式为0,系统不可观测。证毕。
显然,系统可观测(即状态向量有解)的一个必要条件是观测平台必须机动,即在观测过程中观测平台至少进行一次变向处理或变速处理(变速机动时目标与平台不在同一直线)。
3 数值验证
3.1 数值仿真
假定初始时刻运动声源距离观测平台7 km、位于平台方位0°,声源以航向180°、速度8 m/s匀速直线运动;在解算过程中,前120 s观测平台速度2 m/s、航向10°,120 s开始速度变为3 m/s、逐渐转向至280°. 基于Kraken简正波模型,利用各时刻声源距离仿真得到的声强时频谱如图1所示。利用2.1节计算方法可在该仿真态势条件下获取声源目标距离特征量(见图5),结合距离特征量信息,利用2.2节目标运动分析过程得到500 s时估计的声源初距、速度和航向可视化结果图(见图6),可估计目标运动要素分别为38.3 cab(7 100 m)、15.55 kn(8.0 m/s)和180.15°. 对比声源各运动要素真值不难发现,该方法在500 s时估计的运动要素最大误差仅1.4%,表明将距离特征量信息引入水中目标运动分析能够取得较好的目标运动要素估计结果。
目标辐射噪声在海洋中传播时,由于受到海洋环境影响,接收信号信噪比会存在不同程度的降低,即其时间- 频率谱图干涉条纹将出现模糊或断续的现象,由此获取的距离特征量会相应存在误差,文献[18-19]对此进行了详细介绍,并提出了提高距离特征量精度的提取方法。为分析距离特征量对算法估计的影响,表1给出了距离特征量取不同的随机误差、在不同时长条件下估计的目标运动要素估计结果,包含估计的具体数值及对应的估计误差,具体可视化结果如图7~图15所示。
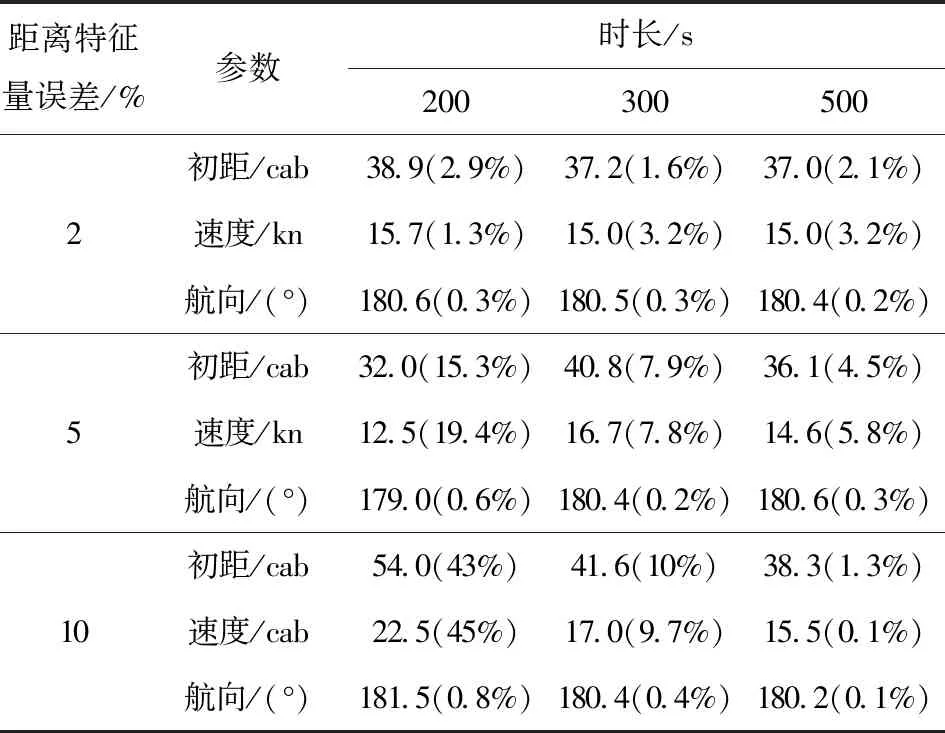
表1 距离特征量不同误差时目标运动要素估计值与误差
分析表1中的数据可知,当距离特征量误差小于5%时,计算时长300 s即可获得较准确的目标运动要素估计结果;当距离特征量误差小于10%时,计算时长500 s可获得准确的目标运动要素结果。随着距离特征量误差的增大,可视化图中目标要素峰值主瓣越宽,峰值越不明显,估计结果稳定性变弱。根据文献[16-20]的分析,对于实际海上活动中稳定跟踪的目标,其辐射噪声时间- 频率谱图提取的距离特征量误差一般小于5%.
图16、图17所示为当前仿真态势条件下,目标方位误差方差分别为0.3°和0.5°时目标运动分析(TMA)算法估计结果。由图16和图17可知,当目标要素解算收敛误差小于10%时,解算时长分别为530 s和610 s左右,随着方位误差的增大,目标要素解算收敛用时增加。
分析以上仿真结果不难得出如下结论:基于距离特征量匹配寻优处理的目标运动分析方法,由于仅利用起始时刻和计算时刻两个时间点的目标方位信息,可忽略方位误差对算法的影响;对于距离特征量误差在5%时,仍然能够在300 s左右获得较准确的目标要素估计,相比TMA算法在解算时长、精度上有较大改善。
3.2 试验数据分析
选取某专项试验获取的数据对算法进行验证。以航次A为例,试验过程中目标船以航向350°、速度15 kn(约7.72 m/s)匀速直航,解算开始时刻目标距离声呐平台46 cab(约8.5 km),目标方位182°. 图18给出了A航次观测平台航向和航速信息。
试验过程目标声源辐射噪声获取的时间- 频率谱如图19所示。谱图处理得到目标方位及距离特征量信息如图20所示。基于距离特征量匹配处理的目标运动分析过程,在解算400 s时估计获得的目标初距、速度和航向三要素可视化结果如图21所示。给出的目标运动三要素结果分别为:目标初距为48.5 cab、速度为16.5 kn、航向为354°,误差最大为目标速度估计结果约10%.
图22~图25所示为航次B中目标与声呐平台相互态势信息、观测平台接收目标辐射噪声时间- 频率谱图、估计的目标方位及距离特征量信息以及解算400 s时新算法获取的可视化结果图,其中目标初距、目标速度和目标航向真值分别为50.8 cab、15 kn和340°,算法估计结果分别为50 cab、14 kn和337°,目标各要素估计最大误差为速度估计结果(误差6.7%)。
分析2.2节算法的实现过程不难发现,该匹配方法由于仅利用到初始时刻和计算时刻两个时间点的目标方位值,相比于传统纯方位目标运动分析,可有效规避目标方位观测误差的影响,更适应水中机动平台的水声目标运动分析问题。
以上仿真结果与试验数据结果分析均表明,基于距离特征量匹配处理的目标运动分析方法,可通过处理目标辐射噪声获取的时间- 频率谱图获得实时的目标距离特征量结果,结合目标初距、瞬距两层循环寻优处理,利用本文构建的匹配代价因子可快速、准确估计目标运动三要素。
4 结论
本文以海洋声场干涉结构特征为基础,利用运动目标辐射噪声时间- 频率谱图干涉条纹获取目标距离特征量,将距离特征量信息引入目标运动分析过程,构建了基于实测距离特征量与目标运动分析估计距离特征量之间的匹配最优代价因子,基于匹配给出的可视化结果图,实现目标运动三要素的估计。利用仿真和海试数据对算法进行了验证,取得较好的实验结果。得到主要结论如下:
1) 本文方法仅利用两个时刻的目标方位信息,不需要实时量测目标方位,可有效规避存在于TMA算法中方位量测误差对算法估计结果的影响。
2) 基于距离特征量匹配实现目标运动要素估计方法,能够快速给出目标运动要素估计可视化结果图,获取的目标运动要素估计在时效性、准确性上相比TMA算法有较大改善。
3) 本文提出的基于声干涉特征匹配的目标运动分析方法,适应于水下机动平台的目标要素解算,易于工程实现,具有广阔的应用前景。

