基于混合禁忌搜索算法的分时电价下并行机调度优化

吴宇娟

（安徽工业大学管理科学与工程学院，马鞍山243032）

0 引言

全球经济的发展导致了能源消耗的增加，能源短缺成为许多国家经济发展的瓶颈。国际能源署（International Energy Agency，IEA）2015 年发布的研究报告指出，2040 年全球的能源需求总量将比2015 年增长37%[1]。在产生和消耗能源的过程中，大量温室气体被排放到大气中，给环境造成了严重污染[2]。作为最大的制造业国家，我国正面临着能源节约和环境保护的严峻挑战，采取充分考虑节能的生产决策显得尤为重要。

电能作为二次能源广泛应用于生产生活中，同时也是大部分制造业使用的主要能源[3-4]。但电能很难存储，用电方在不同的时段对电力的需求不同[5]。为了使电力供需达到平衡，供电方往往会采取分时电价（Time of Use，ToU）机制来引导用电方降低高峰时期用电需求从而降低高峰时期电网负荷[6]。分时电价机制是指根据电网负荷和用电需求将一天分为多个时段，对于不同的时段采取不同的定价方案。分时电价的实施不仅可以提高电网系统的稳定性，同时也可促使用电方将高峰时段的加工任务调整到用电平段及低谷时段，进而减少电力消耗总成本[7-8]。

为了更好地适应分时电价机制，生产管理者需要通过调度来调整他们的生产任务。调度是指将有限的资源分配到不同的任务中，以此来优化一个或者多个目标的决策过程[9]。其中，单机调度是一类基本的调度问题，相关研究可以为解决并行机调度问题提供参考。Zhang 等人[10]研究了分时电价下最小化总用电成本的单机调度问题，构建了混合整数线性规划（MILP）模型并设计了带有多级过滤机制的贪婪插入算法来进行求解。

相同并行机调度不仅是单机调度问题的泛化，而且是流水车间调度的一个特例[9],在制造过程中应用广泛，是学者们的研究热点。曹江北等[11]研究了最小化加工周期相同并行机的工件排序问题，并提出了一个基于蚂蚁系统的算法。Su[12]研究了带有工件交货期及机器能力约束的相同并行机调度问题，目标为最小化最大完工时间，采用启发式算法及分支定界算法进行求解。Xu 等人[13]研究了以最小化加权完成时间和最大完工时间总和为目标的相同并行机调度问题，构建了一个混合整数规划模型并采用带有Dantzig-Wolfe 分解的列生成方法来进行求解。

现有的相同并行机调度问题基本上都是以时间相关的标准作为优化目标，如最小拖期量，最大完工时间。然而，随着绿色制造的深入实践，考虑能耗的并行机调度问题逐渐成为研究热点，尤其是，分时电价机制作为有效调节能耗的一种方法，已被广泛应用[14-15]。因此，如何结合分时电价机制，优化相同并行机总用电成本的调度问题，对制造业的节能减排具有重要意义。

1 问题描述与模型建立

考虑一组工件N={1,2,…,n}需要在M={1,2，…,m}台相同并行机上进行加工。其中，工件i ∈N 在所有机器上的加工时间为ti，单位电耗率为pi，每台机器在同一时刻最多只能加工一个工件，每个工件只能选择在一台机器上进行加工，加工过程中不允许中断。所有的工件都在零时刻到达，所有的机器在零时刻都是可用的，不考虑机器的故障和预防性维护。

分时电价机制下，不同时段对应的电价是不同的。本文将一整天分为K 个时段,每个时段k ∈K 都有其对应的电价ck及开始时间bk。时段k 的时间间隔可由[bk,bk+1]表示，时段 k 的持续时间表示为Tk(Tk=bk+1-bk)。为了便于求解，设置b1=0，同时bK+1不小于加工所有工件的最大完工时间，以保证该问题始终会存在可行解。

本文所研究的问题是要在给定的时间范围内，将每一个工件分配到合适的机器上同时确定其加工位置，使得加工所有工件的总用电成本最小。每个工件可能在一个或多个时段内加工，这就需要确定每个工件在所有时段内实际的加工时间，基于对问题的分析，定义以下决策变量：

xijk:工件i 在机器 j 的时段 k 内的加工时间

根据以上的符号以及定义，建立如下的混合整数线性规划（MILP）模型：

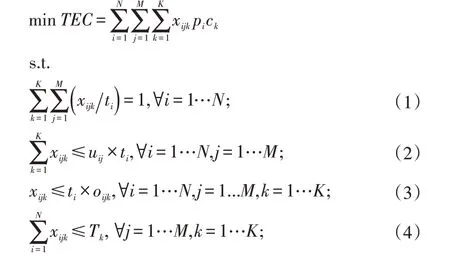
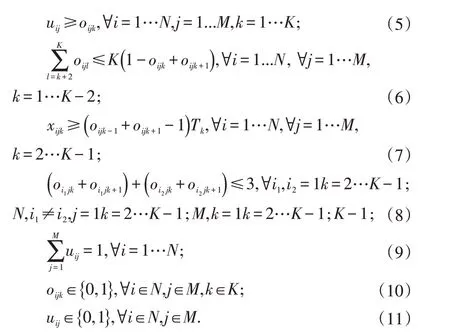
模型优化目标为最小化加工所有工件的总用电成本。式（1）确保每一工件分配到所有机器各个时段的加工时间之和应当等于工件的加工时长。式（2）表示如果工件i 在机器j 上加工（即uij=1），那么这个工件在该机器上的所有时段内的加工时间之和不能超过其实际的加工时间。式（3）指如果工件i 不在机器j 的时段k 内加工（即oijk=1），那么工件i 在机器j 的时段k 内的加工时间为0。式（4）表示在某台机器的某个时段内所有工件的加工时间之和不超过这个时段的持续时间。

式（5）表示的是两个0-1 变量之间的包含关系，如果oijk=1,那么uij=1 必然成立。式（6-8）表示任一工件都以不可中断的方式被加工。式（9）是确保每一个工件只能在一台机器上进行加工。式（10-11）是决策变量的二元约束。Zhang 等人[12]证明其研究的分时电价下单机调度问题是NP-hard 问题，本文在其研究基础上增加了一个机器选择的问题，因此，本文所研究的问题同样是NP-hard 问题。此外，可知在本文构建的连续时间混合整数线性规划模型中，变量的数目为2NMK+NM，约束的数目为O(N2Mk)+O(MNK2)。

2 禁忌搜索-多级过滤贪婪插入启发式算法

并行机调度问题一般可以分为两个子问题，第一个子问题是将工件分配到机器上，第二个子问题是在每台机器上调度已经分配的工件。当第一个子问题解决之后，第二个子问题变为每台机器上的单机调度问题。对于工件机器分配这个子问题，本文利用负载平衡原则进行处理，而对于每台机器上的工件调度，采取多级过滤贪婪插入启发式算法来进行求解。

基于负载平衡原则的工件机器分配方法如下：对每台机器，计算出已分配到该机器的所有工件的加工时间总和，待分配工件选择总加工时间最小的那台作为加工机器，然后更新加工机器的总加工时间，迭代循环，直到所有工件分配完成。通过这个规则，不仅可以将工件分配到机器上，同时可以计算出加工这些工件所需要的总时间，确定加工时间下界。

首先所有工件按其加工电耗率从大到小排序得到一个初始序列，通过负载平衡原则将序列中的工件分配到机器上，接着采取多级过滤贪婪插入启发式计算出所有机器的总用电成本。由于每个工件在每台机器上的加工时间及电耗率都是相同的，其加工次序决定了工件所分配的机器及最终加工位置。即工件的加工序列决定了解的质量，因此，为了得到理想解，本文利用禁忌搜索算法对初始序列进行迭代优化，选出使总电成本最小的加工序列。

2.1 多级过滤贪婪插入启发式算法

（1）基于负荷均衡的工件分配

在该阶段，算法在于实现以机器负荷均衡为原则将工件分配到相应的机器上，而Davis 和Jaffe[16]设计的列表调度（List Scheduling，LS）启发式算法可以有效地实施这个分配规则。主要步骤包括：首先，所有工件按照其电耗率从大到小进行排序，然后，工件按照列表的顺序分配给具有最小总加工时间的第一台可用机器。最后，更新机器的总加工时间，并重复上述步骤，直到分配完所有工件。具体流程如算法1 所示，算法中涉及的相关定义如下：

定义1机器j 的总加工时间用TPj表示，指已分配到机器j 上的所有工件的加工时间之和。设Sj表示在机器j 上加工的工件集，

设l 表示工件的加工顺序列表。tij，pij分别表示工件i 在机器j(1 ≤j ≤M)上的加工时间及电耗率，且其值可提前确定。同时，变量 Pj，用来储存机器j(1 ≤j ≤M)上已分配的工件。

算法1列表调度启发式

1.设TPj≔0,for 1 ≤j ≤M,

2.设l 表示工件的加工顺序列表，

//初始解的l 是工件按其电耗率从大到小排序得来的，之后的l 是通过对初始的l 变换得到。

3.for i=1 to N do

4.end for

5.输出Pj,for 1 ≤j ≤M。

（2）基于贪婪插入启发式的工件调度

在第一阶段完成之后，所有工件已经分配到了相应的机器上，此时，问题变为如何对每一机器上已分配的工件进行调度优化，即分时电价下的单机调度问题。为解决该问题，本文提出了一个带有多级过滤的贪婪插入启发式算法，以此最小化加工所有工件的电耗总成本。

该算法的思想是将调度过程分为粗粒度过滤以及细粒度过滤两个阶段，在调度之前，所有插入位置按照电价分为低、中、高三个层次,记为layer1、layer2、layer3。在粗粒度阶段，工件首先按照电耗率从大到小排序，然后将每个工件依次分配到不同的电价层次；在细粒度阶段，分析每个工件所在的电价层次、加工时间、电耗率、时段电价来确定最终工件的插入位置。具体流程如算法2 所示。

算法2带有多级过滤机制的贪婪插入启发式算法

1.设Tcost ≔0,

2.for j=1 to M do

2.1.设 l*≔ Pj,

2.2.将 l*中工件按电耗率从大到小排序，得到新的排序列表lj，

2.3.设 ，

2.4.for i=1 to N do

a.if i ∈layer1 do

a.1.工件i 选择layer1层插入成本最低的位置，计算出电成本cost1,

a.2.计算cost ≔cost+cost1,

a.3.工件i 插入到这个位置并更新机器上layer1层的所有工件的插入位置layoutj,

b.elseif i ∈layer2 do

b.1.工件i 选择layer2层插入成本最低的位置，计算出电成本cost2,

b.2.计算cost ≔cost+cost2,

b.3.工件 i 插入到这个位置并更新机器上layer2层的所有工件的插入位置layoutj,

c.elseif i ∈layer3 do

c.1.工件i 选择layer3层插入成本最低的位置，计算出电成本cost3,

c.2.计算cost ≔cost+cos t3,

c.3.工件 i 插入到这个位置并更新机器上layer3层的所有工件的插入位置layoutj,

d.endif

2.5.end for

2.6.Tcost ≔Tcost+cost,

3.end for

4.输出Tcost,layoutjfor 1 ≤j ≤M。

2.2 算法总体框架

基于以上分析，算法的整体流程如算法3 所示。

算法3禁忌搜索-多级过滤贪婪插入启发式算法

1.所有工件按其电耗率从大到小排序,记为l，

2.由算法1 确定每台机器上的加工工件，

3.由算法2 计算所有工件的总用电成本及加工位置,记为X,并设置禁忌表为空，

4.判断是否满足终止条件，若是，便结束算法并输出优化结果；否则，继续以下步骤，

5.利用X、l、算法1 以及算法2 计算产生若干个邻域解，并从中选择若干个候选解，

6.判断候选解是否满足藐视准则，若是，跳转到步骤8，若不是，继续以下步骤，

7.判断候选解对应的各对象的禁忌属性，选出新的当前解，更新禁忌表，

8.转到步骤4。

3 实验结果分析

为了验证本文所构建的MILP 模型和禁忌搜索-多级过滤贪婪插入启发式算法的有效性，本部分将随机生成一组算例来对比模型以及算法求解的质量。算法是在MATLAB 2018a 中编码，MILP 模型由AMPL（版本3.1.0）的CPLEX 求解器求解。具体实验环境为:3.60 GHz 的Intel Core i7-4790 CPU、16 GB 内存、Windows 7 64 位操作系统个人计算机。

实验的所有测试都采用中国安徽省执行的ToU 方案，如表1 所示。该ToU 定价方案将一天分为六个时段，其中包含三种类型的电价：高峰期、中高峰期、低谷期，并假设第一天上午8 点作为时间范围的零点。

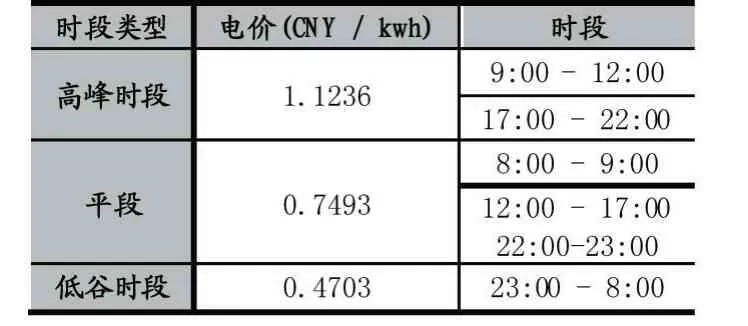
表1 实验采用的分时电价方案

在产生随机案例时，每个工件在机器上的电耗率遵循[30,100]Kw 之间的均匀分布，每个工件的加工时间同样服从[30,210]min 的均匀分布。在这组实验中，工件数设置为N=30,50,70,90,100，机器数设置为M=5,10,20。CPLEX 求解器的时间设置为3600s，如果在该时间点内无法获得最佳目标值，则输出当前解。算法中禁忌搜索算法的相关参数由算例规模确定，由于初始解的结果较好，本文采用固定禁忌长度15，终止步数50 进行实验。每组实验结果均为10 次随机实验计算的平均值，实验天数由加工时间下界确定，机器数为5，工件数为60-100 时天数设为2，其他规模的算例天数均为1。GMT=(TECT-TECM)/TECM×100%，用来评估模型和算法的解的质量，其中TECT表示算法求出的最优解，TECM表示模型求出的最优解。

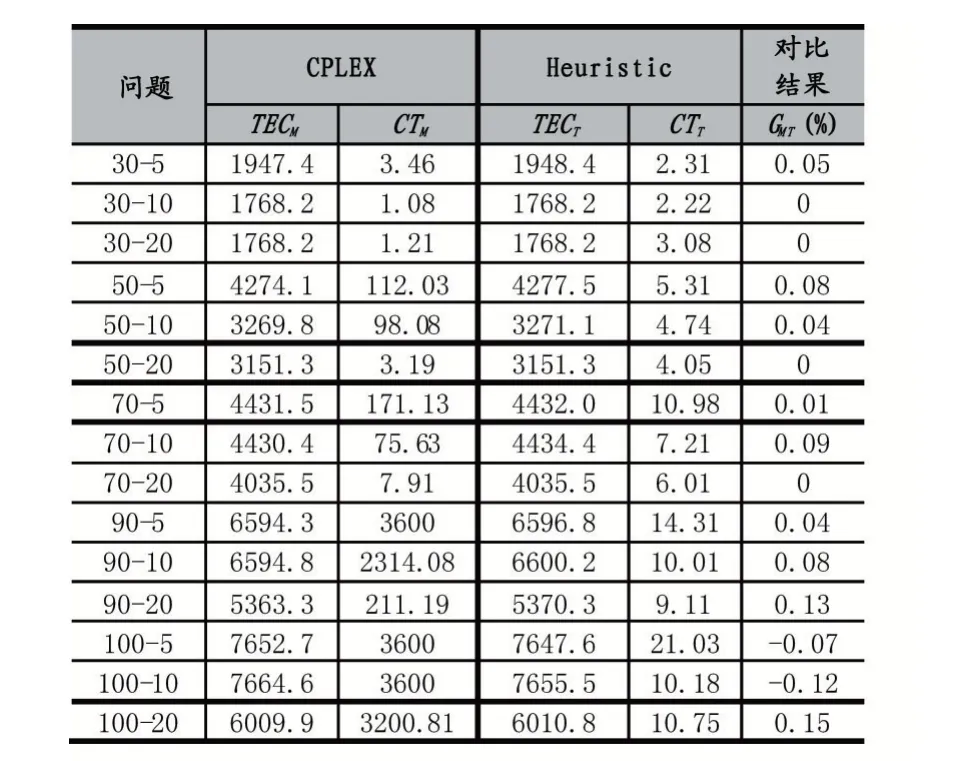
表2 模型与算法的实验对比

由表2 可知，本文所构建的算法和CPLEX 求解器计算的目标值之间的差距不超过0.15%，计算结果非常相近，而算法的计算时间总体上要比CPLEX 的计算时间短，尤其是当工件数超过70，差距更加明显。同时，从表2 可以发现，当工件数不超过90 时，CPLEX 求得的解要优于算法求得的解，并且工件数越少，CPLEX计算时间的变化越平稳。当工件数达到100，加工机器数为5 和10 时，CPLEX 求得的解比算法求得的解要差。此时，CPLEX 在3600s 内不能输出最优解，而算法在10.18s 及21.03s 时就输出了求得的最优解，不仅解的质量较好，而且求解的时间非常短。综上所述，本文构建的模型以及算法都是可行且有效的，模型适合求解小规模问题，而算法更加适合解决大规模问题。

4 结语

针对分时电价下相同并行机调度问题，本文构建了一个以总用电成本最小化为目标的连续时间的MILP 模型，模型中采用工件在时段内的加工时间作为决策变量，解决了离散模型造成大量0-1 变量的问题，进而降低了模型的复杂度。同时，针对分时电价下相同并行机调度模型的特点，本文提出了一种有效的禁忌搜索-多级过滤贪婪插入启发式算法。算法采用负载平衡原则进行工件机器分配，大大降低了计算的难度。实验结果证明了该方法的在求解质量及求解速度方面的有效性。

后续研究中，将会进一步探讨如何将本文构建的算法用于分时电价下多工序多阶段的工件调度问题，并尝试将本文构建的MILP 模型及算法扩展到其他调度环境，如柔性作业车间和混合流水车间。