数字正弦波发生器设计实验案例分析与探讨

徐望明

（武汉科技大学信息科学与工程学院，武汉430081）

0 引言

在通信技术、电子技术、仪器仪表和工业控制等领域的信号处理系统中，会经常使用到正弦波信号、三角波信号、方波信号等信号源。随着数字器件如单片机、DSP（Digital Signal Processor）技术的发展，已有多种数字化方法可用于产生应用所需的信号源[1-2]。其中，数字正弦波发生器是《单片机原理与应用》、《DSP 原理与应用》等课程实验教学中的一个典型实验项目，要求学生在规定的实验课时内设计一个数字信号发生器，产生指定参数（如频率、幅度等）的正弦波信号。

通常所用的方法是查表法和泰勒级数展开法[3]。前者输出响应快，但精度依赖于存储空间，一般只适用于对精度要求不高的场合；后者所占存储单元少，但精度依赖于展开项数，项数越多则精度越高，但相应运算量会越大、效率越低，实用性不强。

本文以数字正弦波发生器设计实验为案例，介绍一种运算速度快、精度高而且使用的存储空间少的方法——差分方程迭代法来产生正弦序列，灵活且实用。本文结合数学中的三角函数公式推导了产生正弦序列的差分方程，继而紧密结合专业基础理论知识，从信号与系统分析的角度推导出了相同差分方程，并进一步探讨了以产生的正弦波为基础，通过函数转换的方法来产生三角波、方波等波形的方法，以及可通过一定参数设置来实现输出波形幅度和频率可调的方法。

1 产生正弦序列的差分方程迭代法

1.1 从数学分析的角度进行推导

在信号处理系统中，如果想要产生输出精度可调的正弦波，可使用差分方程迭代法[4]，其基本原理为建立产生正弦序列的差分方程，这样就可从给定的初始值推导出后面的正弦序列。差分方程的一种推导方法是利用数学中的三角函数公式：

令α=nω,β=(n-2)ω，则：

记y(n)=sin nω，则:当n=0 时，y(0)=0；当n=1时，y(1)=sin ω；当n ≥2 时，y(n)=2 cos ω y( n-1)-y( n-2)，即为差分方程：

其中A=2 cos ω,B=-1。

设希望输出频率为fd的正弦信号sin(2πfdt)，用数字器件（如单片机、DSP 等）来实现，实际得到的是一个正弦序列，可认为是sin(2πfdt)经大小为fs的采样频率采样后而得到，即sin(2πfdnT)，其中n 为自然数为采样周期。令则采样后的正弦序列为sin(nω)。

若fd=0.4kHz，fs=16kHz，则差分方程系数为：A=2×0.98768834，B=-1，且 初 始 值y(0)=0,y(1)=0.15643447。

根据差分方程迭代法原理不难编写出C 语言程序，实现生成指定参数的正弦波信号。

1.2 从信号与系统分析的角度进行推导

上面的原理推到基于纯数学公式，结合专业基础理论知识，也可从信号与系统分析的角度推导出差分方程，与专业紧密联系，更易于理解。

把输出正弦序列看做系统的单位冲激响应序列，即h(n)=sin(nω)。对该序列作Z 变换得：

其中a=2 cos(ω),b=-1,c=sin(ω)。

对式（1）求逆Z 变换得差分方程[2]：

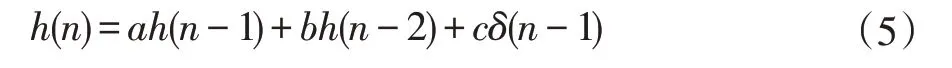
根据实际设计指标，可计算出系数a、b、c。当fd=0.4kHz，fs=16kHz，则a=1.97537668，b=-1，c=0.15643447。

可见，数字正弦信号发生器可表示为一个二阶离散系统，h(n)=sin(nω)为其单位序列响应。由初始状态为零，即h(-1)=0，h(-2)=0，由式（5）易得：h(0)=0，h(1)=c=sin(ω)，当n≥2 时：

该差分方程实际上与式（3）所示的差分方程是一样的。

2 从正弦波发生器到多功能波形发生器

正弦波的前半个周期的正弦波值都是大于零（在横坐标轴以上），而正弦波的后半个周期的正弦波值都是小于零（在横坐标轴以下），利用此特点，三角波、方波等波形也都可用函数变换的方法生成。

（1）将正弦波前半个周期（即波形值大于零的部分）用线性函数（N 为一周期的采样点数）来转换，可实现了在原前半个周期正弦波的基础上成功输出三角波前半个周期的波形；将正弦波后半个周期（即波形值小于零的部分）用线性函数来转换，可实现了在原后半个周期正弦波的基础上成功输出三角波后半个周期的波形，由此实现了三角波的输出。

（2）方波在一个周期内，其波形值只有两种取值，例如上半周期取1，下半周期取-1 或0。基于此特点，很容易在正弦的基础上产生所需的方波信号，具体做法是：对正弦信号设定一个判决门限，大于此门限取一个值，小于此门限取另外一个值。以幅度为1 和0 的方波信号为例，只需将正弦波前半个周期波形值大于零的部分（判决门限为0）用函数Y=1 来转换；将正弦波后半个周期（即波形值小于零的部分）用函数Y=0 来转换，从而实现了占空比为50%的方波信号产生。

3 实现波形幅度和频率可调的方法

对于以上各种波形，为了实现输出幅度可调，在程序中设置幅度参数即可。

为了实现输出波形的频率可调，先来看采样率和波形频率之间的关系为：

其中：fs为采样率，N 为一周期的采样点数，m 为步长，fd为波形频率。

可见，通过适当改变步长m、改变一周期的采样点数N 或可通过定时器设置改变采样率fs来改变输出波形的频率，从而达到实现输出波形的频率可调性。

4 结语

以数字正弦波发生器设计实验为案例，本文利用差分方程迭代法给出了一种快速、灵活且实用的实现方案，从纯数学分析的角度和信号与系统分析的角度分别进行了差分方程的推导，得到了一致的结果，进而以正弦波发生器为基础，探讨了产生三角波、方波等波形的方法，以及如何实现波形幅度和频率可调。